第1单元 圆 (预习衔接.培优卷.含解析)-2025-2026学年六年级上册数学北师大版
文档属性
| 名称 | 第1单元 圆 (预习衔接.培优卷.含解析)-2025-2026学年六年级上册数学北师大版 |  | |
| 格式 | doc | ||
| 文件大小 | 126.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 23:04:26 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
预习衔接.培优卷 第1单元 圆
一.选择题(共3小题)
1.如图,该图的一半,再一半,结果是( )
A. B. C.
2.世界上第一个把圆周率的值计算精确到七位小数的人是( )
A.华罗庚 B.张衡 C.祖冲之 D.陶行知
3.关于圆,下列说法中,正确的是( )
①圆有无数条对称轴,半圆只有一条对称轴。
②圆上每一点到圆心的距离都相等。
③圆是曲线图形。
④一个圆两条不同的直径相交的点一定是圆心。
A.②③④ B.①② C.①②③ D.①②③④
二.填空题(共3小题)
4.如图中, 是圆心角。
5.一个周长是12.56厘米的圆,它的周长和直径的比值叫做 ,这个圆的直径是 厘米。
6.看图填一填。
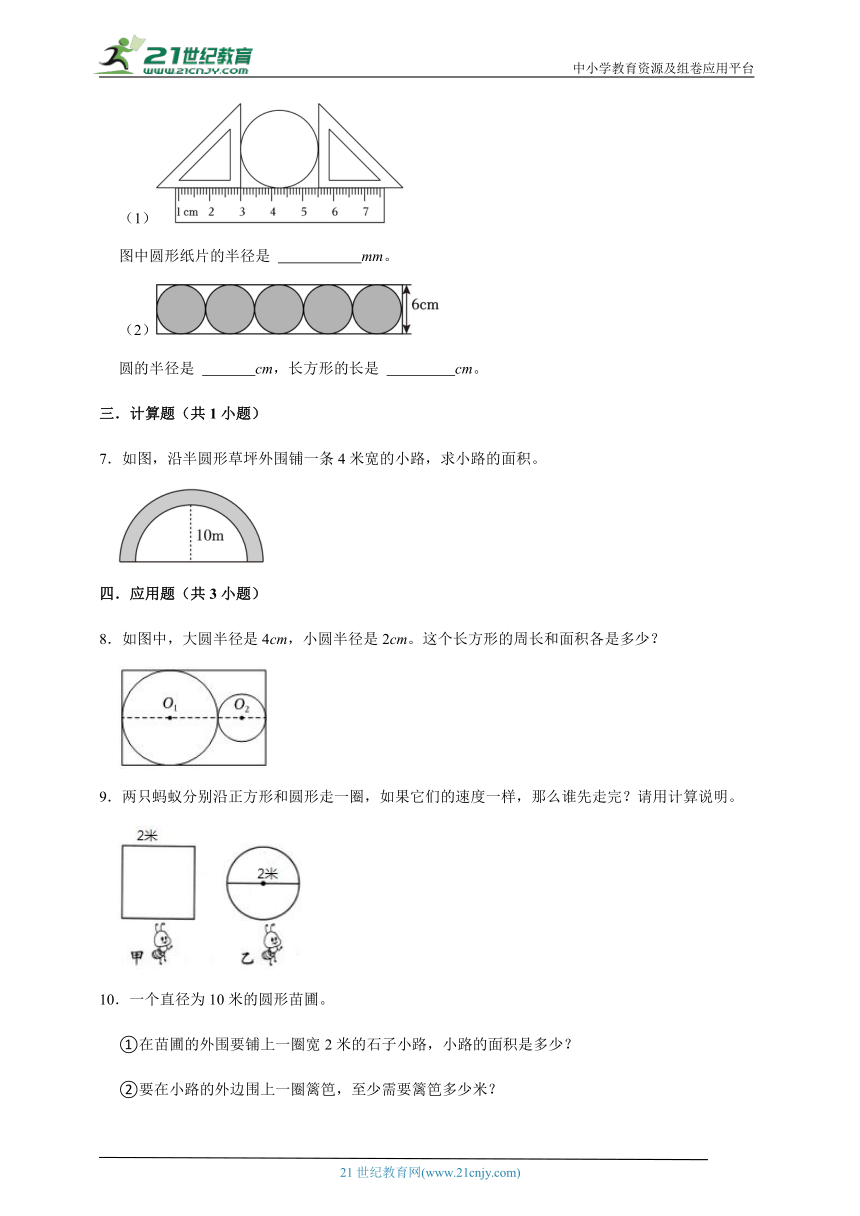
(1)
图中圆形纸片的半径是 mm。
(2)
圆的半径是 cm,长方形的长是 cm。
三.计算题(共1小题)
7.如图,沿半圆形草坪外围铺一条4米宽的小路,求小路的面积。
四.应用题(共3小题)
8.如图中,大圆半径是4cm,小圆半径是2cm。这个长方形的周长和面积各是多少?
9.两只蚂蚁分别沿正方形和圆形走一圈,如果它们的速度一样,那么谁先走完?请用计算说明。
10.一个直径为10米的圆形苗圃。
①在苗圃的外围要铺上一圈宽2米的石子小路,小路的面积是多少?
②要在小路的外边围上一圈篱笆,至少需要篱笆多少米?
预习衔接.培优卷 第1单元 圆
参考答案与试题解析
一.选择题(共3小题)
1.如图,该图的一半,再一半,结果是( )
A. B. C.
【考点】圆的认识与圆周率;分数的意义和读写.
【专题】平面图形的认识与计算.
【答案】C
【分析】将这个圆当作单位“1”,根据分数的意义可知,它的一半是原来的,所以它的一半的一半是原为的×=.
【解答】解:×=;
故选:C。
【点评】完成本题的依据是分数的意义,即将单位“1”平均分成若干份,表示这样一份或几份的数为分数.
2.世界上第一个把圆周率的值计算精确到七位小数的人是( )
A.华罗庚 B.张衡 C.祖冲之 D.陶行知
【考点】圆的认识与圆周率.
【答案】C
【分析】根据课本上“你知道吗”介绍的关于圆周率的相关内容选出即可.
【解答】解:祖冲之(公元429﹣500年).他研究圆周率,得出其值就在3.1415926与3.1415927之间,准确到小数点后7位,成为世界上第一个把圆周率的值精确到七位小数的人.
故选:C。
【点评】此题考查关于圆周率的历史,培养学生民族自豪感.
3.关于圆,下列说法中,正确的是( )
①圆有无数条对称轴,半圆只有一条对称轴。
②圆上每一点到圆心的距离都相等。
③圆是曲线图形。
④一个圆两条不同的直径相交的点一定是圆心。
A.②③④ B.①② C.①②③ D.①②③④
【考点】圆的认识与圆周率.
【专题】平面图形的认识与计算;几何直观.
【答案】D
【分析】①圆和半圆都是轴对称图形,如图所示:圆有无数条对称轴,半圆只有1条对称轴;
②圆上点到圆心的距离是圆的半径,圆有无数条长度相等的半径,即圆上每一点到圆心的距离都相等;
③根据圆的定义,平面上一动点以一定点为中心,一定长为距离运动一周的轨迹称为圆周,简称圆,所以圆是曲线图形;
④圆有无数条长度相等的直径,直径都经过圆心,则一个圆两条不同的直径相交的点一定是圆心。
【解答】解:由分析可知:正确的有①②③④。
故选:D。
【点评】本题考查了圆的特征。
二.填空题(共3小题)
4.如图中, ∠COD 是圆心角。
【考点】圆的认识与圆周率.
【专题】平面图形的认识与计算;几何直观.
【答案】∠COD。
【分析】顶点在圆心,两条边都在圆上的角叫做圆心角。
【解答】解:∠COD是圆心角。
故答案为:∠COD。
【点评】本题考查了圆心角的认识。
5.一个周长是12.56厘米的圆,它的周长和直径的比值叫做 圆周率 ,这个圆的直径是 4 厘米。
【考点】圆的认识与圆周率.
【专题】平面图形的认识与计算;几何直观.
【答案】圆周率,4。
【分析】根据圆周率的含义:圆的周长和它直径的比值,叫做圆周率,圆的周长公式是C=πd,利用周长除以π即可求出直径。
【解答】解:12.56÷3.14=4(厘米)
答:一个周长是12.56厘米的圆,它的周长和直径的比值叫做圆周率,这个圆的直径是4厘米。
故答案为:圆周率,4。
【点评】本题考查了圆的周长公式及圆周率的认识。
6.看图填一填。
(1)
图中圆形纸片的半径是 12.5 mm。
(2)
圆的半径是 3 cm,长方形的长是 30 cm。
【考点】圆的认识与圆周率.
【专题】平面图形的认识与计算;空间观念.
【答案】(1)12.5;(2)3,30。
【分析】(1)圆的直径是(5.5﹣3)cm,同一个圆内,半径是直径的,据此计算换算单位即可;
(2)一个圆的直径是6cm,半径是直径的,长方形的长是由5个直径组成,据此计算解答。
【解答】解:(1)5.5﹣3=2.5(cm)
2.5÷2=1.25(cm)
1.25cm=12.5(mm)
因此图中圆形纸片的半径是12.5mm。
(2)6÷2=3(cm)
6×5=30(cm)
答:圆的半径是3cm,长方形的长是30cm。
故答案为:12.5;3,30。
【点评】本题考查了同一个圆内半径与直径的关系应用。
三.计算题(共1小题)
7.如图,沿半圆形草坪外围铺一条4米宽的小路,求小路的面积。
【考点】圆、圆环的面积.
【专题】几何直观;应用意识.
【答案】150.72平方米。
【分析】通过观察图形可知,小路的面积是半环形面积,根据环形面积公式:S=π(R2﹣r2),把数据代入公式解答。
【解答】解:10+4=14(米)
3.14×(142﹣102)÷2
=3.14×(196﹣100)÷2
=3.14×96÷2
=150.72(平方米)
答:小路的面积是150.72平方米。
【点评】此题主要考查环形面积公式的灵活运用,关键是熟记公式。
四.应用题(共3小题)
8.如图中,大圆半径是4cm,小圆半径是2cm。这个长方形的周长和面积各是多少?
【考点】圆、圆环的面积;圆、圆环的周长.
【专题】几何直观;应用意识.
【答案】40厘米,96平方厘米。
【分析】通过观察图形可知,这个长方形的等于大小圆的直径和,宽等于大圆的直径,根据长方形的周长公式:C=(a+b)×2,面积公式:S=ab,把数据代入公式解答。
【解答】解:(4+2+2×2+4×2)×2
=(8+4+8)×2
=20×2
=40(厘米)
(4×2+2×2)×(4×2)
=(8+4)×8
=12×8
=96(平方厘米)
答:这个长方形的周长是40厘米,面积是96平方厘米。
【点评】此题主要考查长方形的周长公式、面积公式的灵活运用,关键是熟记公式。
9.两只蚂蚁分别沿正方形和圆形走一圈,如果它们的速度一样,那么谁先走完?请用计算说明。
【考点】圆、圆环的周长;正方形的周长.
【专题】几何直观;应用意识.
【答案】乙先走完。
【分析】根据正方形的周长公式:C=4a,圆的周长公式:C=πr2,把数据代入公式求出正方形、圆的周长,然后进行比较即可。
【解答】解:2×4=8(米)
3.14×2=6.28(米)
6.28<8
答:乙先走完。
【点评】此题主要考查正方形、圆的周长公式的灵活运用,关键是熟记公式。
10.一个直径为10米的圆形苗圃。
①在苗圃的外围要铺上一圈宽2米的石子小路,小路的面积是多少?
②要在小路的外边围上一圈篱笆,至少需要篱笆多少米?
【考点】圆、圆环的面积;圆、圆环的周长.
【专题】平面图形的认识与计算;几何直观;应用意识.
【答案】①75.36;
②43.96。
【分析】①根据环形面积公式:S=π(R2﹣r2),把数据代入公式解答。
②根据圆的周长公式:C=πd,把数据代入公式解答。
【解答】解:①10÷2=5(米)
5+2=7(米)
3.14×(72﹣52)
=3.14×(49﹣25)
=3.14×24
=75.36(平方米)
答:小路的面积是75.36平方米。
②10+2+2=14(米)
3.14×14=43.96(米)
答:至少需要篱笆43.06米。
【点评】此题主要考查环形面积公式、圆的周长公式的灵活运用,关键是熟记公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.培优卷 第1单元 圆
一.选择题(共3小题)
1.如图,该图的一半,再一半,结果是( )
A. B. C.
2.世界上第一个把圆周率的值计算精确到七位小数的人是( )
A.华罗庚 B.张衡 C.祖冲之 D.陶行知
3.关于圆,下列说法中,正确的是( )
①圆有无数条对称轴,半圆只有一条对称轴。
②圆上每一点到圆心的距离都相等。
③圆是曲线图形。
④一个圆两条不同的直径相交的点一定是圆心。
A.②③④ B.①② C.①②③ D.①②③④
二.填空题(共3小题)
4.如图中, 是圆心角。
5.一个周长是12.56厘米的圆,它的周长和直径的比值叫做 ,这个圆的直径是 厘米。
6.看图填一填。
(1)
图中圆形纸片的半径是 mm。
(2)
圆的半径是 cm,长方形的长是 cm。
三.计算题(共1小题)
7.如图,沿半圆形草坪外围铺一条4米宽的小路,求小路的面积。
四.应用题(共3小题)
8.如图中,大圆半径是4cm,小圆半径是2cm。这个长方形的周长和面积各是多少?
9.两只蚂蚁分别沿正方形和圆形走一圈,如果它们的速度一样,那么谁先走完?请用计算说明。
10.一个直径为10米的圆形苗圃。
①在苗圃的外围要铺上一圈宽2米的石子小路,小路的面积是多少?
②要在小路的外边围上一圈篱笆,至少需要篱笆多少米?
预习衔接.培优卷 第1单元 圆
参考答案与试题解析
一.选择题(共3小题)
1.如图,该图的一半,再一半,结果是( )
A. B. C.
【考点】圆的认识与圆周率;分数的意义和读写.
【专题】平面图形的认识与计算.
【答案】C
【分析】将这个圆当作单位“1”,根据分数的意义可知,它的一半是原来的,所以它的一半的一半是原为的×=.
【解答】解:×=;
故选:C。
【点评】完成本题的依据是分数的意义,即将单位“1”平均分成若干份,表示这样一份或几份的数为分数.
2.世界上第一个把圆周率的值计算精确到七位小数的人是( )
A.华罗庚 B.张衡 C.祖冲之 D.陶行知
【考点】圆的认识与圆周率.
【答案】C
【分析】根据课本上“你知道吗”介绍的关于圆周率的相关内容选出即可.
【解答】解:祖冲之(公元429﹣500年).他研究圆周率,得出其值就在3.1415926与3.1415927之间,准确到小数点后7位,成为世界上第一个把圆周率的值精确到七位小数的人.
故选:C。
【点评】此题考查关于圆周率的历史,培养学生民族自豪感.
3.关于圆,下列说法中,正确的是( )
①圆有无数条对称轴,半圆只有一条对称轴。
②圆上每一点到圆心的距离都相等。
③圆是曲线图形。
④一个圆两条不同的直径相交的点一定是圆心。
A.②③④ B.①② C.①②③ D.①②③④
【考点】圆的认识与圆周率.
【专题】平面图形的认识与计算;几何直观.
【答案】D
【分析】①圆和半圆都是轴对称图形,如图所示:圆有无数条对称轴,半圆只有1条对称轴;
②圆上点到圆心的距离是圆的半径,圆有无数条长度相等的半径,即圆上每一点到圆心的距离都相等;
③根据圆的定义,平面上一动点以一定点为中心,一定长为距离运动一周的轨迹称为圆周,简称圆,所以圆是曲线图形;
④圆有无数条长度相等的直径,直径都经过圆心,则一个圆两条不同的直径相交的点一定是圆心。
【解答】解:由分析可知:正确的有①②③④。
故选:D。
【点评】本题考查了圆的特征。
二.填空题(共3小题)
4.如图中, ∠COD 是圆心角。
【考点】圆的认识与圆周率.
【专题】平面图形的认识与计算;几何直观.
【答案】∠COD。
【分析】顶点在圆心,两条边都在圆上的角叫做圆心角。
【解答】解:∠COD是圆心角。
故答案为:∠COD。
【点评】本题考查了圆心角的认识。
5.一个周长是12.56厘米的圆,它的周长和直径的比值叫做 圆周率 ,这个圆的直径是 4 厘米。
【考点】圆的认识与圆周率.
【专题】平面图形的认识与计算;几何直观.
【答案】圆周率,4。
【分析】根据圆周率的含义:圆的周长和它直径的比值,叫做圆周率,圆的周长公式是C=πd,利用周长除以π即可求出直径。
【解答】解:12.56÷3.14=4(厘米)
答:一个周长是12.56厘米的圆,它的周长和直径的比值叫做圆周率,这个圆的直径是4厘米。
故答案为:圆周率,4。
【点评】本题考查了圆的周长公式及圆周率的认识。
6.看图填一填。
(1)
图中圆形纸片的半径是 12.5 mm。
(2)
圆的半径是 3 cm,长方形的长是 30 cm。
【考点】圆的认识与圆周率.
【专题】平面图形的认识与计算;空间观念.
【答案】(1)12.5;(2)3,30。
【分析】(1)圆的直径是(5.5﹣3)cm,同一个圆内,半径是直径的,据此计算换算单位即可;
(2)一个圆的直径是6cm,半径是直径的,长方形的长是由5个直径组成,据此计算解答。
【解答】解:(1)5.5﹣3=2.5(cm)
2.5÷2=1.25(cm)
1.25cm=12.5(mm)
因此图中圆形纸片的半径是12.5mm。
(2)6÷2=3(cm)
6×5=30(cm)
答:圆的半径是3cm,长方形的长是30cm。
故答案为:12.5;3,30。
【点评】本题考查了同一个圆内半径与直径的关系应用。
三.计算题(共1小题)
7.如图,沿半圆形草坪外围铺一条4米宽的小路,求小路的面积。
【考点】圆、圆环的面积.
【专题】几何直观;应用意识.
【答案】150.72平方米。
【分析】通过观察图形可知,小路的面积是半环形面积,根据环形面积公式:S=π(R2﹣r2),把数据代入公式解答。
【解答】解:10+4=14(米)
3.14×(142﹣102)÷2
=3.14×(196﹣100)÷2
=3.14×96÷2
=150.72(平方米)
答:小路的面积是150.72平方米。
【点评】此题主要考查环形面积公式的灵活运用,关键是熟记公式。
四.应用题(共3小题)
8.如图中,大圆半径是4cm,小圆半径是2cm。这个长方形的周长和面积各是多少?
【考点】圆、圆环的面积;圆、圆环的周长.
【专题】几何直观;应用意识.
【答案】40厘米,96平方厘米。
【分析】通过观察图形可知,这个长方形的等于大小圆的直径和,宽等于大圆的直径,根据长方形的周长公式:C=(a+b)×2,面积公式:S=ab,把数据代入公式解答。
【解答】解:(4+2+2×2+4×2)×2
=(8+4+8)×2
=20×2
=40(厘米)
(4×2+2×2)×(4×2)
=(8+4)×8
=12×8
=96(平方厘米)
答:这个长方形的周长是40厘米,面积是96平方厘米。
【点评】此题主要考查长方形的周长公式、面积公式的灵活运用,关键是熟记公式。
9.两只蚂蚁分别沿正方形和圆形走一圈,如果它们的速度一样,那么谁先走完?请用计算说明。
【考点】圆、圆环的周长;正方形的周长.
【专题】几何直观;应用意识.
【答案】乙先走完。
【分析】根据正方形的周长公式:C=4a,圆的周长公式:C=πr2,把数据代入公式求出正方形、圆的周长,然后进行比较即可。
【解答】解:2×4=8(米)
3.14×2=6.28(米)
6.28<8
答:乙先走完。
【点评】此题主要考查正方形、圆的周长公式的灵活运用,关键是熟记公式。
10.一个直径为10米的圆形苗圃。
①在苗圃的外围要铺上一圈宽2米的石子小路,小路的面积是多少?
②要在小路的外边围上一圈篱笆,至少需要篱笆多少米?
【考点】圆、圆环的面积;圆、圆环的周长.
【专题】平面图形的认识与计算;几何直观;应用意识.
【答案】①75.36;
②43.96。
【分析】①根据环形面积公式:S=π(R2﹣r2),把数据代入公式解答。
②根据圆的周长公式:C=πd,把数据代入公式解答。
【解答】解:①10÷2=5(米)
5+2=7(米)
3.14×(72﹣52)
=3.14×(49﹣25)
=3.14×24
=75.36(平方米)
答:小路的面积是75.36平方米。
②10+2+2=14(米)
3.14×14=43.96(米)
答:至少需要篱笆43.06米。
【点评】此题主要考查环形面积公式、圆的周长公式的灵活运用,关键是熟记公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
