2026年中考《数学》复习课件:专题五 四边形-微专题(九) 与四边形有关的综合题(44张PPT)
文档属性
| 名称 | 2026年中考《数学》复习课件:专题五 四边形-微专题(九) 与四边形有关的综合题(44张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 09:13:38 | ||
图片预览









文档简介
(共44张PPT)
复习讲义
第一篇 考点精讲
专题五 四边形
微专题(九) 与四边形有关的综合题
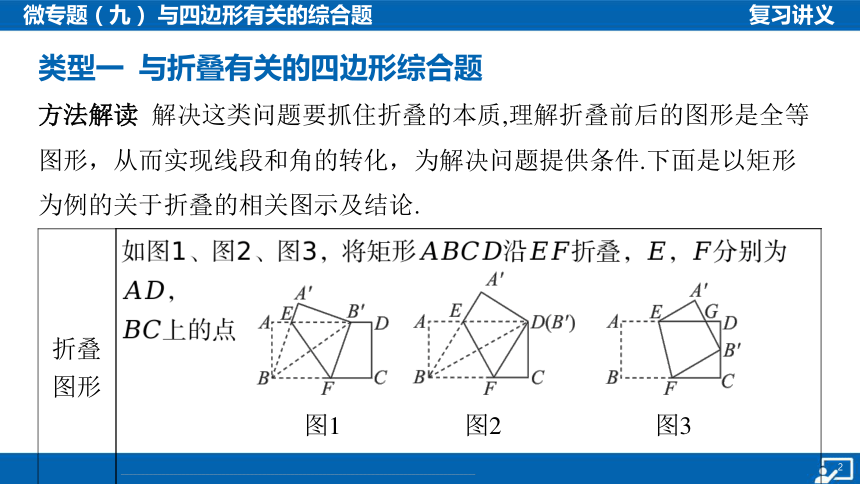
类型一 与折叠有关的四边形综合题
方法解读 解决这类问题要抓住折叠的本质,理解折叠前后的图形是全等
图形,从而实现线段和角的转化,为解决问题提供条件.下面是以矩形
为例的关于折叠的相关图示及结论.
折叠 图形 如图1、图2、图3,将矩形沿折叠,,分别为 ,
上的点
_________________________________________________________________________________________
图1
图2
图3
图形 分析 及相 关结 论 如图1、图2、图3,,
如图1、图2,角平分线()遇平行线 时出现等腰三角形 , 为等腰三角形
如图1、图2,对称点的连线被对称轴垂直平分 折痕 垂直平分,从而可知四边形 为菱形
(图1、图2),(图1、图2),
(图2), (图3)等都是直角三角形,在这些直角三角形中,可利用勾股定理求相关线段的长
续表
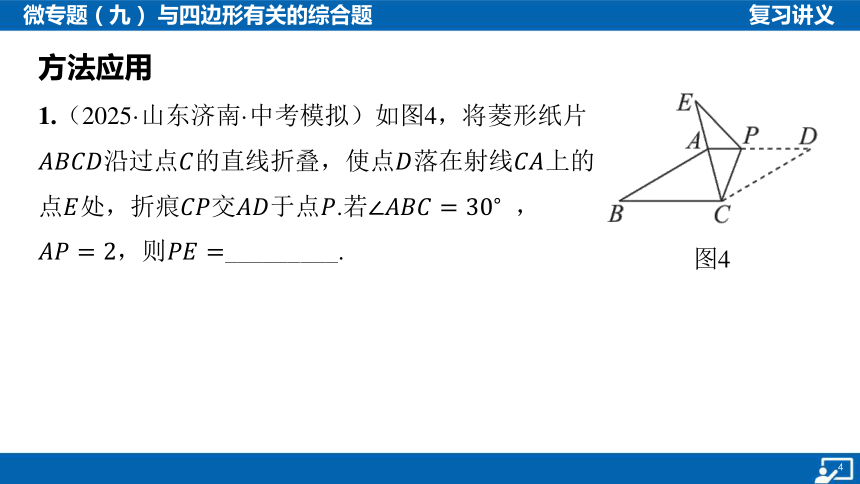
方法应用
图4
1.(2025·山东济南·中考模拟)如图4,将菱形纸片
沿过点的直线折叠,使点落在射线 上的
点处,折痕交于点.若 ,
,则 _________.
提示:过点作于点 .由菱形的性质,得
, .从而得
.由折叠的性质,得
.所以 .
在中, .在
中, .故
.
图4
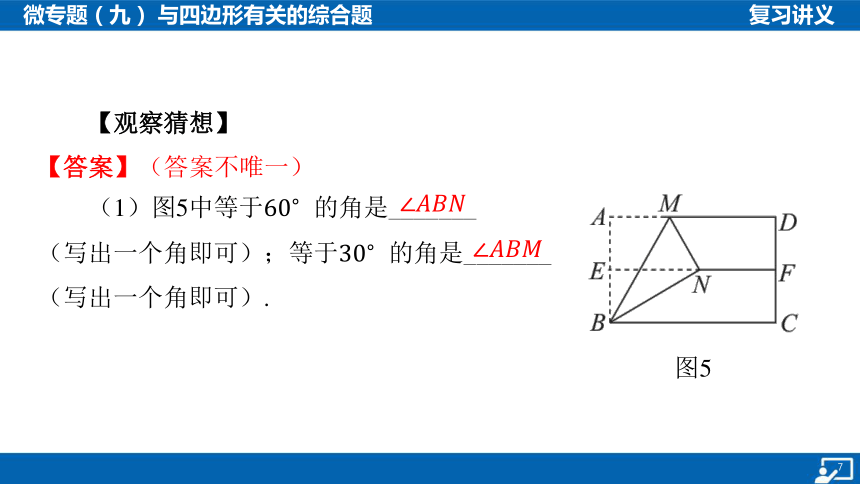
2.教材变式[人教版八下第64页活动一变式]探究与证明
【动手操作】如果我们身旁没有量角器或三角尺,又需要作 ,
, 等大小的角,那么可以采用下面的方法: 如图5,对折矩形
纸片,使与重合,得到折痕 ,把纸片展平;再一次折叠
纸片,使点落在上的点处,折痕为 .
【观察猜想】
【答案】(答案不唯一)
图5
(1)图5中等于 的角是_______
(写出一个角即可);等于 的角是_______
(写出一个角即可).
【推理验证】
(2)请证明(1)中的猜想结论.
图34
证明:如图34,连接 .
由折叠的性质,得,,垂直平分
,即 是等边三角形.
.
∴ .
3.(2025·内蒙古通辽·中考模拟)综合与实践课上,老师让同学们以“正方形
的折叠”为主题开展数学活动,有一名同学操作过程如下:
操作一,对折正方形纸片,使与重合,得到折痕 ,
把纸片展平;
操作二,在上取一点,沿折叠,使点 落在正方形内部的点
处,把纸片展平,连接,,延长交于点,连接 .
(1)如图6,当点在上时,____ .
30
图6
提示:由折叠的性质知,, , . .
图7
(2)改变点在上的位置(点不与点, 重合),如图7,判断与 的数量关系,并说明理由.
解: .
理由:由折叠的性质,得, .
.
四边形是正方形, , . 在 和R中,,,
.
类型二 与旋转有关的四边形综合题
方法解读 解决这类问题时,需仔细观察图形旋转前后相关的线段之间的
数量关系、位置关系,相关的角的变化及角与角之间的关系,从中提炼出
基本图形和常用模型,如当旋转角为 时,通常会形成等腰直角三角形
或正方形,需结合三角形的性质、特殊四边形的判定与性质、全等
(相似)三角形的判定与性质、勾股定理等知识求解.
方法应用
4.如图8,为正方形内一点, ,将绕点 按顺时针方向旋转 ,得到(点,的对应点分别为点, ).延长交于点,连接 .
图8
(1)试判断四边形 的形状,并说明理由.
解:四边形 是正方形.
理由:由旋转的性质,得 , .
,,在同一直线上,∴ .
图8
四边形 是矩形.
由旋转的性质,得
四边形 是正方形.
(2)如图9,已知,请猜想线段与 的数量关系并加以证明.
图9
解:.
理由:过点作 于点,则 , .
∵ ,
四边形 是正方形, , .
∴ .
.
图9
在和中,, ,,∴
.
由旋转的性质,得 .
由(1)得,四边形是正方形.
∴ .
图10
5.(2024·山西·中考节选)综合与探究
【图形呈现】如图10,四边形 为菱形,过点作于
点,过点 作于点 .
【猜想证明】
(1)判断四边形 的形状,并说明理由.
解:四边形为矩形.
理由: ,, , .
四边形为菱形, , .
∴ 四边形 为矩形.
【深入探究】
图11
(2)将图11中的绕点 逆时针旋转,
得到,点,的对应点分别为, .如图
11,当线段经过点时, 所在直线分别与
线段,交于点,.猜想线段与 的
数量关系,并说明理由.
图11
解:.
理由: 四边形 为菱形, , .
由旋转的性质,得,
, .
在和中, ,,,∴
,即 .
类型三 与动点有关的四边形综合题
方法解读 解决这类问题的基本策略是“化动为静”,要抓住图形中的等
量关系和各个元素的变化情况,要特别注意一些不变的量、不变的关系
或特殊关系,将其化动为静,由特殊情形(特殊点、特殊值、特殊位置、
特殊图形等)逐步过渡到一般情形,即选取动点运动路径中的任意一个
位置形成静态图形,再由静态图形的性质得出题设中变量间的关系.
方法应用
图12
6.(2024·山东威海·中考节选)如图12,在菱形
中,, , 为对角
线上的动点,以为边作 ,
交射线于点,连接,.点从点 出发,
沿方向以每秒的速度运动至点 处停止.设
的面积为,点的运动时间为 .
图12
(1)求证: .
证明:设与相交于点
四边形 为菱形, ,, .
在和中,, , ,
, .
,∴ .
又 ,
.
(2)求与的函数解析式,并写出自变量 的取值范围.
图12
解:过点作于点,则 .
,
四边形 为菱形, , , ,即 .
,∴ ,
∴ .
∴
∵ , .
微专题练习(九) 与四边形有关的综合题
类型一 与折叠有关的四边形综合题
图1
1.(2025·四川攀枝花·模拟)如图1,将矩形沿 折叠,
使点落在边上的点处,过点作交于点 ,
连接.给出以下结论:;②四边形 是菱
形;;④当,时, 的长
为 .其中正确的是________.(填序号)
图46
提示:由,得 .由折叠的性质,
得,, .从而得
.所以 .故①正确.由此可得,
,所以四边形 是菱形.故
②正确.如图46,连接,交于点 .由菱形的性质,
得,.由 ,
,得.所以,即 .由
此可得,.故③错误.如图46,过点
作于点,则四边形 是矩形,
.由,得 ,
即.解得或
(舍去).因为, ,所以
. 由, ,
得.从而得.所以, 即
.所以 .由此可得,
.故④正确.
图46
2.(2024·山东潍坊·中考)如图2,在矩形中,,点 ,
分别在边,上.将沿折叠,点的对应点 恰好落在对角
线上;将沿折叠,点的对应点恰好也落在对角线 上.
连接, .
图2
图2
(1)求证: .
证明: 四边形是矩形, , , //
.
由折叠的性质,得, ,, .
, .
.
在和 中,, ,,
.
(2)求证:四边形 为平行四边形.
图2
解:由(1)知 ,, ,
四边形 为平行四边形.
类型二 与旋转有关的四边形综合题
图3
3.(2024·吉林·中考)如图3,在平面直角坐标系
中,点的坐标为,点的坐标为 .以
,为边作矩形.若将矩形绕点
顺时针旋转 ,得到矩形,则点 的坐
标为( ).
C
A. B. C. D.
4.(2024·海南·中考)如图4,菱形的边长为2, ,
边在数轴上,将绕点顺时针旋转,点落在数轴上的点 处.若点
表示的数是3,则点 表示的数是( ).
图4
A.1 B. C.0 D.
图4
【答案】D
提示:过点C作的垂线,垂足为点 .由菱形的性质,得,平分 ,.所以 . 从而得 .所以.因为 ,所以 .由此可得,.所以. 所以 .又点表示的数是3,故点A表示的数是 .
5.(2025·湖南衡阳·中考改编)
【问题探究】
(1)如图5(见下页),在正方形中,对角线,相交于点 .
在线段上任取一点(端点除外),连接, .
图5
①将线段绕点逆时针旋转,使点落在的延长线上的点处.当点 在线段上的位置发生变化时, 的大小是否发生变化?请说明理由.
图5
解:的大小不发生变化, .
理由:如图47,过点作, ,垂足分别为点,
四边形是正方形, , .
, .
在和 中,,,
, ,
即 .
②探究与 的数量关系,并说明理由.
图5
图47
解:.
理由:如图47,过点 作交于点,垂足为点,过点 作于点,垂足为点
四边形 是正方形, , , 垂直平分
,四边形 是矩形,
,
,
图47
, ,
, ,
.
【迁移探究】
(2)如图6,将正方形换成菱形,且 ,其他条件不变.试探究与 的数量关系,并说明理由.
图6
解:.
理由: 四边形 是菱形, , , ,
是等边三角形, 垂直平分
,
,∴ .
图48
如图48,过点作交于点 ,过点作交于点,则四边形 是平行四边形, , , ,,都是等边三角形.
.
过点作 于点,则,,
.
类型三 与动点有关的四边形综合题
图7
6.(2024·广东·中考)如图7,菱形 的面积为
24,是的中点,是上的动点.若 的面积
为4,则图中阴影部分的面积为____.
小锦囊 观察图形可发现,
.连接 ,
由是的中点,易得.连接,通过分析 的
面积和的面积的数量关系来得到与 的数量关系,从而计算
出 的面积.
图7
提示:连接,.因为是 的中点,所以
.同理可得
.因为 ,所以
.所以 .所以
.故
.
答案:10
7.(2025·甘肃庆阳·模拟)探究与证明
【图形呈现】
图8
(1)如图8,四边形是正方形,是对角线 上
一点.求证: .
证明:(方法一) 四边形 是正方形, , .
在和中,, ,,
.
(方法二)连接 交于点, 四边形是正方形, ,,即 垂直平分 .
【深入探究】
图9
(2)如图9,在正方形中,是对角线 上一
点,,,垂足分别为点, ,连接
,猜想与 的数量关系,并证明你的猜想.
猜想: .
证明:由(1)可知,
,, .
四边形是矩形.
.
【拓展应用】
(3)如图10,在正方形中,,是对角线 上一点,过点
作于点,于点.则 的最小值为_____.
图10
提示:如图49,连接, 四边形是正方形,
,,.由勾股定理,得 .同
(2)可得,四边形是矩形,则.当时, 最小,
最小值为.故的最小值为 .
图49
复习讲义
第一篇 考点精讲
专题五 四边形
微专题(九) 与四边形有关的综合题
类型一 与折叠有关的四边形综合题
方法解读 解决这类问题要抓住折叠的本质,理解折叠前后的图形是全等
图形,从而实现线段和角的转化,为解决问题提供条件.下面是以矩形
为例的关于折叠的相关图示及结论.
折叠 图形 如图1、图2、图3,将矩形沿折叠,,分别为 ,
上的点
_________________________________________________________________________________________
图1
图2
图3
图形 分析 及相 关结 论 如图1、图2、图3,,
如图1、图2,角平分线()遇平行线 时出现等腰三角形 , 为等腰三角形
如图1、图2,对称点的连线被对称轴垂直平分 折痕 垂直平分,从而可知四边形 为菱形
(图1、图2),(图1、图2),
(图2), (图3)等都是直角三角形,在这些直角三角形中,可利用勾股定理求相关线段的长
续表
方法应用
图4
1.(2025·山东济南·中考模拟)如图4,将菱形纸片
沿过点的直线折叠,使点落在射线 上的
点处,折痕交于点.若 ,
,则 _________.
提示:过点作于点 .由菱形的性质,得
, .从而得
.由折叠的性质,得
.所以 .
在中, .在
中, .故
.
图4
2.教材变式[人教版八下第64页活动一变式]探究与证明
【动手操作】如果我们身旁没有量角器或三角尺,又需要作 ,
, 等大小的角,那么可以采用下面的方法: 如图5,对折矩形
纸片,使与重合,得到折痕 ,把纸片展平;再一次折叠
纸片,使点落在上的点处,折痕为 .
【观察猜想】
【答案】(答案不唯一)
图5
(1)图5中等于 的角是_______
(写出一个角即可);等于 的角是_______
(写出一个角即可).
【推理验证】
(2)请证明(1)中的猜想结论.
图34
证明:如图34,连接 .
由折叠的性质,得,,垂直平分
,即 是等边三角形.
.
∴ .
3.(2025·内蒙古通辽·中考模拟)综合与实践课上,老师让同学们以“正方形
的折叠”为主题开展数学活动,有一名同学操作过程如下:
操作一,对折正方形纸片,使与重合,得到折痕 ,
把纸片展平;
操作二,在上取一点,沿折叠,使点 落在正方形内部的点
处,把纸片展平,连接,,延长交于点,连接 .
(1)如图6,当点在上时,____ .
30
图6
提示:由折叠的性质知,, , . .
图7
(2)改变点在上的位置(点不与点, 重合),如图7,判断与 的数量关系,并说明理由.
解: .
理由:由折叠的性质,得, .
.
四边形是正方形, , . 在 和R中,,,
.
类型二 与旋转有关的四边形综合题
方法解读 解决这类问题时,需仔细观察图形旋转前后相关的线段之间的
数量关系、位置关系,相关的角的变化及角与角之间的关系,从中提炼出
基本图形和常用模型,如当旋转角为 时,通常会形成等腰直角三角形
或正方形,需结合三角形的性质、特殊四边形的判定与性质、全等
(相似)三角形的判定与性质、勾股定理等知识求解.
方法应用
4.如图8,为正方形内一点, ,将绕点 按顺时针方向旋转 ,得到(点,的对应点分别为点, ).延长交于点,连接 .
图8
(1)试判断四边形 的形状,并说明理由.
解:四边形 是正方形.
理由:由旋转的性质,得 , .
,,在同一直线上,∴ .
图8
四边形 是矩形.
由旋转的性质,得
四边形 是正方形.
(2)如图9,已知,请猜想线段与 的数量关系并加以证明.
图9
解:.
理由:过点作 于点,则 , .
∵ ,
四边形 是正方形, , .
∴ .
.
图9
在和中,, ,,∴
.
由旋转的性质,得 .
由(1)得,四边形是正方形.
∴ .
图10
5.(2024·山西·中考节选)综合与探究
【图形呈现】如图10,四边形 为菱形,过点作于
点,过点 作于点 .
【猜想证明】
(1)判断四边形 的形状,并说明理由.
解:四边形为矩形.
理由: ,, , .
四边形为菱形, , .
∴ 四边形 为矩形.
【深入探究】
图11
(2)将图11中的绕点 逆时针旋转,
得到,点,的对应点分别为, .如图
11,当线段经过点时, 所在直线分别与
线段,交于点,.猜想线段与 的
数量关系,并说明理由.
图11
解:.
理由: 四边形 为菱形, , .
由旋转的性质,得,
, .
在和中, ,,,∴
,即 .
类型三 与动点有关的四边形综合题
方法解读 解决这类问题的基本策略是“化动为静”,要抓住图形中的等
量关系和各个元素的变化情况,要特别注意一些不变的量、不变的关系
或特殊关系,将其化动为静,由特殊情形(特殊点、特殊值、特殊位置、
特殊图形等)逐步过渡到一般情形,即选取动点运动路径中的任意一个
位置形成静态图形,再由静态图形的性质得出题设中变量间的关系.
方法应用
图12
6.(2024·山东威海·中考节选)如图12,在菱形
中,, , 为对角
线上的动点,以为边作 ,
交射线于点,连接,.点从点 出发,
沿方向以每秒的速度运动至点 处停止.设
的面积为,点的运动时间为 .
图12
(1)求证: .
证明:设与相交于点
四边形 为菱形, ,, .
在和中,, , ,
, .
,∴ .
又 ,
.
(2)求与的函数解析式,并写出自变量 的取值范围.
图12
解:过点作于点,则 .
,
四边形 为菱形, , , ,即 .
,∴ ,
∴ .
∴
∵ , .
微专题练习(九) 与四边形有关的综合题
类型一 与折叠有关的四边形综合题
图1
1.(2025·四川攀枝花·模拟)如图1,将矩形沿 折叠,
使点落在边上的点处,过点作交于点 ,
连接.给出以下结论:;②四边形 是菱
形;;④当,时, 的长
为 .其中正确的是________.(填序号)
图46
提示:由,得 .由折叠的性质,
得,, .从而得
.所以 .故①正确.由此可得,
,所以四边形 是菱形.故
②正确.如图46,连接,交于点 .由菱形的性质,
得,.由 ,
,得.所以,即 .由
此可得,.故③错误.如图46,过点
作于点,则四边形 是矩形,
.由,得 ,
即.解得或
(舍去).因为, ,所以
. 由, ,
得.从而得.所以, 即
.所以 .由此可得,
.故④正确.
图46
2.(2024·山东潍坊·中考)如图2,在矩形中,,点 ,
分别在边,上.将沿折叠,点的对应点 恰好落在对角
线上;将沿折叠,点的对应点恰好也落在对角线 上.
连接, .
图2
图2
(1)求证: .
证明: 四边形是矩形, , , //
.
由折叠的性质,得, ,, .
, .
.
在和 中,, ,,
.
(2)求证:四边形 为平行四边形.
图2
解:由(1)知 ,, ,
四边形 为平行四边形.
类型二 与旋转有关的四边形综合题
图3
3.(2024·吉林·中考)如图3,在平面直角坐标系
中,点的坐标为,点的坐标为 .以
,为边作矩形.若将矩形绕点
顺时针旋转 ,得到矩形,则点 的坐
标为( ).
C
A. B. C. D.
4.(2024·海南·中考)如图4,菱形的边长为2, ,
边在数轴上,将绕点顺时针旋转,点落在数轴上的点 处.若点
表示的数是3,则点 表示的数是( ).
图4
A.1 B. C.0 D.
图4
【答案】D
提示:过点C作的垂线,垂足为点 .由菱形的性质,得,平分 ,.所以 . 从而得 .所以.因为 ,所以 .由此可得,.所以. 所以 .又点表示的数是3,故点A表示的数是 .
5.(2025·湖南衡阳·中考改编)
【问题探究】
(1)如图5(见下页),在正方形中,对角线,相交于点 .
在线段上任取一点(端点除外),连接, .
图5
①将线段绕点逆时针旋转,使点落在的延长线上的点处.当点 在线段上的位置发生变化时, 的大小是否发生变化?请说明理由.
图5
解:的大小不发生变化, .
理由:如图47,过点作, ,垂足分别为点,
四边形是正方形, , .
, .
在和 中,,,
, ,
即 .
②探究与 的数量关系,并说明理由.
图5
图47
解:.
理由:如图47,过点 作交于点,垂足为点,过点 作于点,垂足为点
四边形 是正方形, , , 垂直平分
,四边形 是矩形,
,
,
图47
, ,
, ,
.
【迁移探究】
(2)如图6,将正方形换成菱形,且 ,其他条件不变.试探究与 的数量关系,并说明理由.
图6
解:.
理由: 四边形 是菱形, , , ,
是等边三角形, 垂直平分
,
,∴ .
图48
如图48,过点作交于点 ,过点作交于点,则四边形 是平行四边形, , , ,,都是等边三角形.
.
过点作 于点,则,,
.
类型三 与动点有关的四边形综合题
图7
6.(2024·广东·中考)如图7,菱形 的面积为
24,是的中点,是上的动点.若 的面积
为4,则图中阴影部分的面积为____.
小锦囊 观察图形可发现,
.连接 ,
由是的中点,易得.连接,通过分析 的
面积和的面积的数量关系来得到与 的数量关系,从而计算
出 的面积.
图7
提示:连接,.因为是 的中点,所以
.同理可得
.因为 ,所以
.所以 .所以
.故
.
答案:10
7.(2025·甘肃庆阳·模拟)探究与证明
【图形呈现】
图8
(1)如图8,四边形是正方形,是对角线 上
一点.求证: .
证明:(方法一) 四边形 是正方形, , .
在和中,, ,,
.
(方法二)连接 交于点, 四边形是正方形, ,,即 垂直平分 .
【深入探究】
图9
(2)如图9,在正方形中,是对角线 上一
点,,,垂足分别为点, ,连接
,猜想与 的数量关系,并证明你的猜想.
猜想: .
证明:由(1)可知,
,, .
四边形是矩形.
.
【拓展应用】
(3)如图10,在正方形中,,是对角线 上一点,过点
作于点,于点.则 的最小值为_____.
图10
提示:如图49,连接, 四边形是正方形,
,,.由勾股定理,得 .同
(2)可得,四边形是矩形,则.当时, 最小,
最小值为.故的最小值为 .
图49
同课章节目录
