第2单元多边形的面积应用题专项突破(含解析)-数学五年级上册苏教版
文档属性
| 名称 | 第2单元多边形的面积应用题专项突破(含解析)-数学五年级上册苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 339.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 19:32:47 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第2单元多边形的面积应用题专项突破-数学五年级上册苏教版
一、解答题
1.一块平行四边形地,底长150米,高40米,这块地的面积有多少公顷?在这块地里共收小麦3840千克,平均每公顷收小麦多少千克?
2.下图中,四边形ABCD是一个梯形,已知点A用数对表示为(7,3),点B用数对表示为(2,3)。
(1)图中点C用数对表示为( )。
(2)如果计算这个梯形的面积的列式为(3+5)×3÷2,根据这个算式在方格图中把这个梯形画完整。(每个小正方形的边长为1厘米)
(3)在方格图中画一个与这个梯形面积相等的三角形。
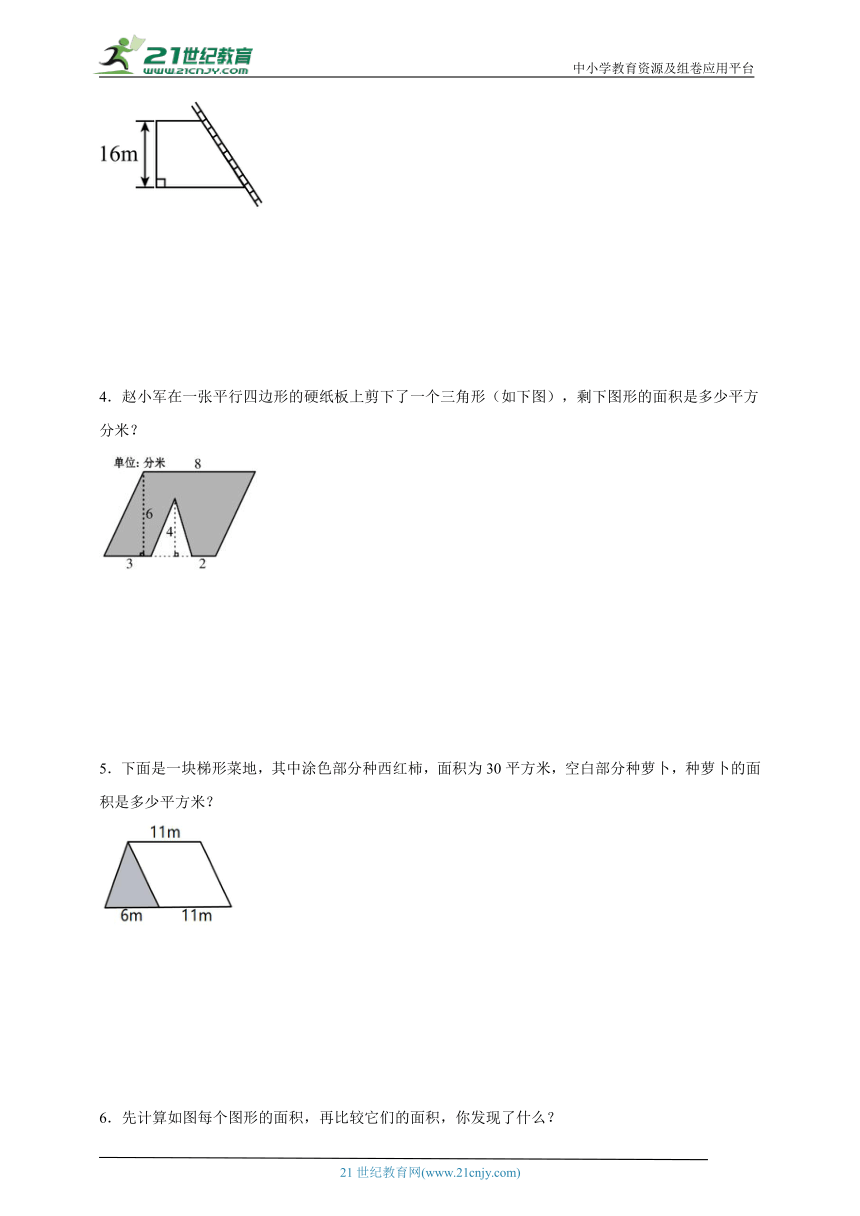
3.2023年9月23日晚,第十九届亚洲运动会开幕式在浙江省杭州市隆重举行,国家主席习近平出席开幕式并宣布本届亚运会开幕。杭州市为美化环境,钱塘江公园靠江堤边围成一个梯形地,种上了杭州市市花桂花,形成了一座桂花园,如图,已知围桂花园的篱笆长48米,这个花园的面积是多少平方米?
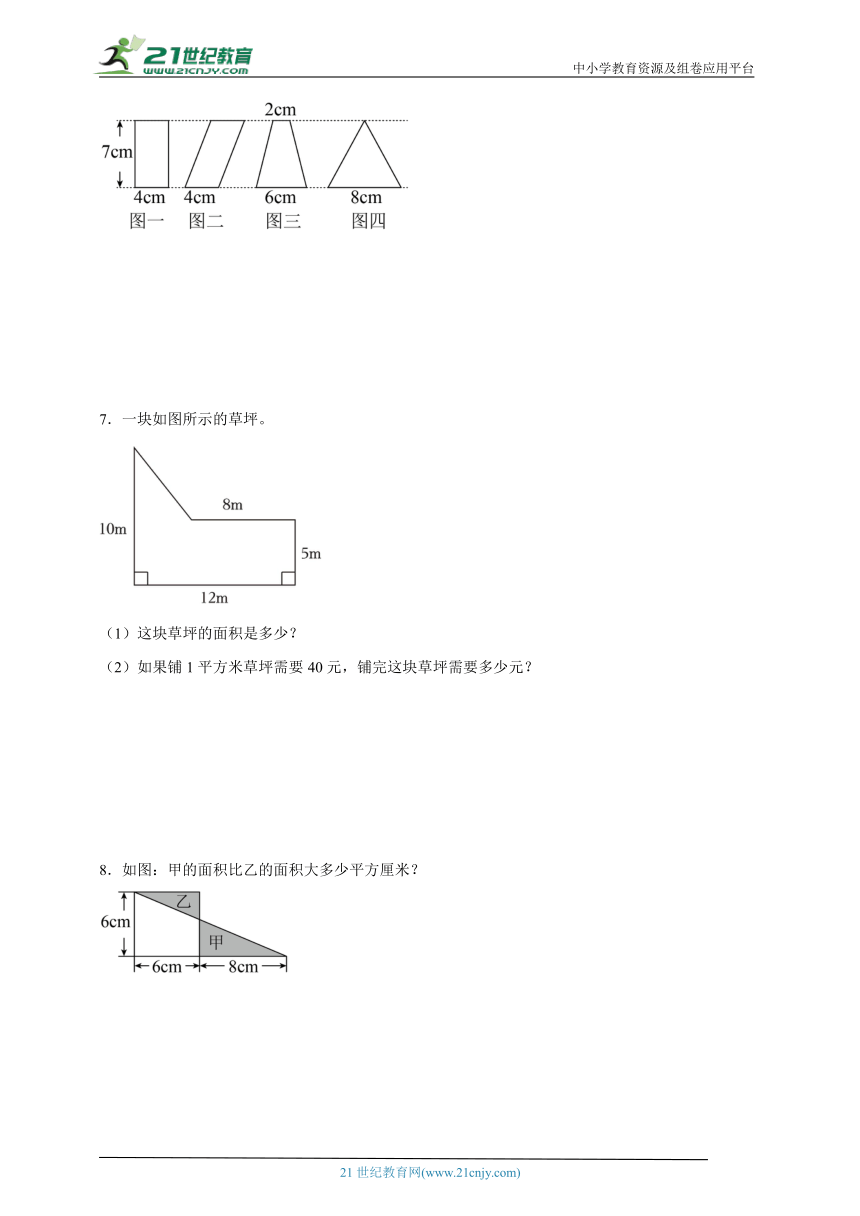
4.赵小军在一张平行四边形的硬纸板上剪下了一个三角形(如下图),剩下图形的面积是多少平方分米?
5.下面是一块梯形菜地,其中涂色部分种西红柿,面积为30平方米,空白部分种萝卜,种萝卜的面积是多少平方米?
6.先计算如图每个图形的面积,再比较它们的面积,你发现了什么?
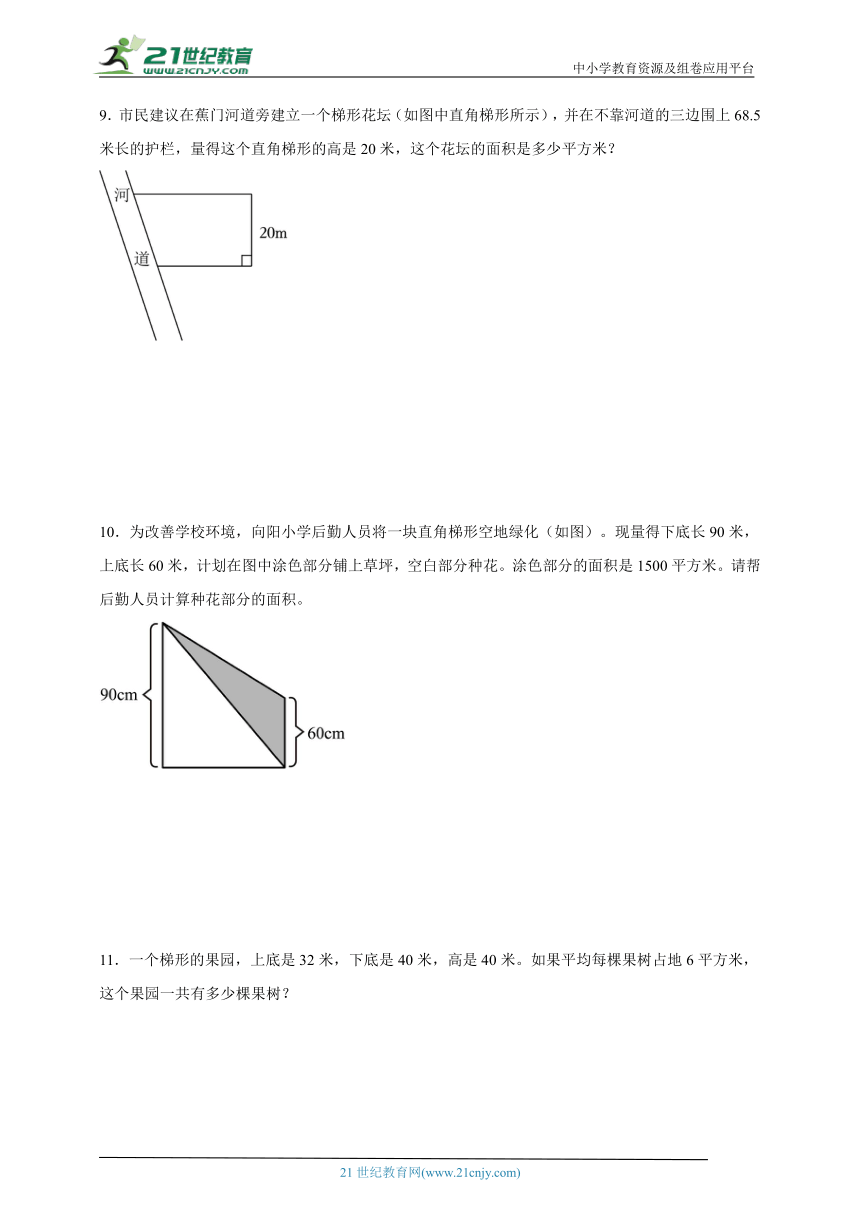
7.一块如图所示的草坪。
(1)这块草坪的面积是多少?
(2)如果铺1平方米草坪需要40元,铺完这块草坪需要多少元?
8.如图:甲的面积比乙的面积大多少平方厘米?
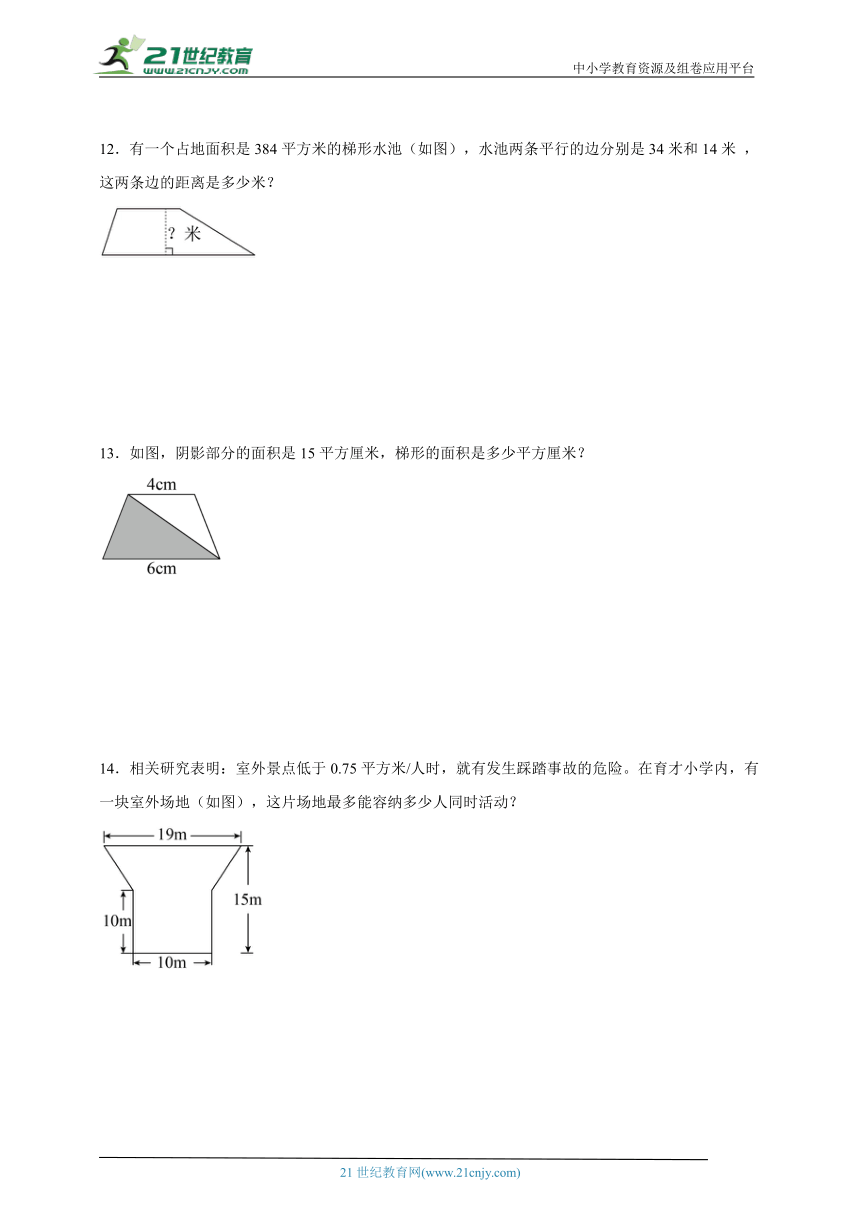
9.市民建议在蕉门河道旁建立一个梯形花坛(如图中直角梯形所示),并在不靠河道的三边围上68.5米长的护栏,量得这个直角梯形的高是20米,这个花坛的面积是多少平方米?
10.为改善学校环境,向阳小学后勤人员将一块直角梯形空地绿化(如图)。现量得下底长90米,上底长60米,计划在图中涂色部分铺上草坪,空白部分种花。涂色部分的面积是1500平方米。请帮后勤人员计算种花部分的面积。
11.一个梯形的果园,上底是32米,下底是40米,高是40米。如果平均每棵果树占地6平方米,这个果园一共有多少棵果树?
12.有一个占地面积是384平方米的梯形水池(如图),水池两条平行的边分别是34米和14米 ,这两条边的距离是多少米?
13.如图,阴影部分的面积是15平方厘米,梯形的面积是多少平方厘米?
14.相关研究表明:室外景点低于0.75平方米/人时,就有发生踩踏事故的危险。在育才小学内,有一块室外场地(如图),这片场地最多能容纳多少人同时活动?
15.疫情防控期间,各学校都采取扫健康码、测量体温、错峰入校等措施保障学生安全。学生入校后需按照指定路线直接到达教室。下图是某学校路上的一个导向箭头,这个导向箭头的面积是多少平方厘米?
16.一块长方形的玉米地,长是32米,宽是15米,玉米地中间有一条3米宽的小路(如图)。如果每平方米土地能收获27千克玉米,这块地一共能收获多少千克玉米?
17.下面这块地种了三种蔬菜。黄瓜种了多少平方米?这块地共有多少平方米?
18.大河蔬菜基地为扩大种植面积,把一块近似梯形的菜地扩建成一个近似平行四边形的菜地,受场地限制,扩建时只把近似梯形的上底延长,下底和高不变(如下图)。
(1)扩建后,新增菜地面积约是( )平方米。
(2)若平均每平方米收菜10千克,这块近似平行四边形的菜地共收菜多少千克?
参考答案:
1.0.6公顷;6400千克
【分析】根据平行四边形面积公式:面积=底×高,代入数据,求出这块地的面积;1公顷=10000平方米;再把面积单位化成公顷;再用这块地收小麦的重量÷这块地的面积,即可解答。
【详解】150×40÷10000
=6000÷10000
=0.6(公顷)
3840÷0.6=6400(千克)
答:这块地的面积有0.6公顷,平均每公顷收小麦6400千克。
2.(1)(5,6)
(2)(3)图见详解
【分析】(1)数对的表示方法:(列数,行数),数对的第一个数表示列,第二个数表示行,分别找出各场所在方格中对应的列数和行数,再用数对表示出来;
(2)梯形面积=(上底+下底)×高÷2,根据面积计算算式可知,上底是3厘米,下底是5厘米,高是3厘米,据此将这个梯形补充完整;
(3)三角形面积=底×高÷2,所以可以取三角形的底为6厘米、高为4厘米,6×4÷2=12(平方厘米),此时三角形的面积和图中梯形的面积相等。
【详解】(1)图中点C用数对表示为(5,6)。
(2)(3)作图如下:
3.256平方米
【分析】因为靠江堤边围成一个梯形,这个梯形是一个直角梯形,篱笆所围的长度=上底+下底+高,则上底+下底=篱笆长-高。直角梯形的面积=(上底+下底)×高÷2=(篱笆长-高)×高÷2。
【详解】
=
=
=(平方米)
答:这个花园的面积是256平方米。
4.42平方分米
【分析】观察图形可知:用平行四边形的面积减去剪下的三角形的面积,即可求出剩下图形的面积。平行四边形的面积=底×高,三角形的面积=底×高÷2,据此解答。
【详解】8×6-(8-3-2)×4÷2
=48-3×4÷2
=48-6
=42(平方分米)
答:剩下图形的面积是42平方分米。
5.110平方米
【分析】从图中可知,西红柿地是一个三角形,萝卜地是一个平行四边形,它们的高相等;
已知三角形的面积和底,根据三角形的高=面积×2÷底,由此求出三角形的高,也是平行四边形的高;
再根据平行四边形的面积=底×高,即可求出种萝卜的面积。
【详解】30×2÷6
=60÷6
=10(米)
11×10=110(平方米)
答:种萝卜的面积是110平方米。
6.图一的面积是28平方厘米,图二的面积28平方厘米,图三的面积28平方厘米,图四的面积28平方厘米。
发现:等底等高的平行四边形的面积相等;高相等,如果三角形的底、梯形的上底和下底的和是平行四边形底的2倍,那么它们的面积也相等。(合理即可,答案不唯一)
【分析】长方形的面积=长×宽,平行四边形面积=底×高,梯形面积=(上底+下底)×高÷2,三角形面积=底×高÷2,据此分别求出各个图形的面积,比较解答即可。
【详解】图一的面积:7×4=28(平方厘米)
图二的面积:4×7=28(平方厘米)
图三的面积:
(2+6)×7÷2
=8×7÷2
=56÷2
=28(平方厘米)
图四的面积:
8×7÷2
=56÷2
=28(平方厘米)
发现:等底等高的平行四边形的面积相等;高相等,如果三角形的底、梯形的上底和下底的和是平行四边形底的2倍,那么它们的面积也相等。(合理即可,答案不唯一)
7.(1)70平方米;(2)2800元
【分析】(1)根据题意可知,这个草坪的面积相当于一个底为(12-8)米、高为(10-5)米的三角形面积加上一个长为12米、宽为5米的长方形面积,根据三角形的面积=底×高÷2和长方形的面积=长×宽,用(12-8)×(10-5)÷2+12×5即可求出这个草坪的面积;
(2)根据单价×数量=总价,用草坪的面积乘40元,即可求出铺完这块草坪需要的总价。
【详解】(1)(12-8)×(10-5)÷2+12×5
=4×5÷2+12×5
=10+60
=70(平方米)
答:这块草坪的面积是70平方米。
(2)70×40=2800(元)
答:铺完这块草坪需要2800元。
8.6平方厘米
【分析】观察图形可知,甲的面积=底是6厘米,高是(6+8)厘米的三角形面积-左下角空白面积;乙的面积=边长是6厘米正方形面积-左下角空白面积,由此可知,求甲的面积比乙的面积大多少平方厘米,即甲的面积-乙的面积=底是6厘米,高是(6+8)厘米的三角形面积-边长是6厘米的正方形面积,根据三角形面积公式:面积=底×高÷2,正方形面积公式:面积=边长×边长,代入数据,即可解答。
【详解】6×(6+8)÷2-6×6
=6×14÷2-36
=84÷2-36
=42-36
=6(平方厘米)
答:甲的面积比乙的面积大6平方厘米。
9.485平方米
【分析】由题意可知,用68.5减去梯形的高是20米就是梯形的上底与下底的和,再根据梯形的面积=(上底+下底)×高÷2,据此代入数值进行计算即可。
【详解】(68.5-20)×20÷2
=48.5×20÷2
=970÷2
=485(平方米)
答:这个花坛的面积是485平方米。
10.2250平方米
【分析】根据题意可知涂色部分为三角形,面积是1500平方米,底是60米,根据三角形的高=面积×2÷底,求出高。三角形的高也是梯形的高,再根据梯形的面积=(上底+下底)×高÷2,求出梯形的面积。用梯形的面积减涂色三角形的面积,求出种花部分的面积。
【详解】1500×2÷60=50(米)
(90+60)×50÷2
=150×50÷2
=7500÷2
=3750(平方米)
3750-1500=2250(平方米)
答:种花部分的面积是2250平方米。
11.240棵
【分析】根据梯形的面积公式:S=(a+b)h÷2,据此代入数值进行计算即可求出果园的面积,再用果园的面积除以6即可求出这个果园一共有多少棵果树。
【详解】(32+40)×40÷2
=72×40÷2
=2880÷2
=1440(平方米)
1440÷6=240(棵)
答:这个果园一共有240棵果树。
12.16米
【分析】由图知:这两条边的距离就是梯形的高。梯形面积=(上底+下底)×高÷2,那么梯形高=面积×2÷(上底+下底),将数据代入其中求出这两条边的距离。
【详解】384×2÷(34+14)
=384×2÷48
=768÷48
=16(米)
答:这两条边的距离是16米。
【点睛】本题考查了梯形的面积,灵活运用梯形的面积公式是解题的关键。
13.25平方厘米
【分析】根据三角形的高=面积×2÷底,求出三角形的高,即梯形的高,再根据梯形面积=(上底+下底)×高÷2,列式解答即可。
【详解】15×2÷6=5(厘米)
(4+6)×5÷2
=10×5÷2
=25(平方厘米)
答:梯形的面积是25平方厘米。
14.230人
【分析】室外场地的面积=上底是19米,下底是10米,高是(15-10)米梯形的面积+边长是10米正方形的面积,根据梯形面积公式:面积=(上底+下底)×高÷2,正方形面积公式:面积=边长×边长,代入数据,求出这块室外场地的面积,再除以0.75平方米,即可求出这片场地最多能容纳多少人同时活动。
【详解】
(10+19)×(15-10)÷2+10×10
=29×5÷2+100
=145÷2+100
=72.5+100
=172.5(平方米)
172.5÷0.75=230(人)
答:这片场地最多能容纳230人同时活动。
15.4200平方厘米
【分析】根据题意可知,这个导向箭头的面积相当于一个长80厘米、宽35厘米的长方形面积加上底是70厘米、高是40厘米的三角形面积;根据长方形的面积=长×宽、三角形的面积=底×高÷2,代入数据求出两个图形的面积,再相加即可。
【详解】
(平方厘米)
答:这个导向箭头的面积是4200平方厘米。
16.11745千克
【分析】根据题意可知,玉米地的面积等于长是32米,宽是15米的长方形面积-底是3米,高是15米的平行四边形面积;根据长方形面积公式:面积=长×宽;平行四边形面积公式:面积=底×高,代入数据,求出玉米地的面积,再乘27,即可解答。
【详解】(32×15-3×15)×27
=(480-45)×27
=435×27
=11745(千克)
答:这块地一共能收11745千克玉米。
17.800平方米;1648平方米
【分析】种黄瓜这块地的面积是一个底为25米,高为32米的平行四边形,根据平行四边形的面积=底×高,代入数据即可求出黄瓜种了多少平方米;种茄子这块地的面积是一个底为15米,高为32米的三角形,种西红柿这块地的面积是一个上底为15米,下底为23米,高为32米的梯形,分别利用三角形和梯形的面积公式,求出这两块地的面积,再加上种黄瓜这块地的面积,即可求出这块地的总面积。
【详解】25×32=800(平方米)
15×32÷2+(15+23)×32÷2+800
=240+38×32÷2+800
=240+608+800
=1648(平方米)
答:黄瓜种了800平方米,这块地共有1648平方米。
【点睛】此题主要考查平行四边形、组合图形的面积的计算方法,同时还需灵活运用三角形、梯形的面积公式。
18.(1)308
(2)15680千克
【分析】(1)由图可知,扩建后的菜地是近似一块底为56米,高为28米的平行四边形,根据底×高=平行四边形,(上底+下底)×高÷2,用扩建后的面积减去原来菜地的面积即可解答。
(2)用扩建后菜地的面积乘每平方米收菜的质量即可解答。
【详解】(1)56×28=1568(平方米)
(34+56)×28÷2
=90×28÷2
=2520÷2
=1260(平方米)
1568-1260=308(平方米)
扩建后,新增菜地面积约是308平方米。
(2)1568×10=15680(千克)
答:这块近似平行四边形的菜地共收菜15680千克。
【点睛】熟练掌握平行四边形和梯形的面积公式是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第2单元多边形的面积应用题专项突破-数学五年级上册苏教版
一、解答题
1.一块平行四边形地,底长150米,高40米,这块地的面积有多少公顷?在这块地里共收小麦3840千克,平均每公顷收小麦多少千克?
2.下图中,四边形ABCD是一个梯形,已知点A用数对表示为(7,3),点B用数对表示为(2,3)。
(1)图中点C用数对表示为( )。
(2)如果计算这个梯形的面积的列式为(3+5)×3÷2,根据这个算式在方格图中把这个梯形画完整。(每个小正方形的边长为1厘米)
(3)在方格图中画一个与这个梯形面积相等的三角形。
3.2023年9月23日晚,第十九届亚洲运动会开幕式在浙江省杭州市隆重举行,国家主席习近平出席开幕式并宣布本届亚运会开幕。杭州市为美化环境,钱塘江公园靠江堤边围成一个梯形地,种上了杭州市市花桂花,形成了一座桂花园,如图,已知围桂花园的篱笆长48米,这个花园的面积是多少平方米?
4.赵小军在一张平行四边形的硬纸板上剪下了一个三角形(如下图),剩下图形的面积是多少平方分米?
5.下面是一块梯形菜地,其中涂色部分种西红柿,面积为30平方米,空白部分种萝卜,种萝卜的面积是多少平方米?
6.先计算如图每个图形的面积,再比较它们的面积,你发现了什么?
7.一块如图所示的草坪。
(1)这块草坪的面积是多少?
(2)如果铺1平方米草坪需要40元,铺完这块草坪需要多少元?
8.如图:甲的面积比乙的面积大多少平方厘米?
9.市民建议在蕉门河道旁建立一个梯形花坛(如图中直角梯形所示),并在不靠河道的三边围上68.5米长的护栏,量得这个直角梯形的高是20米,这个花坛的面积是多少平方米?
10.为改善学校环境,向阳小学后勤人员将一块直角梯形空地绿化(如图)。现量得下底长90米,上底长60米,计划在图中涂色部分铺上草坪,空白部分种花。涂色部分的面积是1500平方米。请帮后勤人员计算种花部分的面积。
11.一个梯形的果园,上底是32米,下底是40米,高是40米。如果平均每棵果树占地6平方米,这个果园一共有多少棵果树?
12.有一个占地面积是384平方米的梯形水池(如图),水池两条平行的边分别是34米和14米 ,这两条边的距离是多少米?
13.如图,阴影部分的面积是15平方厘米,梯形的面积是多少平方厘米?
14.相关研究表明:室外景点低于0.75平方米/人时,就有发生踩踏事故的危险。在育才小学内,有一块室外场地(如图),这片场地最多能容纳多少人同时活动?
15.疫情防控期间,各学校都采取扫健康码、测量体温、错峰入校等措施保障学生安全。学生入校后需按照指定路线直接到达教室。下图是某学校路上的一个导向箭头,这个导向箭头的面积是多少平方厘米?
16.一块长方形的玉米地,长是32米,宽是15米,玉米地中间有一条3米宽的小路(如图)。如果每平方米土地能收获27千克玉米,这块地一共能收获多少千克玉米?
17.下面这块地种了三种蔬菜。黄瓜种了多少平方米?这块地共有多少平方米?
18.大河蔬菜基地为扩大种植面积,把一块近似梯形的菜地扩建成一个近似平行四边形的菜地,受场地限制,扩建时只把近似梯形的上底延长,下底和高不变(如下图)。
(1)扩建后,新增菜地面积约是( )平方米。
(2)若平均每平方米收菜10千克,这块近似平行四边形的菜地共收菜多少千克?
参考答案:
1.0.6公顷;6400千克
【分析】根据平行四边形面积公式:面积=底×高,代入数据,求出这块地的面积;1公顷=10000平方米;再把面积单位化成公顷;再用这块地收小麦的重量÷这块地的面积,即可解答。
【详解】150×40÷10000
=6000÷10000
=0.6(公顷)
3840÷0.6=6400(千克)
答:这块地的面积有0.6公顷,平均每公顷收小麦6400千克。
2.(1)(5,6)
(2)(3)图见详解
【分析】(1)数对的表示方法:(列数,行数),数对的第一个数表示列,第二个数表示行,分别找出各场所在方格中对应的列数和行数,再用数对表示出来;
(2)梯形面积=(上底+下底)×高÷2,根据面积计算算式可知,上底是3厘米,下底是5厘米,高是3厘米,据此将这个梯形补充完整;
(3)三角形面积=底×高÷2,所以可以取三角形的底为6厘米、高为4厘米,6×4÷2=12(平方厘米),此时三角形的面积和图中梯形的面积相等。
【详解】(1)图中点C用数对表示为(5,6)。
(2)(3)作图如下:
3.256平方米
【分析】因为靠江堤边围成一个梯形,这个梯形是一个直角梯形,篱笆所围的长度=上底+下底+高,则上底+下底=篱笆长-高。直角梯形的面积=(上底+下底)×高÷2=(篱笆长-高)×高÷2。
【详解】
=
=
=(平方米)
答:这个花园的面积是256平方米。
4.42平方分米
【分析】观察图形可知:用平行四边形的面积减去剪下的三角形的面积,即可求出剩下图形的面积。平行四边形的面积=底×高,三角形的面积=底×高÷2,据此解答。
【详解】8×6-(8-3-2)×4÷2
=48-3×4÷2
=48-6
=42(平方分米)
答:剩下图形的面积是42平方分米。
5.110平方米
【分析】从图中可知,西红柿地是一个三角形,萝卜地是一个平行四边形,它们的高相等;
已知三角形的面积和底,根据三角形的高=面积×2÷底,由此求出三角形的高,也是平行四边形的高;
再根据平行四边形的面积=底×高,即可求出种萝卜的面积。
【详解】30×2÷6
=60÷6
=10(米)
11×10=110(平方米)
答:种萝卜的面积是110平方米。
6.图一的面积是28平方厘米,图二的面积28平方厘米,图三的面积28平方厘米,图四的面积28平方厘米。
发现:等底等高的平行四边形的面积相等;高相等,如果三角形的底、梯形的上底和下底的和是平行四边形底的2倍,那么它们的面积也相等。(合理即可,答案不唯一)
【分析】长方形的面积=长×宽,平行四边形面积=底×高,梯形面积=(上底+下底)×高÷2,三角形面积=底×高÷2,据此分别求出各个图形的面积,比较解答即可。
【详解】图一的面积:7×4=28(平方厘米)
图二的面积:4×7=28(平方厘米)
图三的面积:
(2+6)×7÷2
=8×7÷2
=56÷2
=28(平方厘米)
图四的面积:
8×7÷2
=56÷2
=28(平方厘米)
发现:等底等高的平行四边形的面积相等;高相等,如果三角形的底、梯形的上底和下底的和是平行四边形底的2倍,那么它们的面积也相等。(合理即可,答案不唯一)
7.(1)70平方米;(2)2800元
【分析】(1)根据题意可知,这个草坪的面积相当于一个底为(12-8)米、高为(10-5)米的三角形面积加上一个长为12米、宽为5米的长方形面积,根据三角形的面积=底×高÷2和长方形的面积=长×宽,用(12-8)×(10-5)÷2+12×5即可求出这个草坪的面积;
(2)根据单价×数量=总价,用草坪的面积乘40元,即可求出铺完这块草坪需要的总价。
【详解】(1)(12-8)×(10-5)÷2+12×5
=4×5÷2+12×5
=10+60
=70(平方米)
答:这块草坪的面积是70平方米。
(2)70×40=2800(元)
答:铺完这块草坪需要2800元。
8.6平方厘米
【分析】观察图形可知,甲的面积=底是6厘米,高是(6+8)厘米的三角形面积-左下角空白面积;乙的面积=边长是6厘米正方形面积-左下角空白面积,由此可知,求甲的面积比乙的面积大多少平方厘米,即甲的面积-乙的面积=底是6厘米,高是(6+8)厘米的三角形面积-边长是6厘米的正方形面积,根据三角形面积公式:面积=底×高÷2,正方形面积公式:面积=边长×边长,代入数据,即可解答。
【详解】6×(6+8)÷2-6×6
=6×14÷2-36
=84÷2-36
=42-36
=6(平方厘米)
答:甲的面积比乙的面积大6平方厘米。
9.485平方米
【分析】由题意可知,用68.5减去梯形的高是20米就是梯形的上底与下底的和,再根据梯形的面积=(上底+下底)×高÷2,据此代入数值进行计算即可。
【详解】(68.5-20)×20÷2
=48.5×20÷2
=970÷2
=485(平方米)
答:这个花坛的面积是485平方米。
10.2250平方米
【分析】根据题意可知涂色部分为三角形,面积是1500平方米,底是60米,根据三角形的高=面积×2÷底,求出高。三角形的高也是梯形的高,再根据梯形的面积=(上底+下底)×高÷2,求出梯形的面积。用梯形的面积减涂色三角形的面积,求出种花部分的面积。
【详解】1500×2÷60=50(米)
(90+60)×50÷2
=150×50÷2
=7500÷2
=3750(平方米)
3750-1500=2250(平方米)
答:种花部分的面积是2250平方米。
11.240棵
【分析】根据梯形的面积公式:S=(a+b)h÷2,据此代入数值进行计算即可求出果园的面积,再用果园的面积除以6即可求出这个果园一共有多少棵果树。
【详解】(32+40)×40÷2
=72×40÷2
=2880÷2
=1440(平方米)
1440÷6=240(棵)
答:这个果园一共有240棵果树。
12.16米
【分析】由图知:这两条边的距离就是梯形的高。梯形面积=(上底+下底)×高÷2,那么梯形高=面积×2÷(上底+下底),将数据代入其中求出这两条边的距离。
【详解】384×2÷(34+14)
=384×2÷48
=768÷48
=16(米)
答:这两条边的距离是16米。
【点睛】本题考查了梯形的面积,灵活运用梯形的面积公式是解题的关键。
13.25平方厘米
【分析】根据三角形的高=面积×2÷底,求出三角形的高,即梯形的高,再根据梯形面积=(上底+下底)×高÷2,列式解答即可。
【详解】15×2÷6=5(厘米)
(4+6)×5÷2
=10×5÷2
=25(平方厘米)
答:梯形的面积是25平方厘米。
14.230人
【分析】室外场地的面积=上底是19米,下底是10米,高是(15-10)米梯形的面积+边长是10米正方形的面积,根据梯形面积公式:面积=(上底+下底)×高÷2,正方形面积公式:面积=边长×边长,代入数据,求出这块室外场地的面积,再除以0.75平方米,即可求出这片场地最多能容纳多少人同时活动。
【详解】
(10+19)×(15-10)÷2+10×10
=29×5÷2+100
=145÷2+100
=72.5+100
=172.5(平方米)
172.5÷0.75=230(人)
答:这片场地最多能容纳230人同时活动。
15.4200平方厘米
【分析】根据题意可知,这个导向箭头的面积相当于一个长80厘米、宽35厘米的长方形面积加上底是70厘米、高是40厘米的三角形面积;根据长方形的面积=长×宽、三角形的面积=底×高÷2,代入数据求出两个图形的面积,再相加即可。
【详解】
(平方厘米)
答:这个导向箭头的面积是4200平方厘米。
16.11745千克
【分析】根据题意可知,玉米地的面积等于长是32米,宽是15米的长方形面积-底是3米,高是15米的平行四边形面积;根据长方形面积公式:面积=长×宽;平行四边形面积公式:面积=底×高,代入数据,求出玉米地的面积,再乘27,即可解答。
【详解】(32×15-3×15)×27
=(480-45)×27
=435×27
=11745(千克)
答:这块地一共能收11745千克玉米。
17.800平方米;1648平方米
【分析】种黄瓜这块地的面积是一个底为25米,高为32米的平行四边形,根据平行四边形的面积=底×高,代入数据即可求出黄瓜种了多少平方米;种茄子这块地的面积是一个底为15米,高为32米的三角形,种西红柿这块地的面积是一个上底为15米,下底为23米,高为32米的梯形,分别利用三角形和梯形的面积公式,求出这两块地的面积,再加上种黄瓜这块地的面积,即可求出这块地的总面积。
【详解】25×32=800(平方米)
15×32÷2+(15+23)×32÷2+800
=240+38×32÷2+800
=240+608+800
=1648(平方米)
答:黄瓜种了800平方米,这块地共有1648平方米。
【点睛】此题主要考查平行四边形、组合图形的面积的计算方法,同时还需灵活运用三角形、梯形的面积公式。
18.(1)308
(2)15680千克
【分析】(1)由图可知,扩建后的菜地是近似一块底为56米,高为28米的平行四边形,根据底×高=平行四边形,(上底+下底)×高÷2,用扩建后的面积减去原来菜地的面积即可解答。
(2)用扩建后菜地的面积乘每平方米收菜的质量即可解答。
【详解】(1)56×28=1568(平方米)
(34+56)×28÷2
=90×28÷2
=2520÷2
=1260(平方米)
1568-1260=308(平方米)
扩建后,新增菜地面积约是308平方米。
(2)1568×10=15680(千克)
答:这块近似平行四边形的菜地共收菜15680千克。
【点睛】熟练掌握平行四边形和梯形的面积公式是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
