4.2角(预习衔接.夯实基础.含解析)-2025-2026学年七年级上册数学北师大版(2024)
文档属性
| 名称 | 4.2角(预习衔接.夯实基础.含解析)-2025-2026学年七年级上册数学北师大版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 226.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 20:42:05 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
预习衔接.夯实基础 角
一.选择题(共5小题)
1.(2024秋 绥棱县期末)图书馆在剧院的东偏南30°方向500米处,那么剧院在图书馆的( )
A.东偏南30°方向500米处
B.南偏东60°方向500米处
C.北偏西30°方向500米处
D.西偏北30°方向500米处
2.(2024春 普洱期末)如图,把一张长方形纸片沿对角线BD折叠,∠CBD=25°,则∠ABF的度数是( )
A.25° B.30° C.40° D.50°
3.(2024秋 凤阳县期末)如图,方格纸中的∠1和∠2的大小关系是( )
A.∠1=∠2 B.∠2=2∠1
C.∠2=90°+∠1 D.∠1+∠2=180°
4.(2024秋 文山市期末)如图,在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为( )
A.69° B.111° C.129° D.141°
5.(2024秋 东莞市期末)如图,已知∠AOB=α,∠BOC=β,OM平分∠AOC,ON平分∠BOC,则∠MON的度数是( )
A.β B.(α﹣β) C.αβ D.α
二.填空题(共5小题)
6.(2024秋 栾城区期中)如图,点O和点C分别是长方形边上的一点,分别沿着OC、OD对折,使得点A和点B分别落在点A'和点B',并且点O、A'和B'在同一条直线上,∠COD= .
7.(2024秋 广州期中)如图,经测量,B处在A处的南偏西55°的方向,C处在A处的南偏东10°方向,C处在B处的北偏东78°方向,求∠C的度数 .
8.(2024秋 泊头市期末)如图,将一副三角板叠放在一起,使直角顶点重合于点O.
(1)比较大小:∠AOD ∠BOC;(填“>”“<”或“=”)
(2)若∠COD=29°40',则∠AOB的度数是 .
9.(2024秋 汉台区期末)如图,O为直线AB上一点,将一直角三角板(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的上方.将三角板绕点O以每秒3°的速度沿逆时针方向旋转一周.则经过 秒后,MN⊥AB.
10.(2024秋 镇平县期末)如图所示的网格是正方形网格,∠DEF ∠ABC.(填“>”,“=”或“<”)
三.解答题(共5小题)
11.(2024秋 临洮县期中)如图,B岛在A岛的南偏西40°方向,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东80°方向,求从C岛看A,B两岛的视角∠ACB的度数.
12.(2024秋 杜尔伯特县期末)如图,已知∠AOB=120°,OC是∠AOB内的一条射线,且∠AOC:∠BOC=1:2.
(1)求∠AOC的度数;
(2)过点O作射线OD,若∠AOD∠AOB,求∠COD的度数.
13.(2024秋 凉山州期末)如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
14.(2024春 阳谷县期末)如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
(1)射线OC的方向是 ;
(2)求∠COD的度数;
(3)若射线OE平分∠COD,求∠AOE的度数.
15.(2024秋 丰润区期末)【实践活动】
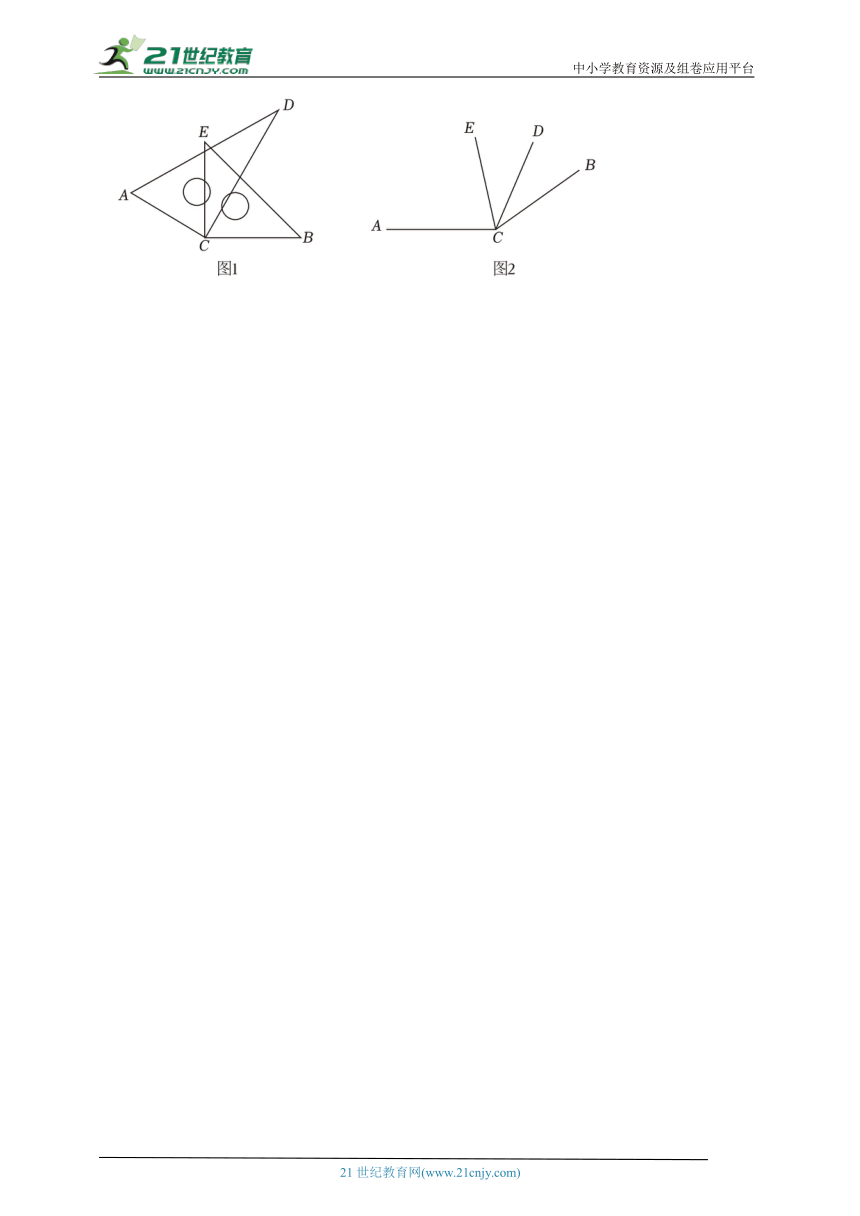
如图1,将一副三角板的直角顶点重合摆放.
(1)∠ACE与∠BCD的大小关系是∠ACE ∠BCD.(填“>”“=”或“<”)
(2)∠ACB与∠DCE之间的数量关系是 .
【拓展探究】
(3)如图2,若∠ACD≠∠BCE,且∠ACD+∠BCE=180°,探索∠ACB与∠DCE之间的数量关系,并说明理由.
预习衔接.夯实基础 角
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 绥棱县期末)图书馆在剧院的东偏南30°方向500米处,那么剧院在图书馆的( )
A.东偏南30°方向500米处
B.南偏东60°方向500米处
C.北偏西30°方向500米处
D.西偏北30°方向500米处
【考点】方向角.
【专题】线段、角、相交线与平行线;运算能力.
【答案】D
【分析】根据方向角的定义,即可解答.
【解答】解:图书馆在剧院的东偏南30°方向500米处,那么剧院在图书馆的西偏北30° 方向500米处,
故选:D.
【点评】本题考查了方向角,熟练掌握方向角的定义是解题的关键.
2.(2024春 普洱期末)如图,把一张长方形纸片沿对角线BD折叠,∠CBD=25°,则∠ABF的度数是( )
A.25° B.30° C.40° D.50°
【考点】角的计算.
【专题】计算题;运算能力.
【答案】C
【分析】利用折叠的特性可得∠CBD=∠EBD=25°,再利用正方形的性质∠ABC=90°,则∠ABE=90°﹣∠EBC,结论可得.
【解答】解:由折叠可得:∠CBD=∠EBD=25°,
则∠EBC=∠CBD+∠EBD=50°.
∵四边形ABCD是长方形,
∴∠ABC=90°,
∴∠ABF=90°﹣∠EBC=40°.
故选:C.
【点评】本题主要考查了角的计算,折叠的性质,正方形的性质,利用折叠是全等变换得出:∠CBD=∠EBD,这是解题的关键.
3.(2024秋 凤阳县期末)如图,方格纸中的∠1和∠2的大小关系是( )
A.∠1=∠2 B.∠2=2∠1
C.∠2=90°+∠1 D.∠1+∠2=180°
【考点】角的大小比较.
【专题】线段、角、相交线与平行线;推理能力.
【答案】D
【分析】先观察图形可知:∠BAC=∠DEF=90°,AB=DE,AC=EF,利用全等三角形的判定定理证明△ABC≌△EDF,从而证明∠3=∠4,再根据∠2=90°+∠4,∠1+∠3=90°,进行代换即可求出答案.
【解答】解:如图所示:
由题意可知:∠BAC=∠DEF=90°,AB=DE,AC=EF,
∴△ABC≌△EDF,
∴∠3=∠4,
∵∠1+∠3=90°,
∴∠3=90°﹣∠1,
∵∠2=90°+∠4,
∴∠2=90°+∠3=90°+90°﹣∠1=180°﹣∠1,
∴∠1+∠2=180°,
故选:D.
【点评】本题主要考查了角的大小比较,解题关键熟练掌握全等三角形的性质和判定.
4.(2024秋 文山市期末)如图,在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为( )
A.69° B.111° C.129° D.141°
【考点】方向角.
【专题】线段、角、相交线与平行线;运算能力.
【答案】D
【分析】利用方向角的定义求解即可.
【解答】解:∠AOB=90°﹣54°+90°+15°=141°.
故选:D.
【点评】本题主要考查了方向角,解题的关键是正确理解方向角的定义.
5.(2024秋 东莞市期末)如图,已知∠AOB=α,∠BOC=β,OM平分∠AOC,ON平分∠BOC,则∠MON的度数是( )
A.β B.(α﹣β) C.αβ D.α
【考点】角的计算.
【答案】D
【分析】求出∠AOC,根据角平分线定义求出∠NOC和∠MOC,相减即可求出答案.
【解答】解:∵∠AOB=α,∠BOC=β,
∴∠AOC=α+β,
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠NOC∠BOC,∠MOC∠AOC,
∴∠MON=∠MOC﹣∠NOC.
故选:D.
【点评】本题考查了角平分线定义,角的有关计算的应用,解此题的关键是求出∠NOC和∠MOC的大小.
二.填空题(共5小题)
6.(2024秋 栾城区期中)如图,点O和点C分别是长方形边上的一点,分别沿着OC、OD对折,使得点A和点B分别落在点A'和点B',并且点O、A'和B'在同一条直线上,∠COD= 90° .
【考点】角的计算.
【专题】线段、角、相交线与平行线;运算能力.
【答案】90°.
【分析】根据折叠的性质可得∠A′OC=∠AOC,∠B′OD=∠BOD,再由∠COD=∠A′OC+∠B′OD进行计算即可得出答案.
【解答】解:根据题意可得,
∠A′OC=∠AOC,∠B′OD=∠BOD,
∵∠COD=∠A′OC+∠B′OD,
∴(∠A0A′+∠BOB′)90°.
故答案为:90°.
【点评】本题主要考查了角的计算,根据折叠的性质运用角的计算方法进行求解是解决本题的关键.
7.(2024秋 广州期中)如图,经测量,B处在A处的南偏西55°的方向,C处在A处的南偏东10°方向,C处在B处的北偏东78°方向,求∠C的度数 92° .
【考点】方向角.
【专题】线段、角、相交线与平行线;推理能力.
【答案】92°.
【分析】根据题意得∠BAD=55°,∠CAD=10°,∠EBC=78°.则∠BAC=∠BAD+∠DAC=65°.进一步得∠EBA=∠BAD=55°,则∠ABC=23°,利用三角形内角和即可求得∠ACB.
【解答】解:如图,
根据方向角的定义,可得∠BAD=55°,∠CAD=10°,∠EBC=78°.
则∠BAC=∠BAD+∠DAC=55°+10°=65°.
∵AD,EB是正南正北方向,
∴BE∥AD,
∴∠EBA=∠BAD=55°,
∵∠EBC=78°,
∴∠ABC=78°﹣55°=23°,
∴根据三角形内角和定理得,∠ACB=180°﹣∠ABC﹣∠BAC=180°﹣65°﹣23°=92°.
所以∠C的度数为92°.
故答案为:92°.
【点评】本题主要考查方向角,关键是相关定义的熟练掌握.
8.(2024秋 泊头市期末)如图,将一副三角板叠放在一起,使直角顶点重合于点O.
(1)比较大小:∠AOD = ∠BOC;(填“>”“<”或“=”)
(2)若∠COD=29°40',则∠AOB的度数是 151°20′ .
【考点】角的大小比较;度分秒的换算.
【专题】线段、角、相交线与平行线;运算能力.
【答案】(1)=;(2)151°20′.
【分析】(1)根据直角三角板的性质即可得出结论;
(2)根据直角三角板的性质求出∠AOD、∠BOC的度数,进而可得出结论.
【解答】解:(1)∵∠AOD+∠DOC=90°,∠BOC+∠DOC=90°,
∴∠AOD=∠BOC.
故答案为:=;
(2)∵∠AOD+∠DOC=90°,∠BOC+∠DOC=90°,∠DOC=29°40',
∴∠AOD=∠BOC=90°﹣29°40′=61°20′,
∴∠AOB=∠AOD+∠BOC+∠DOC=61°20′+61°20′+29°40'=151°20′.
故答案为:151°20′.
【点评】本题考查的是角的大小比较,熟知直角三角板的性质是解题的关键.
9.(2024秋 汉台区期末)如图,O为直线AB上一点,将一直角三角板(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的上方.将三角板绕点O以每秒3°的速度沿逆时针方向旋转一周.则经过 10或70 秒后,MN⊥AB.
【考点】角的计算.
【专题】计算题;线段、角、相交线与平行线;几何直观;运算能力.
【答案】10或70.
【分析】认真读懂题意,分析整个转动过程会发现,转动一周有两个时刻出现MN⊥AB,通过位置确定角的度数,再分别讨论计算出时间即可.
【解答】解:根据旋转的性质,可知MN从原先的位置转到MN⊥AB,要经过30°或180°+30°=210°,
∴30÷3=10(秒);210÷3=70(秒),
故答案为:10或70.
【点评】本题考查了角的计算,解题的关键是读懂题意,掌握旋转中角的变化.
10.(2024秋 镇平县期末)如图所示的网格是正方形网格,∠DEF < ∠ABC.(填“>”,“=”或“<”)
【考点】角的大小比较.
【专题】几何直观.
【答案】<.
【分析】过点E向下作竖直线EG,根据网格线可得∠ABC=∠DEG,∠EDG>∠DEF,即可比较∠DEF和∠ABC的大小.
【解答】解:过点E向下作竖直线EG,
由网格线可得,∠ABC=∠DEG=45°,
∵∠EDG>∠DEF,
∴∠DEF<∠ABC,
故答案为:<.
【点评】本题主要考查角的大小比较,利用网格线得出∠ABC=∠DEG=45°是解题的关键.
三.解答题(共5小题)
11.(2024秋 临洮县期中)如图,B岛在A岛的南偏西40°方向,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东80°方向,求从C岛看A,B两岛的视角∠ACB的度数.
【考点】方向角.
【专题】线段、角、相交线与平行线;几何直观.
【答案】85°.
【分析】由题意得:BE∥AD,∠BAD=40°,∠CAD=15°,∠EBC=80°,再根据平行线的性质以及三角形内角和定理,即可得到∠ACB的度数.
【解答】解:如图,由题意得:BE∥AD,∠BAD=40°,∠CAD=15°,∠EBC=80°,
∴∠EBA=∠BAD=40°,
∴∠BAC=∠BAD+∠CAD=40°+15°=55°,
∴∠CBA=∠EBC﹣∠EBA=80°﹣40°=40°,
∴∠ACB=180°﹣∠BAC﹣∠ABC
=180°﹣55°﹣40°=85°,
答:从C岛看A,B两岛的视角∠ACB的度数为85°.
【点评】本题主要考查了方向角,方向角是表示方向的角;以正北,正南方向为基准,来描述物体所处的方向.
12.(2024秋 杜尔伯特县期末)如图,已知∠AOB=120°,OC是∠AOB内的一条射线,且∠AOC:∠BOC=1:2.
(1)求∠AOC的度数;
(2)过点O作射线OD,若∠AOD∠AOB,求∠COD的度数.
【考点】角的计算.
【专题】线段、角、相交线与平行线;运算能力.
【答案】见试题解答内容
【分析】(1)根据∠AOC:∠BOC=1:2,即可求解;
(2)先求出∠COM,再求出∠CON,相加即可求解.
【解答】解:(1)∵∠AOC:∠BOC=1:2,∠AOB=120°,
∴∠AOC∠AOB120°=40°;
(2)∵∠AOD∠AOB,
∴∠AOD=60°,
当OD在∠AOB内时,
∠COD=∠AOD﹣∠AOC=20°,
当OD在∠AOB外时,
∠COD=∠AOC+∠AOD=100°.
故∠COD的度数为20°或100°.
【点评】本题考查了角的计算及角平分线,掌握角的特点及比例的意义是解决问题的关键.
13.(2024秋 凉山州期末)如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
【考点】角的计算.
【专题】计算题.
【答案】见试题解答内容
【分析】(1)根据角平分线定义得到∠AOC∠EOC70°=35°,然后根据对顶角相等得到∠BOD=∠AOC=35°;
(2)先设∠EOC=2x,∠EOD=3x,根据平角的定义得2x+3x=180°,解得x=36°,则∠EOC=2x=72°,然后与(1)的计算方法一样.
【解答】解:(1)∵OA平分∠EOC,
∴∠AOC∠EOC70°=35°,
∴∠BOD=∠AOC=35°;
(2)设∠EOC=2x,∠EOD=3x,根据题意得2x+3x=180°,解得x=36°,
∴∠EOC=2x=72°,
∴∠AOC∠EOC72°=36°,
∴∠BOD=∠AOC=36°.
【点评】考查了角的计算:1直角=90°;1平角=180°.也考查了角平分线的定义和对顶角的性质.
14.(2024春 阳谷县期末)如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
(1)射线OC的方向是 北偏东70° ;
(2)求∠COD的度数;
(3)若射线OE平分∠COD,求∠AOE的度数.
【考点】方向角.
【答案】见试题解答内容
【分析】(1)先求出∠AOB=55°,再求得∠NOC的度数,即可确定OC的方向;
(2)根据∠AOB=55°,∠AOC=∠AOB,得出∠BOC=110°,进而求出∠COD的度数;
(3)根据射线OE平分∠COD,即可求出∠COE=35°再利用∠AOC=55°求出答案即可.
【解答】解:(1)∵OB的方向是北偏西40°,OA的方向是北偏东15°,
∴∠NOB=40°,∠NOA=15°,
∴∠AOB=∠NOB+∠NOA=55°,
∵∠AOB=∠AOC,
∴∠AOC=55°,
∴∠NOC=∠NOA+∠AOC=70°,
∴OC的方向是北偏东70°;
故答案为:北偏东70°;
(2)∵∠AOB=55°,∠AOC=∠AOB,
∴∠BOC=110°.
又∵射线OD是OB的反向延长线,
∴∠BOD=180°.
∴∠COD=180°﹣110°=70°.
(3)∵∠COD=70°,OE平分∠COD,
∴∠COE=35°.
∵∠AOC=55°.
∴∠AOE=90°.
【点评】此题主要考查了方向角的表达即方向角一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)多少度.
15.(2024秋 丰润区期末)【实践活动】
如图1,将一副三角板的直角顶点重合摆放.
(1)∠ACE与∠BCD的大小关系是∠ACE = ∠BCD.(填“>”“=”或“<”)
(2)∠ACB与∠DCE之间的数量关系是 ∠ACB+∠DCE=180° .
【拓展探究】
(3)如图2,若∠ACD≠∠BCE,且∠ACD+∠BCE=180°,探索∠ACB与∠DCE之间的数量关系,并说明理由.
【考点】角的大小比较;角的计算.
【专题】线段、角、相交线与平行线;几何直观;运算能力;推理能力.
【答案】(1)=;
(2)∠ACB+∠DCE=180°,理由见解答过程;
(3)∠ACB+∠DCE=180°,理由见解答过程.
【分析】(1)依题意得∠ACD=90°,∠ECB=90°,进而得∠ACE+∠DCE=90°,∠DCE+∠BCD=90°,然后根据同角的余角相等可得出答案;
(2)由∠ACD=90°,∠ECB=90°得∠ACE+∠DCE=90°,∠DCE+∠BCD=90°,则∠ACE+2∠DCE+∠BCD=180°,然而∠ACB+∠DCE=∠ACE+2∠DCE+∠BCD=180°;据此可得∠ACB与∠DCE之间的数量关系;
(3)先由∠ACD+∠BCE=180°得∠ACE+2∠DCE+∠BCD=180°,进而得∠ACB+∠DCE=∠ACE+2∠DCE+∠BCD=180°,据此可得∠ACB与∠DCE之间的数量关系.
【解答】解:(1)依题意得:∠ACD=90°,∠ECB=90°,
∴∠ACE+∠DCE=90°,∠DCE+∠BCD=90°,
∴∠ACE=∠BCD.
故答案为:=.
(2)∠ACB与∠DCE之间的数量关系:∠ACB+∠DCE=180°,理由如下:
∵∠ACD=90°,∠ECB=90°,
∴∠ACE+∠DCE=90°,∠DCE+∠BCD=90°,
∵∠ACE+∠DCE+∠DCE+∠BCD=90°+90°,
∴∠ACE+2∠DCE+∠BCD=180°,
又∵∠ACB=∠ACE+∠DCE+∠BCD,
∴∠ACB+∠DCE=∠ACE+∠DCE+∠BCD+∠DCE=∠ACE+2∠DCE+∠BCD=180°;
(3)∠ACB与∠DCE之间的数量关系是:∠ACB+∠DCE=180°,理由如下:
∵∠ACD=∠ACE+∠DCE,∠BCE=∠DCE+∠BCD,
又∵∠ACD+∠BCE=180°,
∴∠ACE+∠DCE+∠DCE+∠BCD=180°,
即:∠ACE+2∠DCE+∠BCD=180°,
∴∠ACB+∠DCE=∠ACE+∠DCE+∠BCD+∠DCE=∠ACE+2∠DCE+∠BCD=180°.
【点评】此题主要考查了角的计算,同角的余角相等,准确识图,理解同角的余角相等,熟练掌握角的计算是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.夯实基础 角
一.选择题(共5小题)
1.(2024秋 绥棱县期末)图书馆在剧院的东偏南30°方向500米处,那么剧院在图书馆的( )
A.东偏南30°方向500米处
B.南偏东60°方向500米处
C.北偏西30°方向500米处
D.西偏北30°方向500米处
2.(2024春 普洱期末)如图,把一张长方形纸片沿对角线BD折叠,∠CBD=25°,则∠ABF的度数是( )
A.25° B.30° C.40° D.50°
3.(2024秋 凤阳县期末)如图,方格纸中的∠1和∠2的大小关系是( )
A.∠1=∠2 B.∠2=2∠1
C.∠2=90°+∠1 D.∠1+∠2=180°
4.(2024秋 文山市期末)如图,在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为( )
A.69° B.111° C.129° D.141°
5.(2024秋 东莞市期末)如图,已知∠AOB=α,∠BOC=β,OM平分∠AOC,ON平分∠BOC,则∠MON的度数是( )
A.β B.(α﹣β) C.αβ D.α
二.填空题(共5小题)
6.(2024秋 栾城区期中)如图,点O和点C分别是长方形边上的一点,分别沿着OC、OD对折,使得点A和点B分别落在点A'和点B',并且点O、A'和B'在同一条直线上,∠COD= .
7.(2024秋 广州期中)如图,经测量,B处在A处的南偏西55°的方向,C处在A处的南偏东10°方向,C处在B处的北偏东78°方向,求∠C的度数 .
8.(2024秋 泊头市期末)如图,将一副三角板叠放在一起,使直角顶点重合于点O.
(1)比较大小:∠AOD ∠BOC;(填“>”“<”或“=”)
(2)若∠COD=29°40',则∠AOB的度数是 .
9.(2024秋 汉台区期末)如图,O为直线AB上一点,将一直角三角板(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的上方.将三角板绕点O以每秒3°的速度沿逆时针方向旋转一周.则经过 秒后,MN⊥AB.
10.(2024秋 镇平县期末)如图所示的网格是正方形网格,∠DEF ∠ABC.(填“>”,“=”或“<”)
三.解答题(共5小题)
11.(2024秋 临洮县期中)如图,B岛在A岛的南偏西40°方向,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东80°方向,求从C岛看A,B两岛的视角∠ACB的度数.
12.(2024秋 杜尔伯特县期末)如图,已知∠AOB=120°,OC是∠AOB内的一条射线,且∠AOC:∠BOC=1:2.
(1)求∠AOC的度数;
(2)过点O作射线OD,若∠AOD∠AOB,求∠COD的度数.
13.(2024秋 凉山州期末)如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
14.(2024春 阳谷县期末)如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
(1)射线OC的方向是 ;
(2)求∠COD的度数;
(3)若射线OE平分∠COD,求∠AOE的度数.
15.(2024秋 丰润区期末)【实践活动】
如图1,将一副三角板的直角顶点重合摆放.
(1)∠ACE与∠BCD的大小关系是∠ACE ∠BCD.(填“>”“=”或“<”)
(2)∠ACB与∠DCE之间的数量关系是 .
【拓展探究】
(3)如图2,若∠ACD≠∠BCE,且∠ACD+∠BCE=180°,探索∠ACB与∠DCE之间的数量关系,并说明理由.
预习衔接.夯实基础 角
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 绥棱县期末)图书馆在剧院的东偏南30°方向500米处,那么剧院在图书馆的( )
A.东偏南30°方向500米处
B.南偏东60°方向500米处
C.北偏西30°方向500米处
D.西偏北30°方向500米处
【考点】方向角.
【专题】线段、角、相交线与平行线;运算能力.
【答案】D
【分析】根据方向角的定义,即可解答.
【解答】解:图书馆在剧院的东偏南30°方向500米处,那么剧院在图书馆的西偏北30° 方向500米处,
故选:D.
【点评】本题考查了方向角,熟练掌握方向角的定义是解题的关键.
2.(2024春 普洱期末)如图,把一张长方形纸片沿对角线BD折叠,∠CBD=25°,则∠ABF的度数是( )
A.25° B.30° C.40° D.50°
【考点】角的计算.
【专题】计算题;运算能力.
【答案】C
【分析】利用折叠的特性可得∠CBD=∠EBD=25°,再利用正方形的性质∠ABC=90°,则∠ABE=90°﹣∠EBC,结论可得.
【解答】解:由折叠可得:∠CBD=∠EBD=25°,
则∠EBC=∠CBD+∠EBD=50°.
∵四边形ABCD是长方形,
∴∠ABC=90°,
∴∠ABF=90°﹣∠EBC=40°.
故选:C.
【点评】本题主要考查了角的计算,折叠的性质,正方形的性质,利用折叠是全等变换得出:∠CBD=∠EBD,这是解题的关键.
3.(2024秋 凤阳县期末)如图,方格纸中的∠1和∠2的大小关系是( )
A.∠1=∠2 B.∠2=2∠1
C.∠2=90°+∠1 D.∠1+∠2=180°
【考点】角的大小比较.
【专题】线段、角、相交线与平行线;推理能力.
【答案】D
【分析】先观察图形可知:∠BAC=∠DEF=90°,AB=DE,AC=EF,利用全等三角形的判定定理证明△ABC≌△EDF,从而证明∠3=∠4,再根据∠2=90°+∠4,∠1+∠3=90°,进行代换即可求出答案.
【解答】解:如图所示:
由题意可知:∠BAC=∠DEF=90°,AB=DE,AC=EF,
∴△ABC≌△EDF,
∴∠3=∠4,
∵∠1+∠3=90°,
∴∠3=90°﹣∠1,
∵∠2=90°+∠4,
∴∠2=90°+∠3=90°+90°﹣∠1=180°﹣∠1,
∴∠1+∠2=180°,
故选:D.
【点评】本题主要考查了角的大小比较,解题关键熟练掌握全等三角形的性质和判定.
4.(2024秋 文山市期末)如图,在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为( )
A.69° B.111° C.129° D.141°
【考点】方向角.
【专题】线段、角、相交线与平行线;运算能力.
【答案】D
【分析】利用方向角的定义求解即可.
【解答】解:∠AOB=90°﹣54°+90°+15°=141°.
故选:D.
【点评】本题主要考查了方向角,解题的关键是正确理解方向角的定义.
5.(2024秋 东莞市期末)如图,已知∠AOB=α,∠BOC=β,OM平分∠AOC,ON平分∠BOC,则∠MON的度数是( )
A.β B.(α﹣β) C.αβ D.α
【考点】角的计算.
【答案】D
【分析】求出∠AOC,根据角平分线定义求出∠NOC和∠MOC,相减即可求出答案.
【解答】解:∵∠AOB=α,∠BOC=β,
∴∠AOC=α+β,
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠NOC∠BOC,∠MOC∠AOC,
∴∠MON=∠MOC﹣∠NOC.
故选:D.
【点评】本题考查了角平分线定义,角的有关计算的应用,解此题的关键是求出∠NOC和∠MOC的大小.
二.填空题(共5小题)
6.(2024秋 栾城区期中)如图,点O和点C分别是长方形边上的一点,分别沿着OC、OD对折,使得点A和点B分别落在点A'和点B',并且点O、A'和B'在同一条直线上,∠COD= 90° .
【考点】角的计算.
【专题】线段、角、相交线与平行线;运算能力.
【答案】90°.
【分析】根据折叠的性质可得∠A′OC=∠AOC,∠B′OD=∠BOD,再由∠COD=∠A′OC+∠B′OD进行计算即可得出答案.
【解答】解:根据题意可得,
∠A′OC=∠AOC,∠B′OD=∠BOD,
∵∠COD=∠A′OC+∠B′OD,
∴(∠A0A′+∠BOB′)90°.
故答案为:90°.
【点评】本题主要考查了角的计算,根据折叠的性质运用角的计算方法进行求解是解决本题的关键.
7.(2024秋 广州期中)如图,经测量,B处在A处的南偏西55°的方向,C处在A处的南偏东10°方向,C处在B处的北偏东78°方向,求∠C的度数 92° .
【考点】方向角.
【专题】线段、角、相交线与平行线;推理能力.
【答案】92°.
【分析】根据题意得∠BAD=55°,∠CAD=10°,∠EBC=78°.则∠BAC=∠BAD+∠DAC=65°.进一步得∠EBA=∠BAD=55°,则∠ABC=23°,利用三角形内角和即可求得∠ACB.
【解答】解:如图,
根据方向角的定义,可得∠BAD=55°,∠CAD=10°,∠EBC=78°.
则∠BAC=∠BAD+∠DAC=55°+10°=65°.
∵AD,EB是正南正北方向,
∴BE∥AD,
∴∠EBA=∠BAD=55°,
∵∠EBC=78°,
∴∠ABC=78°﹣55°=23°,
∴根据三角形内角和定理得,∠ACB=180°﹣∠ABC﹣∠BAC=180°﹣65°﹣23°=92°.
所以∠C的度数为92°.
故答案为:92°.
【点评】本题主要考查方向角,关键是相关定义的熟练掌握.
8.(2024秋 泊头市期末)如图,将一副三角板叠放在一起,使直角顶点重合于点O.
(1)比较大小:∠AOD = ∠BOC;(填“>”“<”或“=”)
(2)若∠COD=29°40',则∠AOB的度数是 151°20′ .
【考点】角的大小比较;度分秒的换算.
【专题】线段、角、相交线与平行线;运算能力.
【答案】(1)=;(2)151°20′.
【分析】(1)根据直角三角板的性质即可得出结论;
(2)根据直角三角板的性质求出∠AOD、∠BOC的度数,进而可得出结论.
【解答】解:(1)∵∠AOD+∠DOC=90°,∠BOC+∠DOC=90°,
∴∠AOD=∠BOC.
故答案为:=;
(2)∵∠AOD+∠DOC=90°,∠BOC+∠DOC=90°,∠DOC=29°40',
∴∠AOD=∠BOC=90°﹣29°40′=61°20′,
∴∠AOB=∠AOD+∠BOC+∠DOC=61°20′+61°20′+29°40'=151°20′.
故答案为:151°20′.
【点评】本题考查的是角的大小比较,熟知直角三角板的性质是解题的关键.
9.(2024秋 汉台区期末)如图,O为直线AB上一点,将一直角三角板(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的上方.将三角板绕点O以每秒3°的速度沿逆时针方向旋转一周.则经过 10或70 秒后,MN⊥AB.
【考点】角的计算.
【专题】计算题;线段、角、相交线与平行线;几何直观;运算能力.
【答案】10或70.
【分析】认真读懂题意,分析整个转动过程会发现,转动一周有两个时刻出现MN⊥AB,通过位置确定角的度数,再分别讨论计算出时间即可.
【解答】解:根据旋转的性质,可知MN从原先的位置转到MN⊥AB,要经过30°或180°+30°=210°,
∴30÷3=10(秒);210÷3=70(秒),
故答案为:10或70.
【点评】本题考查了角的计算,解题的关键是读懂题意,掌握旋转中角的变化.
10.(2024秋 镇平县期末)如图所示的网格是正方形网格,∠DEF < ∠ABC.(填“>”,“=”或“<”)
【考点】角的大小比较.
【专题】几何直观.
【答案】<.
【分析】过点E向下作竖直线EG,根据网格线可得∠ABC=∠DEG,∠EDG>∠DEF,即可比较∠DEF和∠ABC的大小.
【解答】解:过点E向下作竖直线EG,
由网格线可得,∠ABC=∠DEG=45°,
∵∠EDG>∠DEF,
∴∠DEF<∠ABC,
故答案为:<.
【点评】本题主要考查角的大小比较,利用网格线得出∠ABC=∠DEG=45°是解题的关键.
三.解答题(共5小题)
11.(2024秋 临洮县期中)如图,B岛在A岛的南偏西40°方向,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东80°方向,求从C岛看A,B两岛的视角∠ACB的度数.
【考点】方向角.
【专题】线段、角、相交线与平行线;几何直观.
【答案】85°.
【分析】由题意得:BE∥AD,∠BAD=40°,∠CAD=15°,∠EBC=80°,再根据平行线的性质以及三角形内角和定理,即可得到∠ACB的度数.
【解答】解:如图,由题意得:BE∥AD,∠BAD=40°,∠CAD=15°,∠EBC=80°,
∴∠EBA=∠BAD=40°,
∴∠BAC=∠BAD+∠CAD=40°+15°=55°,
∴∠CBA=∠EBC﹣∠EBA=80°﹣40°=40°,
∴∠ACB=180°﹣∠BAC﹣∠ABC
=180°﹣55°﹣40°=85°,
答:从C岛看A,B两岛的视角∠ACB的度数为85°.
【点评】本题主要考查了方向角,方向角是表示方向的角;以正北,正南方向为基准,来描述物体所处的方向.
12.(2024秋 杜尔伯特县期末)如图,已知∠AOB=120°,OC是∠AOB内的一条射线,且∠AOC:∠BOC=1:2.
(1)求∠AOC的度数;
(2)过点O作射线OD,若∠AOD∠AOB,求∠COD的度数.
【考点】角的计算.
【专题】线段、角、相交线与平行线;运算能力.
【答案】见试题解答内容
【分析】(1)根据∠AOC:∠BOC=1:2,即可求解;
(2)先求出∠COM,再求出∠CON,相加即可求解.
【解答】解:(1)∵∠AOC:∠BOC=1:2,∠AOB=120°,
∴∠AOC∠AOB120°=40°;
(2)∵∠AOD∠AOB,
∴∠AOD=60°,
当OD在∠AOB内时,
∠COD=∠AOD﹣∠AOC=20°,
当OD在∠AOB外时,
∠COD=∠AOC+∠AOD=100°.
故∠COD的度数为20°或100°.
【点评】本题考查了角的计算及角平分线,掌握角的特点及比例的意义是解决问题的关键.
13.(2024秋 凉山州期末)如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
【考点】角的计算.
【专题】计算题.
【答案】见试题解答内容
【分析】(1)根据角平分线定义得到∠AOC∠EOC70°=35°,然后根据对顶角相等得到∠BOD=∠AOC=35°;
(2)先设∠EOC=2x,∠EOD=3x,根据平角的定义得2x+3x=180°,解得x=36°,则∠EOC=2x=72°,然后与(1)的计算方法一样.
【解答】解:(1)∵OA平分∠EOC,
∴∠AOC∠EOC70°=35°,
∴∠BOD=∠AOC=35°;
(2)设∠EOC=2x,∠EOD=3x,根据题意得2x+3x=180°,解得x=36°,
∴∠EOC=2x=72°,
∴∠AOC∠EOC72°=36°,
∴∠BOD=∠AOC=36°.
【点评】考查了角的计算:1直角=90°;1平角=180°.也考查了角平分线的定义和对顶角的性质.
14.(2024春 阳谷县期末)如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
(1)射线OC的方向是 北偏东70° ;
(2)求∠COD的度数;
(3)若射线OE平分∠COD,求∠AOE的度数.
【考点】方向角.
【答案】见试题解答内容
【分析】(1)先求出∠AOB=55°,再求得∠NOC的度数,即可确定OC的方向;
(2)根据∠AOB=55°,∠AOC=∠AOB,得出∠BOC=110°,进而求出∠COD的度数;
(3)根据射线OE平分∠COD,即可求出∠COE=35°再利用∠AOC=55°求出答案即可.
【解答】解:(1)∵OB的方向是北偏西40°,OA的方向是北偏东15°,
∴∠NOB=40°,∠NOA=15°,
∴∠AOB=∠NOB+∠NOA=55°,
∵∠AOB=∠AOC,
∴∠AOC=55°,
∴∠NOC=∠NOA+∠AOC=70°,
∴OC的方向是北偏东70°;
故答案为:北偏东70°;
(2)∵∠AOB=55°,∠AOC=∠AOB,
∴∠BOC=110°.
又∵射线OD是OB的反向延长线,
∴∠BOD=180°.
∴∠COD=180°﹣110°=70°.
(3)∵∠COD=70°,OE平分∠COD,
∴∠COE=35°.
∵∠AOC=55°.
∴∠AOE=90°.
【点评】此题主要考查了方向角的表达即方向角一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)多少度.
15.(2024秋 丰润区期末)【实践活动】
如图1,将一副三角板的直角顶点重合摆放.
(1)∠ACE与∠BCD的大小关系是∠ACE = ∠BCD.(填“>”“=”或“<”)
(2)∠ACB与∠DCE之间的数量关系是 ∠ACB+∠DCE=180° .
【拓展探究】
(3)如图2,若∠ACD≠∠BCE,且∠ACD+∠BCE=180°,探索∠ACB与∠DCE之间的数量关系,并说明理由.
【考点】角的大小比较;角的计算.
【专题】线段、角、相交线与平行线;几何直观;运算能力;推理能力.
【答案】(1)=;
(2)∠ACB+∠DCE=180°,理由见解答过程;
(3)∠ACB+∠DCE=180°,理由见解答过程.
【分析】(1)依题意得∠ACD=90°,∠ECB=90°,进而得∠ACE+∠DCE=90°,∠DCE+∠BCD=90°,然后根据同角的余角相等可得出答案;
(2)由∠ACD=90°,∠ECB=90°得∠ACE+∠DCE=90°,∠DCE+∠BCD=90°,则∠ACE+2∠DCE+∠BCD=180°,然而∠ACB+∠DCE=∠ACE+2∠DCE+∠BCD=180°;据此可得∠ACB与∠DCE之间的数量关系;
(3)先由∠ACD+∠BCE=180°得∠ACE+2∠DCE+∠BCD=180°,进而得∠ACB+∠DCE=∠ACE+2∠DCE+∠BCD=180°,据此可得∠ACB与∠DCE之间的数量关系.
【解答】解:(1)依题意得:∠ACD=90°,∠ECB=90°,
∴∠ACE+∠DCE=90°,∠DCE+∠BCD=90°,
∴∠ACE=∠BCD.
故答案为:=.
(2)∠ACB与∠DCE之间的数量关系:∠ACB+∠DCE=180°,理由如下:
∵∠ACD=90°,∠ECB=90°,
∴∠ACE+∠DCE=90°,∠DCE+∠BCD=90°,
∵∠ACE+∠DCE+∠DCE+∠BCD=90°+90°,
∴∠ACE+2∠DCE+∠BCD=180°,
又∵∠ACB=∠ACE+∠DCE+∠BCD,
∴∠ACB+∠DCE=∠ACE+∠DCE+∠BCD+∠DCE=∠ACE+2∠DCE+∠BCD=180°;
(3)∠ACB与∠DCE之间的数量关系是:∠ACB+∠DCE=180°,理由如下:
∵∠ACD=∠ACE+∠DCE,∠BCE=∠DCE+∠BCD,
又∵∠ACD+∠BCE=180°,
∴∠ACE+∠DCE+∠DCE+∠BCD=180°,
即:∠ACE+2∠DCE+∠BCD=180°,
∴∠ACB+∠DCE=∠ACE+∠DCE+∠BCD+∠DCE=∠ACE+2∠DCE+∠BCD=180°.
【点评】此题主要考查了角的计算,同角的余角相等,准确识图,理解同角的余角相等,熟练掌握角的计算是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
