4.3多边形和圆的初步认识(预习衔接.夯实基础.含解析)-2025-2026学年七年级上册数学北师大版(2024)
文档属性
| 名称 | 4.3多边形和圆的初步认识(预习衔接.夯实基础.含解析)-2025-2026学年七年级上册数学北师大版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 401.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 20:42:39 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
预习衔接.夯实基础 多边形和圆的初步认识
一.选择题(共5小题)
1.(2024 桥西区校级三模)如图是被撕掉一块的正多边形纸片,若直线a⊥b,则该正多边形是( )
A.正五边形 B.正六边形 C.正八边形 D.正十边形
2.(2024秋 和静县校级期中)一个多边形自一个顶点引对角线把它分割为六个三角形,那么它是( )
A.六边形 B.七边形 C.八边形 D.九边形
3.(2024秋 永善县期末)已知⊙O中最长的弦为8,则⊙O的半径是( )
A.4 B.8 C.12 D.16
4.(2024秋 赣县区期末)
如图是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角∠O=120°形成的扇面,若OA=5m,OB=3m,则阴影部分的面积是( )
A. B. C.4π D.
5.(2024春 淮安区期末)若一个多边形从一个顶点最多能引出5条对角线,则这个多边形是( )
A.六边形 B.八边形 C.九边形 D.十边形
二.填空题(共5小题)
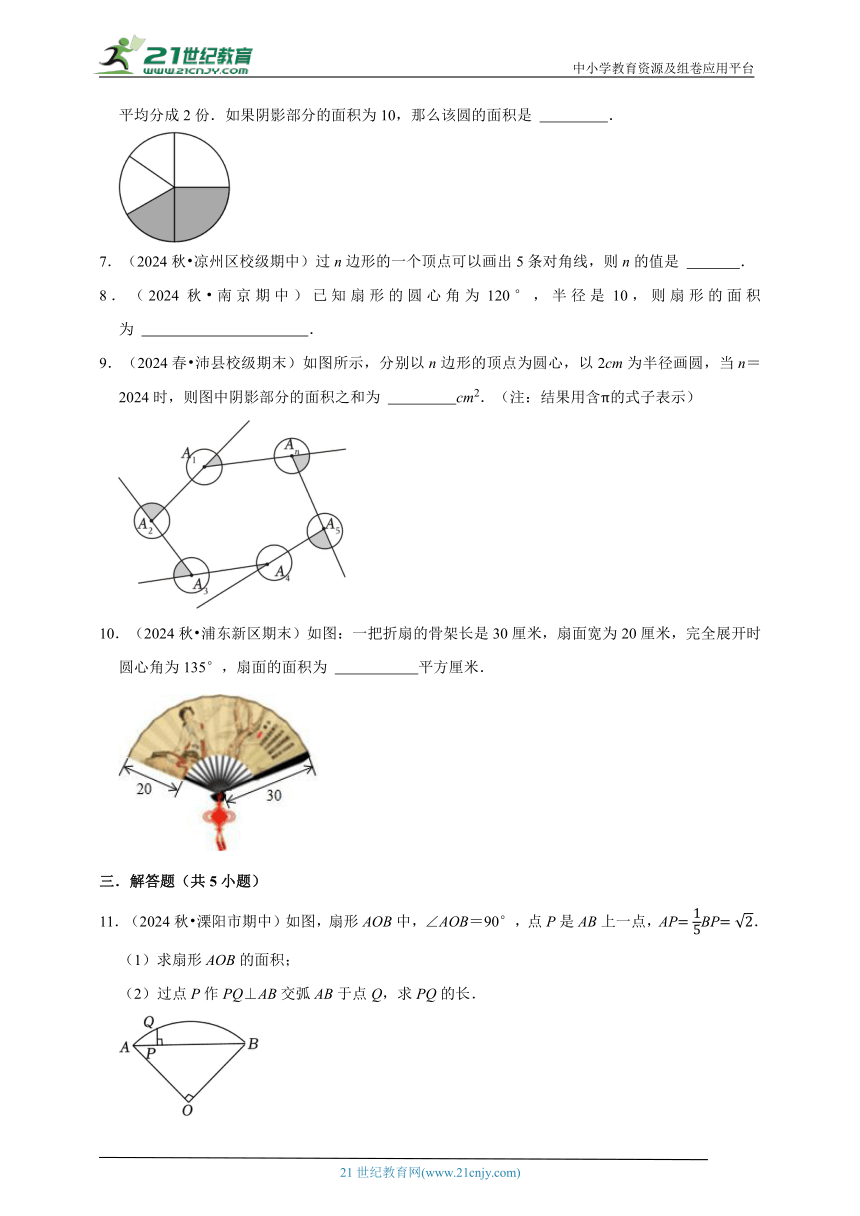
6.(2024秋 宝山区期中)如图,把一个圆平均分成两个半圆,再把左半圆平均分成3份,右半圆平均分成2份.如果阴影部分的面积为10,那么该圆的面积是 .
7.(2024秋 凉州区校级期中)过n边形的一个顶点可以画出5条对角线,则n的值是 .
8.(2024秋 南京期中)已知扇形的圆心角为120°,半径是10,则扇形的面积为 .
9.(2024春 沛县校级期末)如图所示,分别以n边形的顶点为圆心,以2cm为半径画圆,当n=2024时,则图中阴影部分的面积之和为 cm2.(注:结果用含π的式子表示)
10.(2024秋 浦东新区期末)如图:一把折扇的骨架长是30厘米,扇面宽为20厘米,完全展开时圆心角为135°,扇面的面积为 平方厘米.
三.解答题(共5小题)
11.(2024秋 溧阳市期中)如图,扇形AOB中,∠AOB=90°,点P是AB上一点,APBP.
(1)求扇形AOB的面积;
(2)过点P作PQ⊥AB交弧AB于点Q,求PQ的长.
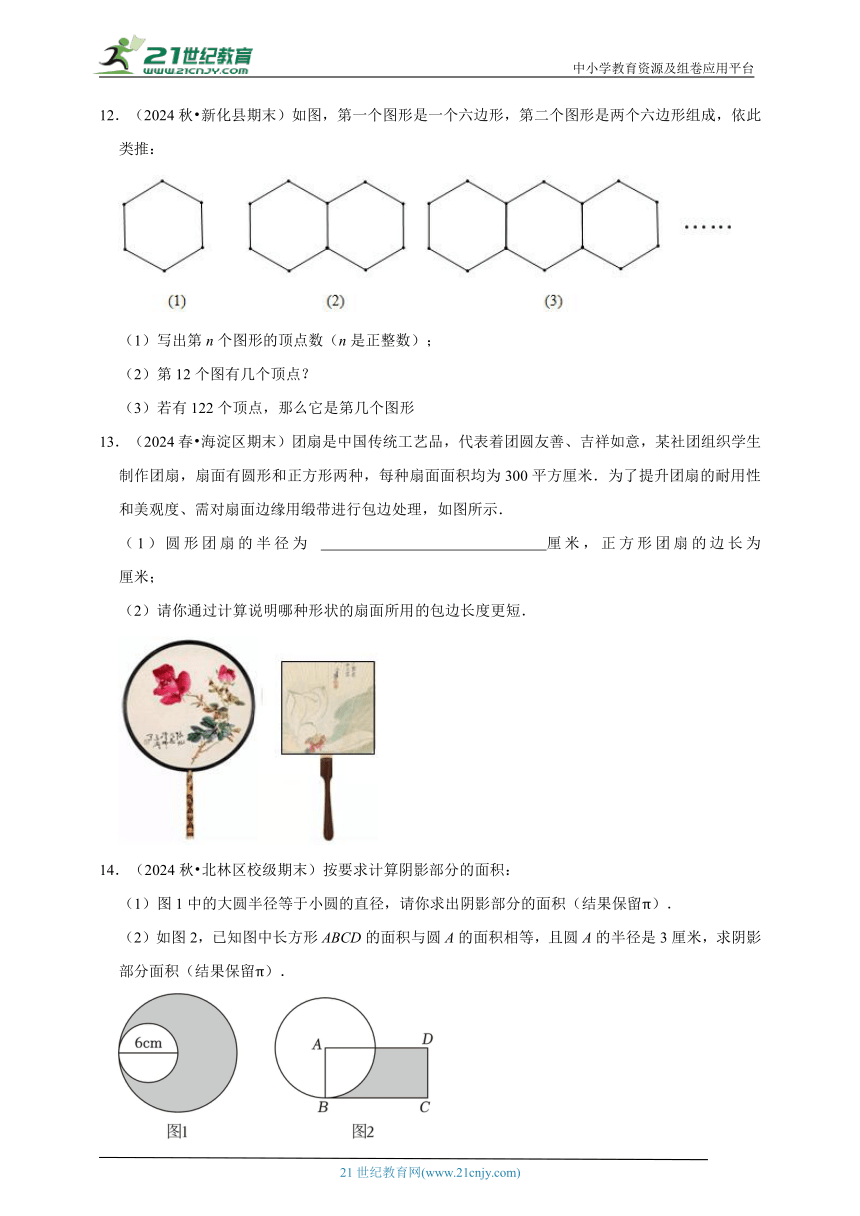
12.(2024秋 新化县期末)如图,第一个图形是一个六边形,第二个图形是两个六边形组成,依此类推:
(1)写出第n个图形的顶点数(n是正整数);
(2)第12个图有几个顶点?
(3)若有122个顶点,那么它是第几个图形
13.(2024春 海淀区期末)团扇是中国传统工艺品,代表着团圆友善、吉祥如意,某社团组织学生制作团扇,扇面有圆形和正方形两种,每种扇面面积均为300平方厘米.为了提升团扇的耐用性和美观度、需对扇面边缘用缎带进行包边处理,如图所示.
(1)圆形团扇的半径为 厘米,正方形团扇的边长为 厘米;
(2)请你通过计算说明哪种形状的扇面所用的包边长度更短.
14.(2024秋 北林区校级期末)按要求计算阴影部分的面积:
(1)图1中的大圆半径等于小圆的直径,请你求出阴影部分的面积(结果保留π).
(2)如图2,已知图中长方形ABCD的面积与圆A的面积相等,且圆A的半径是3厘米,求阴影部分面积(结果保留π).
15.(2024秋 浦东新区期末)如图,下面的爱心图案是由一个正方形和两个半圆组成,其中正方形的边长为20,请计算图中阴影部分的面积是多少?(π取3.14)
预习衔接.夯实基础 多边形和圆的初步认识
参考答案与试题解析
一.选择题(共5小题)
1.(2024 桥西区校级三模)如图是被撕掉一块的正多边形纸片,若直线a⊥b,则该正多边形是( )
A.正五边形 B.正六边形 C.正八边形 D.正十边形
【考点】多边形.
【专题】多边形与平行四边形;运算能力.
【答案】C
【分析】先延长DA,EB交于点C,再根据已知条件求出∠C,然后根据正多边形的定义求出∠DAB=∠ABE,从而根据邻补角定义求出正多边形的一个外角,最后根据多边形外角和求出边数即可.
【解答】解:如图所示:延长DA,EB交于点C,
∵直线a⊥b,
∴∠C=90°,
∵此多边形是正多边形,
∴∠DAB=∠ABE,
∴∠CAB=∠CBA=45°,
∵正多边形外角和为360°,
∴正多边形的边数为360°÷45°=8,
故选:C.
【点评】本题主要考查了正多边形的定义,解题关键是添加辅助线构造三角形.
2.(2024秋 和静县校级期中)一个多边形自一个顶点引对角线把它分割为六个三角形,那么它是( )
A.六边形 B.七边形 C.八边形 D.九边形
【考点】多边形的对角线.
【答案】C
【分析】根据n边形过一个顶点有(n﹣3)条对角线,它们把n边形分割成了(n﹣2)个三角形.
【解答】解:设多边形有n条边,
则n﹣2=6,n=8,
故多边形是八边形.
故选:C.
【点评】此题主要考查了多边形的对角线,熟悉多边形中的公式:n边形过一个顶点有(n﹣3)条对角线,它们把n边形分割成了(n﹣2)个三角形.
3.(2024秋 永善县期末)已知⊙O中最长的弦为8,则⊙O的半径是( )
A.4 B.8 C.12 D.16
【考点】圆的认识.
【专题】与圆有关的计算;运算能力.
【答案】A
【分析】⊙O最长的弦就是直径从而不难求得半径的长.
【解答】解:∵⊙O中最长的弦为8,即直径为8,
∴⊙O的半径为4.
故选:A.
【点评】本题考查弦,直径等知识,记住圆中的最长的弦就是直径是解题的关键.
4.(2024秋 赣县区期末)
如图是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角∠O=120°形成的扇面,若OA=5m,OB=3m,则阴影部分的面积是( )
A. B. C.4π D.
【考点】扇形面积的计算.
【专题】与圆有关的计算;运算能力.
【答案】D
【分析】利用扇形面积公式,根据S阴影=S扇形AOD﹣S扇形BOC即可求解.
【解答】解:S阴影=S扇形AOD﹣S扇形BOC
(m2),
故选:D.
【点评】本题考查了求扇形面积,熟练掌握扇形面积公式是解题的关键.
5.(2024春 淮安区期末)若一个多边形从一个顶点最多能引出5条对角线,则这个多边形是( )
A.六边形 B.八边形 C.九边形 D.十边形
【考点】多边形的对角线;多边形.
【专题】多边形与平行四边形;几何直观.
【答案】B
【分析】根据从n边形的一个顶点可以作对角线的条数公式(n﹣3)求出边数即可得解.
【解答】解:∵从一个多边形的一个顶点出发可以引5条对角线,设多边形边数为n,
∴n﹣3=5,
解得n=8.
故选:B.
【点评】本题考查了多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.掌握n边形从一个顶点出发可引出(n﹣3)条对角线是解题的关键.
二.填空题(共5小题)
6.(2024秋 宝山区期中)如图,把一个圆平均分成两个半圆,再把左半圆平均分成3份,右半圆平均分成2份.如果阴影部分的面积为10,那么该圆的面积是 24 .
【考点】扇形面积的计算.
【专题】运算能力.
【答案】24.
【分析】根据所给阴影部分的面积,得出圆的半径,据此可解决问题.
【解答】解:由题知,
180°÷3=60°,180°÷2=90°,
则60°+90°=150°,
所以图中阴影部分扇形的圆心角度数为150°.
设圆的半径为r,
则,
所以r2,
则圆的面积为:.
故答案为:24.
【点评】本题主要考查了扇形面积的计算,熟知扇形的面积公式是解题的关键.
7.(2024秋 凉州区校级期中)过n边形的一个顶点可以画出5条对角线,则n的值是 8 .
【考点】多边形的对角线.
【专题】多边形与平行四边形;运算能力.
【答案】8.
【分析】由过n边形的一个顶点可以画出(n﹣3)条对角线,根据题意,得n﹣3=5,解答即可.
【解答】解:根据题意得:n﹣3=5,
解得:n=8,
故答案为:8.
【点评】本题考查了多边形的性质,解方程,熟练掌握性质,灵活解方程是解题的关键.
8.(2024秋 南京期中)已知扇形的圆心角为120°,半径是10,则扇形的面积为 .
【考点】扇形面积的计算.
【专题】与圆有关的计算;运算能力.
【答案】.
【分析】根据扇形面积的计算方法进行计算即可.
【解答】解:扇形的圆心角为120°,半径是10,则扇形的面积为,
故答案为:.
【点评】本题考查扇形面积的计算,掌握扇形面积的计算方法是正确解答的关键.
9.(2024春 沛县校级期末)如图所示,分别以n边形的顶点为圆心,以2cm为半径画圆,当n=2024时,则图中阴影部分的面积之和为 4π cm2.(注:结果用含π的式子表示)
【考点】扇形面积的计算.
【专题】圆的有关概念及性质;运算能力.
【答案】4π.
【分析】由题意得到各顶点的扇形圆心角之和即为n边形外角和,利用扇形面积公式计算即可求出阴影部分面积.
【解答】解:∵n边形的外角和为360°,半径为2cm,
∴S阴影4πcm2,
故答案为:4π.
【点评】此题考查了扇形面积的计算,以及多边形的内角和与外角和,熟练掌握扇形面积公式是解本题的关键.
10.(2024秋 浦东新区期末)如图:一把折扇的骨架长是30厘米,扇面宽为20厘米,完全展开时圆心角为135°,扇面的面积为 300π 平方厘米.
【考点】扇形面积的计算.
【专题】圆的有关概念及性质;运算能力.
【答案】300π.
【分析】利用扇形的面积公式代入数据计算即可解答问题.
【解答】解:30﹣20=10(厘米)
=300π(平方厘米),
扇面的面积是300π平方厘米,
故答案为:300π.
【点评】此题考查了扇形的面积公式的实际应用,熟记公式即可解答问题.
三.解答题(共5小题)
11.(2024秋 溧阳市期中)如图,扇形AOB中,∠AOB=90°,点P是AB上一点,APBP.
(1)求扇形AOB的面积;
(2)过点P作PQ⊥AB交弧AB于点Q,求PQ的长.
【考点】扇形面积的计算.
【专题】与圆有关的计算;运算能力.
【答案】(1)9π;
(2).
【分析】(1)依题意得AB,OA=OB,∠AOB=90°,则△OAB是等腰直角三角形,再由勾股定理求出OA=6,进而可得扇形AOB的面积;
(2)过O作OC⊥AB于C,OD⊥PQ交QP的延长线于D,QD交OA于E,证明四边形OCPD为矩形,再根据△OAB是等腰直角三角形得AC=BC=OC,OQ=OA=6,则OD=PC,PD=OC,然后由勾股定理求出DQ,进而可得PQ的长.
【解答】解:(1)∵APBP,
∴AP,BP,
∴AB=AP+BP,
∵OA=OB,∠AOB=90°,
∴△OAB是等腰直角三角形,
由勾股定理得:AB,
∴,
∴OA=6,
∴扇形AOB的面积为:9π;
(2)过点O作OC⊥AB于C,作OD⊥PQ交QP的延长线于D,QD交OA于点E,连接OQ,如图所示:
∵PQ⊥AB,
∴四边形OCPD为矩形,
∴OC=DP,OD=PC,
由(1)知:△OAB是等腰直角三角形,且OA=OB=6,AB,AP,
∴AC=BC=OCAB,OQ=OA=6,
∴OD=PC=AC﹣AP,PD=OC,
在Rt△ODQ中,由勾股定理得:DQ,
∴PQ=DQ﹣PD.
【点评】此题主要考查了扇形面积,熟练掌握扇形的面积公式是解决问题的关键.
12.(2024秋 新化县期末)如图,第一个图形是一个六边形,第二个图形是两个六边形组成,依此类推:
(1)写出第n个图形的顶点数(n是正整数);
(2)第12个图有几个顶点?
(3)若有122个顶点,那么它是第几个图形
【考点】多边形;列代数式;代数式求值;规律型:图形的变化类.
【专题】规律型;一次方程(组)及应用;推理能力.
【答案】见试题解答内容
【分析】(1)由第1个图形的顶点数为4+2,第2个图形的顶点数为2×4+2,第3个图形的顶点数为3×4+2,…,得出第n个图形的顶点数为4n+2;
(2)将12代入4n+2,即可得出结果;
(3)由4n+2=122,即可得出结果.
【解答】解:(1)第1个图形的顶点数为:4+2,
第2个图形的顶点数为:2×4+2,
第3个图形的顶点数为:3×4+2,
…,
第n个图形的顶点数为:n×4+2=4n+2;
(2)第12个图的顶点数为:4×12+2=50,
∴第12个图有50个顶点;
(3)4n+2=122,
解得:n=30,
∴若有122个顶点,那么它是第30个图形.
【点评】本题考查了图形的变化规律、解一元一次方程等知识;认真观察得出规律是解题的关键.
13.(2024春 海淀区期末)团扇是中国传统工艺品,代表着团圆友善、吉祥如意,某社团组织学生制作团扇,扇面有圆形和正方形两种,每种扇面面积均为300平方厘米.为了提升团扇的耐用性和美观度、需对扇面边缘用缎带进行包边处理,如图所示.
(1)圆形团扇的半径为 厘米,正方形团扇的边长为 厘米;
(2)请你通过计算说明哪种形状的扇面所用的包边长度更短.
【考点】扇形面积的计算.
【专题】与圆有关的计算;运算能力.
【答案】(1),;
(2)圆形团扇所用的包边长度更短.
【分析】(1)分别根据圆和正方形的面积公式解答即可;
(2)根据圆和正方形的周长公式解答即可.
【解答】解:(1)由题意得:
圆形团扇的半径为:(厘米),正方形团扇的边长为:(厘米),
故答案为:,;
(2)∵圆形团扇的半径为厘米,
∴圆形团扇的周长为:(厘米),
∵正方形团扇的边长为厘米,
∴正方形团扇的周长为:(厘米),
∵,3<π<4,
∴,
∴圆形团扇所用的包边长度更短.
【点评】本题考查了扇形的面积,掌握圆和正方形的面积和周长公式是解答本题的关键.
14.(2024秋 北林区校级期末)按要求计算阴影部分的面积:
(1)图1中的大圆半径等于小圆的直径,请你求出阴影部分的面积(结果保留π).
(2)如图2,已知图中长方形ABCD的面积与圆A的面积相等,且圆A的半径是3厘米,求阴影部分面积(结果保留π).
【考点】扇形面积的计算.
【专题】与圆有关的计算;运算能力.
【答案】(1)27π平方厘米;
(2)是 平方厘米.
【分析】(1)用大圆面积减去小圆面积即可;
(2)用长方形的面积减去扇形面积即可.
【解答】解:(1)π×62﹣π×()2
=36π﹣9π
=27π(平方厘米),
答:阴影部分的面积是27π平方厘米;
(2)∵长方形面积与圆面积相等,扇形的圆心角为90°,
∴S阴影部分=S矩形﹣S扇形
=S圆﹣S扇形
S圆
(平方厘米),
答:阴影部分的面积是 平方厘米.
【点评】本题考查扇形面积的计算,掌握扇形面积的计算方法是正确解答的关键.
15.(2024秋 浦东新区期末)如图,下面的爱心图案是由一个正方形和两个半圆组成,其中正方形的边长为20,请计算图中阴影部分的面积是多少?(π取3.14)
【考点】扇形面积的计算.
【专题】与圆有关的计算;运算能力.
【答案】400.
【分析】根据阴影的面积等于正方形面积减去扇形ABC的面积再加上一个圆的面积,计算即可.
【解答】解:202π×102=400﹣100π+100π=400,
答:阴影部分的面积是400.
【点评】本题考查了扇形面积的计算,关键是熟记扇形的面积公式和准确计算.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.夯实基础 多边形和圆的初步认识
一.选择题(共5小题)
1.(2024 桥西区校级三模)如图是被撕掉一块的正多边形纸片,若直线a⊥b,则该正多边形是( )
A.正五边形 B.正六边形 C.正八边形 D.正十边形
2.(2024秋 和静县校级期中)一个多边形自一个顶点引对角线把它分割为六个三角形,那么它是( )
A.六边形 B.七边形 C.八边形 D.九边形
3.(2024秋 永善县期末)已知⊙O中最长的弦为8,则⊙O的半径是( )
A.4 B.8 C.12 D.16
4.(2024秋 赣县区期末)
如图是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角∠O=120°形成的扇面,若OA=5m,OB=3m,则阴影部分的面积是( )
A. B. C.4π D.
5.(2024春 淮安区期末)若一个多边形从一个顶点最多能引出5条对角线,则这个多边形是( )
A.六边形 B.八边形 C.九边形 D.十边形
二.填空题(共5小题)
6.(2024秋 宝山区期中)如图,把一个圆平均分成两个半圆,再把左半圆平均分成3份,右半圆平均分成2份.如果阴影部分的面积为10,那么该圆的面积是 .
7.(2024秋 凉州区校级期中)过n边形的一个顶点可以画出5条对角线,则n的值是 .
8.(2024秋 南京期中)已知扇形的圆心角为120°,半径是10,则扇形的面积为 .
9.(2024春 沛县校级期末)如图所示,分别以n边形的顶点为圆心,以2cm为半径画圆,当n=2024时,则图中阴影部分的面积之和为 cm2.(注:结果用含π的式子表示)
10.(2024秋 浦东新区期末)如图:一把折扇的骨架长是30厘米,扇面宽为20厘米,完全展开时圆心角为135°,扇面的面积为 平方厘米.
三.解答题(共5小题)
11.(2024秋 溧阳市期中)如图,扇形AOB中,∠AOB=90°,点P是AB上一点,APBP.
(1)求扇形AOB的面积;
(2)过点P作PQ⊥AB交弧AB于点Q,求PQ的长.
12.(2024秋 新化县期末)如图,第一个图形是一个六边形,第二个图形是两个六边形组成,依此类推:
(1)写出第n个图形的顶点数(n是正整数);
(2)第12个图有几个顶点?
(3)若有122个顶点,那么它是第几个图形
13.(2024春 海淀区期末)团扇是中国传统工艺品,代表着团圆友善、吉祥如意,某社团组织学生制作团扇,扇面有圆形和正方形两种,每种扇面面积均为300平方厘米.为了提升团扇的耐用性和美观度、需对扇面边缘用缎带进行包边处理,如图所示.
(1)圆形团扇的半径为 厘米,正方形团扇的边长为 厘米;
(2)请你通过计算说明哪种形状的扇面所用的包边长度更短.
14.(2024秋 北林区校级期末)按要求计算阴影部分的面积:
(1)图1中的大圆半径等于小圆的直径,请你求出阴影部分的面积(结果保留π).
(2)如图2,已知图中长方形ABCD的面积与圆A的面积相等,且圆A的半径是3厘米,求阴影部分面积(结果保留π).
15.(2024秋 浦东新区期末)如图,下面的爱心图案是由一个正方形和两个半圆组成,其中正方形的边长为20,请计算图中阴影部分的面积是多少?(π取3.14)
预习衔接.夯实基础 多边形和圆的初步认识
参考答案与试题解析
一.选择题(共5小题)
1.(2024 桥西区校级三模)如图是被撕掉一块的正多边形纸片,若直线a⊥b,则该正多边形是( )
A.正五边形 B.正六边形 C.正八边形 D.正十边形
【考点】多边形.
【专题】多边形与平行四边形;运算能力.
【答案】C
【分析】先延长DA,EB交于点C,再根据已知条件求出∠C,然后根据正多边形的定义求出∠DAB=∠ABE,从而根据邻补角定义求出正多边形的一个外角,最后根据多边形外角和求出边数即可.
【解答】解:如图所示:延长DA,EB交于点C,
∵直线a⊥b,
∴∠C=90°,
∵此多边形是正多边形,
∴∠DAB=∠ABE,
∴∠CAB=∠CBA=45°,
∵正多边形外角和为360°,
∴正多边形的边数为360°÷45°=8,
故选:C.
【点评】本题主要考查了正多边形的定义,解题关键是添加辅助线构造三角形.
2.(2024秋 和静县校级期中)一个多边形自一个顶点引对角线把它分割为六个三角形,那么它是( )
A.六边形 B.七边形 C.八边形 D.九边形
【考点】多边形的对角线.
【答案】C
【分析】根据n边形过一个顶点有(n﹣3)条对角线,它们把n边形分割成了(n﹣2)个三角形.
【解答】解:设多边形有n条边,
则n﹣2=6,n=8,
故多边形是八边形.
故选:C.
【点评】此题主要考查了多边形的对角线,熟悉多边形中的公式:n边形过一个顶点有(n﹣3)条对角线,它们把n边形分割成了(n﹣2)个三角形.
3.(2024秋 永善县期末)已知⊙O中最长的弦为8,则⊙O的半径是( )
A.4 B.8 C.12 D.16
【考点】圆的认识.
【专题】与圆有关的计算;运算能力.
【答案】A
【分析】⊙O最长的弦就是直径从而不难求得半径的长.
【解答】解:∵⊙O中最长的弦为8,即直径为8,
∴⊙O的半径为4.
故选:A.
【点评】本题考查弦,直径等知识,记住圆中的最长的弦就是直径是解题的关键.
4.(2024秋 赣县区期末)
如图是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角∠O=120°形成的扇面,若OA=5m,OB=3m,则阴影部分的面积是( )
A. B. C.4π D.
【考点】扇形面积的计算.
【专题】与圆有关的计算;运算能力.
【答案】D
【分析】利用扇形面积公式,根据S阴影=S扇形AOD﹣S扇形BOC即可求解.
【解答】解:S阴影=S扇形AOD﹣S扇形BOC
(m2),
故选:D.
【点评】本题考查了求扇形面积,熟练掌握扇形面积公式是解题的关键.
5.(2024春 淮安区期末)若一个多边形从一个顶点最多能引出5条对角线,则这个多边形是( )
A.六边形 B.八边形 C.九边形 D.十边形
【考点】多边形的对角线;多边形.
【专题】多边形与平行四边形;几何直观.
【答案】B
【分析】根据从n边形的一个顶点可以作对角线的条数公式(n﹣3)求出边数即可得解.
【解答】解:∵从一个多边形的一个顶点出发可以引5条对角线,设多边形边数为n,
∴n﹣3=5,
解得n=8.
故选:B.
【点评】本题考查了多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.掌握n边形从一个顶点出发可引出(n﹣3)条对角线是解题的关键.
二.填空题(共5小题)
6.(2024秋 宝山区期中)如图,把一个圆平均分成两个半圆,再把左半圆平均分成3份,右半圆平均分成2份.如果阴影部分的面积为10,那么该圆的面积是 24 .
【考点】扇形面积的计算.
【专题】运算能力.
【答案】24.
【分析】根据所给阴影部分的面积,得出圆的半径,据此可解决问题.
【解答】解:由题知,
180°÷3=60°,180°÷2=90°,
则60°+90°=150°,
所以图中阴影部分扇形的圆心角度数为150°.
设圆的半径为r,
则,
所以r2,
则圆的面积为:.
故答案为:24.
【点评】本题主要考查了扇形面积的计算,熟知扇形的面积公式是解题的关键.
7.(2024秋 凉州区校级期中)过n边形的一个顶点可以画出5条对角线,则n的值是 8 .
【考点】多边形的对角线.
【专题】多边形与平行四边形;运算能力.
【答案】8.
【分析】由过n边形的一个顶点可以画出(n﹣3)条对角线,根据题意,得n﹣3=5,解答即可.
【解答】解:根据题意得:n﹣3=5,
解得:n=8,
故答案为:8.
【点评】本题考查了多边形的性质,解方程,熟练掌握性质,灵活解方程是解题的关键.
8.(2024秋 南京期中)已知扇形的圆心角为120°,半径是10,则扇形的面积为 .
【考点】扇形面积的计算.
【专题】与圆有关的计算;运算能力.
【答案】.
【分析】根据扇形面积的计算方法进行计算即可.
【解答】解:扇形的圆心角为120°,半径是10,则扇形的面积为,
故答案为:.
【点评】本题考查扇形面积的计算,掌握扇形面积的计算方法是正确解答的关键.
9.(2024春 沛县校级期末)如图所示,分别以n边形的顶点为圆心,以2cm为半径画圆,当n=2024时,则图中阴影部分的面积之和为 4π cm2.(注:结果用含π的式子表示)
【考点】扇形面积的计算.
【专题】圆的有关概念及性质;运算能力.
【答案】4π.
【分析】由题意得到各顶点的扇形圆心角之和即为n边形外角和,利用扇形面积公式计算即可求出阴影部分面积.
【解答】解:∵n边形的外角和为360°,半径为2cm,
∴S阴影4πcm2,
故答案为:4π.
【点评】此题考查了扇形面积的计算,以及多边形的内角和与外角和,熟练掌握扇形面积公式是解本题的关键.
10.(2024秋 浦东新区期末)如图:一把折扇的骨架长是30厘米,扇面宽为20厘米,完全展开时圆心角为135°,扇面的面积为 300π 平方厘米.
【考点】扇形面积的计算.
【专题】圆的有关概念及性质;运算能力.
【答案】300π.
【分析】利用扇形的面积公式代入数据计算即可解答问题.
【解答】解:30﹣20=10(厘米)
=300π(平方厘米),
扇面的面积是300π平方厘米,
故答案为:300π.
【点评】此题考查了扇形的面积公式的实际应用,熟记公式即可解答问题.
三.解答题(共5小题)
11.(2024秋 溧阳市期中)如图,扇形AOB中,∠AOB=90°,点P是AB上一点,APBP.
(1)求扇形AOB的面积;
(2)过点P作PQ⊥AB交弧AB于点Q,求PQ的长.
【考点】扇形面积的计算.
【专题】与圆有关的计算;运算能力.
【答案】(1)9π;
(2).
【分析】(1)依题意得AB,OA=OB,∠AOB=90°,则△OAB是等腰直角三角形,再由勾股定理求出OA=6,进而可得扇形AOB的面积;
(2)过O作OC⊥AB于C,OD⊥PQ交QP的延长线于D,QD交OA于E,证明四边形OCPD为矩形,再根据△OAB是等腰直角三角形得AC=BC=OC,OQ=OA=6,则OD=PC,PD=OC,然后由勾股定理求出DQ,进而可得PQ的长.
【解答】解:(1)∵APBP,
∴AP,BP,
∴AB=AP+BP,
∵OA=OB,∠AOB=90°,
∴△OAB是等腰直角三角形,
由勾股定理得:AB,
∴,
∴OA=6,
∴扇形AOB的面积为:9π;
(2)过点O作OC⊥AB于C,作OD⊥PQ交QP的延长线于D,QD交OA于点E,连接OQ,如图所示:
∵PQ⊥AB,
∴四边形OCPD为矩形,
∴OC=DP,OD=PC,
由(1)知:△OAB是等腰直角三角形,且OA=OB=6,AB,AP,
∴AC=BC=OCAB,OQ=OA=6,
∴OD=PC=AC﹣AP,PD=OC,
在Rt△ODQ中,由勾股定理得:DQ,
∴PQ=DQ﹣PD.
【点评】此题主要考查了扇形面积,熟练掌握扇形的面积公式是解决问题的关键.
12.(2024秋 新化县期末)如图,第一个图形是一个六边形,第二个图形是两个六边形组成,依此类推:
(1)写出第n个图形的顶点数(n是正整数);
(2)第12个图有几个顶点?
(3)若有122个顶点,那么它是第几个图形
【考点】多边形;列代数式;代数式求值;规律型:图形的变化类.
【专题】规律型;一次方程(组)及应用;推理能力.
【答案】见试题解答内容
【分析】(1)由第1个图形的顶点数为4+2,第2个图形的顶点数为2×4+2,第3个图形的顶点数为3×4+2,…,得出第n个图形的顶点数为4n+2;
(2)将12代入4n+2,即可得出结果;
(3)由4n+2=122,即可得出结果.
【解答】解:(1)第1个图形的顶点数为:4+2,
第2个图形的顶点数为:2×4+2,
第3个图形的顶点数为:3×4+2,
…,
第n个图形的顶点数为:n×4+2=4n+2;
(2)第12个图的顶点数为:4×12+2=50,
∴第12个图有50个顶点;
(3)4n+2=122,
解得:n=30,
∴若有122个顶点,那么它是第30个图形.
【点评】本题考查了图形的变化规律、解一元一次方程等知识;认真观察得出规律是解题的关键.
13.(2024春 海淀区期末)团扇是中国传统工艺品,代表着团圆友善、吉祥如意,某社团组织学生制作团扇,扇面有圆形和正方形两种,每种扇面面积均为300平方厘米.为了提升团扇的耐用性和美观度、需对扇面边缘用缎带进行包边处理,如图所示.
(1)圆形团扇的半径为 厘米,正方形团扇的边长为 厘米;
(2)请你通过计算说明哪种形状的扇面所用的包边长度更短.
【考点】扇形面积的计算.
【专题】与圆有关的计算;运算能力.
【答案】(1),;
(2)圆形团扇所用的包边长度更短.
【分析】(1)分别根据圆和正方形的面积公式解答即可;
(2)根据圆和正方形的周长公式解答即可.
【解答】解:(1)由题意得:
圆形团扇的半径为:(厘米),正方形团扇的边长为:(厘米),
故答案为:,;
(2)∵圆形团扇的半径为厘米,
∴圆形团扇的周长为:(厘米),
∵正方形团扇的边长为厘米,
∴正方形团扇的周长为:(厘米),
∵,3<π<4,
∴,
∴圆形团扇所用的包边长度更短.
【点评】本题考查了扇形的面积,掌握圆和正方形的面积和周长公式是解答本题的关键.
14.(2024秋 北林区校级期末)按要求计算阴影部分的面积:
(1)图1中的大圆半径等于小圆的直径,请你求出阴影部分的面积(结果保留π).
(2)如图2,已知图中长方形ABCD的面积与圆A的面积相等,且圆A的半径是3厘米,求阴影部分面积(结果保留π).
【考点】扇形面积的计算.
【专题】与圆有关的计算;运算能力.
【答案】(1)27π平方厘米;
(2)是 平方厘米.
【分析】(1)用大圆面积减去小圆面积即可;
(2)用长方形的面积减去扇形面积即可.
【解答】解:(1)π×62﹣π×()2
=36π﹣9π
=27π(平方厘米),
答:阴影部分的面积是27π平方厘米;
(2)∵长方形面积与圆面积相等,扇形的圆心角为90°,
∴S阴影部分=S矩形﹣S扇形
=S圆﹣S扇形
S圆
(平方厘米),
答:阴影部分的面积是 平方厘米.
【点评】本题考查扇形面积的计算,掌握扇形面积的计算方法是正确解答的关键.
15.(2024秋 浦东新区期末)如图,下面的爱心图案是由一个正方形和两个半圆组成,其中正方形的边长为20,请计算图中阴影部分的面积是多少?(π取3.14)
【考点】扇形面积的计算.
【专题】与圆有关的计算;运算能力.
【答案】400.
【分析】根据阴影的面积等于正方形面积减去扇形ABC的面积再加上一个圆的面积,计算即可.
【解答】解:202π×102=400﹣100π+100π=400,
答:阴影部分的面积是400.
【点评】本题考查了扇形面积的计算,关键是熟记扇形的面积公式和准确计算.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
