苏科版八年级数学上册 第一章 三角形 章节复习卷(含解析)
文档属性
| 名称 | 苏科版八年级数学上册 第一章 三角形 章节复习卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 14:00:25 | ||
图片预览



文档简介
第一章《三角形》章节复习卷
一、选择题(本大题共10小题,每小题3分,共30分)
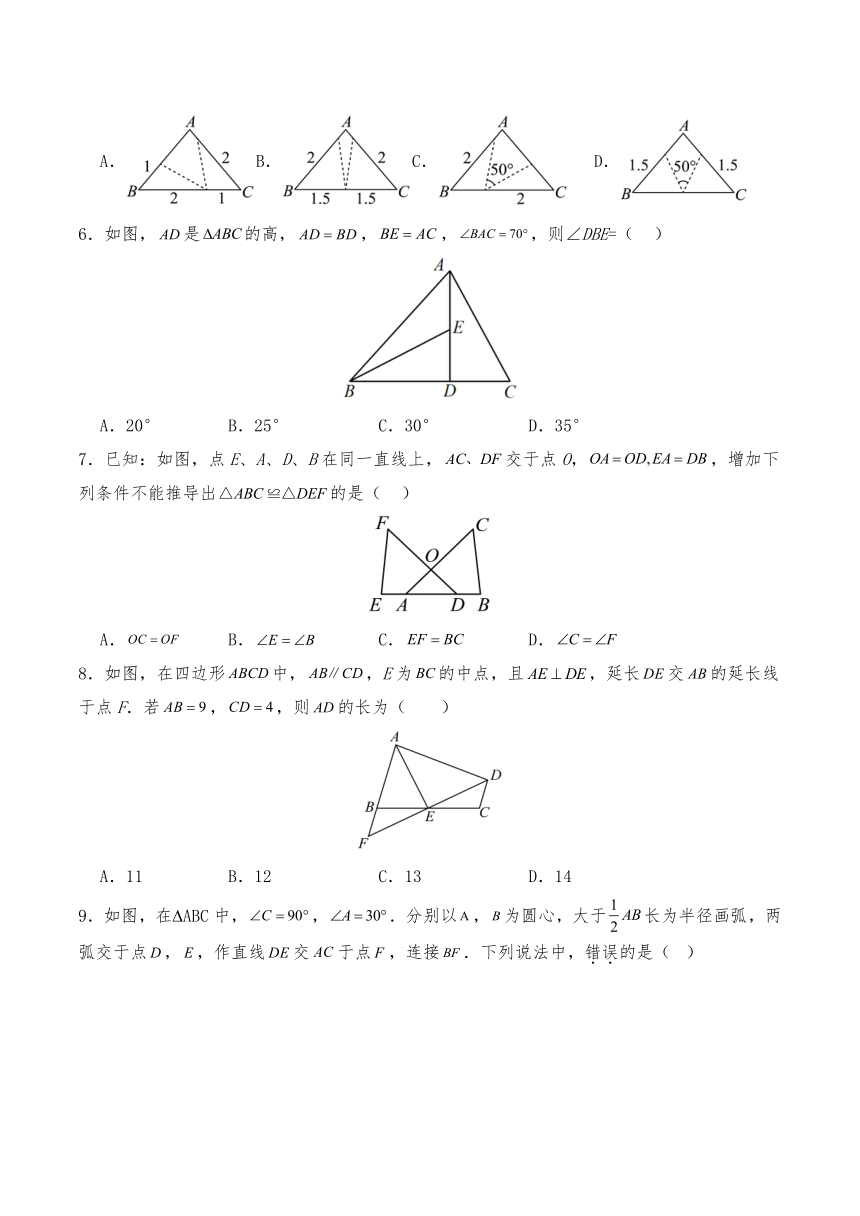
1.现有长为的铁丝,要截成小段(),每段的长度不小于,如果其中任意三小段都不能拼成三角形,则的最大值为( )
A.9 B.10 C.11 D.12
2.某校准备在如图所示的三角形空地上种植花卉,需将其分成面积相等的两块分别种植牡丹和芍药,小敏作出线段来划分,那么是 ABC的( )
A.角平分线 B.中线
C.高线 D.以上都不是
3.如图,,,则的度数为( )
A. B. C. D.
4.如图,在 ABC与中,若,则,这个结论的理由是( )
A. B. C. D.
5.在 ABC中,,将 ABC沿图中虚线剪开,剪下的两个三角形不一定全等的是( )
A.B.C. D.
6.如图,是的高,,,,则∠DBE=( )
A.20° B.25° C.30° D.35°
7.已知:如图,点E、A、D、B在同一直线上,交于点O,,增加下列条件不能推导出的是( )
A. B. C. D.
8.如图,在四边形中,,E为的中点,且,延长交的延长线于点F.若,,则的长为( )
A.11 B.12 C.13 D.14
9.如图,在 ABC中,,.分别以,为圆心,大于长为半径画弧,两弧交于点,,作直线交于点,连接.下列说法中,错误的是( )
A. B.是的平分线
C. D.
10.如图,等腰直角三角形中,,将绕点B顺时针旋转(),得到,连接,点H在射线上,则的度数( )
A.随着的增大而增大 B.随着的增大而减小
C.不变 D.随着的增大,先增大后减小
二、填空题(本大题共10小题,每小题3分,共30分)
11.若等腰三角形的周长为12,其中一边长为2,则腰长为 .
12.如图,在中,,,,P、Q是边AC、BC上的两个动点,于点D,于点E.设点P、Q运动的时间是t秒().若点P从C点出发沿CA以每秒3个单位的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回到点C停止运动;点Q从点B出发沿BC以每秒1个单位的速度向点C匀速运动,到达点C后停止运动,当 秒时,和全等.
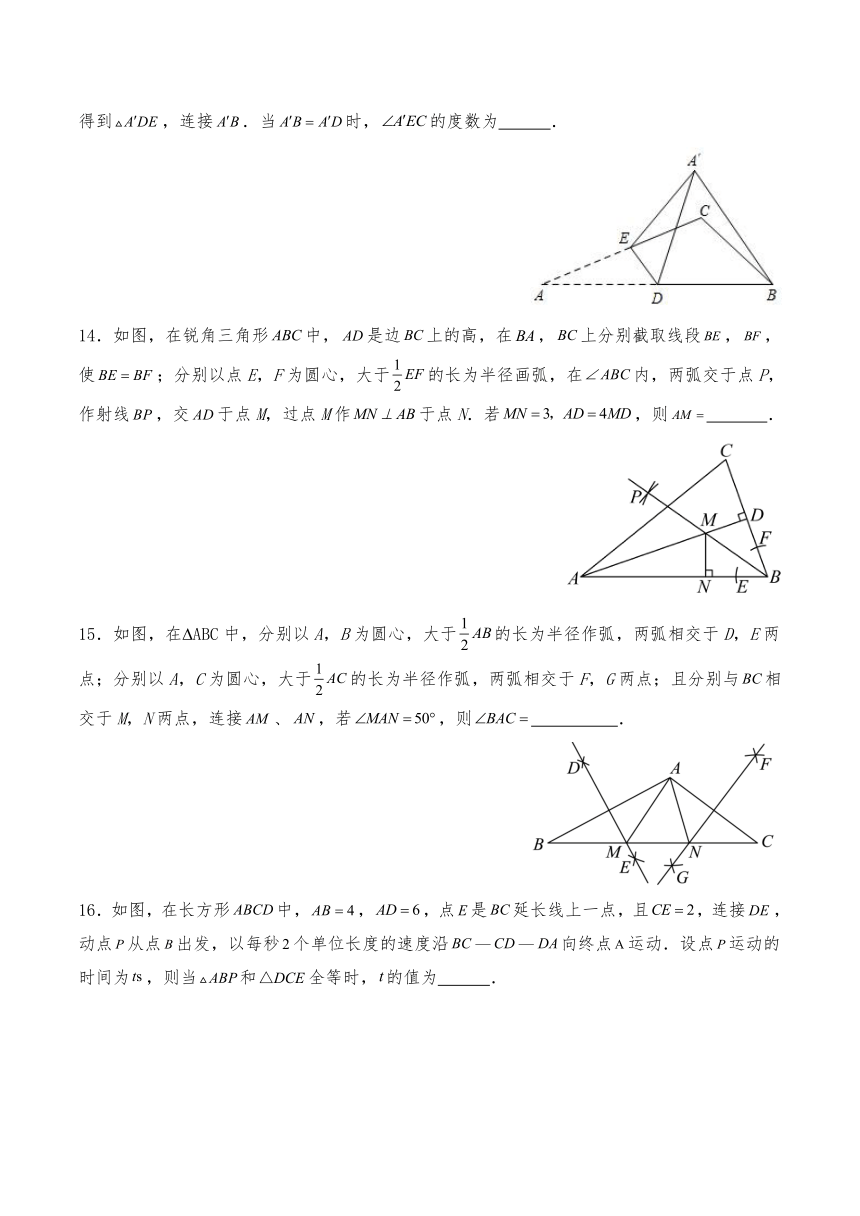
13.如图,在 ABC中,,为边中点,为边上一点,将 ADE沿着翻折,得到,连接.当时,的度数为 .
14.如图,在锐角三角形中,是边上的高,在,上分别截取线段,,使;分别以点E,F为圆心,大于的长为半径画弧,在内,两弧交于点P,作射线,交于点M,过点M作于点N.若,则 .
15.如图,在 ABC中,分别以A,B为圆心,大于的长为半径作弧,两弧相交于D,E两点;分别以A,C为圆心,大于的长为半径作弧,两弧相交于F,G两点;且分别与相交于M,N两点,连接、,若,则 .
16.如图,在长方形中,,,点是延长线上一点,且,连接,动点从点出发,以每秒个单位长度的速度沿向终点运动.设点运动的时间为,则当和全等时,的值为 .
17.如图,AD是 ABC的中线,,,,点E、F为垂足,,则BC的长为 cm.
18.如图,,点分别在射线上,,是直线上的动点,点关于对称的点为,点关于对称的点为,点在直线上运动时,当的面积最小值为时,则 OMN 的面积为 .
19.如图,在 ABC中,,,的平分线交于点,、分别是和上的动点,则的最小值是 .
20.如图,已知:,点、、…在射线上,点、、…在射线上,…均为等边三角形,若,则的边长为 .
三、解答题(本大题共5小题,共40分)
21.(6分)如图, ABC的面积为18,平分,于点D,求的面积.
22.(8分)如图①,在中,,现有一动点P,从点A出发,沿着三角形的边运动,回到点A停止,速度为,设运动时间为.
(1)如图①,当________时,的面积等于 ABC面积的一半;
(2)如图②,在中,,.在的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边运动,回到点A停止.在两点运动过程中的某一时刻,恰好,求点Q的运动速度.
23.(8分)如图,在 ABC中,点、分别在边、上,连接、交于点,且.
(1)求证:是等腰直角三角形;
(2)若,,求四边形的面积.
24.(8分)如图所示,已知四边形中,.
(1)求证:;
(2)请直接写出图中所有的全等三角形.
25.(10分)(1)如图1,在 ABC中,,,直线经过点,分别从点,向直线作垂线,垂足分别为,,求证:;
【变式探究】
(2)如图2,在 ABC中,,直线经过点,点,分别在直线上,如果,猜想,,有何数量关系,并给予证明;
【拓展应用】
(3)小明和科技兴趣小组的同学制作了一幅机器人图案,大致图形如图3所示,以 ABC的边,为一边向外作和,其中,,,是边上的高,延长交于点.设的面积为,的面积为,请猜想,大小关系,并说明理由.
参考答案
一、选择题
1.B
【知识点】三角形三边关系的应用、构成三角形的条件
【分析】本题主要考查了三角形的三边关系,即三角形的两边之和大于第三边,理解题意、列出每段铁丝的长度是解题关键.
根据三角形的三边关系,设最小的长度为,又因任意三小段都不能拼成三角形,得每段长度是,,,,,,,,,,,依此类推,总和不大于即可求解.
【详解】解:段之和为,
若要尽可能的大,则每段的长度尽可能的小,
每段的长度不小于,且其中任意三小段都不能拼成三角形,
这些小段的长度只可能分别是,,,,,,,,,,,
,
,
小段的长度分别为,,,,,,,,,,
的最大值为.
故选:B.
2.B
【知识点】根据三角形中线求面积
【分析】本题主要考查了三角形中线的性质,根据三角形的中线把三角形分为面积相等的两部分,即可解题.
【详解】解:将三角形空地分成面积相等的两部分,
是 ABC的中线;
故选:B.
3.C
【知识点】三角形内角和定理的应用、全等三角形的性质
【分析】本题考查了全等三角形的性质,三角形的内角和定理,掌握全等三角形对应角相等是解题的关键.
先根据全等三角形对应角相等得到,再由三角形内角和定理即可求解.
【详解】解:∵,
∴,
∴,
故选:C.
4.C
【知识点】用SSS证明三角形全等(SSS)
【分析】本题考查了直角三角形全等的判定的应用,注意判定两三角形的全等方法有,,,,,选用适当的方法证明两三角形全等是解题的关键.
利用证明,即可求解.
【详解】解:在 ABC与中,
∵,
∴.
故选:C
5.D
【知识点】全等三角形综合问题
【分析】本题主要考查了全等三角形的判定,三角形外角的性质,A、B两个选项都可以利用证明全等,C选项中,先证明,再利用即可证明两个三角形全等,D选项中,根据现有条件不能证明两个三角形全等.
【详解】解:A、如图所示,∵,
∴,故A不符合题意;
B、如图所示,∵,
∴,故B不符合题意;
C、如图所示,∵,,
∴,
又∵,
∴,故C不符合题意;
D、如图所示,同理可得,但是不是对应边,故不能证明两个三角形全等,故D符合题意;
故选:D.
6.B
【知识点】全等的性质和HL综合(HL)、等边对等角
【分析】证明Rt△BDE≌Rt△ADC,根据全等三角形的性质得到∠DBE=∠DAC,根据等腰直角三角形的性质求出∠DAB=∠DBA=45°,计算即可.
【详解】解:∵AD是△ABC的高,
∴∠ADB=∠ADC=90°,
在Rt△BDE和Rt△ADC中,
,
∴Rt△BDE≌Rt△ADC(HL),
∴∠DBE=∠DAC,
在Rt△ADB中,AD=BD,
∴∠DAB=∠DBA=45°,
∵∠BAC=70°,
∴∠DAC=70° 45°=25°,
∴∠DBE=∠DAC°=25°,
故选:B.
7.C
【知识点】添加条件使三角形全等(全等三角形的判定综合)
【分析】本题主要考查了全等三角形的判定,等边对等角,根据题意可证明,,再结合全等三角形的判定定理逐一判断即可.
【详解】解:∵,
∴,
∵,
∴,
∴;
添加条件,则,即,则可利用证明,故A不符合题意;
添加条件,则可利用证明,故B不符合题意;
添加条件,不可以利用证明,故C符合题意;
添加条件,则可利用证明,故D不符合题意;
故选:C.
8.C
【知识点】线段垂直平分线的性质、全等的性质和ASA(AAS)综合(ASA或者AAS)
【分析】本题考查全等三角形的判定与性质,以及垂直平分线的判定与性质,准确推导出全等三角形并理解线段垂直平分线的性质是解题关键.由“”可证,可得,,由线段垂直平分线的性质可得.
【详解】解:为的中点,
,
,
,,
在与中,
,
,
,,
,
,,
,
故选:C.
9.D
【知识点】三角形角平分线的定义、含30度角的直角三角形、线段垂直平分线的性质
【分析】本题考查了作垂直平分线,线段垂直平分线的性质,角的直角三角形的性质,先根据垂直平分线的性质判断A选项;然后利用等边对等角得到,即可判断B选项;根据角的直角三角形的性质判断C选项;然后根据高相等的两三角形的面积比等于底的比判断D选项解答即可.
【详解】解:由作图可得垂直平分,
∴,故A选项正确,不符合题意;
∴,
又∵,
∴,
∴,
∴,是的平分线,故B、C选项正确,不符合题意;
∴,故D选项错误,符合题意;
故选:D.
10.C
【知识点】根据旋转的性质求解、等腰三角形的性质和判定
【分析】本题考查了旋转的性质,等腰三角形的性质,三角形的外角性质,灵活运用这些性质解决问题是本题的关键.
由旋转的性质可得,由等腰三角形的性质和三角形内角和定理可求,由外角的性质可求,即可求解.
【详解】解:过点A作于点M,如图
∵将绕点B顺时针旋转θ(),得到,
∴,
∴,
∵,,
∴,
∵,
∴,
∴
即的度数是定值,
故选C.
二、填空题
11.5
【知识点】三角形三边关系的应用、等腰三角形的定义
【分析】要确定等腰三角形的另外两边长,可根据已知边的长,结合周长公式求解,由于长为2的边已知没有明确是腰还是底边,要分类进行讨论.
【详解】解:∵等腰三角形的周长为12,
∴当2为腰时,它的底长,,不能构成等腰三角形;
当2为底时,它的腰长,能构成等腰三角形,
即腰长为5.
故答案为:5.
12.3或6
【知识点】几何问题(一元一次方程的应用)、全等三角形的性质
【分析】分两种情况:①时,点P从C到A运动,则,求得,②时,点P从A到C运动,则,求得.
【详解】解:①时,点P从C到A运动,则,
当时,
则,
即,解得:,
②时,点P从A到C运动,则,
当时,
则,
即,
解得:,
综上所述:当秒或6秒时,.
故答案为:3或6.
13.
【知识点】三角形的外角的定义及性质、三角形折叠中的角度问题、全等三角形的性质、等边三角形的判定和性质
【分析】根据折叠的性质可得,根据及折叠的性质可得为等边三角形,再根据三角形的外角性质求解即可
【详解】在中,,将 ADE沿着翻折,交于点,得到,如图;
∴
∴,
∵,为边中点,
∴,为等边三角形,
∴,
∴,
∵
即
∴.
故答案为:
14.9
【知识点】角平分线的性质定理、作角平分线(尺规作图)
【分析】本题考查了尺规作图-作已知角的平分线,角平分线的性质,根据作图步骤可判断平分,根据角平分线的性质可得出,结合已知即可求解.
【详解】解∶由作图知∶ 平分,
∵,,,
∴,
又,
∴,
∴,
故答案为∶9.
15.
【知识点】三角形内角和定理的应用、线段垂直平分线的性质、作垂线(尺规作图)、等边对等角
【分析】本题考查了线段垂直平分线的尺规作图、等腰三角形的性质、三角形的内角和定理,熟练掌握尺规作图和等腰三角形的性质是解题关键.先得出垂直平分,垂直平分,则,再根据等腰三角形的性质可得,,然后根据三角形的内角和定理可得,根据三角形的内角和定理求解即可得.
【详解】解:由题意得:垂直平分,垂直平分,
∴,
∴,,
∵,,
∴,
∴,
∴,
故答案为:.
16.或
【知识点】全等三角形的性质
【分析】本题考查了全等三角形的性质,由题意得,,然后分当时和当时两种情况分析即可,熟练掌握全等三角形的性质是解题的关键.
【详解】解:由题意得,,
如图,当时,
∴,
∴,
∴;
如图,当时,
∴,
∴,
∴;
∴当的值为或秒时,和全等,
故答案为:或秒.
17.12
【知识点】全等的性质和ASA(AAS)综合(ASA或者AAS)、含30度角的直角三角形
【分析】先证明△CDE≌△BDF(AAS),得出DE=DF=EF=3cm,再由,,求得,从而求出∠DCE=30°,由直角三角形的性质得出CD=2DE=6cm,即可由BC=2CD求解.
【详解】解:∵AD是 ABC的中线,
∴.
∵,,
∴,
在和 BDF中,
,
∴(AAS).
∴.
∵,,
∴,
∴
∴,
∴.
故答案为:12.
18.
【知识点】等腰三角形的性质和判定、根据成轴对称图形的特征进行求解
【分析】连接,过点作于,根据轴对称的性质可得,,,即得,得到为等腰直角三角形,即得,可知当的面积最小时,点在点位置,即,可得,最后根据三角形面积公式计算即可求解.
【详解】解:如图,连接,过点作于,
由轴对称可得,,,,,
∴,,,
∴,
∴为等腰直角三角形,
∴,
当的面积最小时,点在点位置,即,
解得,
∴,
故答案为:.
19.
【知识点】垂线段最短、含30度角的直角三角形、角平分线的性质定理
【分析】本题考查了角平分线的性质,含角的直角三角形,垂线段最短,解题的关键是正确作出辅助线.
作于点,根据垂线段最短可知,的最小值是线段的长度,根据解含角的直角三角形即可.
【详解】解:如图,作于点,
∵平分,
作点关于的对称点,
∴,
∵,,
∴,
∴,
∴的最小值是,
故答案为:.
20.
【知识点】等边三角形的性质、含30度角的直角三角形、两直线平行同位角相等
【分析】考查了等边三角形的性质以及等腰三角形的性质,根据已知得出进而发现规律是解题关键.
根据等腰三角形的性质以及平行线的性质得出,以及,得出…进而得出答案.
【详解】解:如图所示:
∵是等边三角形,
∴,
∴,
,
∴,
又∵,
,
∵,
,
∴,
∵是等边三角形,
∴,
,
∴,
∴,
∴,
∴,,,
以此类推:.
故答案是:.
三、解答题
21.解:如图,延长交于点,
平分,,
∴∠BAD=∠EAD,,
在和中,
,
,
,
,,
,
.
22.(1)解:∵在中,,
∴,
∴.
分类讨论:①当点P在上时,不存在;
②当点P在上时,此时,如图,
∴,
∴;
③当点P在上时,此时,如图,
∵的面积等于 ABC面积的一半,
∴,
∴,
∴.
综上可知当或时,的面积等于 ABC面积的一半;
(2)解:∵,
∴只存在两种情况:①当点P位于,点Q位于上时;②当点Q位于,点P位于上时.
设点Q的运动速度为,
①当点P位于,点Q位于上时,此时,,如图,
∵,
∴,,
∴,,
解得:,,
∴此时点Q的运动速度为;
②当点Q位于,点P位于上时,此时,,如图,
∵,
∴,,
∴,,
解得:,,
∴此时点Q的运动速度为.
综上可知点Q的运动速度为或.
23.(1)证明:,
,,
,
,
是等腰直角三角形;
(2)解:,,
,
,
,
四边形的面积.
24.(1)证明:∵,
∴,
∵,
∴,
∴,
在和 ADE中
,
∴,
∴.
(2)解:在 ABC和中,
,
∴,
∴,,
在和中,
,
∴.
由(1)有,
综上,图中全等三角形有:、、.
25.(1)证明:∵直线l,直线l,
∴,
∴,
∵,
∴,
∴,
在和中,
,
∴;
(2)解:,,的数量关系是:,证明如下:
∵是的外角,
∴∠EAB=∠ADB+∠DBA,
∴∠EAC+∠BAC=∠ADB+∠DBA,
∵,
∴,
在和中,
,
∴,
∴,,
∴;
(3),大小关系是:,理由如下:
过点D作交的延长线于点M,过点E作于点N,如图所示:
∵,
∴∠AGB=∠M=90°,
∴,
∵,
∴∠BAG+∠DAM=90°,
∴∠ABG=∠DAM,
在和中,
,
∴,
∴,
同理可证明:,
∴,
∴,
∵,,
∴.
一、选择题(本大题共10小题,每小题3分,共30分)
1.现有长为的铁丝,要截成小段(),每段的长度不小于,如果其中任意三小段都不能拼成三角形,则的最大值为( )
A.9 B.10 C.11 D.12
2.某校准备在如图所示的三角形空地上种植花卉,需将其分成面积相等的两块分别种植牡丹和芍药,小敏作出线段来划分,那么是 ABC的( )
A.角平分线 B.中线
C.高线 D.以上都不是
3.如图,,,则的度数为( )
A. B. C. D.
4.如图,在 ABC与中,若,则,这个结论的理由是( )
A. B. C. D.
5.在 ABC中,,将 ABC沿图中虚线剪开,剪下的两个三角形不一定全等的是( )
A.B.C. D.
6.如图,是的高,,,,则∠DBE=( )
A.20° B.25° C.30° D.35°
7.已知:如图,点E、A、D、B在同一直线上,交于点O,,增加下列条件不能推导出的是( )
A. B. C. D.
8.如图,在四边形中,,E为的中点,且,延长交的延长线于点F.若,,则的长为( )
A.11 B.12 C.13 D.14
9.如图,在 ABC中,,.分别以,为圆心,大于长为半径画弧,两弧交于点,,作直线交于点,连接.下列说法中,错误的是( )
A. B.是的平分线
C. D.
10.如图,等腰直角三角形中,,将绕点B顺时针旋转(),得到,连接,点H在射线上,则的度数( )
A.随着的增大而增大 B.随着的增大而减小
C.不变 D.随着的增大,先增大后减小
二、填空题(本大题共10小题,每小题3分,共30分)
11.若等腰三角形的周长为12,其中一边长为2,则腰长为 .
12.如图,在中,,,,P、Q是边AC、BC上的两个动点,于点D,于点E.设点P、Q运动的时间是t秒().若点P从C点出发沿CA以每秒3个单位的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回到点C停止运动;点Q从点B出发沿BC以每秒1个单位的速度向点C匀速运动,到达点C后停止运动,当 秒时,和全等.
13.如图,在 ABC中,,为边中点,为边上一点,将 ADE沿着翻折,得到,连接.当时,的度数为 .
14.如图,在锐角三角形中,是边上的高,在,上分别截取线段,,使;分别以点E,F为圆心,大于的长为半径画弧,在内,两弧交于点P,作射线,交于点M,过点M作于点N.若,则 .
15.如图,在 ABC中,分别以A,B为圆心,大于的长为半径作弧,两弧相交于D,E两点;分别以A,C为圆心,大于的长为半径作弧,两弧相交于F,G两点;且分别与相交于M,N两点,连接、,若,则 .
16.如图,在长方形中,,,点是延长线上一点,且,连接,动点从点出发,以每秒个单位长度的速度沿向终点运动.设点运动的时间为,则当和全等时,的值为 .
17.如图,AD是 ABC的中线,,,,点E、F为垂足,,则BC的长为 cm.
18.如图,,点分别在射线上,,是直线上的动点,点关于对称的点为,点关于对称的点为,点在直线上运动时,当的面积最小值为时,则 OMN 的面积为 .
19.如图,在 ABC中,,,的平分线交于点,、分别是和上的动点,则的最小值是 .
20.如图,已知:,点、、…在射线上,点、、…在射线上,…均为等边三角形,若,则的边长为 .
三、解答题(本大题共5小题,共40分)
21.(6分)如图, ABC的面积为18,平分,于点D,求的面积.
22.(8分)如图①,在中,,现有一动点P,从点A出发,沿着三角形的边运动,回到点A停止,速度为,设运动时间为.
(1)如图①,当________时,的面积等于 ABC面积的一半;
(2)如图②,在中,,.在的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边运动,回到点A停止.在两点运动过程中的某一时刻,恰好,求点Q的运动速度.
23.(8分)如图,在 ABC中,点、分别在边、上,连接、交于点,且.
(1)求证:是等腰直角三角形;
(2)若,,求四边形的面积.
24.(8分)如图所示,已知四边形中,.
(1)求证:;
(2)请直接写出图中所有的全等三角形.
25.(10分)(1)如图1,在 ABC中,,,直线经过点,分别从点,向直线作垂线,垂足分别为,,求证:;
【变式探究】
(2)如图2,在 ABC中,,直线经过点,点,分别在直线上,如果,猜想,,有何数量关系,并给予证明;
【拓展应用】
(3)小明和科技兴趣小组的同学制作了一幅机器人图案,大致图形如图3所示,以 ABC的边,为一边向外作和,其中,,,是边上的高,延长交于点.设的面积为,的面积为,请猜想,大小关系,并说明理由.
参考答案
一、选择题
1.B
【知识点】三角形三边关系的应用、构成三角形的条件
【分析】本题主要考查了三角形的三边关系,即三角形的两边之和大于第三边,理解题意、列出每段铁丝的长度是解题关键.
根据三角形的三边关系,设最小的长度为,又因任意三小段都不能拼成三角形,得每段长度是,,,,,,,,,,,依此类推,总和不大于即可求解.
【详解】解:段之和为,
若要尽可能的大,则每段的长度尽可能的小,
每段的长度不小于,且其中任意三小段都不能拼成三角形,
这些小段的长度只可能分别是,,,,,,,,,,,
,
,
小段的长度分别为,,,,,,,,,,
的最大值为.
故选:B.
2.B
【知识点】根据三角形中线求面积
【分析】本题主要考查了三角形中线的性质,根据三角形的中线把三角形分为面积相等的两部分,即可解题.
【详解】解:将三角形空地分成面积相等的两部分,
是 ABC的中线;
故选:B.
3.C
【知识点】三角形内角和定理的应用、全等三角形的性质
【分析】本题考查了全等三角形的性质,三角形的内角和定理,掌握全等三角形对应角相等是解题的关键.
先根据全等三角形对应角相等得到,再由三角形内角和定理即可求解.
【详解】解:∵,
∴,
∴,
故选:C.
4.C
【知识点】用SSS证明三角形全等(SSS)
【分析】本题考查了直角三角形全等的判定的应用,注意判定两三角形的全等方法有,,,,,选用适当的方法证明两三角形全等是解题的关键.
利用证明,即可求解.
【详解】解:在 ABC与中,
∵,
∴.
故选:C
5.D
【知识点】全等三角形综合问题
【分析】本题主要考查了全等三角形的判定,三角形外角的性质,A、B两个选项都可以利用证明全等,C选项中,先证明,再利用即可证明两个三角形全等,D选项中,根据现有条件不能证明两个三角形全等.
【详解】解:A、如图所示,∵,
∴,故A不符合题意;
B、如图所示,∵,
∴,故B不符合题意;
C、如图所示,∵,,
∴,
又∵,
∴,故C不符合题意;
D、如图所示,同理可得,但是不是对应边,故不能证明两个三角形全等,故D符合题意;
故选:D.
6.B
【知识点】全等的性质和HL综合(HL)、等边对等角
【分析】证明Rt△BDE≌Rt△ADC,根据全等三角形的性质得到∠DBE=∠DAC,根据等腰直角三角形的性质求出∠DAB=∠DBA=45°,计算即可.
【详解】解:∵AD是△ABC的高,
∴∠ADB=∠ADC=90°,
在Rt△BDE和Rt△ADC中,
,
∴Rt△BDE≌Rt△ADC(HL),
∴∠DBE=∠DAC,
在Rt△ADB中,AD=BD,
∴∠DAB=∠DBA=45°,
∵∠BAC=70°,
∴∠DAC=70° 45°=25°,
∴∠DBE=∠DAC°=25°,
故选:B.
7.C
【知识点】添加条件使三角形全等(全等三角形的判定综合)
【分析】本题主要考查了全等三角形的判定,等边对等角,根据题意可证明,,再结合全等三角形的判定定理逐一判断即可.
【详解】解:∵,
∴,
∵,
∴,
∴;
添加条件,则,即,则可利用证明,故A不符合题意;
添加条件,则可利用证明,故B不符合题意;
添加条件,不可以利用证明,故C符合题意;
添加条件,则可利用证明,故D不符合题意;
故选:C.
8.C
【知识点】线段垂直平分线的性质、全等的性质和ASA(AAS)综合(ASA或者AAS)
【分析】本题考查全等三角形的判定与性质,以及垂直平分线的判定与性质,准确推导出全等三角形并理解线段垂直平分线的性质是解题关键.由“”可证,可得,,由线段垂直平分线的性质可得.
【详解】解:为的中点,
,
,
,,
在与中,
,
,
,,
,
,,
,
故选:C.
9.D
【知识点】三角形角平分线的定义、含30度角的直角三角形、线段垂直平分线的性质
【分析】本题考查了作垂直平分线,线段垂直平分线的性质,角的直角三角形的性质,先根据垂直平分线的性质判断A选项;然后利用等边对等角得到,即可判断B选项;根据角的直角三角形的性质判断C选项;然后根据高相等的两三角形的面积比等于底的比判断D选项解答即可.
【详解】解:由作图可得垂直平分,
∴,故A选项正确,不符合题意;
∴,
又∵,
∴,
∴,
∴,是的平分线,故B、C选项正确,不符合题意;
∴,故D选项错误,符合题意;
故选:D.
10.C
【知识点】根据旋转的性质求解、等腰三角形的性质和判定
【分析】本题考查了旋转的性质,等腰三角形的性质,三角形的外角性质,灵活运用这些性质解决问题是本题的关键.
由旋转的性质可得,由等腰三角形的性质和三角形内角和定理可求,由外角的性质可求,即可求解.
【详解】解:过点A作于点M,如图
∵将绕点B顺时针旋转θ(),得到,
∴,
∴,
∵,,
∴,
∵,
∴,
∴
即的度数是定值,
故选C.
二、填空题
11.5
【知识点】三角形三边关系的应用、等腰三角形的定义
【分析】要确定等腰三角形的另外两边长,可根据已知边的长,结合周长公式求解,由于长为2的边已知没有明确是腰还是底边,要分类进行讨论.
【详解】解:∵等腰三角形的周长为12,
∴当2为腰时,它的底长,,不能构成等腰三角形;
当2为底时,它的腰长,能构成等腰三角形,
即腰长为5.
故答案为:5.
12.3或6
【知识点】几何问题(一元一次方程的应用)、全等三角形的性质
【分析】分两种情况:①时,点P从C到A运动,则,求得,②时,点P从A到C运动,则,求得.
【详解】解:①时,点P从C到A运动,则,
当时,
则,
即,解得:,
②时,点P从A到C运动,则,
当时,
则,
即,
解得:,
综上所述:当秒或6秒时,.
故答案为:3或6.
13.
【知识点】三角形的外角的定义及性质、三角形折叠中的角度问题、全等三角形的性质、等边三角形的判定和性质
【分析】根据折叠的性质可得,根据及折叠的性质可得为等边三角形,再根据三角形的外角性质求解即可
【详解】在中,,将 ADE沿着翻折,交于点,得到,如图;
∴
∴,
∵,为边中点,
∴,为等边三角形,
∴,
∴,
∵
即
∴.
故答案为:
14.9
【知识点】角平分线的性质定理、作角平分线(尺规作图)
【分析】本题考查了尺规作图-作已知角的平分线,角平分线的性质,根据作图步骤可判断平分,根据角平分线的性质可得出,结合已知即可求解.
【详解】解∶由作图知∶ 平分,
∵,,,
∴,
又,
∴,
∴,
故答案为∶9.
15.
【知识点】三角形内角和定理的应用、线段垂直平分线的性质、作垂线(尺规作图)、等边对等角
【分析】本题考查了线段垂直平分线的尺规作图、等腰三角形的性质、三角形的内角和定理,熟练掌握尺规作图和等腰三角形的性质是解题关键.先得出垂直平分,垂直平分,则,再根据等腰三角形的性质可得,,然后根据三角形的内角和定理可得,根据三角形的内角和定理求解即可得.
【详解】解:由题意得:垂直平分,垂直平分,
∴,
∴,,
∵,,
∴,
∴,
∴,
故答案为:.
16.或
【知识点】全等三角形的性质
【分析】本题考查了全等三角形的性质,由题意得,,然后分当时和当时两种情况分析即可,熟练掌握全等三角形的性质是解题的关键.
【详解】解:由题意得,,
如图,当时,
∴,
∴,
∴;
如图,当时,
∴,
∴,
∴;
∴当的值为或秒时,和全等,
故答案为:或秒.
17.12
【知识点】全等的性质和ASA(AAS)综合(ASA或者AAS)、含30度角的直角三角形
【分析】先证明△CDE≌△BDF(AAS),得出DE=DF=EF=3cm,再由,,求得,从而求出∠DCE=30°,由直角三角形的性质得出CD=2DE=6cm,即可由BC=2CD求解.
【详解】解:∵AD是 ABC的中线,
∴.
∵,,
∴,
在和 BDF中,
,
∴(AAS).
∴.
∵,,
∴,
∴
∴,
∴.
故答案为:12.
18.
【知识点】等腰三角形的性质和判定、根据成轴对称图形的特征进行求解
【分析】连接,过点作于,根据轴对称的性质可得,,,即得,得到为等腰直角三角形,即得,可知当的面积最小时,点在点位置,即,可得,最后根据三角形面积公式计算即可求解.
【详解】解:如图,连接,过点作于,
由轴对称可得,,,,,
∴,,,
∴,
∴为等腰直角三角形,
∴,
当的面积最小时,点在点位置,即,
解得,
∴,
故答案为:.
19.
【知识点】垂线段最短、含30度角的直角三角形、角平分线的性质定理
【分析】本题考查了角平分线的性质,含角的直角三角形,垂线段最短,解题的关键是正确作出辅助线.
作于点,根据垂线段最短可知,的最小值是线段的长度,根据解含角的直角三角形即可.
【详解】解:如图,作于点,
∵平分,
作点关于的对称点,
∴,
∵,,
∴,
∴,
∴的最小值是,
故答案为:.
20.
【知识点】等边三角形的性质、含30度角的直角三角形、两直线平行同位角相等
【分析】考查了等边三角形的性质以及等腰三角形的性质,根据已知得出进而发现规律是解题关键.
根据等腰三角形的性质以及平行线的性质得出,以及,得出…进而得出答案.
【详解】解:如图所示:
∵是等边三角形,
∴,
∴,
,
∴,
又∵,
,
∵,
,
∴,
∵是等边三角形,
∴,
,
∴,
∴,
∴,
∴,,,
以此类推:.
故答案是:.
三、解答题
21.解:如图,延长交于点,
平分,,
∴∠BAD=∠EAD,,
在和中,
,
,
,
,,
,
.
22.(1)解:∵在中,,
∴,
∴.
分类讨论:①当点P在上时,不存在;
②当点P在上时,此时,如图,
∴,
∴;
③当点P在上时,此时,如图,
∵的面积等于 ABC面积的一半,
∴,
∴,
∴.
综上可知当或时,的面积等于 ABC面积的一半;
(2)解:∵,
∴只存在两种情况:①当点P位于,点Q位于上时;②当点Q位于,点P位于上时.
设点Q的运动速度为,
①当点P位于,点Q位于上时,此时,,如图,
∵,
∴,,
∴,,
解得:,,
∴此时点Q的运动速度为;
②当点Q位于,点P位于上时,此时,,如图,
∵,
∴,,
∴,,
解得:,,
∴此时点Q的运动速度为.
综上可知点Q的运动速度为或.
23.(1)证明:,
,,
,
,
是等腰直角三角形;
(2)解:,,
,
,
,
四边形的面积.
24.(1)证明:∵,
∴,
∵,
∴,
∴,
在和 ADE中
,
∴,
∴.
(2)解:在 ABC和中,
,
∴,
∴,,
在和中,
,
∴.
由(1)有,
综上,图中全等三角形有:、、.
25.(1)证明:∵直线l,直线l,
∴,
∴,
∵,
∴,
∴,
在和中,
,
∴;
(2)解:,,的数量关系是:,证明如下:
∵是的外角,
∴∠EAB=∠ADB+∠DBA,
∴∠EAC+∠BAC=∠ADB+∠DBA,
∵,
∴,
在和中,
,
∴,
∴,,
∴;
(3),大小关系是:,理由如下:
过点D作交的延长线于点M,过点E作于点N,如图所示:
∵,
∴∠AGB=∠M=90°,
∴,
∵,
∴∠BAG+∠DAM=90°,
∴∠ABG=∠DAM,
在和中,
,
∴,
∴,
同理可证明:,
∴,
∴,
∵,,
∴.
同课章节目录
