4.4一次函数的应用(预习衔接.夯实基础.含解析)-2025-2026学年八年级上册数学北师大版(2024)
文档属性
| 名称 | 4.4一次函数的应用(预习衔接.夯实基础.含解析)-2025-2026学年八年级上册数学北师大版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 976.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 20:51:43 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
预习衔接.夯实基础 一次函数的应用
一.选择题(共5小题)
1.(2024秋 雁塔区校级期中)在一定范围内,弹簧的受力和伸长长度成正比.某次数学实验中,同学们记录了同一根弹簧的长度y(cm)和所挂物体质量x(kg)(0≤x≤12)的对应数据如表(部分)所示,下列说法中不正确的是( )
x(kg) 1 2 3 4 …
y(cm) 10.5 11 11.5 12 …
A.x,y都是变量,y是x的一次函数
B.弹簧不挂物体时的长度是10cm
C.当所挂物体的质量为10kg时,弹簧长度是15cm
D.物体质量由4kg增加到7kg,弹簧的长度增加1cm
2.(2024秋 深圳期中)甲、乙两人同起点同方向出发,匀速步行3000米,先到终点的人原地休息.已知甲先出发3分钟,甲、乙两人之间的距离y(米)与甲出发的时间t(分)之间的关系如图所示,则下列说法正确是( )
A.甲步行的平均速度为32米/分
B.乙步行的平均速度为20米/分
C.当t=30时,乙到达终点
D.乙比甲提前4.5分钟到达终点
3.(2024 青山区模拟)漏刻是我国古代的一种计时工具,据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用,小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现水位h(cm)是时间t(min)的一次函数,如下表是小明记录的部分数据,当时间t为10时,对应的高度h为( )
t(min) … 0 1 2 3 …
h(cm) … 0.7 1.1 1.5 1.9 …
A.3.3 B.3.65 C.3.9 D.4.7
4.(2024秋 荥阳市期中)甲、乙两车从A地出发,沿同一路线驶向B地,甲车先出发匀速驶向B地,40min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了50km/h,结果与甲车同时到达B地.甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:
①a=4.5;
②甲的速度是60km/h;
③乙刚开始的速度是80km/h;
④乙出发第一次追上甲用时80min.
其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
5.(2024秋 市中区期中)如图1是某湖最深处的一个截面图,湖水面下任意一点A的压强P(单位:cmHg)与其离水面的深度h(单位:m)的函数解析式为P=ah+P0,其图象如图2所示,其中P0为湖水面大气压强,a为常数且a>0,点M的坐标为(34.5,342),根据图中信息分析,下列结论正确的是( )
A.湖水面大气压强为76.0cmHg
B.函数解析式P=ah+P0中P的取值范围是P<342
C.湖水深20m处的压强为256cmHg
D.P与h的函数解析式为P=8h+66(0≤h≤34.5)
二.填空题(共5小题)
6.(2024秋 市南区校级期中)某公司生产了A,B两款新能源电动汽车.如图,l1,l2分别表示A款,B款新能源电动汽车充满电后电池的剩余电量y(kw h)与汽车行驶路程x(km)的关系.当两款新能源电动汽车的行驶路程都是250km时,A款新能源电动汽车电池的剩余电量比B款新能源电动汽车电池的剩余电量多 kw h.
7.(2024秋 历下区期中)A,B两地相距30km,甲、乙两人沿同一条路从A地到B地.甲骑自行车以10km/h的速度先出发,1.5小时后,乙开车以40km/h的速度出发.两人之间的距离s(km)与甲出发的时间t(h)的函数关系如图所示,当乙到达B地时两人相距 km.
8.(2024春 三门县期末)一个弹簧不挂重物时长12cm,挂上重物后伸长的长度与所挂重物的质量成正比.如果挂上1kg的物体后,弹簧伸长2cm,弹簧的总长度y cm与所挂物体的质量x kg的函数表达式是 .
9.(2024秋 龙华区期中)同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数关系是yx+32,如果某一温度的摄氏度数是5℃,那么它的华氏度数是 ℉.
10.(2024秋 潍坊期中)火星探测车是登陆火星并进行探测的可移动探测器,为应对极端温度环境,制造火星车使用的是新型隔温材料——纳米气凝胶,该材料导热率(W/m K)与温度(℃)的关系如表:
温度(℃) 100 150 200 250 300
导热率(W/m K) 0.15 0.2 0.25 0.3 0.35
根据表格中两者的对应关系,若导热率为0.75W/m K,则温度为 ℃.
三.解答题(共5小题)
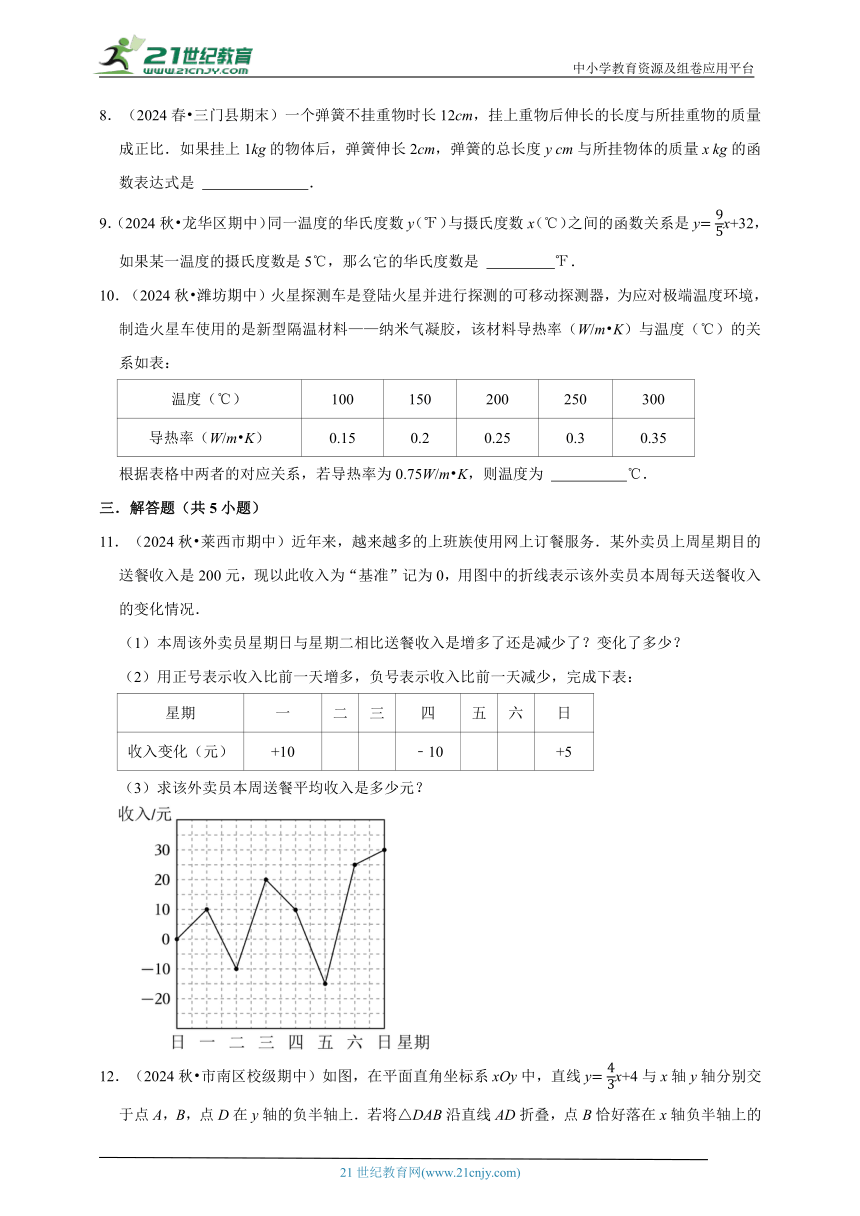
11.(2024秋 莱西市期中)近年来,越来越多的上班族使用网上订餐服务.某外卖员上周星期目的送餐收入是200元,现以此收入为“基准”记为0,用图中的折线表示该外卖员本周每天送餐收入的变化情况.
(1)本周该外卖员星期日与星期二相比送餐收入是增多了还是减少了?变化了多少?
(2)用正号表示收入比前一天增多,负号表示收入比前一天减少,完成下表:
星期 一 二 三 四 五 六 日
收入变化(元) +10 ﹣10 +5
(3)求该外卖员本周送餐平均收入是多少元?
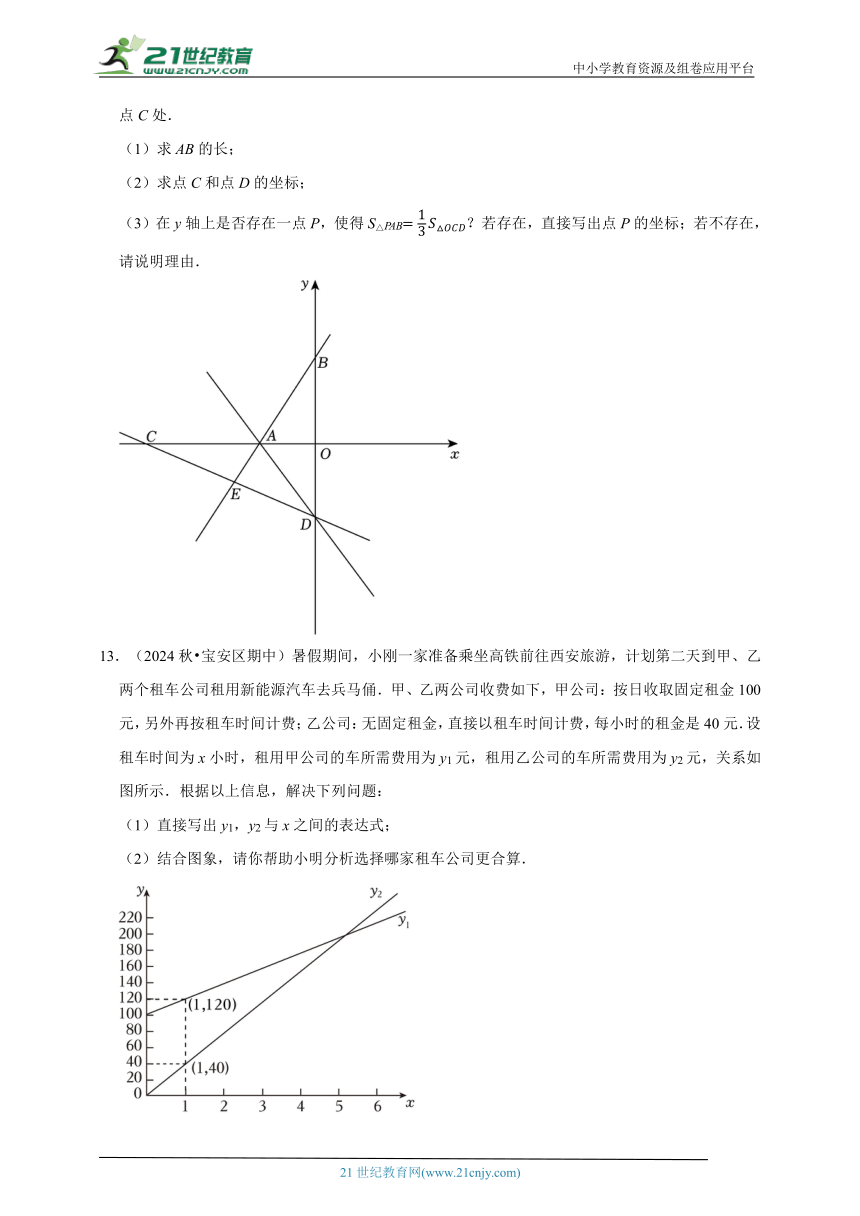
12.(2024秋 市南区校级期中)如图,在平面直角坐标系xOy中,直线yx+4与x轴y轴分别交于点A,B,点D在y轴的负半轴上.若将△DAB沿直线AD折叠,点B恰好落在x轴负半轴上的点C处.
(1)求AB的长;
(2)求点C和点D的坐标;
(3)在y轴上是否存在一点P,使得S△PAB?若存在,直接写出点P的坐标;若不存在,请说明理由.
13.(2024秋 宝安区期中)暑假期间,小刚一家准备乘坐高铁前往西安旅游,计划第二天到甲、乙两个租车公司租用新能源汽车去兵马俑.甲、乙两公司收费如下,甲公司:按日收取固定租金100元,另外再按租车时间计费;乙公司:无固定租金,直接以租车时间计费,每小时的租金是40元.设租车时间为x小时,租用甲公司的车所需费用为y1元,租用乙公司的车所需费用为y2元,关系如图所示.根据以上信息,解决下列问题:
(1)直接写出y1,y2与x之间的表达式;
(2)结合图象,请你帮助小明分析选择哪家租车公司更合算.
14.(2024秋 市南区校级期中)“漏壶”是一种古代计时器,在社会实践活动中,某小组同学根据“漏壶”的原理制作了如图①所示的液体漏壶,漏壶是由一个圆锥和一个圆柱组成的,中间连通,液体可以从圆锥容器中匀速漏到圆柱容器中,实验开始时圆柱容器中已有一部分液体.
(1)表是实验记录的圆柱体容器液面高度y(厘米)与时间x(小时)的数据:
时间x(小时) 0 1 2 3 4
圆柱体容器液面高度y(厘米) 2 6 10 14 18
在如图②所示的直角坐标系中描出如表的各点,用光滑的线连接;
(2)请根据(1)中的数据确定y与x之间的函数表达式;
(3)如果本次实验记录的开始时间是上午8:00,那么当圆柱体容器液面高度达到16厘米时是几点?
15.(2024秋 罗湖区校级期中)我校将举办一年一度的秋季运动会,需要采购一批某品牌的乒乓球拍和配套的乒乓球,一副球拍标价80元,一盒球标价25元.体育商店提供了两种优惠方案,具体如下:
方案甲:买一副乒乓球拍送一盒乒乓球,其余乒乓球按原价出售;
方案乙:按购买金额打9折付款.
学校欲购买这种乒乓球拍10副,乒乓球x(x 10)盒.
(1)请直接写出两种优惠办法实际付款金额y甲(元),y乙(元)与x(盒)之间的函数关系式.
(2)如果学校提供经费为1800元,选择哪个方案能购买更多乒乓球?
预习衔接.夯实基础 一次函数的应用
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 雁塔区校级期中)在一定范围内,弹簧的受力和伸长长度成正比.某次数学实验中,同学们记录了同一根弹簧的长度y(cm)和所挂物体质量x(kg)(0≤x≤12)的对应数据如表(部分)所示,下列说法中不正确的是( )
x(kg) 1 2 3 4 …
y(cm) 10.5 11 11.5 12 …
A.x,y都是变量,y是x的一次函数
B.弹簧不挂物体时的长度是10cm
C.当所挂物体的质量为10kg时,弹簧长度是15cm
D.物体质量由4kg增加到7kg,弹簧的长度增加1cm
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】D
【分析】A.根据变量的定义及“所挂物体的质量x增加1kg,弹簧的长度y伸长0.5cm”判断即可;
B.利用待定系数法求出y与x之间的函数关系式,将x=0代入该函数求出对应y的值即可;
C.将x=10代入该函数求出对应y的值即可;
D.分别将x=4和x=7代入y与x之间的函数关系式,求出对应的y值并求差即可.
【解答】解:∵x,y都是变量,且所挂物体的质量x增加1kg,弹簧的长度y伸长0.5cm,
∴弹簧的长度y和所挂物体质量x的一次函数,
∴A正确,不符合题意;
设y与x之间的函数关系式为y=kx+b(k、b为常数,且k≠0),
把x=2,y=11和x=4,y=12分别代入y=kx+b,
得,
解得,
∴y与x之间的函数关系式为y=0.5x+10,
当x=0时,y=10,
∴弹簧不挂物体时的长度是10cm,
∴B正确,不符合题意;
当x=10时,y=0.5×10+10=15,
∴当所挂物体的质量为10kg时,弹簧长度是15cm,
∴C正确,不符合题意;
当x=4时,y=0.5×4+10=12,
当x=7时,y=0.5×7+10=13.5,
13.5﹣12=1.5(cm),
∴物体质量由4kg增加到7kg,弹簧的长度增加1.5cm,
∴D不正确,符合题意.
故选:D.
【点评】本题考查一次函数的应用,掌握变量的定义、一次函数的判断方法是解题的关键.
2.(2024秋 深圳期中)甲、乙两人同起点同方向出发,匀速步行3000米,先到终点的人原地休息.已知甲先出发3分钟,甲、乙两人之间的距离y(米)与甲出发的时间t(分)之间的关系如图所示,则下列说法正确是( )
A.甲步行的平均速度为32米/分
B.乙步行的平均速度为20米/分
C.当t=30时,乙到达终点
D.乙比甲提前4.5分钟到达终点
【考点】一次函数的应用.
【专题】一次函数及其应用;应用意识.
【答案】D
【分析】根据函数图象,求出甲、乙的速度,再求出它们到达终点的时间即可求解.
【解答】解:由图可得,甲的速度为240÷3=80(米/分),故选项A不符合题意;
设乙的速度为x米/分,
由图可得,(15﹣3)x=240+80×(15﹣3),
解得x=100,
∴乙的速度为100米/分,故选项B不符合题意;
∴甲到达终点的时间为3000÷80=37.5(分钟),
乙达到终点的时间为3000÷100=30(分钟),
30+3=33(分钟),
即当t=33时,乙到达终点,故选项C不符合题意;
∵甲先出发3分钟,
∴乙先到终点原地休息了37.5﹣3﹣30=4.5(分钟),
即乙比甲提前4.5分钟到达终点.
故说法正确是D.
故选:D.
【点评】本题考查了一次函数的应用,看懂函数的图象是解题的关键.
3.(2024 青山区模拟)漏刻是我国古代的一种计时工具,据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用,小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现水位h(cm)是时间t(min)的一次函数,如下表是小明记录的部分数据,当时间t为10时,对应的高度h为( )
t(min) … 0 1 2 3 …
h(cm) … 0.7 1.1 1.5 1.9 …
A.3.3 B.3.65 C.3.9 D.4.7
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力.
【答案】D
【分析】设水位h(cm)与时间t(min)的关系式h=kt+b,用待定系数法求出解析式即可.
【解答】解:设水位h(cm)与时间t(min)的关系式h=kt+b,
把t=0,h=0.7和t=1,h=1.1代入表中数据得:,
解得:,
∴水位h(cm)与时间t(min)的关系式h=0.4t+0.7.
把t=10代入h=0.4t+0.7中,得h=0.4×10+0.7=4.7,
故选:D.
【点评】本题考查一次函数的知识,熟练掌握待定系数法求解析式是解题的关键.
4.(2024秋 荥阳市期中)甲、乙两车从A地出发,沿同一路线驶向B地,甲车先出发匀速驶向B地,40min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了50km/h,结果与甲车同时到达B地.甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:
①a=4.5;
②甲的速度是60km/h;
③乙刚开始的速度是80km/h;
④乙出发第一次追上甲用时80min.
其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
【考点】一次函数的应用.
【专题】一次函数及其应用;几何直观;运算能力;应用意识.
【答案】B
【分析】根据题意和函数图象中的数据,可以计算出各个小题中的结论是否正确,从而可以解答本题.
【解答】解:由图象可得,
a=4+0.5=4.5,故①正确;
甲的速度是460÷(7)=60(km/h),故②正确;
设乙刚开始的速度是v km/h,则后来的速度为(v﹣50)km/h,
4v+(7﹣4.5)×(v﹣50)=460,
解得v=90,故③错误;
设乙出发第一次追上甲用时t h,
90t=60(t),
解得t,
h=80min,故④正确;
故选:B.
【点评】本题考查一次函数的应用,从函数图象中获取解答问题的信息是解答本题的关键.
5.(2024秋 市中区期中)如图1是某湖最深处的一个截面图,湖水面下任意一点A的压强P(单位:cmHg)与其离水面的深度h(单位:m)的函数解析式为P=ah+P0,其图象如图2所示,其中P0为湖水面大气压强,a为常数且a>0,点M的坐标为(34.5,342),根据图中信息分析,下列结论正确的是( )
A.湖水面大气压强为76.0cmHg
B.函数解析式P=ah+P0中P的取值范围是P<342
C.湖水深20m处的压强为256cmHg
D.P与h的函数解析式为P=8h+66(0≤h≤34.5)
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;推理能力.
【答案】D
【分析】由图象可知,直线P=kh+P0过点(0,66)和(34.5,342).由此可得出k和P0的值,进而可判断A,D;根据实际情况可得出h的取值范围,进而可判断B;将h=20代入解析式,可求出P的值,进而可判断C.
【解答】解:由图象可知,直线P=kh+P0过点(0,66)和(34.5,342).
∴,
解得,
∴直线解析式为:P=8h+66.故D正确,符合题意;
∴青海湖水面大气压强为66.0cmHg,故A错误,不符合题意;
根据实际意义,函数解析式P=ah+P0中P的取值范围是66≤P≤342,故B错误,不符合题意;
将h=20代入解析式P=8h+66,
∴P=8×20+66=226,即青海湖水深20m处的压强为226cmHg,故C错误,不符合题意.
故选:D.
【点评】本题主要考查一次函数的实际应用,涉及一次函数的图象和性质,待定系数法等知识.关键是计算过程中需要结合实际意义.
二.填空题(共5小题)
6.(2024秋 市南区校级期中)某公司生产了A,B两款新能源电动汽车.如图,l1,l2分别表示A款,B款新能源电动汽车充满电后电池的剩余电量y(kw h)与汽车行驶路程x(km)的关系.当两款新能源电动汽车的行驶路程都是250km时,A款新能源电动汽车电池的剩余电量比B款新能源电动汽车电池的剩余电量多 10 kw h.
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】10.
【分析】利用待定系数法分别求出图象l1,l2的函数表达式,将x=250分别代入两个函数表达式求出对应的函数值并计算二者之差即可.
【解答】解:设图象l1的函数表达式为y1=k1x+b1(k1、b1为常数,且k1≠0).
将坐标(0,80)和(200,48)分别代入y1=k1x+b1,
得,
解得,
∴图象l1的函数表达式为y1x+80;
设图象l2的函数表达式为y2=k2x+b2(k2、b2为常数,且k2≠0).
将坐标(0,80)和(200,40)分别代入y2=k2x+b2,
得,
解得,
∴图象l2的函数表达式为y2x+80.
当x=250时,y1250+80=40,y2250+80=30,
40﹣30=10(kw h),
∴当两款新能源电动汽车的行驶路程都是250cm时,A款新能源电动汽车电池的剩余电量比B款新能源电动汽车电池的剩余电量多10kw h.
故答案为:10.
【点评】本题考查一次函数的应用,掌握待定系数法求函数表达式是解题的关键.
7.(2024秋 历下区期中)A,B两地相距30km,甲、乙两人沿同一条路从A地到B地.甲骑自行车以10km/h的速度先出发,1.5小时后,乙开车以40km/h的速度出发.两人之间的距离s(km)与甲出发的时间t(h)的函数关系如图所示,当乙到达B地时两人相距 7.5 km.
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】7.5.
【分析】根据路程÷速度=时间求出乙到达B地所用时间,从而求出甲骑行的时间并根据“速度×时间=路程”求出此时甲骑行的路程,进而求出两人的之间的距离即可.
【解答】解:乙到达B地所用时间为30÷40=0.75(h),
当乙到达B地时,甲骑行的时间为1.5+0.75=2.25(h),骑行的路程为10×2.25=22.5(km),
30﹣22.5=7.5(km),
∴当乙到达B地时两人相距7.5km.
故答案为:7.5.
【点评】本题考查一次函数的应用,掌握速度、时间和路程之间的数量关系是解题的关键.
8.(2024春 三门县期末)一个弹簧不挂重物时长12cm,挂上重物后伸长的长度与所挂重物的质量成正比.如果挂上1kg的物体后,弹簧伸长2cm,弹簧的总长度y cm与所挂物体的质量x kg的函数表达式是 y=12+2x .
【考点】一次函数的应用.
【专题】一次函数及其应用;应用意识.
【答案】y=12+2x.
【分析】弹簧总长=弹簧原来的长度+挂上x kg重物质量时弹簧伸长的长度,把相关数值代入即可.
【解答】解:∵挂上1kg的物体后,弹簧伸长2cm,
∴挂上x kg的物体后,弹簧伸长2x cm,
∴弹簧总长y=12+2x.
即弹簧的总长度y cm与所挂物体的质量x kg的函数表达式是y=12+2x,
故答案为:y=12+2x.
【点评】本题考查了一次函数的应用,根据实际问题列一次函数解析式,得到弹簧总长的等量关系是解决本题的关键.
9.(2024秋 龙华区期中)同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数关系是yx+32,如果某一温度的摄氏度数是5℃,那么它的华氏度数是 41 ℉.
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力.
【答案】41.
【分析】把x的值代入函数关系式计算求出y值即可.
【解答】解:当x=5时,
y5+32
=41,
故答案为:41.
【点评】本题考查一次函数的应用,理解函数值的概念并正确代入准确计算是解题的关键.
10.(2024秋 潍坊期中)火星探测车是登陆火星并进行探测的可移动探测器,为应对极端温度环境,制造火星车使用的是新型隔温材料——纳米气凝胶,该材料导热率(W/m K)与温度(℃)的关系如表:
温度(℃) 100 150 200 250 300
导热率(W/m K) 0.15 0.2 0.25 0.3 0.35
根据表格中两者的对应关系,若导热率为0.75W/m K,则温度为 700 ℃.
【考点】一次函数的应用.
【专题】一次函数及其应用;应用意识.
【答案】700.
【分析】根据表格数据可知,导热率(W/m K)与温度(℃)的函数关系为一次函数,然后用待定系数法求函数解析式,再把y=0.75代入解析式求出x的值即可.
【解答】解:根据表格数据可知,温度每增加50℃,导热率增加0.05W/m K,
∴该材料导热率(W/m K)与温度(℃)的函数关系为一次函数,
设导热率(W/m K)与温度(℃)的函数关系式为y=kx+b,
把x=100,y=0.15;x=150,y=0.2代入解析式得:,
解得:,
∴设导热率(W/m K)与温度(℃)的函数关系式为y=0.001x+0.05,
当y=0.75时,0.001x+0.05=0.75,
解得x=700,
∴当导热率为0.75W/m K时,温度为700℃,
故答案为:700.
【点评】本题考查一次函数的应用,关键是求出函数解析式.
三.解答题(共5小题)
11.(2024秋 莱西市期中)近年来,越来越多的上班族使用网上订餐服务.某外卖员上周星期目的送餐收入是200元,现以此收入为“基准”记为0,用图中的折线表示该外卖员本周每天送餐收入的变化情况.
(1)本周该外卖员星期日与星期二相比送餐收入是增多了还是减少了?变化了多少?
(2)用正号表示收入比前一天增多,负号表示收入比前一天减少,完成下表:
星期 一 二 三 四 五 六 日
收入变化(元) +10 ﹣10 +5
(3)求该外卖员本周送餐平均收入是多少元?
【考点】一次函数的应用;正数和负数.
【专题】实数;一次函数及其应用;符号意识;运算能力;应用意识.
【答案】(1)增多了,增多了40元;
(2)﹣20,+30,﹣25,+40;
(3)210元.
【分析】(1)根据图象,计算星期日的收入减星期二的收入,若结果为正,则收入增加了;若结果为0,则收入不变;若结果为负,则收入减少了;
(2)根据图象,与前一天收入的差即为收入的变化;
(3)本根据本周的总收入除以天数计算即可.
【解答】解:(1)30﹣(﹣10)=40(元).
答:本周该外卖员星期日与星期二相比送餐收入增多了,增多了40元.
(2)星期二比星期一收入的变化为﹣10﹣10=﹣20(元),
星期三比星期二收入的变化为20﹣(﹣10)=+30(元),
星期五比星期四收入的变化为﹣15﹣10=﹣25(元),
星期六比星期五收入的变化为25﹣(﹣15)=+40(元).
(3)[200×7+10+(﹣10)+20+10+(﹣15)+25+30]÷7=210(元).
答:该外卖员本周送餐平均收入是210元.
【点评】本题考查一次函数、正数和负数,掌握正数和负数相反的意义及有理数的加法运算法则是解题的关键.
12.(2024秋 市南区校级期中)如图,在平面直角坐标系xOy中,直线yx+4与x轴y轴分别交于点A,B,点D在y轴的负半轴上.若将△DAB沿直线AD折叠,点B恰好落在x轴负半轴上的点C处.
(1)求AB的长;
(2)求点C和点D的坐标;
(3)在y轴上是否存在一点P,使得S△PAB?若存在,直接写出点P的坐标;若不存在,请说明理由.
【考点】一次函数综合题.
【专题】代数几何综合题;展开与折叠;推理能力.
【答案】(1)5;
(2)点C(﹣8,0),点D(0,﹣6);
(3)存在,点P的坐标为:(0,)或(0,).
【分析】(1)对于yx+4,当x=0时,y=4,令yx+4=0,则x=﹣3,即可求解;
(2)由图象的折叠知,AC=AB=5且CD=BD,即可求解;
(3)由则S△PAB=8|yB﹣yP||8﹣yP|,即可求解.
【解答】解:(1)对于yx+4,当x=0时,y=4,
令yx+4=0,则x=﹣3,
即点A、B的坐标分别为:(﹣3,0)、(0,4),
由点A、B的坐标得,AB=5;
(2)存在,理由:
设点D(0,m),
由图象的折叠知,AC=AB=5且CD=BD,
则点C(﹣8,0),
由CD=BD得:(4﹣m)2=82+m2,
解得:m=﹣6,
即点D(0,﹣6);
(3)∵S△CODCO OD24,
则S△PAB=8|yB﹣yP||8﹣yP|,
解得:yP或,
综上,点P的坐标为:(0,)或(0,).
【点评】本题主要考查的是一次函数的综合应用,解答本题主要应用了翻折的性质,勾股定理,三角形面积公式等知识,依据勾股定理列出方程是解题的关键.
13.(2024秋 宝安区期中)暑假期间,小刚一家准备乘坐高铁前往西安旅游,计划第二天到甲、乙两个租车公司租用新能源汽车去兵马俑.甲、乙两公司收费如下,甲公司:按日收取固定租金100元,另外再按租车时间计费;乙公司:无固定租金,直接以租车时间计费,每小时的租金是40元.设租车时间为x小时,租用甲公司的车所需费用为y1元,租用乙公司的车所需费用为y2元,关系如图所示.根据以上信息,解决下列问题:
(1)直接写出y1,y2与x之间的表达式;
(2)结合图象,请你帮助小明分析选择哪家租车公司更合算.
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】(1)y1=20x+100,y2=40x;
(2)当租车时间少于5小时时,选择乙租车公司更合算;当租车时间等于5小时时,两家租车公司所需费用一样多,任选一家即可;当租车时间多于5小时时,选择甲租车公司更合算.
【分析】(1)求出甲公司每小时的租金,再分别根据“租用甲公司的车所需费用=甲公司每小时的租金×租车时间+租金”和“租用乙公司的车所需费用=乙公司每小时的租金×租车时间”写出y1,y2与x之间的表达式即可;
(2)求出两图象的交点的横坐标,再按照x的取值范围比较y1,y2的大小即可.
【解答】解:(1)∵甲公司每小时的租金为120﹣100=20(元),乙公司每小时的租金是40元,
∴y1与x之间的表达式为y1=20x+100,y2与x之间的表达式为y2=40x.
(2)当y1=y2时,得20x+100=40x,
解得x=5,
由图象可知,当x<5时,y1>y2;
当x=5时,y1=y2;
当x>5时,y1<y2,
∴当租车时间少于5小时时,选择乙租车公司更合算;当租车时间等于5小时时,两家租车公司所需费用一样多,任选一家即可;当租车时间多于5小时时,选择甲租车公司更合算.
【点评】本题考查一次函数的应用,写出y1,y2与x之间的表达式、求出两图象的交点的横坐标是解题的关键.
14.(2024秋 市南区校级期中)“漏壶”是一种古代计时器,在社会实践活动中,某小组同学根据“漏壶”的原理制作了如图①所示的液体漏壶,漏壶是由一个圆锥和一个圆柱组成的,中间连通,液体可以从圆锥容器中匀速漏到圆柱容器中,实验开始时圆柱容器中已有一部分液体.
(1)表是实验记录的圆柱体容器液面高度y(厘米)与时间x(小时)的数据:
时间x(小时) 0 1 2 3 4
圆柱体容器液面高度y(厘米) 2 6 10 14 18
在如图②所示的直角坐标系中描出如表的各点,用光滑的线连接;
(2)请根据(1)中的数据确定y与x之间的函数表达式;
(3)如果本次实验记录的开始时间是上午8:00,那么当圆柱体容器液面高度达到16厘米时是几点?
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】(1)描点并连线见解答;
(2)y=4x+2;
(3)上午11:30.
【分析】(1)描点并连线即可;
(2)利用待定系数法解答即可;
(3)将y=16代入(2)中求得的y与x之间的函数表达式,求出对应x的值并根据本次实验记录的开始时间是上午8:00计算即可.
【解答】解:(1)描点并连线如图所示:
(2)设y与x之间的函数表达式为y=kx+b(k、b为常数,且k≠0).
将坐标(0,2)和(1,6)分别代入y=kx+b,
得,
解得.
答:y与x之间的函数表达式为y=4x+2.
(3)当y=16时,得4x+2=16,
解得x=3.5,
上午8:00经过3.5小时是上午11:30.
答:如果本次实验记录的开始时间是上午8:00,那么当圆柱体容器液面高度达到16厘米时是上午11:30.
【点评】本题考查一次函数的应用,掌握待定系数法求函数关系式是解题的关键.
15.(2024秋 罗湖区校级期中)我校将举办一年一度的秋季运动会,需要采购一批某品牌的乒乓球拍和配套的乒乓球,一副球拍标价80元,一盒球标价25元.体育商店提供了两种优惠方案,具体如下:
方案甲:买一副乒乓球拍送一盒乒乓球,其余乒乓球按原价出售;
方案乙:按购买金额打9折付款.
学校欲购买这种乒乓球拍10副,乒乓球x(x 10)盒.
(1)请直接写出两种优惠办法实际付款金额y甲(元),y乙(元)与x(盒)之间的函数关系式.
(2)如果学校提供经费为1800元,选择哪个方案能购买更多乒乓球?
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力.
【答案】(1)y甲=25x+550,y乙=22.5x+720;(2)校提供经费为1800元,选择方案甲能购买更多乒乓球.
【分析】(1)根据购买费用=单价×数量,建立关系表示的函数关系式即可.
(2)将y=1800分别代入两个解析式中,计算求解,然后比较作答即可.
【解答】解:(1)由题意得:y甲=10×80+25(x﹣10)=25x+550,
y乙=25×0.9x+80×0.9×10=22.5x+720,
(2)由(1)得:y甲=25x+550,y乙=22.5x+720,
当y甲=1800元时,1800=25x+550,当y乙=1800元时,1800=22.5x+720,
解得:x甲=50,x乙=48,
∵50>48,
∴学校提供经费为1800元,选择方案甲能购买更多乒乓球.
【点评】本题考查了一次函数的应用.熟练掌握一次函数的应用是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.夯实基础 一次函数的应用
一.选择题(共5小题)
1.(2024秋 雁塔区校级期中)在一定范围内,弹簧的受力和伸长长度成正比.某次数学实验中,同学们记录了同一根弹簧的长度y(cm)和所挂物体质量x(kg)(0≤x≤12)的对应数据如表(部分)所示,下列说法中不正确的是( )
x(kg) 1 2 3 4 …
y(cm) 10.5 11 11.5 12 …
A.x,y都是变量,y是x的一次函数
B.弹簧不挂物体时的长度是10cm
C.当所挂物体的质量为10kg时,弹簧长度是15cm
D.物体质量由4kg增加到7kg,弹簧的长度增加1cm
2.(2024秋 深圳期中)甲、乙两人同起点同方向出发,匀速步行3000米,先到终点的人原地休息.已知甲先出发3分钟,甲、乙两人之间的距离y(米)与甲出发的时间t(分)之间的关系如图所示,则下列说法正确是( )
A.甲步行的平均速度为32米/分
B.乙步行的平均速度为20米/分
C.当t=30时,乙到达终点
D.乙比甲提前4.5分钟到达终点
3.(2024 青山区模拟)漏刻是我国古代的一种计时工具,据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用,小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现水位h(cm)是时间t(min)的一次函数,如下表是小明记录的部分数据,当时间t为10时,对应的高度h为( )
t(min) … 0 1 2 3 …
h(cm) … 0.7 1.1 1.5 1.9 …
A.3.3 B.3.65 C.3.9 D.4.7
4.(2024秋 荥阳市期中)甲、乙两车从A地出发,沿同一路线驶向B地,甲车先出发匀速驶向B地,40min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了50km/h,结果与甲车同时到达B地.甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:
①a=4.5;
②甲的速度是60km/h;
③乙刚开始的速度是80km/h;
④乙出发第一次追上甲用时80min.
其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
5.(2024秋 市中区期中)如图1是某湖最深处的一个截面图,湖水面下任意一点A的压强P(单位:cmHg)与其离水面的深度h(单位:m)的函数解析式为P=ah+P0,其图象如图2所示,其中P0为湖水面大气压强,a为常数且a>0,点M的坐标为(34.5,342),根据图中信息分析,下列结论正确的是( )
A.湖水面大气压强为76.0cmHg
B.函数解析式P=ah+P0中P的取值范围是P<342
C.湖水深20m处的压强为256cmHg
D.P与h的函数解析式为P=8h+66(0≤h≤34.5)
二.填空题(共5小题)
6.(2024秋 市南区校级期中)某公司生产了A,B两款新能源电动汽车.如图,l1,l2分别表示A款,B款新能源电动汽车充满电后电池的剩余电量y(kw h)与汽车行驶路程x(km)的关系.当两款新能源电动汽车的行驶路程都是250km时,A款新能源电动汽车电池的剩余电量比B款新能源电动汽车电池的剩余电量多 kw h.
7.(2024秋 历下区期中)A,B两地相距30km,甲、乙两人沿同一条路从A地到B地.甲骑自行车以10km/h的速度先出发,1.5小时后,乙开车以40km/h的速度出发.两人之间的距离s(km)与甲出发的时间t(h)的函数关系如图所示,当乙到达B地时两人相距 km.
8.(2024春 三门县期末)一个弹簧不挂重物时长12cm,挂上重物后伸长的长度与所挂重物的质量成正比.如果挂上1kg的物体后,弹簧伸长2cm,弹簧的总长度y cm与所挂物体的质量x kg的函数表达式是 .
9.(2024秋 龙华区期中)同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数关系是yx+32,如果某一温度的摄氏度数是5℃,那么它的华氏度数是 ℉.
10.(2024秋 潍坊期中)火星探测车是登陆火星并进行探测的可移动探测器,为应对极端温度环境,制造火星车使用的是新型隔温材料——纳米气凝胶,该材料导热率(W/m K)与温度(℃)的关系如表:
温度(℃) 100 150 200 250 300
导热率(W/m K) 0.15 0.2 0.25 0.3 0.35
根据表格中两者的对应关系,若导热率为0.75W/m K,则温度为 ℃.
三.解答题(共5小题)
11.(2024秋 莱西市期中)近年来,越来越多的上班族使用网上订餐服务.某外卖员上周星期目的送餐收入是200元,现以此收入为“基准”记为0,用图中的折线表示该外卖员本周每天送餐收入的变化情况.
(1)本周该外卖员星期日与星期二相比送餐收入是增多了还是减少了?变化了多少?
(2)用正号表示收入比前一天增多,负号表示收入比前一天减少,完成下表:
星期 一 二 三 四 五 六 日
收入变化(元) +10 ﹣10 +5
(3)求该外卖员本周送餐平均收入是多少元?
12.(2024秋 市南区校级期中)如图,在平面直角坐标系xOy中,直线yx+4与x轴y轴分别交于点A,B,点D在y轴的负半轴上.若将△DAB沿直线AD折叠,点B恰好落在x轴负半轴上的点C处.
(1)求AB的长;
(2)求点C和点D的坐标;
(3)在y轴上是否存在一点P,使得S△PAB?若存在,直接写出点P的坐标;若不存在,请说明理由.
13.(2024秋 宝安区期中)暑假期间,小刚一家准备乘坐高铁前往西安旅游,计划第二天到甲、乙两个租车公司租用新能源汽车去兵马俑.甲、乙两公司收费如下,甲公司:按日收取固定租金100元,另外再按租车时间计费;乙公司:无固定租金,直接以租车时间计费,每小时的租金是40元.设租车时间为x小时,租用甲公司的车所需费用为y1元,租用乙公司的车所需费用为y2元,关系如图所示.根据以上信息,解决下列问题:
(1)直接写出y1,y2与x之间的表达式;
(2)结合图象,请你帮助小明分析选择哪家租车公司更合算.
14.(2024秋 市南区校级期中)“漏壶”是一种古代计时器,在社会实践活动中,某小组同学根据“漏壶”的原理制作了如图①所示的液体漏壶,漏壶是由一个圆锥和一个圆柱组成的,中间连通,液体可以从圆锥容器中匀速漏到圆柱容器中,实验开始时圆柱容器中已有一部分液体.
(1)表是实验记录的圆柱体容器液面高度y(厘米)与时间x(小时)的数据:
时间x(小时) 0 1 2 3 4
圆柱体容器液面高度y(厘米) 2 6 10 14 18
在如图②所示的直角坐标系中描出如表的各点,用光滑的线连接;
(2)请根据(1)中的数据确定y与x之间的函数表达式;
(3)如果本次实验记录的开始时间是上午8:00,那么当圆柱体容器液面高度达到16厘米时是几点?
15.(2024秋 罗湖区校级期中)我校将举办一年一度的秋季运动会,需要采购一批某品牌的乒乓球拍和配套的乒乓球,一副球拍标价80元,一盒球标价25元.体育商店提供了两种优惠方案,具体如下:
方案甲:买一副乒乓球拍送一盒乒乓球,其余乒乓球按原价出售;
方案乙:按购买金额打9折付款.
学校欲购买这种乒乓球拍10副,乒乓球x(x 10)盒.
(1)请直接写出两种优惠办法实际付款金额y甲(元),y乙(元)与x(盒)之间的函数关系式.
(2)如果学校提供经费为1800元,选择哪个方案能购买更多乒乓球?
预习衔接.夯实基础 一次函数的应用
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 雁塔区校级期中)在一定范围内,弹簧的受力和伸长长度成正比.某次数学实验中,同学们记录了同一根弹簧的长度y(cm)和所挂物体质量x(kg)(0≤x≤12)的对应数据如表(部分)所示,下列说法中不正确的是( )
x(kg) 1 2 3 4 …
y(cm) 10.5 11 11.5 12 …
A.x,y都是变量,y是x的一次函数
B.弹簧不挂物体时的长度是10cm
C.当所挂物体的质量为10kg时,弹簧长度是15cm
D.物体质量由4kg增加到7kg,弹簧的长度增加1cm
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】D
【分析】A.根据变量的定义及“所挂物体的质量x增加1kg,弹簧的长度y伸长0.5cm”判断即可;
B.利用待定系数法求出y与x之间的函数关系式,将x=0代入该函数求出对应y的值即可;
C.将x=10代入该函数求出对应y的值即可;
D.分别将x=4和x=7代入y与x之间的函数关系式,求出对应的y值并求差即可.
【解答】解:∵x,y都是变量,且所挂物体的质量x增加1kg,弹簧的长度y伸长0.5cm,
∴弹簧的长度y和所挂物体质量x的一次函数,
∴A正确,不符合题意;
设y与x之间的函数关系式为y=kx+b(k、b为常数,且k≠0),
把x=2,y=11和x=4,y=12分别代入y=kx+b,
得,
解得,
∴y与x之间的函数关系式为y=0.5x+10,
当x=0时,y=10,
∴弹簧不挂物体时的长度是10cm,
∴B正确,不符合题意;
当x=10时,y=0.5×10+10=15,
∴当所挂物体的质量为10kg时,弹簧长度是15cm,
∴C正确,不符合题意;
当x=4时,y=0.5×4+10=12,
当x=7时,y=0.5×7+10=13.5,
13.5﹣12=1.5(cm),
∴物体质量由4kg增加到7kg,弹簧的长度增加1.5cm,
∴D不正确,符合题意.
故选:D.
【点评】本题考查一次函数的应用,掌握变量的定义、一次函数的判断方法是解题的关键.
2.(2024秋 深圳期中)甲、乙两人同起点同方向出发,匀速步行3000米,先到终点的人原地休息.已知甲先出发3分钟,甲、乙两人之间的距离y(米)与甲出发的时间t(分)之间的关系如图所示,则下列说法正确是( )
A.甲步行的平均速度为32米/分
B.乙步行的平均速度为20米/分
C.当t=30时,乙到达终点
D.乙比甲提前4.5分钟到达终点
【考点】一次函数的应用.
【专题】一次函数及其应用;应用意识.
【答案】D
【分析】根据函数图象,求出甲、乙的速度,再求出它们到达终点的时间即可求解.
【解答】解:由图可得,甲的速度为240÷3=80(米/分),故选项A不符合题意;
设乙的速度为x米/分,
由图可得,(15﹣3)x=240+80×(15﹣3),
解得x=100,
∴乙的速度为100米/分,故选项B不符合题意;
∴甲到达终点的时间为3000÷80=37.5(分钟),
乙达到终点的时间为3000÷100=30(分钟),
30+3=33(分钟),
即当t=33时,乙到达终点,故选项C不符合题意;
∵甲先出发3分钟,
∴乙先到终点原地休息了37.5﹣3﹣30=4.5(分钟),
即乙比甲提前4.5分钟到达终点.
故说法正确是D.
故选:D.
【点评】本题考查了一次函数的应用,看懂函数的图象是解题的关键.
3.(2024 青山区模拟)漏刻是我国古代的一种计时工具,据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用,小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现水位h(cm)是时间t(min)的一次函数,如下表是小明记录的部分数据,当时间t为10时,对应的高度h为( )
t(min) … 0 1 2 3 …
h(cm) … 0.7 1.1 1.5 1.9 …
A.3.3 B.3.65 C.3.9 D.4.7
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力.
【答案】D
【分析】设水位h(cm)与时间t(min)的关系式h=kt+b,用待定系数法求出解析式即可.
【解答】解:设水位h(cm)与时间t(min)的关系式h=kt+b,
把t=0,h=0.7和t=1,h=1.1代入表中数据得:,
解得:,
∴水位h(cm)与时间t(min)的关系式h=0.4t+0.7.
把t=10代入h=0.4t+0.7中,得h=0.4×10+0.7=4.7,
故选:D.
【点评】本题考查一次函数的知识,熟练掌握待定系数法求解析式是解题的关键.
4.(2024秋 荥阳市期中)甲、乙两车从A地出发,沿同一路线驶向B地,甲车先出发匀速驶向B地,40min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了50km/h,结果与甲车同时到达B地.甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:
①a=4.5;
②甲的速度是60km/h;
③乙刚开始的速度是80km/h;
④乙出发第一次追上甲用时80min.
其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
【考点】一次函数的应用.
【专题】一次函数及其应用;几何直观;运算能力;应用意识.
【答案】B
【分析】根据题意和函数图象中的数据,可以计算出各个小题中的结论是否正确,从而可以解答本题.
【解答】解:由图象可得,
a=4+0.5=4.5,故①正确;
甲的速度是460÷(7)=60(km/h),故②正确;
设乙刚开始的速度是v km/h,则后来的速度为(v﹣50)km/h,
4v+(7﹣4.5)×(v﹣50)=460,
解得v=90,故③错误;
设乙出发第一次追上甲用时t h,
90t=60(t),
解得t,
h=80min,故④正确;
故选:B.
【点评】本题考查一次函数的应用,从函数图象中获取解答问题的信息是解答本题的关键.
5.(2024秋 市中区期中)如图1是某湖最深处的一个截面图,湖水面下任意一点A的压强P(单位:cmHg)与其离水面的深度h(单位:m)的函数解析式为P=ah+P0,其图象如图2所示,其中P0为湖水面大气压强,a为常数且a>0,点M的坐标为(34.5,342),根据图中信息分析,下列结论正确的是( )
A.湖水面大气压强为76.0cmHg
B.函数解析式P=ah+P0中P的取值范围是P<342
C.湖水深20m处的压强为256cmHg
D.P与h的函数解析式为P=8h+66(0≤h≤34.5)
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;推理能力.
【答案】D
【分析】由图象可知,直线P=kh+P0过点(0,66)和(34.5,342).由此可得出k和P0的值,进而可判断A,D;根据实际情况可得出h的取值范围,进而可判断B;将h=20代入解析式,可求出P的值,进而可判断C.
【解答】解:由图象可知,直线P=kh+P0过点(0,66)和(34.5,342).
∴,
解得,
∴直线解析式为:P=8h+66.故D正确,符合题意;
∴青海湖水面大气压强为66.0cmHg,故A错误,不符合题意;
根据实际意义,函数解析式P=ah+P0中P的取值范围是66≤P≤342,故B错误,不符合题意;
将h=20代入解析式P=8h+66,
∴P=8×20+66=226,即青海湖水深20m处的压强为226cmHg,故C错误,不符合题意.
故选:D.
【点评】本题主要考查一次函数的实际应用,涉及一次函数的图象和性质,待定系数法等知识.关键是计算过程中需要结合实际意义.
二.填空题(共5小题)
6.(2024秋 市南区校级期中)某公司生产了A,B两款新能源电动汽车.如图,l1,l2分别表示A款,B款新能源电动汽车充满电后电池的剩余电量y(kw h)与汽车行驶路程x(km)的关系.当两款新能源电动汽车的行驶路程都是250km时,A款新能源电动汽车电池的剩余电量比B款新能源电动汽车电池的剩余电量多 10 kw h.
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】10.
【分析】利用待定系数法分别求出图象l1,l2的函数表达式,将x=250分别代入两个函数表达式求出对应的函数值并计算二者之差即可.
【解答】解:设图象l1的函数表达式为y1=k1x+b1(k1、b1为常数,且k1≠0).
将坐标(0,80)和(200,48)分别代入y1=k1x+b1,
得,
解得,
∴图象l1的函数表达式为y1x+80;
设图象l2的函数表达式为y2=k2x+b2(k2、b2为常数,且k2≠0).
将坐标(0,80)和(200,40)分别代入y2=k2x+b2,
得,
解得,
∴图象l2的函数表达式为y2x+80.
当x=250时,y1250+80=40,y2250+80=30,
40﹣30=10(kw h),
∴当两款新能源电动汽车的行驶路程都是250cm时,A款新能源电动汽车电池的剩余电量比B款新能源电动汽车电池的剩余电量多10kw h.
故答案为:10.
【点评】本题考查一次函数的应用,掌握待定系数法求函数表达式是解题的关键.
7.(2024秋 历下区期中)A,B两地相距30km,甲、乙两人沿同一条路从A地到B地.甲骑自行车以10km/h的速度先出发,1.5小时后,乙开车以40km/h的速度出发.两人之间的距离s(km)与甲出发的时间t(h)的函数关系如图所示,当乙到达B地时两人相距 7.5 km.
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】7.5.
【分析】根据路程÷速度=时间求出乙到达B地所用时间,从而求出甲骑行的时间并根据“速度×时间=路程”求出此时甲骑行的路程,进而求出两人的之间的距离即可.
【解答】解:乙到达B地所用时间为30÷40=0.75(h),
当乙到达B地时,甲骑行的时间为1.5+0.75=2.25(h),骑行的路程为10×2.25=22.5(km),
30﹣22.5=7.5(km),
∴当乙到达B地时两人相距7.5km.
故答案为:7.5.
【点评】本题考查一次函数的应用,掌握速度、时间和路程之间的数量关系是解题的关键.
8.(2024春 三门县期末)一个弹簧不挂重物时长12cm,挂上重物后伸长的长度与所挂重物的质量成正比.如果挂上1kg的物体后,弹簧伸长2cm,弹簧的总长度y cm与所挂物体的质量x kg的函数表达式是 y=12+2x .
【考点】一次函数的应用.
【专题】一次函数及其应用;应用意识.
【答案】y=12+2x.
【分析】弹簧总长=弹簧原来的长度+挂上x kg重物质量时弹簧伸长的长度,把相关数值代入即可.
【解答】解:∵挂上1kg的物体后,弹簧伸长2cm,
∴挂上x kg的物体后,弹簧伸长2x cm,
∴弹簧总长y=12+2x.
即弹簧的总长度y cm与所挂物体的质量x kg的函数表达式是y=12+2x,
故答案为:y=12+2x.
【点评】本题考查了一次函数的应用,根据实际问题列一次函数解析式,得到弹簧总长的等量关系是解决本题的关键.
9.(2024秋 龙华区期中)同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数关系是yx+32,如果某一温度的摄氏度数是5℃,那么它的华氏度数是 41 ℉.
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力.
【答案】41.
【分析】把x的值代入函数关系式计算求出y值即可.
【解答】解:当x=5时,
y5+32
=41,
故答案为:41.
【点评】本题考查一次函数的应用,理解函数值的概念并正确代入准确计算是解题的关键.
10.(2024秋 潍坊期中)火星探测车是登陆火星并进行探测的可移动探测器,为应对极端温度环境,制造火星车使用的是新型隔温材料——纳米气凝胶,该材料导热率(W/m K)与温度(℃)的关系如表:
温度(℃) 100 150 200 250 300
导热率(W/m K) 0.15 0.2 0.25 0.3 0.35
根据表格中两者的对应关系,若导热率为0.75W/m K,则温度为 700 ℃.
【考点】一次函数的应用.
【专题】一次函数及其应用;应用意识.
【答案】700.
【分析】根据表格数据可知,导热率(W/m K)与温度(℃)的函数关系为一次函数,然后用待定系数法求函数解析式,再把y=0.75代入解析式求出x的值即可.
【解答】解:根据表格数据可知,温度每增加50℃,导热率增加0.05W/m K,
∴该材料导热率(W/m K)与温度(℃)的函数关系为一次函数,
设导热率(W/m K)与温度(℃)的函数关系式为y=kx+b,
把x=100,y=0.15;x=150,y=0.2代入解析式得:,
解得:,
∴设导热率(W/m K)与温度(℃)的函数关系式为y=0.001x+0.05,
当y=0.75时,0.001x+0.05=0.75,
解得x=700,
∴当导热率为0.75W/m K时,温度为700℃,
故答案为:700.
【点评】本题考查一次函数的应用,关键是求出函数解析式.
三.解答题(共5小题)
11.(2024秋 莱西市期中)近年来,越来越多的上班族使用网上订餐服务.某外卖员上周星期目的送餐收入是200元,现以此收入为“基准”记为0,用图中的折线表示该外卖员本周每天送餐收入的变化情况.
(1)本周该外卖员星期日与星期二相比送餐收入是增多了还是减少了?变化了多少?
(2)用正号表示收入比前一天增多,负号表示收入比前一天减少,完成下表:
星期 一 二 三 四 五 六 日
收入变化(元) +10 ﹣10 +5
(3)求该外卖员本周送餐平均收入是多少元?
【考点】一次函数的应用;正数和负数.
【专题】实数;一次函数及其应用;符号意识;运算能力;应用意识.
【答案】(1)增多了,增多了40元;
(2)﹣20,+30,﹣25,+40;
(3)210元.
【分析】(1)根据图象,计算星期日的收入减星期二的收入,若结果为正,则收入增加了;若结果为0,则收入不变;若结果为负,则收入减少了;
(2)根据图象,与前一天收入的差即为收入的变化;
(3)本根据本周的总收入除以天数计算即可.
【解答】解:(1)30﹣(﹣10)=40(元).
答:本周该外卖员星期日与星期二相比送餐收入增多了,增多了40元.
(2)星期二比星期一收入的变化为﹣10﹣10=﹣20(元),
星期三比星期二收入的变化为20﹣(﹣10)=+30(元),
星期五比星期四收入的变化为﹣15﹣10=﹣25(元),
星期六比星期五收入的变化为25﹣(﹣15)=+40(元).
(3)[200×7+10+(﹣10)+20+10+(﹣15)+25+30]÷7=210(元).
答:该外卖员本周送餐平均收入是210元.
【点评】本题考查一次函数、正数和负数,掌握正数和负数相反的意义及有理数的加法运算法则是解题的关键.
12.(2024秋 市南区校级期中)如图,在平面直角坐标系xOy中,直线yx+4与x轴y轴分别交于点A,B,点D在y轴的负半轴上.若将△DAB沿直线AD折叠,点B恰好落在x轴负半轴上的点C处.
(1)求AB的长;
(2)求点C和点D的坐标;
(3)在y轴上是否存在一点P,使得S△PAB?若存在,直接写出点P的坐标;若不存在,请说明理由.
【考点】一次函数综合题.
【专题】代数几何综合题;展开与折叠;推理能力.
【答案】(1)5;
(2)点C(﹣8,0),点D(0,﹣6);
(3)存在,点P的坐标为:(0,)或(0,).
【分析】(1)对于yx+4,当x=0时,y=4,令yx+4=0,则x=﹣3,即可求解;
(2)由图象的折叠知,AC=AB=5且CD=BD,即可求解;
(3)由则S△PAB=8|yB﹣yP||8﹣yP|,即可求解.
【解答】解:(1)对于yx+4,当x=0时,y=4,
令yx+4=0,则x=﹣3,
即点A、B的坐标分别为:(﹣3,0)、(0,4),
由点A、B的坐标得,AB=5;
(2)存在,理由:
设点D(0,m),
由图象的折叠知,AC=AB=5且CD=BD,
则点C(﹣8,0),
由CD=BD得:(4﹣m)2=82+m2,
解得:m=﹣6,
即点D(0,﹣6);
(3)∵S△CODCO OD24,
则S△PAB=8|yB﹣yP||8﹣yP|,
解得:yP或,
综上,点P的坐标为:(0,)或(0,).
【点评】本题主要考查的是一次函数的综合应用,解答本题主要应用了翻折的性质,勾股定理,三角形面积公式等知识,依据勾股定理列出方程是解题的关键.
13.(2024秋 宝安区期中)暑假期间,小刚一家准备乘坐高铁前往西安旅游,计划第二天到甲、乙两个租车公司租用新能源汽车去兵马俑.甲、乙两公司收费如下,甲公司:按日收取固定租金100元,另外再按租车时间计费;乙公司:无固定租金,直接以租车时间计费,每小时的租金是40元.设租车时间为x小时,租用甲公司的车所需费用为y1元,租用乙公司的车所需费用为y2元,关系如图所示.根据以上信息,解决下列问题:
(1)直接写出y1,y2与x之间的表达式;
(2)结合图象,请你帮助小明分析选择哪家租车公司更合算.
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】(1)y1=20x+100,y2=40x;
(2)当租车时间少于5小时时,选择乙租车公司更合算;当租车时间等于5小时时,两家租车公司所需费用一样多,任选一家即可;当租车时间多于5小时时,选择甲租车公司更合算.
【分析】(1)求出甲公司每小时的租金,再分别根据“租用甲公司的车所需费用=甲公司每小时的租金×租车时间+租金”和“租用乙公司的车所需费用=乙公司每小时的租金×租车时间”写出y1,y2与x之间的表达式即可;
(2)求出两图象的交点的横坐标,再按照x的取值范围比较y1,y2的大小即可.
【解答】解:(1)∵甲公司每小时的租金为120﹣100=20(元),乙公司每小时的租金是40元,
∴y1与x之间的表达式为y1=20x+100,y2与x之间的表达式为y2=40x.
(2)当y1=y2时,得20x+100=40x,
解得x=5,
由图象可知,当x<5时,y1>y2;
当x=5时,y1=y2;
当x>5时,y1<y2,
∴当租车时间少于5小时时,选择乙租车公司更合算;当租车时间等于5小时时,两家租车公司所需费用一样多,任选一家即可;当租车时间多于5小时时,选择甲租车公司更合算.
【点评】本题考查一次函数的应用,写出y1,y2与x之间的表达式、求出两图象的交点的横坐标是解题的关键.
14.(2024秋 市南区校级期中)“漏壶”是一种古代计时器,在社会实践活动中,某小组同学根据“漏壶”的原理制作了如图①所示的液体漏壶,漏壶是由一个圆锥和一个圆柱组成的,中间连通,液体可以从圆锥容器中匀速漏到圆柱容器中,实验开始时圆柱容器中已有一部分液体.
(1)表是实验记录的圆柱体容器液面高度y(厘米)与时间x(小时)的数据:
时间x(小时) 0 1 2 3 4
圆柱体容器液面高度y(厘米) 2 6 10 14 18
在如图②所示的直角坐标系中描出如表的各点,用光滑的线连接;
(2)请根据(1)中的数据确定y与x之间的函数表达式;
(3)如果本次实验记录的开始时间是上午8:00,那么当圆柱体容器液面高度达到16厘米时是几点?
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】(1)描点并连线见解答;
(2)y=4x+2;
(3)上午11:30.
【分析】(1)描点并连线即可;
(2)利用待定系数法解答即可;
(3)将y=16代入(2)中求得的y与x之间的函数表达式,求出对应x的值并根据本次实验记录的开始时间是上午8:00计算即可.
【解答】解:(1)描点并连线如图所示:
(2)设y与x之间的函数表达式为y=kx+b(k、b为常数,且k≠0).
将坐标(0,2)和(1,6)分别代入y=kx+b,
得,
解得.
答:y与x之间的函数表达式为y=4x+2.
(3)当y=16时,得4x+2=16,
解得x=3.5,
上午8:00经过3.5小时是上午11:30.
答:如果本次实验记录的开始时间是上午8:00,那么当圆柱体容器液面高度达到16厘米时是上午11:30.
【点评】本题考查一次函数的应用,掌握待定系数法求函数关系式是解题的关键.
15.(2024秋 罗湖区校级期中)我校将举办一年一度的秋季运动会,需要采购一批某品牌的乒乓球拍和配套的乒乓球,一副球拍标价80元,一盒球标价25元.体育商店提供了两种优惠方案,具体如下:
方案甲:买一副乒乓球拍送一盒乒乓球,其余乒乓球按原价出售;
方案乙:按购买金额打9折付款.
学校欲购买这种乒乓球拍10副,乒乓球x(x 10)盒.
(1)请直接写出两种优惠办法实际付款金额y甲(元),y乙(元)与x(盒)之间的函数关系式.
(2)如果学校提供经费为1800元,选择哪个方案能购买更多乒乓球?
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力.
【答案】(1)y甲=25x+550,y乙=22.5x+720;(2)校提供经费为1800元,选择方案甲能购买更多乒乓球.
【分析】(1)根据购买费用=单价×数量,建立关系表示的函数关系式即可.
(2)将y=1800分别代入两个解析式中,计算求解,然后比较作答即可.
【解答】解:(1)由题意得:y甲=10×80+25(x﹣10)=25x+550,
y乙=25×0.9x+80×0.9×10=22.5x+720,
(2)由(1)得:y甲=25x+550,y乙=22.5x+720,
当y甲=1800元时,1800=25x+550,当y乙=1800元时,1800=22.5x+720,
解得:x甲=50,x乙=48,
∵50>48,
∴学校提供经费为1800元,选择方案甲能购买更多乒乓球.
【点评】本题考查了一次函数的应用.熟练掌握一次函数的应用是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
