4.3相似多边形(预习衔接.夯实基础.含解析)-2025-2026学年九年级上册数学北师大版
文档属性
| 名称 | 4.3相似多边形(预习衔接.夯实基础.含解析)-2025-2026学年九年级上册数学北师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 576.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 21:02:07 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
预习衔接.夯实基础 相似多边形
一.选择题(共5小题)
1.(2024秋 雁塔区校级期中)如图1是古希腊时期的巴台农神庙,把图1中用虚线表示的矩形画成图2矩形ABCD,当以矩形ABCD的宽AB为边作正方形ABEF时,惊奇地发现矩形CDFE与矩形ABCD相似,则等于( )
A. B. C. D.
2.(2024秋 松江区期中)下列图形一定是相似图形的是( )
A.两个等腰三角形
B.两个面积相等的三角形
C.两个正方形
D.两个菱形
3.(2024秋 崂山区期中)某学校致力于劳动教育的探索与实践,在校内设立了“田园风光”和“耘梦园”两个相似的矩形劳动场所,它们的相似比是1:2.若两个劳动场所种植相同品种的蔬菜,在每平方米所需农资成本(主要包括化肥、农药以及灌溉用水)不变的情况下,“田园风光”的农资成本为200元,则“耘梦园”的农资成本为( )
A.800元 B.400元 C.100元 D.50元
4.(2024 连云港)下列网格中各个小正方形的边长均为1,阴影部分图形分别记作甲、乙、丙、丁,其中是相似形的为( )
A.甲和乙 B.乙和丁 C.甲和丙 D.甲和丁
5.(2024秋 阳谷县期末)如图是杭州第19届亚运会的吉祥物“琮琮”,代表的是世界遗产良渚古城遗址,名字来源于文物玉琮.琮琮全身以黄色调为主,头部刻有“饕餮纹”,展示给人们一种不屈不挠、坚强刚毅的精神.文旅部门将选定的“琮琮”形象图通过放大或缩小放置于不同的宣传版面上,这体现了数学中的( )
A.图形的平移 B.图形的轴对称
C.图形的相似 D.图形的旋转
二.填空题(共5小题)
6.(2024秋 西安期中)如图,五边形ABCDE∽五边形A'B'C'D'E',它们的相似比为3:4.已知BC=4.8cm,则B'C'= cm.
7.(2024秋 宜兴市期中)两个相似多边形的相似比为1:4,则它们的面积的比为 .
8.(2024秋 乐清市校级期中)两个相似五边形,一组对应边的长分别为2cm和3cm,若它们的面积之和为65cm2,则较小五边形的面积是 .
9.(2024秋 新城区期中)五边形ABCDE∽五边形A′B′C′D′E′,且它们的相似比为1:3.若五边形ABCDE的面积为6,则五边形A′B′C′D′E′的面积为 .
10.(2024秋 郏县期末)书画经装裱后更便于收藏.如图,ABCD为长90cm、宽30cm的矩形,装裱后整幅画为矩形A'B'C'D',两矩形的对应边互相平行,且AB与A'B'的距离、CD与C′D′的距离都等于4cm.当AD与A'D'的距离、BC与B′C′距离都等于a cm,且矩形ABCD∽矩形A'B'C'D',整幅书画最美观此时,a的值为 .
三.解答题(共5小题)
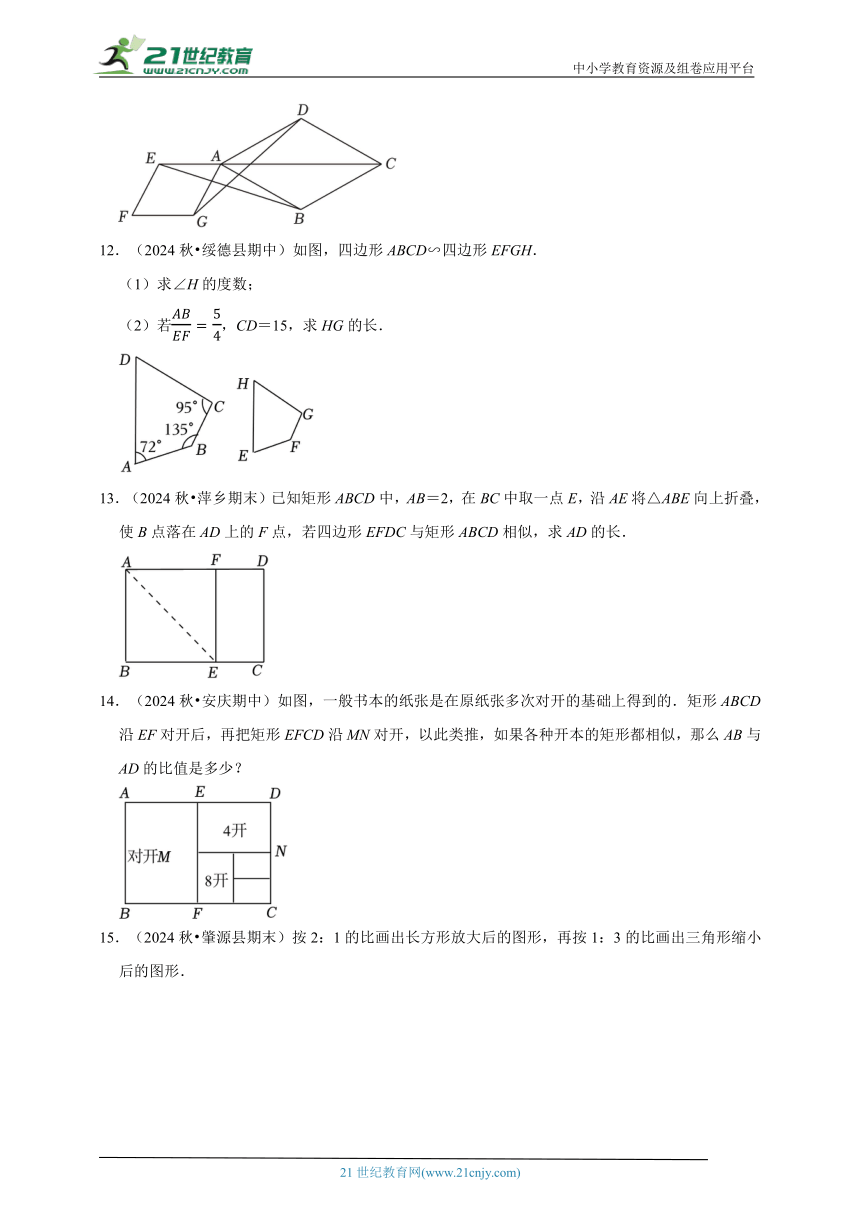
11.(2024秋 驿城区期中)如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,相似比是:2,连接EB,GD.
(1)求证:EB=GD;
(2)若∠DAB=60°,AB=2,求GD的长.
12.(2024秋 绥德县期中)如图,四边形ABCD∽四边形EFGH.
(1)求∠H的度数;
(2)若,CD=15,求HG的长.
13.(2024秋 萍乡期末)已知矩形ABCD中,AB=2,在BC中取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,求AD的长.
14.(2024秋 安庆期中)如图,一般书本的纸张是在原纸张多次对开的基础上得到的.矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,以此类推,如果各种开本的矩形都相似,那么AB与AD的比值是多少?
15.(2024秋 肇源县期末)按2:1的比画出长方形放大后的图形,再按1:3的比画出三角形缩小后的图形.
预习衔接.夯实基础 相似多边形
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 雁塔区校级期中)如图1是古希腊时期的巴台农神庙,把图1中用虚线表示的矩形画成图2矩形ABCD,当以矩形ABCD的宽AB为边作正方形ABEF时,惊奇地发现矩形CDFE与矩形ABCD相似,则等于( )
A. B. C. D.
【考点】相似多边形的性质;矩形的性质;正方形的性质.
【专题】图形的相似;推理能力.
【答案】B
【分析】根据相似多边形的对应边的比相等列出算式,解方程得到答案.
【解答】解:设EC=a,BE=b,则BC=a+b,
∵矩形CDFE∽矩形DABC,
∴,即,
整理得:a2+ab﹣b2=0,
∴()21=0,
解得:(负值舍去),
故选:B.
【点评】本题考查的是相似多边形的性质、熟记相似多边形的对应边成比例是解题的关键.
2.(2024秋 松江区期中)下列图形一定是相似图形的是( )
A.两个等腰三角形
B.两个面积相等的三角形
C.两个正方形
D.两个菱形
【考点】相似图形.
【专题】图形的相似;推理能力.
【答案】C
【分析】根据相似三角形的判定方法进行判断.
【解答】解:A、两个等腰三角形不一定相似,不符合题意;
B、两个面积相等的三角形不一定相似,不符合题意;
C、两个正方形一定相似,符合题意;
D、两个菱形不一定相似,不符合题意.
故选:C.
【点评】本题考查了相似图形:把形状相同的图形称为相似图形.
3.(2024秋 崂山区期中)某学校致力于劳动教育的探索与实践,在校内设立了“田园风光”和“耘梦园”两个相似的矩形劳动场所,它们的相似比是1:2.若两个劳动场所种植相同品种的蔬菜,在每平方米所需农资成本(主要包括化肥、农药以及灌溉用水)不变的情况下,“田园风光”的农资成本为200元,则“耘梦园”的农资成本为( )
A.800元 B.400元 C.100元 D.50元
【考点】相似多边形的性质.
【专题】图形的相似;应用意识.
【答案】A
【分析】根据相似多边形的性质求出“田园风光”和“耘梦园”两个相似的矩形劳动场所的面积比,再计算农资成本即可.
【解答】解:∵“田园风光”和“耘梦园”两个相似的矩形劳动场所,它们的相似比是1:2,
∴“田园风光”和“耘梦园”两个相似的矩形劳动场所的面积比为1:4,
∵“田园风光”的农资成本为200元,
∴“耘梦园”的农资成本为:200×4=800(元).
故选:A.
【点评】本题考查了相似多边形的性质,解题的关键是掌握相似多边形的面积比等于相似比的平方.
4.(2024 连云港)下列网格中各个小正方形的边长均为1,阴影部分图形分别记作甲、乙、丙、丁,其中是相似形的为( )
A.甲和乙 B.乙和丁 C.甲和丙 D.甲和丁
【考点】相似图形.
【专题】图形的相似;推理能力.
【答案】D
【分析】如果两个多边形的对应角相等,对应边的比相等,则这两个多边形是相似多边形.
【解答】解:观察可得:甲和丁对应角相等,对应边成比例,且形状相同,大小不同,
故选:D.
【点评】本题主要考查了相似多边形的性质,相似多边形的性质为:①对应角相等;②对应边的比相等.
5.(2024秋 阳谷县期末)如图是杭州第19届亚运会的吉祥物“琮琮”,代表的是世界遗产良渚古城遗址,名字来源于文物玉琮.琮琮全身以黄色调为主,头部刻有“饕餮纹”,展示给人们一种不屈不挠、坚强刚毅的精神.文旅部门将选定的“琮琮”形象图通过放大或缩小放置于不同的宣传版面上,这体现了数学中的( )
A.图形的平移 B.图形的轴对称
C.图形的相似 D.图形的旋转
【考点】相似图形.
【专题】图形的相似;应用意识.
【答案】C
【分析】根据把图形进行放大或缩小可判断出是图形的相似即可.
【解答】解:将选定的“琮琮”形象图通过放大或缩小放置于不同的宣传版面上,这体现了数学中的图形的相似.
故选:C.
【点评】本题主要考查图形的相似,解题的关键是理解题意.
二.填空题(共5小题)
6.(2024秋 西安期中)如图,五边形ABCDE∽五边形A'B'C'D'E',它们的相似比为3:4.已知BC=4.8cm,则B'C'= 6.4 cm.
【考点】相似多边形的性质.
【专题】图形的相似;推理能力.
【答案】6.4.
【分析】根据相似多边形的性质解答即可.
【解答】解:∵五边形ABCDE∽五边形A'B'C'D'E',它们的相似比为3:4,BC=4.8cm,
∴,
解得B′C′6.4.
故答案为:6.4.
【点评】本题考查的是相似多边形的性质,熟知相似多边形对应边的比相等是解题的关键.
7.(2024秋 宜兴市期中)两个相似多边形的相似比为1:4,则它们的面积的比为 1:16 .
【考点】相似多边形的性质.
【专题】图形的相似;推理能力.
【答案】1:16.
【分析】根据相似多边形的面积比等于相似比的平方计算即可.
【解答】解:∵两个相似多边形的相似比为1:4,
∴它们的面积的比为:()2=1:16,
故答案为:1:16.
【点评】本题考查的是相似多边形的性质,熟记相似多边形的面积比等于相似比的平方是解题的关键.
8.(2024秋 乐清市校级期中)两个相似五边形,一组对应边的长分别为2cm和3cm,若它们的面积之和为65cm2,则较小五边形的面积是 20cm2 .
【考点】相似多边形的性质.
【专题】图形的相似;推理能力.
【答案】20cm2.
【分析】根据相似多边形相似比即对应边的比,面积的比等于相似比的平方,即可解决.
【解答】解:设较小五边形与较大五边形的面积分别是x cm2,y cm2.
则,因而xy.
根据面积之和是65cm2,得到y+y=65,
解得:y=45,
则x45=20.
即较小五边形的面积分别是20cm2.
故答案为:20cm2.
【点评】本题考查相似多边形的性质.掌握相似多边形面积之比等于相似比的平方是解题的关键.
9.(2024秋 新城区期中)五边形ABCDE∽五边形A′B′C′D′E′,且它们的相似比为1:3.若五边形ABCDE的面积为6,则五边形A′B′C′D′E′的面积为 54 .
【考点】相似多边形的性质.
【专题】图形的相似;推理能力.
【答案】54.
【分析】根据相似多边形面积的比等于相似比的平方解答即可.
【解答】解:∵五边形ABCDE∽五边形A′B′C′D′E′,
∴五边形ABCDE与五边形A′B′C′D′E′的面积比等于相似比的平方.
∵相似比为1:3.五边形ABCDE的面积为6,
∴五边形A′B′C′D′E′的面积54,
故答案为:54.
【点评】本题考查了相似多边形的性质,解决本题的关键是掌握相似多边形面积的比等于相似比的平方.
10.(2024秋 郏县期末)书画经装裱后更便于收藏.如图,ABCD为长90cm、宽30cm的矩形,装裱后整幅画为矩形A'B'C'D',两矩形的对应边互相平行,且AB与A'B'的距离、CD与C′D′的距离都等于4cm.当AD与A'D'的距离、BC与B′C′距离都等于a cm,且矩形ABCD∽矩形A'B'C'D',整幅书画最美观此时,a的值为 12 .
【考点】相似多边形的性质;矩形的判定与性质.
【专题】图形的相似;运算能力.
【答案】12.
【分析】根据相似多边形的性质即可解答.
【解答】解:由题意AD=30cm,AB=90cm,A'B'=(90+2a)cm,A'D'=30+8=38cm,
∵矩形ABCD∽矩形A'B'C'D',
∴,
∴,
解得a=12,
故答案为:12.
【点评】本题考查相似多边形的性质,矩形的性质等知识,解题的关键是学会利用参数构建方程解决问题.
三.解答题(共5小题)
11.(2024秋 驿城区期中)如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,相似比是:2,连接EB,GD.
(1)求证:EB=GD;
(2)若∠DAB=60°,AB=2,求GD的长.
【考点】相似多边形的性质;全等三角形的判定与性质;等边三角形的判定与性质;菱形的性质.
【专题】图形的全等;等腰三角形与直角三角形;矩形 菱形 正方形;图形的相似;推理能力.
【答案】(1)证明过程见解答;
(2)GD.
【分析】(1)利用相似多边形的对应角相等和菱形的四边相等证得三角形全等后即可证得两条线段相等;
(2)连接BD交AC于点P,则BP⊥AC,根据∠DAB=60°得到BP=1,然后求得EP的长,最后利用勾股定理求得EB的长即可求得线段GD的长即可.
【解答】(1)证明:∵菱形AEFG∽菱形ABCD,∴∠EAG=∠BAD,
∴∠EAG+∠GAB=∠BAD+∠GAB,
∴∠EAB=∠GAD,
∵AE=AG,AB=AD,
∴△AEB≌△AGD,
∴EB=GD;
(2)连接BD交AC于点P,则BP⊥AC,
∵∠DAB=60°,
∴∠PAB=30°,
∵菱形AEFG∽菱形ABCD,相似比是:2,AB=2,
∴AE,BPAB=1,
∴AP,
∴EP,
∴EB,
∴GD.
【点评】本题主要考查相似多边形形的性质与判定,全等三角形的判定与性质,勾股定理,等边三角形的性质与判定,菱形的性质等知识的综合运用.
12.(2024秋 绥德县期中)如图,四边形ABCD∽四边形EFGH.
(1)求∠H的度数;
(2)若,CD=15,求HG的长.
【考点】相似多边形的性质.
【专题】图形的相似;推理能力.
【答案】12.
【分析】(1)根据四边形内角和是360°求出∠D,再根据相似多边形的对应角相等解答即可;
(2)根据相似多边形对边的比相等列出比例式,把已知数据代入计算即可.
【解答】解:(1)在四边形ABCD中,∠A=72°,∠B=135°,∠C=95°,
则∠D=360°﹣72°﹣135°﹣95°=58°,
∵四边形ABCD∽四边形EFGH,
∴∠H=∠D=58°;
(2)∵四边形ABCD∽四边形EFGH,
∴,即,
解得:HG=12.
【点评】本题考查的是相似多边形的性质,熟记相似多边形的对应角相等、对边的比相等是解题的关键.
13.(2024秋 萍乡期末)已知矩形ABCD中,AB=2,在BC中取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,求AD的长.
【考点】相似多边形的性质;矩形的性质;翻折变换(折叠问题).
【专题】图形的相似;运算能力.
【答案】.
【分析】可设AD=x,由四边形EFDC与矩形ABCD相似,根据相似多边形对应边的比相等列出比例式求解即可.
【解答】解:根据已知得四边形ABEF是正方形.
设AD=x,则FD=x﹣2,FE=2,
∵四边形EFDC与矩形ABCD相似,
∴,∴,
解得,(不合题意,舍去).
经检验:是分式方程的解,且符合题意.
∴,
即.
【点评】本题考查了翻折变换,相似多边形的性质,本题的关键是根据四边形EFDC与矩形ABCD相似得到比例式.
14.(2024秋 安庆期中)如图,一般书本的纸张是在原纸张多次对开的基础上得到的.矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,以此类推,如果各种开本的矩形都相似,那么AB与AD的比值是多少?
【考点】相似多边形的性质;矩形的性质;比例线段.
【专题】图形的相似;推理能力.
【答案】.
【分析】根据矩形ABCD的面积是矩形ABFE面积的2倍,得出相似图形面积比是相似比的平方,进而得出的值.
【解答】解:∵矩形ABCD的面积是矩形ABFE面积的2倍,
∵各种开本的矩形都相似,
∴,
∴.
答:AB与AD的比值是.
【点评】此题主要考查了多边形的相似的性质,得出相似图形面积比是相似比的平方是解决问题的关键.
15.(2024秋 肇源县期末)按2:1的比画出长方形放大后的图形,再按1:3的比画出三角形缩小后的图形.
【考点】相似多边形的性质.
【专题】图形的相似;几何直观.
【答案】图形见解答.
【分析】根据相似多边形的性质,即可解答.
【解答】解:如图:
∴长方形ABCD,△EFG即为所求.
【点评】本题考查了相似多边形的性质,熟练掌握相似多边形的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.夯实基础 相似多边形
一.选择题(共5小题)
1.(2024秋 雁塔区校级期中)如图1是古希腊时期的巴台农神庙,把图1中用虚线表示的矩形画成图2矩形ABCD,当以矩形ABCD的宽AB为边作正方形ABEF时,惊奇地发现矩形CDFE与矩形ABCD相似,则等于( )
A. B. C. D.
2.(2024秋 松江区期中)下列图形一定是相似图形的是( )
A.两个等腰三角形
B.两个面积相等的三角形
C.两个正方形
D.两个菱形
3.(2024秋 崂山区期中)某学校致力于劳动教育的探索与实践,在校内设立了“田园风光”和“耘梦园”两个相似的矩形劳动场所,它们的相似比是1:2.若两个劳动场所种植相同品种的蔬菜,在每平方米所需农资成本(主要包括化肥、农药以及灌溉用水)不变的情况下,“田园风光”的农资成本为200元,则“耘梦园”的农资成本为( )
A.800元 B.400元 C.100元 D.50元
4.(2024 连云港)下列网格中各个小正方形的边长均为1,阴影部分图形分别记作甲、乙、丙、丁,其中是相似形的为( )
A.甲和乙 B.乙和丁 C.甲和丙 D.甲和丁
5.(2024秋 阳谷县期末)如图是杭州第19届亚运会的吉祥物“琮琮”,代表的是世界遗产良渚古城遗址,名字来源于文物玉琮.琮琮全身以黄色调为主,头部刻有“饕餮纹”,展示给人们一种不屈不挠、坚强刚毅的精神.文旅部门将选定的“琮琮”形象图通过放大或缩小放置于不同的宣传版面上,这体现了数学中的( )
A.图形的平移 B.图形的轴对称
C.图形的相似 D.图形的旋转
二.填空题(共5小题)
6.(2024秋 西安期中)如图,五边形ABCDE∽五边形A'B'C'D'E',它们的相似比为3:4.已知BC=4.8cm,则B'C'= cm.
7.(2024秋 宜兴市期中)两个相似多边形的相似比为1:4,则它们的面积的比为 .
8.(2024秋 乐清市校级期中)两个相似五边形,一组对应边的长分别为2cm和3cm,若它们的面积之和为65cm2,则较小五边形的面积是 .
9.(2024秋 新城区期中)五边形ABCDE∽五边形A′B′C′D′E′,且它们的相似比为1:3.若五边形ABCDE的面积为6,则五边形A′B′C′D′E′的面积为 .
10.(2024秋 郏县期末)书画经装裱后更便于收藏.如图,ABCD为长90cm、宽30cm的矩形,装裱后整幅画为矩形A'B'C'D',两矩形的对应边互相平行,且AB与A'B'的距离、CD与C′D′的距离都等于4cm.当AD与A'D'的距离、BC与B′C′距离都等于a cm,且矩形ABCD∽矩形A'B'C'D',整幅书画最美观此时,a的值为 .
三.解答题(共5小题)
11.(2024秋 驿城区期中)如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,相似比是:2,连接EB,GD.
(1)求证:EB=GD;
(2)若∠DAB=60°,AB=2,求GD的长.
12.(2024秋 绥德县期中)如图,四边形ABCD∽四边形EFGH.
(1)求∠H的度数;
(2)若,CD=15,求HG的长.
13.(2024秋 萍乡期末)已知矩形ABCD中,AB=2,在BC中取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,求AD的长.
14.(2024秋 安庆期中)如图,一般书本的纸张是在原纸张多次对开的基础上得到的.矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,以此类推,如果各种开本的矩形都相似,那么AB与AD的比值是多少?
15.(2024秋 肇源县期末)按2:1的比画出长方形放大后的图形,再按1:3的比画出三角形缩小后的图形.
预习衔接.夯实基础 相似多边形
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 雁塔区校级期中)如图1是古希腊时期的巴台农神庙,把图1中用虚线表示的矩形画成图2矩形ABCD,当以矩形ABCD的宽AB为边作正方形ABEF时,惊奇地发现矩形CDFE与矩形ABCD相似,则等于( )
A. B. C. D.
【考点】相似多边形的性质;矩形的性质;正方形的性质.
【专题】图形的相似;推理能力.
【答案】B
【分析】根据相似多边形的对应边的比相等列出算式,解方程得到答案.
【解答】解:设EC=a,BE=b,则BC=a+b,
∵矩形CDFE∽矩形DABC,
∴,即,
整理得:a2+ab﹣b2=0,
∴()21=0,
解得:(负值舍去),
故选:B.
【点评】本题考查的是相似多边形的性质、熟记相似多边形的对应边成比例是解题的关键.
2.(2024秋 松江区期中)下列图形一定是相似图形的是( )
A.两个等腰三角形
B.两个面积相等的三角形
C.两个正方形
D.两个菱形
【考点】相似图形.
【专题】图形的相似;推理能力.
【答案】C
【分析】根据相似三角形的判定方法进行判断.
【解答】解:A、两个等腰三角形不一定相似,不符合题意;
B、两个面积相等的三角形不一定相似,不符合题意;
C、两个正方形一定相似,符合题意;
D、两个菱形不一定相似,不符合题意.
故选:C.
【点评】本题考查了相似图形:把形状相同的图形称为相似图形.
3.(2024秋 崂山区期中)某学校致力于劳动教育的探索与实践,在校内设立了“田园风光”和“耘梦园”两个相似的矩形劳动场所,它们的相似比是1:2.若两个劳动场所种植相同品种的蔬菜,在每平方米所需农资成本(主要包括化肥、农药以及灌溉用水)不变的情况下,“田园风光”的农资成本为200元,则“耘梦园”的农资成本为( )
A.800元 B.400元 C.100元 D.50元
【考点】相似多边形的性质.
【专题】图形的相似;应用意识.
【答案】A
【分析】根据相似多边形的性质求出“田园风光”和“耘梦园”两个相似的矩形劳动场所的面积比,再计算农资成本即可.
【解答】解:∵“田园风光”和“耘梦园”两个相似的矩形劳动场所,它们的相似比是1:2,
∴“田园风光”和“耘梦园”两个相似的矩形劳动场所的面积比为1:4,
∵“田园风光”的农资成本为200元,
∴“耘梦园”的农资成本为:200×4=800(元).
故选:A.
【点评】本题考查了相似多边形的性质,解题的关键是掌握相似多边形的面积比等于相似比的平方.
4.(2024 连云港)下列网格中各个小正方形的边长均为1,阴影部分图形分别记作甲、乙、丙、丁,其中是相似形的为( )
A.甲和乙 B.乙和丁 C.甲和丙 D.甲和丁
【考点】相似图形.
【专题】图形的相似;推理能力.
【答案】D
【分析】如果两个多边形的对应角相等,对应边的比相等,则这两个多边形是相似多边形.
【解答】解:观察可得:甲和丁对应角相等,对应边成比例,且形状相同,大小不同,
故选:D.
【点评】本题主要考查了相似多边形的性质,相似多边形的性质为:①对应角相等;②对应边的比相等.
5.(2024秋 阳谷县期末)如图是杭州第19届亚运会的吉祥物“琮琮”,代表的是世界遗产良渚古城遗址,名字来源于文物玉琮.琮琮全身以黄色调为主,头部刻有“饕餮纹”,展示给人们一种不屈不挠、坚强刚毅的精神.文旅部门将选定的“琮琮”形象图通过放大或缩小放置于不同的宣传版面上,这体现了数学中的( )
A.图形的平移 B.图形的轴对称
C.图形的相似 D.图形的旋转
【考点】相似图形.
【专题】图形的相似;应用意识.
【答案】C
【分析】根据把图形进行放大或缩小可判断出是图形的相似即可.
【解答】解:将选定的“琮琮”形象图通过放大或缩小放置于不同的宣传版面上,这体现了数学中的图形的相似.
故选:C.
【点评】本题主要考查图形的相似,解题的关键是理解题意.
二.填空题(共5小题)
6.(2024秋 西安期中)如图,五边形ABCDE∽五边形A'B'C'D'E',它们的相似比为3:4.已知BC=4.8cm,则B'C'= 6.4 cm.
【考点】相似多边形的性质.
【专题】图形的相似;推理能力.
【答案】6.4.
【分析】根据相似多边形的性质解答即可.
【解答】解:∵五边形ABCDE∽五边形A'B'C'D'E',它们的相似比为3:4,BC=4.8cm,
∴,
解得B′C′6.4.
故答案为:6.4.
【点评】本题考查的是相似多边形的性质,熟知相似多边形对应边的比相等是解题的关键.
7.(2024秋 宜兴市期中)两个相似多边形的相似比为1:4,则它们的面积的比为 1:16 .
【考点】相似多边形的性质.
【专题】图形的相似;推理能力.
【答案】1:16.
【分析】根据相似多边形的面积比等于相似比的平方计算即可.
【解答】解:∵两个相似多边形的相似比为1:4,
∴它们的面积的比为:()2=1:16,
故答案为:1:16.
【点评】本题考查的是相似多边形的性质,熟记相似多边形的面积比等于相似比的平方是解题的关键.
8.(2024秋 乐清市校级期中)两个相似五边形,一组对应边的长分别为2cm和3cm,若它们的面积之和为65cm2,则较小五边形的面积是 20cm2 .
【考点】相似多边形的性质.
【专题】图形的相似;推理能力.
【答案】20cm2.
【分析】根据相似多边形相似比即对应边的比,面积的比等于相似比的平方,即可解决.
【解答】解:设较小五边形与较大五边形的面积分别是x cm2,y cm2.
则,因而xy.
根据面积之和是65cm2,得到y+y=65,
解得:y=45,
则x45=20.
即较小五边形的面积分别是20cm2.
故答案为:20cm2.
【点评】本题考查相似多边形的性质.掌握相似多边形面积之比等于相似比的平方是解题的关键.
9.(2024秋 新城区期中)五边形ABCDE∽五边形A′B′C′D′E′,且它们的相似比为1:3.若五边形ABCDE的面积为6,则五边形A′B′C′D′E′的面积为 54 .
【考点】相似多边形的性质.
【专题】图形的相似;推理能力.
【答案】54.
【分析】根据相似多边形面积的比等于相似比的平方解答即可.
【解答】解:∵五边形ABCDE∽五边形A′B′C′D′E′,
∴五边形ABCDE与五边形A′B′C′D′E′的面积比等于相似比的平方.
∵相似比为1:3.五边形ABCDE的面积为6,
∴五边形A′B′C′D′E′的面积54,
故答案为:54.
【点评】本题考查了相似多边形的性质,解决本题的关键是掌握相似多边形面积的比等于相似比的平方.
10.(2024秋 郏县期末)书画经装裱后更便于收藏.如图,ABCD为长90cm、宽30cm的矩形,装裱后整幅画为矩形A'B'C'D',两矩形的对应边互相平行,且AB与A'B'的距离、CD与C′D′的距离都等于4cm.当AD与A'D'的距离、BC与B′C′距离都等于a cm,且矩形ABCD∽矩形A'B'C'D',整幅书画最美观此时,a的值为 12 .
【考点】相似多边形的性质;矩形的判定与性质.
【专题】图形的相似;运算能力.
【答案】12.
【分析】根据相似多边形的性质即可解答.
【解答】解:由题意AD=30cm,AB=90cm,A'B'=(90+2a)cm,A'D'=30+8=38cm,
∵矩形ABCD∽矩形A'B'C'D',
∴,
∴,
解得a=12,
故答案为:12.
【点评】本题考查相似多边形的性质,矩形的性质等知识,解题的关键是学会利用参数构建方程解决问题.
三.解答题(共5小题)
11.(2024秋 驿城区期中)如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,相似比是:2,连接EB,GD.
(1)求证:EB=GD;
(2)若∠DAB=60°,AB=2,求GD的长.
【考点】相似多边形的性质;全等三角形的判定与性质;等边三角形的判定与性质;菱形的性质.
【专题】图形的全等;等腰三角形与直角三角形;矩形 菱形 正方形;图形的相似;推理能力.
【答案】(1)证明过程见解答;
(2)GD.
【分析】(1)利用相似多边形的对应角相等和菱形的四边相等证得三角形全等后即可证得两条线段相等;
(2)连接BD交AC于点P,则BP⊥AC,根据∠DAB=60°得到BP=1,然后求得EP的长,最后利用勾股定理求得EB的长即可求得线段GD的长即可.
【解答】(1)证明:∵菱形AEFG∽菱形ABCD,∴∠EAG=∠BAD,
∴∠EAG+∠GAB=∠BAD+∠GAB,
∴∠EAB=∠GAD,
∵AE=AG,AB=AD,
∴△AEB≌△AGD,
∴EB=GD;
(2)连接BD交AC于点P,则BP⊥AC,
∵∠DAB=60°,
∴∠PAB=30°,
∵菱形AEFG∽菱形ABCD,相似比是:2,AB=2,
∴AE,BPAB=1,
∴AP,
∴EP,
∴EB,
∴GD.
【点评】本题主要考查相似多边形形的性质与判定,全等三角形的判定与性质,勾股定理,等边三角形的性质与判定,菱形的性质等知识的综合运用.
12.(2024秋 绥德县期中)如图,四边形ABCD∽四边形EFGH.
(1)求∠H的度数;
(2)若,CD=15,求HG的长.
【考点】相似多边形的性质.
【专题】图形的相似;推理能力.
【答案】12.
【分析】(1)根据四边形内角和是360°求出∠D,再根据相似多边形的对应角相等解答即可;
(2)根据相似多边形对边的比相等列出比例式,把已知数据代入计算即可.
【解答】解:(1)在四边形ABCD中,∠A=72°,∠B=135°,∠C=95°,
则∠D=360°﹣72°﹣135°﹣95°=58°,
∵四边形ABCD∽四边形EFGH,
∴∠H=∠D=58°;
(2)∵四边形ABCD∽四边形EFGH,
∴,即,
解得:HG=12.
【点评】本题考查的是相似多边形的性质,熟记相似多边形的对应角相等、对边的比相等是解题的关键.
13.(2024秋 萍乡期末)已知矩形ABCD中,AB=2,在BC中取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,求AD的长.
【考点】相似多边形的性质;矩形的性质;翻折变换(折叠问题).
【专题】图形的相似;运算能力.
【答案】.
【分析】可设AD=x,由四边形EFDC与矩形ABCD相似,根据相似多边形对应边的比相等列出比例式求解即可.
【解答】解:根据已知得四边形ABEF是正方形.
设AD=x,则FD=x﹣2,FE=2,
∵四边形EFDC与矩形ABCD相似,
∴,∴,
解得,(不合题意,舍去).
经检验:是分式方程的解,且符合题意.
∴,
即.
【点评】本题考查了翻折变换,相似多边形的性质,本题的关键是根据四边形EFDC与矩形ABCD相似得到比例式.
14.(2024秋 安庆期中)如图,一般书本的纸张是在原纸张多次对开的基础上得到的.矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,以此类推,如果各种开本的矩形都相似,那么AB与AD的比值是多少?
【考点】相似多边形的性质;矩形的性质;比例线段.
【专题】图形的相似;推理能力.
【答案】.
【分析】根据矩形ABCD的面积是矩形ABFE面积的2倍,得出相似图形面积比是相似比的平方,进而得出的值.
【解答】解:∵矩形ABCD的面积是矩形ABFE面积的2倍,
∵各种开本的矩形都相似,
∴,
∴.
答:AB与AD的比值是.
【点评】此题主要考查了多边形的相似的性质,得出相似图形面积比是相似比的平方是解决问题的关键.
15.(2024秋 肇源县期末)按2:1的比画出长方形放大后的图形,再按1:3的比画出三角形缩小后的图形.
【考点】相似多边形的性质.
【专题】图形的相似;几何直观.
【答案】图形见解答.
【分析】根据相似多边形的性质,即可解答.
【解答】解:如图:
∴长方形ABCD,△EFG即为所求.
【点评】本题考查了相似多边形的性质,熟练掌握相似多边形的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
