4.7相似三角形的性质(预习衔接.夯实基础.含解析)-2025-2026学年九年级上册数学北师大版
文档属性
| 名称 | 4.7相似三角形的性质(预习衔接.夯实基础.含解析)-2025-2026学年九年级上册数学北师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 212.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 21:06:01 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
预习衔接.夯实基础 相似三角形的性质
一.选择题(共5小题)
1.(2024秋 龙岗区期中)如图,带有刻度的直尺结合数轴作图,已知图中过点B和8的两条线段(两条线段的另一端在刻度尺上分别对应3和5)相互平行.若点A在数轴上表示的数是﹣2且点A与刻度尺上的0刻度重合,则AB的长度是( )
A.3 B.4 C.5 D.6
2.(2024秋 泉州期中)若两个相似三角形周长的比为2:3,则这两个三角形的面积比是( )
A.1:2 B.2:3 C.4:6 D.4:9
3.(2024秋 杨浦区期中)已知△ABC的三边都不相等,如果△ABC与△DEF相似,且∠B=∠D,那么下列等式一定不成立的是( )
A. B. C. D.
4.(2024 通海县模拟)如图,△OAB∽△OCD,OA:OC=3:2,△OAB与△OCD的面积分别是S1与S2,周长分别是C1与C2,则下列说法正确的是( )
A. B. C. D.
5.(2024 白银模拟)△ABC∽△A′B′C′,已知AB=5,A′B′=6,△ABC面积为10,那么另一个三角形的面积为( )
A.15 B.14.4 C.12 D.10.8
二.填空题(共5小题)
6.(2024秋 中原区校级期中)已知,在平面直角坐标系xOy中,直线y=2x+4与x轴、y轴相交于A、B两点,且点C的坐标为(6,4),连接AC,与y轴相交于点D,点E在x轴上,如果△ABD和△ACE相似,则点E的坐标为 .
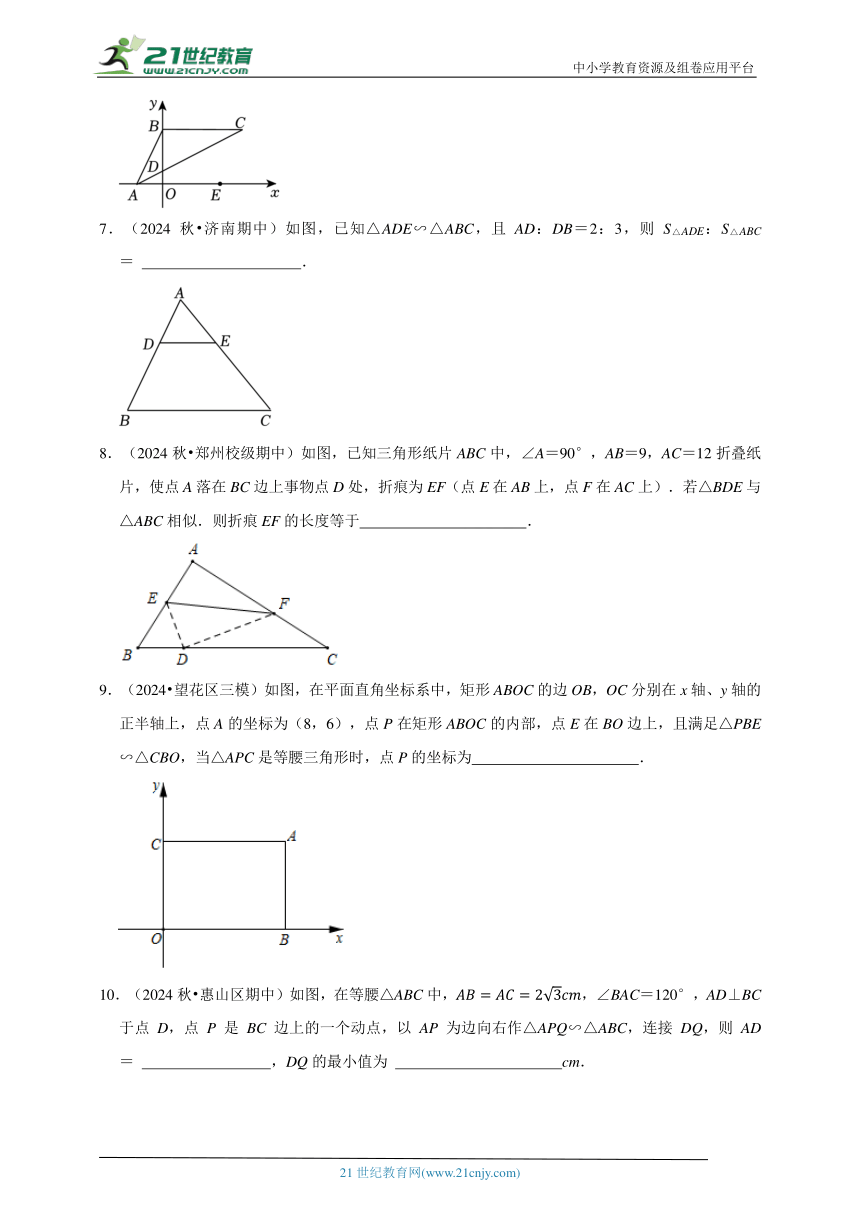
7.(2024秋 济南期中)如图,已知△ADE∽△ABC,且AD:DB=2:3,则S△ADE:S△ABC= .
8.(2024秋 郑州校级期中)如图,已知三角形纸片ABC中,∠A=90°,AB=9,AC=12折叠纸片,使点A落在BC边上事物点D处,折痕为EF(点E在AB上,点F在AC上).若△BDE与△ABC相似.则折痕EF的长度等于 .
9.(2024 望花区三模)如图,在平面直角坐标系中,矩形ABOC的边OB,OC分别在x轴、y轴的正半轴上,点A的坐标为(8,6),点P在矩形ABOC的内部,点E在BO边上,且满足△PBE∽△CBO,当△APC是等腰三角形时,点P的坐标为 .
10.(2024秋 惠山区期中)如图,在等腰△ABC中,,∠BAC=120°,AD⊥BC于点D,点P是BC边上的一个动点,以AP为边向右作△APQ∽△ABC,连接DQ,则AD= ,DQ的最小值为 cm.
三.解答题(共5小题)
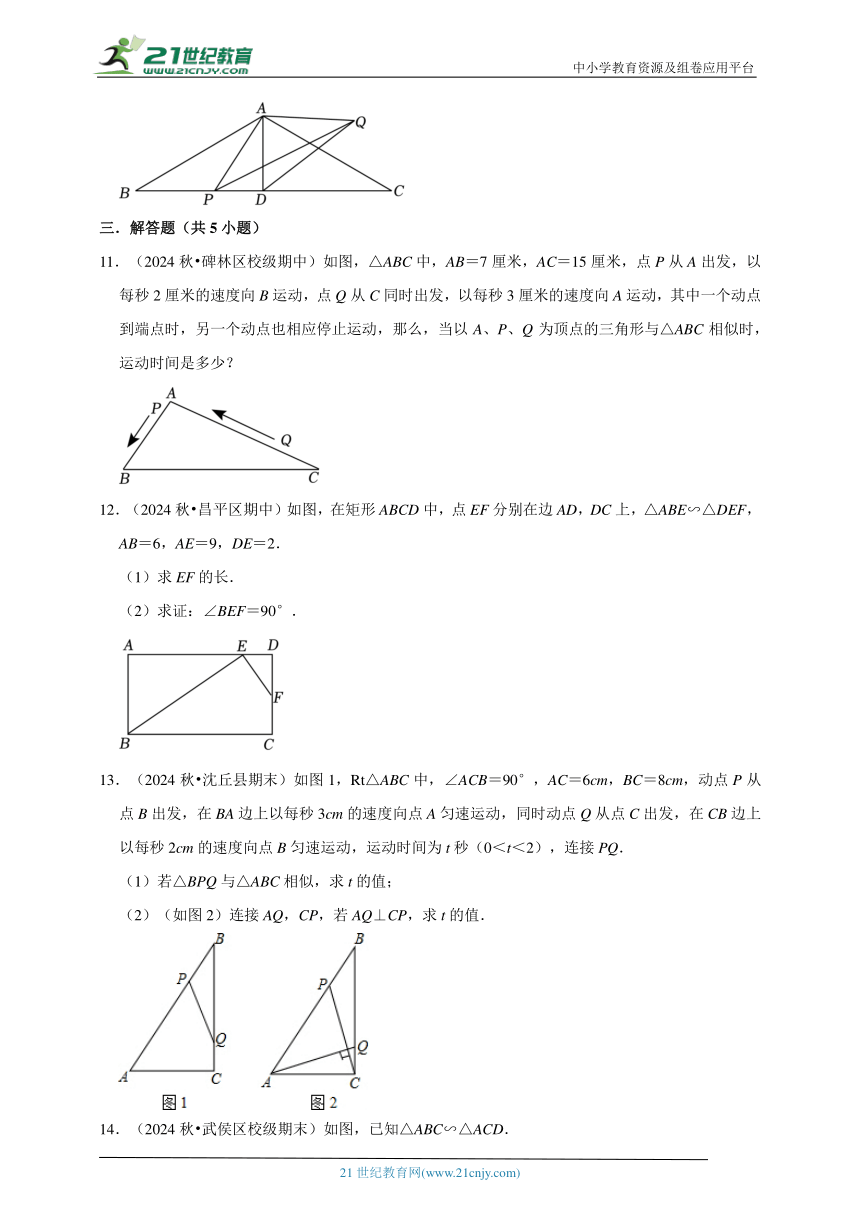
11.(2024秋 碑林区校级期中)如图,△ABC中,AB=7厘米,AC=15厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?
12.(2024秋 昌平区期中)如图,在矩形ABCD中,点EF分别在边AD,DC上,△ABE∽△DEF,AB=6,AE=9,DE=2.
(1)求EF的长.
(2)求证:∠BEF=90°.
13.(2024秋 沈丘县期末)如图1,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒3cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒2cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)(如图2)连接AQ,CP,若AQ⊥CP,求t的值.
14.(2024秋 武侯区校级期末)如图,已知△ABC∽△ACD.
(1)若CD平分∠ACB,∠ACD=35°,求∠ADC的度数;
(2)若AD=3,BD=5,求AC的长.
15.(2024秋 新民市期中)四边形的一条对角线把这个四边形分成两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线称为这个四边形的“理想对角线”.
(1)如图1,在四边形ABCD中,∠ABC=70°,AB=AD,AD∥BC,当∠ADC=145°时.求证:对角线BD是四边形ABCD的“理想对角线”.
(2)如图2,四边形ABCD中,AC平分∠BCD,当∠BCD与∠BAD满足什么关系时,对角线AC是四边形ABCD的“理想对角线”,请说明理由.
预习衔接.夯实基础 相似三角形的性质
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 龙岗区期中)如图,带有刻度的直尺结合数轴作图,已知图中过点B和8的两条线段(两条线段的另一端在刻度尺上分别对应3和5)相互平行.若点A在数轴上表示的数是﹣2且点A与刻度尺上的0刻度重合,则AB的长度是( )
A.3 B.4 C.5 D.6
【考点】相似三角形的性质;数轴.
【专题】计算题;数形结合;运算能力.
【答案】D
【分析】利用数轴知识和三角形相似的性质解答.
【解答】解:∵由题意可知线段平行,
∴可以找到相似三角形,通过三角形相似可以得到相似比的等式,
,
,
AB=6.
故选:D.
【点评】本题考查了数轴和三角形相似的性质,解题的关键是掌握数轴知识和三角形相似的性质.
2.(2024秋 泉州期中)若两个相似三角形周长的比为2:3,则这两个三角形的面积比是( )
A.1:2 B.2:3 C.4:6 D.4:9
【考点】相似三角形的性质.
【专题】图形的相似;推理能力.
【答案】D
【分析】相似三角形周长的比等于相似比,相似三角形面积的比等于相似比的平方,由此即可计算.
【解答】解:∵两个相似三角形的周长比为2:3,
∴两个相似三角形的相似比为2:3,
∴这两个相似三角形的面积比为22:32=4:9.
故选:D.
【点评】本题主要考查相似三角形的性质,关键是掌握相似三角形的性质:相似三角形面积的比等于相似比的平方.
3.(2024秋 杨浦区期中)已知△ABC的三边都不相等,如果△ABC与△DEF相似,且∠B=∠D,那么下列等式一定不成立的是( )
A. B. C. D.
【考点】相似三角形的性质.
【专题】图形的相似;推理能力.
【答案】C
【分析】根据相似三角形的性质解答即可.
【解答】解:∵△ABC与△DEF相似,且∠B=∠D,
∴△ABC∽△EDF或△ABC∽△FDE,
当△ABC∽△EDF时,
,,故A、D正确,不符合题意;
当△ABC∽△FDE时,
,故B正确,不符合题意;
两组相似三角形中BC,EF均不是对应边,故C一定不成立.
故选:C.
【点评】本题考查的是相似三角形的性质,熟知相似三角形的对应边成比例,对应角相等是解题的关键.
4.(2024 通海县模拟)如图,△OAB∽△OCD,OA:OC=3:2,△OAB与△OCD的面积分别是S1与S2,周长分别是C1与C2,则下列说法正确的是( )
A. B. C. D.
【考点】相似三角形的性质.
【专题】图形的相似;几何直观.
【答案】A
【分析】根据相似三角形的性质判断即可.
【解答】解:∵△OAB∽△OCD,OA:OC=3:2,
∴,A正确;
∴,B错误;
∴,C错误;
∴OA:OC=3:2,D错误;
故选:A.
【点评】本题考查了相似三角形的性质,熟练掌握相似三角形的性质定理是解题的关键.
5.(2024 白银模拟)△ABC∽△A′B′C′,已知AB=5,A′B′=6,△ABC面积为10,那么另一个三角形的面积为( )
A.15 B.14.4 C.12 D.10.8
【考点】相似三角形的性质.
【答案】B
【分析】利用相似三角形的性质得出两三角形的面积比,进而求出即可.
【解答】解:∵△ABC∽△A′B′C′,AB=5,A′B′=6,
∴,
∵△ABC面积为10,
∴解得:S△A′B′C′=14.4.
故选:B.
【点评】此题主要考查了相似三角形的性质,利用相似比与面积比的关系得出是解题关键.
二.填空题(共5小题)
6.(2024秋 中原区校级期中)已知,在平面直角坐标系xOy中,直线y=2x+4与x轴、y轴相交于A、B两点,且点C的坐标为(6,4),连接AC,与y轴相交于点D,点E在x轴上,如果△ABD和△ACE相似,则点E的坐标为 (4,0)或(,0) .
【考点】相似三角形的性质;一次函数的性质;一次函数图象上点的坐标特征.
【专题】图形的相似;推理能力.
【答案】(4,0)或(,0).
【分析】首先根据一次函数确定点A(﹣2,0),B(0,4),然后根据点C判定BC∥x轴,进而得出∠C=∠CAE,然后根据相似三角形的判定方法列比例式解答即可.
【解答】解:当x=0时,则y=2x+4=4,
当y=0时,则2x+4=0,解得x=﹣2;
∴A点的坐标为(﹣2,0),B点的坐标为(0,4),
∵C(6,4),
∴BC∥x轴,BC=6,AC4,
∴∠C=∠CAE,
如果△ABD和△ACE相似,
则或,
即或,
解得AE=6或AE,
∴OE=4或OE,
∴点E的坐标为:(4,0)或(,0).
【点评】本题考查了坐标与图形,相似三角形的判定与性质,掌握相似三角形判定方法是解题的关键.
7.(2024秋 济南期中)如图,已知△ADE∽△ABC,且AD:DB=2:3,则S△ADE:S△ABC= .
【考点】相似三角形的性质.
【专题】图形的相似;推理能力.
【答案】.
【分析】先根据题意得出相似三角形的相似比,进而可得出结论.
【解答】解:∵△ADE∽△ABC,且AD:DB=2:3,
∴,
∴()2,
故答案为:.
【点评】本题考查的是相似三角形的性质,熟知相似三角形面积的比等于相似比的平方是解题的关键.
8.(2024秋 郑州校级期中)如图,已知三角形纸片ABC中,∠A=90°,AB=9,AC=12折叠纸片,使点A落在BC边上事物点D处,折痕为EF(点E在AB上,点F在AC上).若△BDE与△ABC相似.则折痕EF的长度等于 或4 .
【考点】相似三角形的性质;翻折变换(折叠问题).
【专题】图形的相似;推理能力.
【答案】见试题解答内容
【分析】若△BDE与△ABC相似,则∠BED=90°或∠BDE=90°,
①当∠BED=90°时,根据相似三角形的性质即可得到结论;②当∠BDE=90°时,由折叠的性质得,∠EDF=∠A=90°,则点F在BC上,这与题意不符.
【解答】解:若△BDE与△ABC相似,则∠BED=90°或∠BDE=90°,
①当∠BED=90°时,∵∠A=90°,
∴DE∥AC,
∴,
由折叠的性质得,DE=AE,∠AEF=∠DEF,
∴,
解得:AE,
∵DE∥AC,
∴∠AFE=∠DEF,
∴∠AEF=∠AFE,
∴△AEF是等腰直角三角形,
∴EFAE;
②当∠BDE=90°时,
由折叠的性质得,∠EDF=∠A=90°,
则点F与点C重合,
∵∠A=90°,AB=9,AC=12,
∴BC15,
∵∠A=∠EDB=90°,∠B=∠B,
∴△BDE∽△BAC,
∴,
∴,
∴DE=4,
∴AE=4,
∴EF4,
综上所述,折痕EF的长度等于或4,
故答案为:或4.
【点评】本题考查了相似三角形的性质,等腰直角三角形的判断和现在,折叠的性质,正确的理解题意是解题的关键.
9.(2024 望花区三模)如图,在平面直角坐标系中,矩形ABOC的边OB,OC分别在x轴、y轴的正半轴上,点A的坐标为(8,6),点P在矩形ABOC的内部,点E在BO边上,且满足△PBE∽△CBO,当△APC是等腰三角形时,点P的坐标为 (,)或(4,3) .
【考点】相似三角形的性质;坐标与图形性质;等腰三角形的性质;矩形的性质.
【专题】矩形 菱形 正方形;图形的相似;推理能力.
【答案】(,)或(4,3).
【分析】由题意得出P点在AC的垂直平分线上或在以点C为圆心AC为半径的圆弧上,由此分两种情形分别求解,可得结论.
【解答】解:∵点P在矩形ABOC的内部,且△APC是等腰三角形,
∴P点在AC的垂直平分线上或在以点C为圆心AC为半径的圆弧上;
①当P点在AC的垂直平分线上时,点P同时在BC上,AC的垂直平分线与BO的交点即是E,如图1所示:
∵PE⊥BO,CO⊥BO,
∴PE∥CO,
∴△PBE∽△CBO,
∵四边形ABOC是矩形,A点的坐标为(8,6),
∴点P横坐标为4,OC=6,BO=8,BE=4,
∵△PBE∽△CBO,
∴,即,
解得:PE=3,
∴点P(4,3);
②P点在以点C为圆心AC为半径的圆弧上,圆弧与BC的交点为P,
过点P作PE⊥BO于E,如图2所示:
∵CO⊥BO,
∴PE∥CO,
∴△PBE∽△CBO,
∵四边形ABOC是矩形,A点的坐标为(8,6),
∴AC=BO=8,CP=8,AB=OC=6,
∴BC10,
∴BP=2,
∵△PBE∽△CBO,
∴,即:,
解得:PE,BE,
∴OE=8,
∴点P(,);
综上所述:点P的坐标为:(,)或(4,3);
故答案为:(,)或(4,3).
【点评】本题考查了相似三角形的判定与性质、矩形的性质、等腰三角形的判定与性质、坐标与图形的性质、平行线的判定、勾股定理、分类讨论等知识,熟练掌握相似三角形与等腰三角形的判定与性质是解题的关键.
10.(2024秋 惠山区期中)如图,在等腰△ABC中,,∠BAC=120°,AD⊥BC于点D,点P是BC边上的一个动点,以AP为边向右作△APQ∽△ABC,连接DQ,则AD= ,DQ的最小值为 cm.
【考点】相似三角形的性质;等腰三角形的性质.
【专题】等腰三角形与直角三角形;运算能力.
【答案】,.
【分析】,先证△ABP≌△ACQ,易得∠DCQ恒为60°,根据题意易得AD的值,根据点到直线的所有连线中,垂线段最短,可知DQ的最小值即为DH,进行求解即可.
【解答】解:连接CQ,过点D作DH⊥CQ,垂足为H,如图所示:
∵△APQ∽△ABC,
∴∠PAQ=∠BAC,AP:AB=AQ:AC,
∴∠BAP=∠CAQ,
∵AB=AC,
∴AP=AQ,
在△ABP和△ACQ中,
,
∴△ABP≌△ACQ(SAS),
∴∠ACQ=∠ACB,
∵∠BAC=120°,
∴∠ABC=∠ACB=30°,
∴∠ACQ=30°,
∴∠DCQ=60°,
∴∠CDH=30°,
∵AB=ACcm,∠BAC=120°,
∴AC=6,AD,
∵AD⊥BC,
∴CD=3,
∴CH,DH.
∴DQ的最小值即为.
故答案为:,.
【点评】本题考查相似三角形和等腰三角形的性质,在运动过程中找出Q的运动轨迹,并运用垂线段最短求解是解决本题的关键.
三.解答题(共5小题)
11.(2024秋 碑林区校级期中)如图,△ABC中,AB=7厘米,AC=15厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?
【考点】相似三角形的性质.
【专题】图形的相似;运算能力;推理能力.
【答案】运动时间是秒.
【分析】首先设运动了t秒,根据题意得:AP=2tcm,CQ=3tcm,然后分别从当△APQ∽△ABC与当△APQ∽△ACB时去分析得出t的值,再由“其中一个动点到端点时,另一个动点也相应停止运动”可得t的取值范围,即可得出答案.
【解答】解:设运动了t秒.
根据题意得:AP=2t cm,CQ=3t cm,则AQ=AC﹣CQ=(15﹣3t)cm,
当△APQ∽△ABC时,,
即,
解得,
当△APQ∽△ACB时,,
即,
解得,
∵其中一个动点到端点时,另一个动点也相应停止运动,
∴P点运动时长最多为秒,Q点运动时长最多为15÷3=5秒,
∴,
∵,,
∴,
故当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是秒.
【点评】此题考查了相似三角形的性质.相似三角形的对应边的比相等.
12.(2024秋 昌平区期中)如图,在矩形ABCD中,点EF分别在边AD,DC上,△ABE∽△DEF,AB=6,AE=9,DE=2.
(1)求EF的长.
(2)求证:∠BEF=90°.
【考点】相似三角形的性质;勾股定理的逆定理;矩形的性质.
【专题】几何综合题;推理能力.
【答案】见试题解答内容
【分析】(1)根据两三角形相似,得到对应边成比例,,结合已知条件,从而得到DF的长,利用直角三角形勾股定理,从而得到结果;
(2)利用两三角形相似,得到对应角相等,结合直角三角形两锐角互余,从而证得结果.
【解答】(1)解:∵△ABE∽△DEF,
∴,
∵AB=6,AE=9,DE=2,
∴,
∴DF=3,
∵矩形ABCD,
∴∠EDF=90°,
∴在Rt△DEF中,
;
(2)证明:∵△ABE∽△DEF,
∴∠ABE=∠DEF,
∵在Rt△ABE中,∠ABE+∠AEB=90°,
∴∠DEF+∠AEB=90°,
∴∠BEF=90°.
【点评】本题考查了三角形相似的性质,以及矩形性质,勾股定理的应用,关键是合理应用三角形相似的性质.
13.(2024秋 沈丘县期末)如图1,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒3cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒2cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)(如图2)连接AQ,CP,若AQ⊥CP,求t的值.
【考点】相似三角形的性质.
【专题】图形的相似;推理能力.
【答案】见试题解答内容
【分析】(1)根据勾股定理求出AB,分△BPQ∽△BAC、△BPQ∽△BCA两种情况,根据相似三角形的性质列出比例式,计算即可;
(2)过P作PM⊥BC于点M,AQ,CP交于点N,则有PB=5t,PM=3t,BQ=8﹣4t,根据△ACQ∽△CMP,得出AC:CM=CQ:MP,代入计算即可.
【解答】解:(1)①当△BPQ∽△BAC时,
∵,BP=3t,QC=2t,AB=10cm,BC=8cm,
∴,
∴,
②当△BPQ∽△BCA时,
∵,
∴,
∴;
∴或时,△BPQ与△ABC相似;
(2)如图所示,过P作PM⊥BC于点M,AQ,CP交于点N,
则有PB=3t,,,,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM且∠ACQ=∠PMC=90°,
∴△ACQ∽△CMP,
∴,
∴
解得:.
【点评】此题是相似形综合题,主要考查了相似三角形的判定与性质,勾股定理,直角三角形的性质,等腰三角形的性质,由三角形相似得出对应边成比例是解题的关键.
14.(2024秋 武侯区校级期末)如图,已知△ABC∽△ACD.
(1)若CD平分∠ACB,∠ACD=35°,求∠ADC的度数;
(2)若AD=3,BD=5,求AC的长.
【考点】相似三角形的性质.
【专题】图形的相似;推理能力.
【答案】(1)70°;
(2)2.
【分析】(1)直接利用相似三角形的性质得出∠ACD=∠B,再结合已知条件得出答案;
(2)利用相似三角形的性质得出,进而得出答案.
【解答】解:(1)∵△ABC∽△ACD,
∴∠ACD=∠B,
∵CD平分∠ACB,∠ACD=35°,
∴∠ACD=∠DCB=∠B=35°,
∴∠ADC=35°+35°=70°;
(2)∵△ABC∽△ACD,
∴,
∵AD=3,BD=5,
∴,
解得:AC=2.
【点评】此题主要考查了相似三角形的性质,正确掌握相似三角形的性质是解题关键.
15.(2024秋 新民市期中)四边形的一条对角线把这个四边形分成两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线称为这个四边形的“理想对角线”.
(1)如图1,在四边形ABCD中,∠ABC=70°,AB=AD,AD∥BC,当∠ADC=145°时.求证:对角线BD是四边形ABCD的“理想对角线”.
(2)如图2,四边形ABCD中,AC平分∠BCD,当∠BCD与∠BAD满足什么关系时,对角线AC是四边形ABCD的“理想对角线”,请说明理由.
【考点】相似三角形的性质;全等三角形的判定与性质.
【专题】图形的相似;推理能力.
【答案】(1)证明见解析部分.
(2)当∠BAD∠BCD=180°时,对角线AC是四边形ABCD的“理想对角线”.证明见解析部分.
【分析】(1)利用两角对应相等证明△ABD∽△DBC,可得结论.
(2)如图2中,当∠BAD∠BCD=180°时,对角线AC是四边形ABCD的“理想对角线”.证明△ACB∽△DCA,可得结论.
【解答】(1)证明:如图1中,
∵AB=AD,
∴∠ABD=∠ADB,
∵AD∥BC,
∴∠ADB=∠DBC,
∴∠ABD=∠DBC∠ABC=35°,
∵∠ADC+∠C=180°,∠ADC=145°,
∴∠C=35°,
∴∠ADB=∠ABD=∠DBC=∠C=35°,
∴△ABD∽△DBC,
∴BD是四边形ABCD的“理想对角线”.
(2)解:如图2中,当∠BAD∠BCD=180°时,对角线AC是四边形ABCD的“理想对角线”.
理由:∵AC平分∠BCD,
∴∠ACB=∠ACD,
∵∠B+∠ACB+∠BAC=180°,∠BAD∠BCD=∠BAC+∠CAD+∠ACB=180°,
∴∠DAC=∠B,
∴△ACB∽△DCA,
∴对角线AC是四边形ABCD的“理想对角线”.
【点评】本题考查相似三角形的判定和性质,四边形的“理想对角线”的定义等知识,解题的关键是正确寻找相似三角形解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.夯实基础 相似三角形的性质
一.选择题(共5小题)
1.(2024秋 龙岗区期中)如图,带有刻度的直尺结合数轴作图,已知图中过点B和8的两条线段(两条线段的另一端在刻度尺上分别对应3和5)相互平行.若点A在数轴上表示的数是﹣2且点A与刻度尺上的0刻度重合,则AB的长度是( )
A.3 B.4 C.5 D.6
2.(2024秋 泉州期中)若两个相似三角形周长的比为2:3,则这两个三角形的面积比是( )
A.1:2 B.2:3 C.4:6 D.4:9
3.(2024秋 杨浦区期中)已知△ABC的三边都不相等,如果△ABC与△DEF相似,且∠B=∠D,那么下列等式一定不成立的是( )
A. B. C. D.
4.(2024 通海县模拟)如图,△OAB∽△OCD,OA:OC=3:2,△OAB与△OCD的面积分别是S1与S2,周长分别是C1与C2,则下列说法正确的是( )
A. B. C. D.
5.(2024 白银模拟)△ABC∽△A′B′C′,已知AB=5,A′B′=6,△ABC面积为10,那么另一个三角形的面积为( )
A.15 B.14.4 C.12 D.10.8
二.填空题(共5小题)
6.(2024秋 中原区校级期中)已知,在平面直角坐标系xOy中,直线y=2x+4与x轴、y轴相交于A、B两点,且点C的坐标为(6,4),连接AC,与y轴相交于点D,点E在x轴上,如果△ABD和△ACE相似,则点E的坐标为 .
7.(2024秋 济南期中)如图,已知△ADE∽△ABC,且AD:DB=2:3,则S△ADE:S△ABC= .
8.(2024秋 郑州校级期中)如图,已知三角形纸片ABC中,∠A=90°,AB=9,AC=12折叠纸片,使点A落在BC边上事物点D处,折痕为EF(点E在AB上,点F在AC上).若△BDE与△ABC相似.则折痕EF的长度等于 .
9.(2024 望花区三模)如图,在平面直角坐标系中,矩形ABOC的边OB,OC分别在x轴、y轴的正半轴上,点A的坐标为(8,6),点P在矩形ABOC的内部,点E在BO边上,且满足△PBE∽△CBO,当△APC是等腰三角形时,点P的坐标为 .
10.(2024秋 惠山区期中)如图,在等腰△ABC中,,∠BAC=120°,AD⊥BC于点D,点P是BC边上的一个动点,以AP为边向右作△APQ∽△ABC,连接DQ,则AD= ,DQ的最小值为 cm.
三.解答题(共5小题)
11.(2024秋 碑林区校级期中)如图,△ABC中,AB=7厘米,AC=15厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?
12.(2024秋 昌平区期中)如图,在矩形ABCD中,点EF分别在边AD,DC上,△ABE∽△DEF,AB=6,AE=9,DE=2.
(1)求EF的长.
(2)求证:∠BEF=90°.
13.(2024秋 沈丘县期末)如图1,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒3cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒2cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)(如图2)连接AQ,CP,若AQ⊥CP,求t的值.
14.(2024秋 武侯区校级期末)如图,已知△ABC∽△ACD.
(1)若CD平分∠ACB,∠ACD=35°,求∠ADC的度数;
(2)若AD=3,BD=5,求AC的长.
15.(2024秋 新民市期中)四边形的一条对角线把这个四边形分成两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线称为这个四边形的“理想对角线”.
(1)如图1,在四边形ABCD中,∠ABC=70°,AB=AD,AD∥BC,当∠ADC=145°时.求证:对角线BD是四边形ABCD的“理想对角线”.
(2)如图2,四边形ABCD中,AC平分∠BCD,当∠BCD与∠BAD满足什么关系时,对角线AC是四边形ABCD的“理想对角线”,请说明理由.
预习衔接.夯实基础 相似三角形的性质
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 龙岗区期中)如图,带有刻度的直尺结合数轴作图,已知图中过点B和8的两条线段(两条线段的另一端在刻度尺上分别对应3和5)相互平行.若点A在数轴上表示的数是﹣2且点A与刻度尺上的0刻度重合,则AB的长度是( )
A.3 B.4 C.5 D.6
【考点】相似三角形的性质;数轴.
【专题】计算题;数形结合;运算能力.
【答案】D
【分析】利用数轴知识和三角形相似的性质解答.
【解答】解:∵由题意可知线段平行,
∴可以找到相似三角形,通过三角形相似可以得到相似比的等式,
,
,
AB=6.
故选:D.
【点评】本题考查了数轴和三角形相似的性质,解题的关键是掌握数轴知识和三角形相似的性质.
2.(2024秋 泉州期中)若两个相似三角形周长的比为2:3,则这两个三角形的面积比是( )
A.1:2 B.2:3 C.4:6 D.4:9
【考点】相似三角形的性质.
【专题】图形的相似;推理能力.
【答案】D
【分析】相似三角形周长的比等于相似比,相似三角形面积的比等于相似比的平方,由此即可计算.
【解答】解:∵两个相似三角形的周长比为2:3,
∴两个相似三角形的相似比为2:3,
∴这两个相似三角形的面积比为22:32=4:9.
故选:D.
【点评】本题主要考查相似三角形的性质,关键是掌握相似三角形的性质:相似三角形面积的比等于相似比的平方.
3.(2024秋 杨浦区期中)已知△ABC的三边都不相等,如果△ABC与△DEF相似,且∠B=∠D,那么下列等式一定不成立的是( )
A. B. C. D.
【考点】相似三角形的性质.
【专题】图形的相似;推理能力.
【答案】C
【分析】根据相似三角形的性质解答即可.
【解答】解:∵△ABC与△DEF相似,且∠B=∠D,
∴△ABC∽△EDF或△ABC∽△FDE,
当△ABC∽△EDF时,
,,故A、D正确,不符合题意;
当△ABC∽△FDE时,
,故B正确,不符合题意;
两组相似三角形中BC,EF均不是对应边,故C一定不成立.
故选:C.
【点评】本题考查的是相似三角形的性质,熟知相似三角形的对应边成比例,对应角相等是解题的关键.
4.(2024 通海县模拟)如图,△OAB∽△OCD,OA:OC=3:2,△OAB与△OCD的面积分别是S1与S2,周长分别是C1与C2,则下列说法正确的是( )
A. B. C. D.
【考点】相似三角形的性质.
【专题】图形的相似;几何直观.
【答案】A
【分析】根据相似三角形的性质判断即可.
【解答】解:∵△OAB∽△OCD,OA:OC=3:2,
∴,A正确;
∴,B错误;
∴,C错误;
∴OA:OC=3:2,D错误;
故选:A.
【点评】本题考查了相似三角形的性质,熟练掌握相似三角形的性质定理是解题的关键.
5.(2024 白银模拟)△ABC∽△A′B′C′,已知AB=5,A′B′=6,△ABC面积为10,那么另一个三角形的面积为( )
A.15 B.14.4 C.12 D.10.8
【考点】相似三角形的性质.
【答案】B
【分析】利用相似三角形的性质得出两三角形的面积比,进而求出即可.
【解答】解:∵△ABC∽△A′B′C′,AB=5,A′B′=6,
∴,
∵△ABC面积为10,
∴解得:S△A′B′C′=14.4.
故选:B.
【点评】此题主要考查了相似三角形的性质,利用相似比与面积比的关系得出是解题关键.
二.填空题(共5小题)
6.(2024秋 中原区校级期中)已知,在平面直角坐标系xOy中,直线y=2x+4与x轴、y轴相交于A、B两点,且点C的坐标为(6,4),连接AC,与y轴相交于点D,点E在x轴上,如果△ABD和△ACE相似,则点E的坐标为 (4,0)或(,0) .
【考点】相似三角形的性质;一次函数的性质;一次函数图象上点的坐标特征.
【专题】图形的相似;推理能力.
【答案】(4,0)或(,0).
【分析】首先根据一次函数确定点A(﹣2,0),B(0,4),然后根据点C判定BC∥x轴,进而得出∠C=∠CAE,然后根据相似三角形的判定方法列比例式解答即可.
【解答】解:当x=0时,则y=2x+4=4,
当y=0时,则2x+4=0,解得x=﹣2;
∴A点的坐标为(﹣2,0),B点的坐标为(0,4),
∵C(6,4),
∴BC∥x轴,BC=6,AC4,
∴∠C=∠CAE,
如果△ABD和△ACE相似,
则或,
即或,
解得AE=6或AE,
∴OE=4或OE,
∴点E的坐标为:(4,0)或(,0).
【点评】本题考查了坐标与图形,相似三角形的判定与性质,掌握相似三角形判定方法是解题的关键.
7.(2024秋 济南期中)如图,已知△ADE∽△ABC,且AD:DB=2:3,则S△ADE:S△ABC= .
【考点】相似三角形的性质.
【专题】图形的相似;推理能力.
【答案】.
【分析】先根据题意得出相似三角形的相似比,进而可得出结论.
【解答】解:∵△ADE∽△ABC,且AD:DB=2:3,
∴,
∴()2,
故答案为:.
【点评】本题考查的是相似三角形的性质,熟知相似三角形面积的比等于相似比的平方是解题的关键.
8.(2024秋 郑州校级期中)如图,已知三角形纸片ABC中,∠A=90°,AB=9,AC=12折叠纸片,使点A落在BC边上事物点D处,折痕为EF(点E在AB上,点F在AC上).若△BDE与△ABC相似.则折痕EF的长度等于 或4 .
【考点】相似三角形的性质;翻折变换(折叠问题).
【专题】图形的相似;推理能力.
【答案】见试题解答内容
【分析】若△BDE与△ABC相似,则∠BED=90°或∠BDE=90°,
①当∠BED=90°时,根据相似三角形的性质即可得到结论;②当∠BDE=90°时,由折叠的性质得,∠EDF=∠A=90°,则点F在BC上,这与题意不符.
【解答】解:若△BDE与△ABC相似,则∠BED=90°或∠BDE=90°,
①当∠BED=90°时,∵∠A=90°,
∴DE∥AC,
∴,
由折叠的性质得,DE=AE,∠AEF=∠DEF,
∴,
解得:AE,
∵DE∥AC,
∴∠AFE=∠DEF,
∴∠AEF=∠AFE,
∴△AEF是等腰直角三角形,
∴EFAE;
②当∠BDE=90°时,
由折叠的性质得,∠EDF=∠A=90°,
则点F与点C重合,
∵∠A=90°,AB=9,AC=12,
∴BC15,
∵∠A=∠EDB=90°,∠B=∠B,
∴△BDE∽△BAC,
∴,
∴,
∴DE=4,
∴AE=4,
∴EF4,
综上所述,折痕EF的长度等于或4,
故答案为:或4.
【点评】本题考查了相似三角形的性质,等腰直角三角形的判断和现在,折叠的性质,正确的理解题意是解题的关键.
9.(2024 望花区三模)如图,在平面直角坐标系中,矩形ABOC的边OB,OC分别在x轴、y轴的正半轴上,点A的坐标为(8,6),点P在矩形ABOC的内部,点E在BO边上,且满足△PBE∽△CBO,当△APC是等腰三角形时,点P的坐标为 (,)或(4,3) .
【考点】相似三角形的性质;坐标与图形性质;等腰三角形的性质;矩形的性质.
【专题】矩形 菱形 正方形;图形的相似;推理能力.
【答案】(,)或(4,3).
【分析】由题意得出P点在AC的垂直平分线上或在以点C为圆心AC为半径的圆弧上,由此分两种情形分别求解,可得结论.
【解答】解:∵点P在矩形ABOC的内部,且△APC是等腰三角形,
∴P点在AC的垂直平分线上或在以点C为圆心AC为半径的圆弧上;
①当P点在AC的垂直平分线上时,点P同时在BC上,AC的垂直平分线与BO的交点即是E,如图1所示:
∵PE⊥BO,CO⊥BO,
∴PE∥CO,
∴△PBE∽△CBO,
∵四边形ABOC是矩形,A点的坐标为(8,6),
∴点P横坐标为4,OC=6,BO=8,BE=4,
∵△PBE∽△CBO,
∴,即,
解得:PE=3,
∴点P(4,3);
②P点在以点C为圆心AC为半径的圆弧上,圆弧与BC的交点为P,
过点P作PE⊥BO于E,如图2所示:
∵CO⊥BO,
∴PE∥CO,
∴△PBE∽△CBO,
∵四边形ABOC是矩形,A点的坐标为(8,6),
∴AC=BO=8,CP=8,AB=OC=6,
∴BC10,
∴BP=2,
∵△PBE∽△CBO,
∴,即:,
解得:PE,BE,
∴OE=8,
∴点P(,);
综上所述:点P的坐标为:(,)或(4,3);
故答案为:(,)或(4,3).
【点评】本题考查了相似三角形的判定与性质、矩形的性质、等腰三角形的判定与性质、坐标与图形的性质、平行线的判定、勾股定理、分类讨论等知识,熟练掌握相似三角形与等腰三角形的判定与性质是解题的关键.
10.(2024秋 惠山区期中)如图,在等腰△ABC中,,∠BAC=120°,AD⊥BC于点D,点P是BC边上的一个动点,以AP为边向右作△APQ∽△ABC,连接DQ,则AD= ,DQ的最小值为 cm.
【考点】相似三角形的性质;等腰三角形的性质.
【专题】等腰三角形与直角三角形;运算能力.
【答案】,.
【分析】,先证△ABP≌△ACQ,易得∠DCQ恒为60°,根据题意易得AD的值,根据点到直线的所有连线中,垂线段最短,可知DQ的最小值即为DH,进行求解即可.
【解答】解:连接CQ,过点D作DH⊥CQ,垂足为H,如图所示:
∵△APQ∽△ABC,
∴∠PAQ=∠BAC,AP:AB=AQ:AC,
∴∠BAP=∠CAQ,
∵AB=AC,
∴AP=AQ,
在△ABP和△ACQ中,
,
∴△ABP≌△ACQ(SAS),
∴∠ACQ=∠ACB,
∵∠BAC=120°,
∴∠ABC=∠ACB=30°,
∴∠ACQ=30°,
∴∠DCQ=60°,
∴∠CDH=30°,
∵AB=ACcm,∠BAC=120°,
∴AC=6,AD,
∵AD⊥BC,
∴CD=3,
∴CH,DH.
∴DQ的最小值即为.
故答案为:,.
【点评】本题考查相似三角形和等腰三角形的性质,在运动过程中找出Q的运动轨迹,并运用垂线段最短求解是解决本题的关键.
三.解答题(共5小题)
11.(2024秋 碑林区校级期中)如图,△ABC中,AB=7厘米,AC=15厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?
【考点】相似三角形的性质.
【专题】图形的相似;运算能力;推理能力.
【答案】运动时间是秒.
【分析】首先设运动了t秒,根据题意得:AP=2tcm,CQ=3tcm,然后分别从当△APQ∽△ABC与当△APQ∽△ACB时去分析得出t的值,再由“其中一个动点到端点时,另一个动点也相应停止运动”可得t的取值范围,即可得出答案.
【解答】解:设运动了t秒.
根据题意得:AP=2t cm,CQ=3t cm,则AQ=AC﹣CQ=(15﹣3t)cm,
当△APQ∽△ABC时,,
即,
解得,
当△APQ∽△ACB时,,
即,
解得,
∵其中一个动点到端点时,另一个动点也相应停止运动,
∴P点运动时长最多为秒,Q点运动时长最多为15÷3=5秒,
∴,
∵,,
∴,
故当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是秒.
【点评】此题考查了相似三角形的性质.相似三角形的对应边的比相等.
12.(2024秋 昌平区期中)如图,在矩形ABCD中,点EF分别在边AD,DC上,△ABE∽△DEF,AB=6,AE=9,DE=2.
(1)求EF的长.
(2)求证:∠BEF=90°.
【考点】相似三角形的性质;勾股定理的逆定理;矩形的性质.
【专题】几何综合题;推理能力.
【答案】见试题解答内容
【分析】(1)根据两三角形相似,得到对应边成比例,,结合已知条件,从而得到DF的长,利用直角三角形勾股定理,从而得到结果;
(2)利用两三角形相似,得到对应角相等,结合直角三角形两锐角互余,从而证得结果.
【解答】(1)解:∵△ABE∽△DEF,
∴,
∵AB=6,AE=9,DE=2,
∴,
∴DF=3,
∵矩形ABCD,
∴∠EDF=90°,
∴在Rt△DEF中,
;
(2)证明:∵△ABE∽△DEF,
∴∠ABE=∠DEF,
∵在Rt△ABE中,∠ABE+∠AEB=90°,
∴∠DEF+∠AEB=90°,
∴∠BEF=90°.
【点评】本题考查了三角形相似的性质,以及矩形性质,勾股定理的应用,关键是合理应用三角形相似的性质.
13.(2024秋 沈丘县期末)如图1,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒3cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒2cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)(如图2)连接AQ,CP,若AQ⊥CP,求t的值.
【考点】相似三角形的性质.
【专题】图形的相似;推理能力.
【答案】见试题解答内容
【分析】(1)根据勾股定理求出AB,分△BPQ∽△BAC、△BPQ∽△BCA两种情况,根据相似三角形的性质列出比例式,计算即可;
(2)过P作PM⊥BC于点M,AQ,CP交于点N,则有PB=5t,PM=3t,BQ=8﹣4t,根据△ACQ∽△CMP,得出AC:CM=CQ:MP,代入计算即可.
【解答】解:(1)①当△BPQ∽△BAC时,
∵,BP=3t,QC=2t,AB=10cm,BC=8cm,
∴,
∴,
②当△BPQ∽△BCA时,
∵,
∴,
∴;
∴或时,△BPQ与△ABC相似;
(2)如图所示,过P作PM⊥BC于点M,AQ,CP交于点N,
则有PB=3t,,,,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM且∠ACQ=∠PMC=90°,
∴△ACQ∽△CMP,
∴,
∴
解得:.
【点评】此题是相似形综合题,主要考查了相似三角形的判定与性质,勾股定理,直角三角形的性质,等腰三角形的性质,由三角形相似得出对应边成比例是解题的关键.
14.(2024秋 武侯区校级期末)如图,已知△ABC∽△ACD.
(1)若CD平分∠ACB,∠ACD=35°,求∠ADC的度数;
(2)若AD=3,BD=5,求AC的长.
【考点】相似三角形的性质.
【专题】图形的相似;推理能力.
【答案】(1)70°;
(2)2.
【分析】(1)直接利用相似三角形的性质得出∠ACD=∠B,再结合已知条件得出答案;
(2)利用相似三角形的性质得出,进而得出答案.
【解答】解:(1)∵△ABC∽△ACD,
∴∠ACD=∠B,
∵CD平分∠ACB,∠ACD=35°,
∴∠ACD=∠DCB=∠B=35°,
∴∠ADC=35°+35°=70°;
(2)∵△ABC∽△ACD,
∴,
∵AD=3,BD=5,
∴,
解得:AC=2.
【点评】此题主要考查了相似三角形的性质,正确掌握相似三角形的性质是解题关键.
15.(2024秋 新民市期中)四边形的一条对角线把这个四边形分成两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线称为这个四边形的“理想对角线”.
(1)如图1,在四边形ABCD中,∠ABC=70°,AB=AD,AD∥BC,当∠ADC=145°时.求证:对角线BD是四边形ABCD的“理想对角线”.
(2)如图2,四边形ABCD中,AC平分∠BCD,当∠BCD与∠BAD满足什么关系时,对角线AC是四边形ABCD的“理想对角线”,请说明理由.
【考点】相似三角形的性质;全等三角形的判定与性质.
【专题】图形的相似;推理能力.
【答案】(1)证明见解析部分.
(2)当∠BAD∠BCD=180°时,对角线AC是四边形ABCD的“理想对角线”.证明见解析部分.
【分析】(1)利用两角对应相等证明△ABD∽△DBC,可得结论.
(2)如图2中,当∠BAD∠BCD=180°时,对角线AC是四边形ABCD的“理想对角线”.证明△ACB∽△DCA,可得结论.
【解答】(1)证明:如图1中,
∵AB=AD,
∴∠ABD=∠ADB,
∵AD∥BC,
∴∠ADB=∠DBC,
∴∠ABD=∠DBC∠ABC=35°,
∵∠ADC+∠C=180°,∠ADC=145°,
∴∠C=35°,
∴∠ADB=∠ABD=∠DBC=∠C=35°,
∴△ABD∽△DBC,
∴BD是四边形ABCD的“理想对角线”.
(2)解:如图2中,当∠BAD∠BCD=180°时,对角线AC是四边形ABCD的“理想对角线”.
理由:∵AC平分∠BCD,
∴∠ACB=∠ACD,
∵∠B+∠ACB+∠BAC=180°,∠BAD∠BCD=∠BAC+∠CAD+∠ACB=180°,
∴∠DAC=∠B,
∴△ACB∽△DCA,
∴对角线AC是四边形ABCD的“理想对角线”.
【点评】本题考查相似三角形的判定和性质,四边形的“理想对角线”的定义等知识,解题的关键是正确寻找相似三角形解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
