4.8图形的位似(预习衔接.夯实基础.含解析)-2025-2026学年九年级上册数学北师大版
文档属性
| 名称 | 4.8图形的位似(预习衔接.夯实基础.含解析)-2025-2026学年九年级上册数学北师大版 |
|
|
| 格式 | docx | ||
| 文件大小 | 707.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 21:06:41 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
预习衔接.夯实基础 图形的位似
一.选择题(共5小题)
1.(2024秋 武强县期中)如图,△ABC与△DEF是位似图形,点O是位似中心.若OA=2AD,△ABC的周长为4,则△DEF的周长为( )
A.6 B.8 C.9 D.12
2.(2024秋 铁西区期中)如图,△ABC与△DEF位似,点O是位似中心,若OA:AD=1:2,DF﹣AC=8,则DF+AC为( )
A.8 B.12 C.16 D.18
3.(2024秋 城关区期中)如图,在正方形网格图中,△ABC与△A′B′C′是位似图形,则位似中心是( )
A.点R B.点P C.点Q D.点O
4.(2024 裕华区校级开学)如图,在平面直角坐标系中,已知点A(﹣3,6)、B(﹣9,﹣3),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(﹣1,2) B.(﹣9,18)
C.(﹣9,18)或(9,﹣18) D.(﹣1,2)或(1,﹣2)
5.(2024秋 滨湖区期中)如图,在直角坐标系中,点A的坐标为(2,3),点B的坐标为(3,0).以点O为位似中心,在第一象限内把△AOB按相似比2:1放大,得到△A′OB′,则A′,B′的坐标是( )
A., B.(4,5),(5,0)
C.(4,6),(6,0) D.(6,9),(9,0)
二.填空题(共5小题)
6.(2024秋 潍坊期中)如图,在直角坐标系中,△ABC与△DEF是位似图形,则它们位似中心的坐标是 .
7.(2024秋 武侯区校级期中)如图,已知△A1OB1与△A2OB2位似,且△A1OB1与△A2OB2的周长之比为1:2,点A1的坐标为(﹣1,2),则点A2的坐标为 .
8.(2024秋 长春期中)如图,以点A为位似中心的四边形ABCD和四边形AB′C′D′面积比为9:4,若AB=6,则AB′的长为 .
9.(2024秋 牧野区校级期末)如图所示,在△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(﹣2,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的3倍,设点B的对应点B′的横坐标是7,则点B的横坐标是 .
10.(2024秋 富锦市校级期末)在平面直角坐标系中,A(﹣2,4),B(1,3),现以原点O为位似中心画出A′B′,使A′B′与AB相似比为,则A的对应点A′的坐标为 .
三.解答题(共5小题)
11.(2024秋 鹤山市期中)如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)请按顺序写出点A,E,C的对应点的坐标,并说说对应点的坐标有哪些特征;A(2,3)与D ;B 与E(﹣1,﹣2);C(3,1)与F ;对应点坐标的特征是横坐标、纵坐标均 ;
(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a,b的值.
12.(2024秋 南安市期中)如图,在平面直角坐标系中,每个小正方形的边长都是1个单位长度,△ABC的顶点都在格点上.
(1)以原点O为位似中心,在第三象限内画出将△ABC放大为原来的2倍后的位似图形△A1B1C1;
(2)若△ABC的周长为k,则△A1B1C1的周长是 (用含k的代数式表示).
13.(2024秋 市中区期中)如图,在边长为1的小正方形组成的网格中建立平面直角坐标系,以原点O为位似中心,在第一象限内将△OAB放大到原来的2倍后得到△OA'B',其中A、B在图中格点上,点A、B的对应点分别为A′、B′.
(1)在第一象限内画出△OA'B';
(2)求△OA′B′的面积;
(3)若点P(m,n)在边OB上,直接写出点P位似后的对应点P1的坐标 .
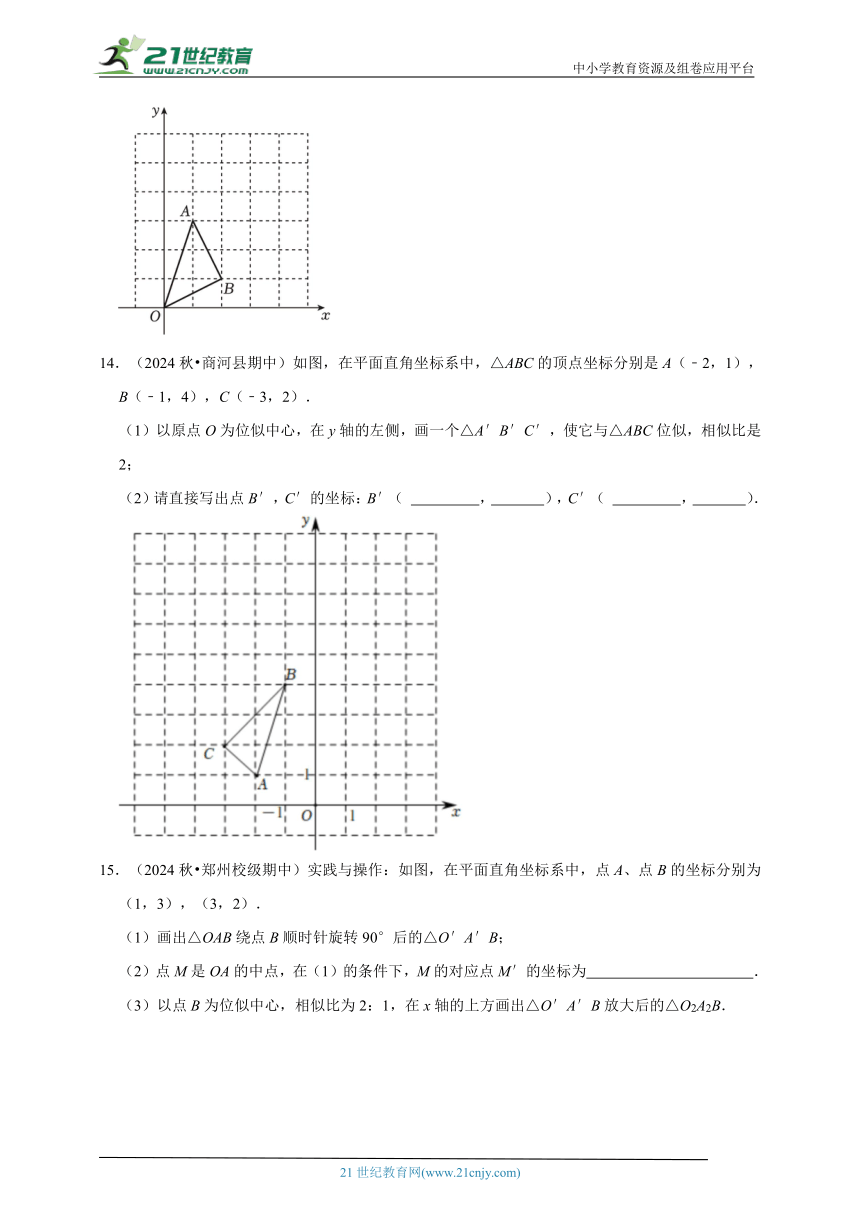
14.(2024秋 商河县期中)如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)以原点O为位似中心,在y轴的左侧,画一个△A′B′C′,使它与△ABC位似,相似比是2;
(2)请直接写出点B′,C′的坐标:B′( , ),C′( , ).
15.(2024秋 郑州校级期中)实践与操作:如图,在平面直角坐标系中,点A、点B的坐标分别为(1,3),(3,2).
(1)画出△OAB绕点B顺时针旋转90°后的△O′A′B;
(2)点M是OA的中点,在(1)的条件下,M的对应点M′的坐标为 .
(3)以点B为位似中心,相似比为2:1,在x轴的上方画出△O′A′B放大后的△O2A2B.
预习衔接.夯实基础 图形的位似
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 武强县期中)如图,△ABC与△DEF是位似图形,点O是位似中心.若OA=2AD,△ABC的周长为4,则△DEF的周长为( )
A.6 B.8 C.9 D.12
【考点】位似变换.
【专题】图形的相似;应用意识.
【答案】A
【分析】结合题意可得△ABC与△DEF的位似比为2:3,则△ABC与△DEF的周长比为2:3,进而可得答案.
【解答】解:∵OA=2AD,
∴OA:OD=2:3.
∵△ABC与△DEF是位似图形,点O是位似中心,
∴△ABC与△DEF的位似比为2:3,
∴△ABC与△DEF的周长比为2:3.
∵△ABC的周长为4,
∴△DEF的周长为6.
故选:A.
【点评】本题考查位似变换,熟练掌握位似的性质是解答本题的关键.
2.(2024秋 铁西区期中)如图,△ABC与△DEF位似,点O是位似中心,若OA:AD=1:2,DF﹣AC=8,则DF+AC为( )
A.8 B.12 C.16 D.18
【考点】位似变换.
【专题】图形的相似;几何直观;推理能力.
【答案】C
【分析】首先根据题意可知,再结合位似图形的性质可得,结合DF﹣AC=8解得AC、DF的值,进而可得答案.
【解答】解:△ABC与△DEF位似,点O是位似中心,OA:AD=1:2,
∴,
∴,
∴DF=3AC,
∵DF﹣AC=8,
∴3AC﹣AC=2AC=8,
解得AC=4,
∴DF=3AC=12,
∴DF+AC=12+4=16.
故选:C.
【点评】本题主要考查了位似变换,熟练掌握位似图形的定义和性质是解题关键.
3.(2024秋 城关区期中)如图,在正方形网格图中,△ABC与△A′B′C′是位似图形,则位似中心是( )
A.点R B.点P C.点Q D.点O
【考点】位似变换.
【专题】图形的相似;运算能力.
【答案】D
【分析】根据位似图形的概念,连接对应点,交点即是位似中心.
【解答】解:连接AA′,CC′,交于点O,
∴点O是位似中心,
故答案为:D.
【点评】本题考查确定位似中心,理解位似图形的概念是解题的关键.
4.(2024 裕华区校级开学)如图,在平面直角坐标系中,已知点A(﹣3,6)、B(﹣9,﹣3),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(﹣1,2) B.(﹣9,18)
C.(﹣9,18)或(9,﹣18) D.(﹣1,2)或(1,﹣2)
【考点】位似变换;坐标与图形性质.
【答案】D
【分析】根据在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k解答.
【解答】解:∵点A(﹣3,6),以原点O为位似中心,相似比为,把△ABO缩小,
∴点A的对应点A′的坐标是(﹣1,2)或(1,﹣2),
故选:D.
【点评】本题考查的是位似变换的概念和性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
5.(2024秋 滨湖区期中)如图,在直角坐标系中,点A的坐标为(2,3),点B的坐标为(3,0).以点O为位似中心,在第一象限内把△AOB按相似比2:1放大,得到△A′OB′,则A′,B′的坐标是( )
A., B.(4,5),(5,0)
C.(4,6),(6,0) D.(6,9),(9,0)
【考点】位似变换;坐标与图形性质.
【专题】图形的相似;推理能力.
【答案】C
【分析】根据关于以原点为位似中心的对称点的坐标特征,把点A、B的横纵坐标都乘以2得到点A′,B′的坐标.
【解答】解:∵以点O为位似中心,在第一象限内把△AOB按相似比2:1放大,得到△A′OB′,而点A的坐标为(2,3),点B的坐标为(3,0),
∴点A′的坐标为(2×2,2×3),点B′的坐标为(3×2,0×2),即点A′的坐标为(4,6),点B′的坐标为(6,0),
故选:C.
【点评】本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
二.填空题(共5小题)
6.(2024秋 潍坊期中)如图,在直角坐标系中,△ABC与△DEF是位似图形,则它们位似中心的坐标是 (0,2) .
【考点】位似变换;坐标与图形性质.
【专题】平面直角坐标系;图形的相似;几何直观.
【答案】(0,2).
【分析】直接利用位似图形的性质:对应点的连线都经过同一点,连接对应点,进而得出位似中心的位置.
【解答】解:如图所示:位似中心点P的坐标为(0,2).
故答案为:(0,2).
【点评】此题主要考查了位似变换,正确掌握位似图形的性质是解题关键.
7.(2024秋 武侯区校级期中)如图,已知△A1OB1与△A2OB2位似,且△A1OB1与△A2OB2的周长之比为1:2,点A1的坐标为(﹣1,2),则点A2的坐标为 (2,﹣4) .
【考点】位似变换;坐标与图形性质.
【专题】图形的相似;推理能力.
【答案】(2,﹣4).
【分析】利用相似的性质得到△A1OB1与△A2OB2的位似之比为1:2,然后把点A1的横纵坐标分别乘以﹣2得到点A2的坐标.
【解答】解:∵△A1OB1与△A2OB2的周长之比为1:2,
∴△A1OB1与△A2OB2的位似之比为1:2,
而点A1的坐标为(﹣1,2),
∴点A2的坐标为(2,﹣4).
故答案为:(2,﹣4).
【点评】本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
8.(2024秋 长春期中)如图,以点A为位似中心的四边形ABCD和四边形AB′C′D′面积比为9:4,若AB=6,则AB′的长为 4 .
【考点】位似变换.
【专题】图形的相似;几何直观;应用意识.
【答案】4.
【分析】由题意得四边形ABCD与四边形AB′C′D′的相似比为3:2,即AB:AB'=3:2,进而可得答案.
【解答】解:∵以点A为位似中心的四边形ABCD和四边形AB′C′D′面积比为9:4,
∴四边形ABCD与四边形AB′C′D′的相似比为3:2,
∴AB:AB'=3:2,
∵AB=6,
∴AB′=4.
故答案为:4.
【点评】本题考查位似变换,熟练掌握位似的性质是解答本题的关键.
9.(2024秋 牧野区校级期末)如图所示,在△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(﹣2,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的3倍,设点B的对应点B′的横坐标是7,则点B的横坐标是 ﹣5 .
【考点】位似变换;坐标与图形性质.
【专题】图形的相似;推理能力.
【答案】﹣5.
【分析】设点B的横坐标为x,则B、C间的横坐标的长度为﹣2﹣x,B′、C间的横坐标的长度为7﹣(﹣2)=9,然后根据位似图形的性质解答即可.
【解答】解:设点B的横坐标为x,则B、C间的横坐标的长度为﹣2﹣x,B′、C间的横坐标的长度为7﹣(﹣2)=9,
∵△ABC放大到原来的3倍得到△A′B′C,
∴3(﹣2﹣x)=9,
解得:x=﹣5,
故答案为:﹣5.
【点评】本题考查的是位似图形的性质,灵活运用位似图形坐标的性质列方程计算是解题的关键.
10.(2024秋 富锦市校级期末)在平面直角坐标系中,A(﹣2,4),B(1,3),现以原点O为位似中心画出A′B′,使A′B′与AB相似比为,则A的对应点A′的坐标为 (﹣1,2)或(1,﹣2) .
【考点】作图﹣位似变换.
【专题】图形的相似;推理能力.
【答案】见试题解答内容
【分析】利用关于以原点为位似中心的对应点的坐标特征,把点的A的横纵坐标都乘以或得到A的对应点A′的坐标.
【解答】解:∵以原点O为位似中心画出A′B′,使A′B′与AB相似比为,
而A(﹣2,4),
∴A的对应点A′的坐标为(﹣2,4)或[﹣2×(),4×()],
即(﹣1,2)或(1,﹣2).
故答案为:(﹣1,2)或(1,﹣2).
【点评】本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
三.解答题(共5小题)
11.(2024秋 鹤山市期中)如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)请按顺序写出点A,E,C的对应点的坐标,并说说对应点的坐标有哪些特征;A(2,3)与D (﹣2,﹣3) ;B (1,2) 与E(﹣1,﹣2);C(3,1)与F (﹣3,﹣1) ;对应点坐标的特征是横坐标、纵坐标均 互为相反数 ;
(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a,b的值.
【考点】几何变换的类型;坐标与图形性质.
【专题】平移、旋转与对称;几何直观.
【答案】(1)(﹣2,﹣3),(1,2),(﹣3,﹣1),互为相反数;
(2)a=﹣1,b=﹣1.
【分析】(1)根据点D,B,F的位置写出坐标即可;
(2)利用规律构建方程组求解.
【解答】解:(1)A(2,3)与D(﹣2,﹣3);B(1,2)与E(﹣1,﹣2);C(3,1)与F(﹣3,﹣1);
对应点坐标的特征是横坐标、纵坐标均互为相反数;
故答案为:(﹣2,﹣3),(1,2),(﹣3,﹣1),互为相反数;
(2)由题意,
解得.
∴a=﹣1,b=﹣1.
【点评】本题考查几何变换的类型,坐标与图形性质,解题的关键是掌握中心对称变换的性质,属于中考常考题型.
12.(2024秋 南安市期中)如图,在平面直角坐标系中,每个小正方形的边长都是1个单位长度,△ABC的顶点都在格点上.
(1)以原点O为位似中心,在第三象限内画出将△ABC放大为原来的2倍后的位似图形△A1B1C1;
(2)若△ABC的周长为k,则△A1B1C1的周长是 2k (用含k的代数式表示).
【考点】作图﹣位似变换.
【专题】作图题;图形的相似;几何直观.
【答案】(1)见解答.
(2)2k.
【分析】(1)根据位似的性质作图即可.
(2)由题意得,△ABC与△A1B1C1的相似比为1:2,则△ABC与△A1B1C1的周长比为1:2,进而可得答案.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)由题意得,△ABC与△A1B1C1的相似比为1:2,
∴△ABC与△A1B1C1的周长比为1:2,
∵△ABC的周长为k,
∴△A1B1C1的周长是2k.
故答案为:2k.
【点评】本题考查作图﹣位似变换,熟练掌握位似的性质是解答本题的关键.
13.(2024秋 市中区期中)如图,在边长为1的小正方形组成的网格中建立平面直角坐标系,以原点O为位似中心,在第一象限内将△OAB放大到原来的2倍后得到△OA'B',其中A、B在图中格点上,点A、B的对应点分别为A′、B′.
(1)在第一象限内画出△OA'B';
(2)求△OA′B′的面积;
(3)若点P(m,n)在边OB上,直接写出点P位似后的对应点P1的坐标 (2m,2n) .
【考点】作图﹣位似变换.
【专题】作图题;图形的相似;几何直观;运算能力.
【答案】(1)见解答.
(2)10.
(3)(2m,2n).
【分析】(1)根据位似的性质作图即可.
(2)利用割补法求三角形的面积即可.
(3)根据位似的性质可得答案.
【解答】解:(1)如图,△OA'B'即为所求.
(2)△OA′B′的面积为18﹣4﹣4=10.
(3)由题意得,点P位似后的对应点P1的坐标为(2m,2n).
故答案为:(2m,2n).
【点评】本题考查作图﹣位似变换,熟练掌握位似的性质是解答本题的关键.
14.(2024秋 商河县期中)如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)以原点O为位似中心,在y轴的左侧,画一个△A′B′C′,使它与△ABC位似,相似比是2;
(2)请直接写出点B′,C′的坐标:B′( ﹣2 , 8 ),C′( ﹣6 , 4 ).
【考点】作图﹣位似变换.
【专题】作图题;图形的相似;几何直观.
【答案】(1)作图见解析过程;
(2)﹣2;8;﹣6;4.
【分析】(1)根据位似即可得解;
(2)根据(1)中的图即可得解.
【解答】解:(1)如图,△A′B′C′即为所求.
(2)根据图得,B′(﹣2,8),C′(﹣6,4).
【点评】本题考查了作图﹣位似变换,解题的关键是理解题意,掌握位似.
15.(2024秋 郑州校级期中)实践与操作:如图,在平面直角坐标系中,点A、点B的坐标分别为(1,3),(3,2).
(1)画出△OAB绕点B顺时针旋转90°后的△O′A′B;
(2)点M是OA的中点,在(1)的条件下,M的对应点M′的坐标为 .
(3)以点B为位似中心,相似比为2:1,在x轴的上方画出△O′A′B放大后的△O2A2B.
【考点】作图﹣位似变换;作图﹣旋转变换.
【专题】作图题;几何直观.
【答案】(1)见解析;
(2);
(3)见解析.
【分析】(1)先作出点O、A绕点B顺时针旋转90°的对应点,然后再顺次连接即可;
(2)由题意得,点M′是O′A′的中点,利用中点坐标公式求解即可;
(3)根据位似的性质作图即可.
【解答】解:(1)如图,△O′A′B即为所求.
(2)∵点M是OA的中点,
∴点M′是O′A′的中点,
根据作图可知:O′(1,5),A′(4,4),
∴点M′的坐标为;
(3)如图,△O2A2B即为所求.
【点评】本题考查作图——旋转变换、位似变换、中点坐标公式,熟练掌握旋转和位似的性质是解答本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.夯实基础 图形的位似
一.选择题(共5小题)
1.(2024秋 武强县期中)如图,△ABC与△DEF是位似图形,点O是位似中心.若OA=2AD,△ABC的周长为4,则△DEF的周长为( )
A.6 B.8 C.9 D.12
2.(2024秋 铁西区期中)如图,△ABC与△DEF位似,点O是位似中心,若OA:AD=1:2,DF﹣AC=8,则DF+AC为( )
A.8 B.12 C.16 D.18
3.(2024秋 城关区期中)如图,在正方形网格图中,△ABC与△A′B′C′是位似图形,则位似中心是( )
A.点R B.点P C.点Q D.点O
4.(2024 裕华区校级开学)如图,在平面直角坐标系中,已知点A(﹣3,6)、B(﹣9,﹣3),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(﹣1,2) B.(﹣9,18)
C.(﹣9,18)或(9,﹣18) D.(﹣1,2)或(1,﹣2)
5.(2024秋 滨湖区期中)如图,在直角坐标系中,点A的坐标为(2,3),点B的坐标为(3,0).以点O为位似中心,在第一象限内把△AOB按相似比2:1放大,得到△A′OB′,则A′,B′的坐标是( )
A., B.(4,5),(5,0)
C.(4,6),(6,0) D.(6,9),(9,0)
二.填空题(共5小题)
6.(2024秋 潍坊期中)如图,在直角坐标系中,△ABC与△DEF是位似图形,则它们位似中心的坐标是 .
7.(2024秋 武侯区校级期中)如图,已知△A1OB1与△A2OB2位似,且△A1OB1与△A2OB2的周长之比为1:2,点A1的坐标为(﹣1,2),则点A2的坐标为 .
8.(2024秋 长春期中)如图,以点A为位似中心的四边形ABCD和四边形AB′C′D′面积比为9:4,若AB=6,则AB′的长为 .
9.(2024秋 牧野区校级期末)如图所示,在△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(﹣2,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的3倍,设点B的对应点B′的横坐标是7,则点B的横坐标是 .
10.(2024秋 富锦市校级期末)在平面直角坐标系中,A(﹣2,4),B(1,3),现以原点O为位似中心画出A′B′,使A′B′与AB相似比为,则A的对应点A′的坐标为 .
三.解答题(共5小题)
11.(2024秋 鹤山市期中)如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)请按顺序写出点A,E,C的对应点的坐标,并说说对应点的坐标有哪些特征;A(2,3)与D ;B 与E(﹣1,﹣2);C(3,1)与F ;对应点坐标的特征是横坐标、纵坐标均 ;
(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a,b的值.
12.(2024秋 南安市期中)如图,在平面直角坐标系中,每个小正方形的边长都是1个单位长度,△ABC的顶点都在格点上.
(1)以原点O为位似中心,在第三象限内画出将△ABC放大为原来的2倍后的位似图形△A1B1C1;
(2)若△ABC的周长为k,则△A1B1C1的周长是 (用含k的代数式表示).
13.(2024秋 市中区期中)如图,在边长为1的小正方形组成的网格中建立平面直角坐标系,以原点O为位似中心,在第一象限内将△OAB放大到原来的2倍后得到△OA'B',其中A、B在图中格点上,点A、B的对应点分别为A′、B′.
(1)在第一象限内画出△OA'B';
(2)求△OA′B′的面积;
(3)若点P(m,n)在边OB上,直接写出点P位似后的对应点P1的坐标 .
14.(2024秋 商河县期中)如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)以原点O为位似中心,在y轴的左侧,画一个△A′B′C′,使它与△ABC位似,相似比是2;
(2)请直接写出点B′,C′的坐标:B′( , ),C′( , ).
15.(2024秋 郑州校级期中)实践与操作:如图,在平面直角坐标系中,点A、点B的坐标分别为(1,3),(3,2).
(1)画出△OAB绕点B顺时针旋转90°后的△O′A′B;
(2)点M是OA的中点,在(1)的条件下,M的对应点M′的坐标为 .
(3)以点B为位似中心,相似比为2:1,在x轴的上方画出△O′A′B放大后的△O2A2B.
预习衔接.夯实基础 图形的位似
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 武强县期中)如图,△ABC与△DEF是位似图形,点O是位似中心.若OA=2AD,△ABC的周长为4,则△DEF的周长为( )
A.6 B.8 C.9 D.12
【考点】位似变换.
【专题】图形的相似;应用意识.
【答案】A
【分析】结合题意可得△ABC与△DEF的位似比为2:3,则△ABC与△DEF的周长比为2:3,进而可得答案.
【解答】解:∵OA=2AD,
∴OA:OD=2:3.
∵△ABC与△DEF是位似图形,点O是位似中心,
∴△ABC与△DEF的位似比为2:3,
∴△ABC与△DEF的周长比为2:3.
∵△ABC的周长为4,
∴△DEF的周长为6.
故选:A.
【点评】本题考查位似变换,熟练掌握位似的性质是解答本题的关键.
2.(2024秋 铁西区期中)如图,△ABC与△DEF位似,点O是位似中心,若OA:AD=1:2,DF﹣AC=8,则DF+AC为( )
A.8 B.12 C.16 D.18
【考点】位似变换.
【专题】图形的相似;几何直观;推理能力.
【答案】C
【分析】首先根据题意可知,再结合位似图形的性质可得,结合DF﹣AC=8解得AC、DF的值,进而可得答案.
【解答】解:△ABC与△DEF位似,点O是位似中心,OA:AD=1:2,
∴,
∴,
∴DF=3AC,
∵DF﹣AC=8,
∴3AC﹣AC=2AC=8,
解得AC=4,
∴DF=3AC=12,
∴DF+AC=12+4=16.
故选:C.
【点评】本题主要考查了位似变换,熟练掌握位似图形的定义和性质是解题关键.
3.(2024秋 城关区期中)如图,在正方形网格图中,△ABC与△A′B′C′是位似图形,则位似中心是( )
A.点R B.点P C.点Q D.点O
【考点】位似变换.
【专题】图形的相似;运算能力.
【答案】D
【分析】根据位似图形的概念,连接对应点,交点即是位似中心.
【解答】解:连接AA′,CC′,交于点O,
∴点O是位似中心,
故答案为:D.
【点评】本题考查确定位似中心,理解位似图形的概念是解题的关键.
4.(2024 裕华区校级开学)如图,在平面直角坐标系中,已知点A(﹣3,6)、B(﹣9,﹣3),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(﹣1,2) B.(﹣9,18)
C.(﹣9,18)或(9,﹣18) D.(﹣1,2)或(1,﹣2)
【考点】位似变换;坐标与图形性质.
【答案】D
【分析】根据在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k解答.
【解答】解:∵点A(﹣3,6),以原点O为位似中心,相似比为,把△ABO缩小,
∴点A的对应点A′的坐标是(﹣1,2)或(1,﹣2),
故选:D.
【点评】本题考查的是位似变换的概念和性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
5.(2024秋 滨湖区期中)如图,在直角坐标系中,点A的坐标为(2,3),点B的坐标为(3,0).以点O为位似中心,在第一象限内把△AOB按相似比2:1放大,得到△A′OB′,则A′,B′的坐标是( )
A., B.(4,5),(5,0)
C.(4,6),(6,0) D.(6,9),(9,0)
【考点】位似变换;坐标与图形性质.
【专题】图形的相似;推理能力.
【答案】C
【分析】根据关于以原点为位似中心的对称点的坐标特征,把点A、B的横纵坐标都乘以2得到点A′,B′的坐标.
【解答】解:∵以点O为位似中心,在第一象限内把△AOB按相似比2:1放大,得到△A′OB′,而点A的坐标为(2,3),点B的坐标为(3,0),
∴点A′的坐标为(2×2,2×3),点B′的坐标为(3×2,0×2),即点A′的坐标为(4,6),点B′的坐标为(6,0),
故选:C.
【点评】本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
二.填空题(共5小题)
6.(2024秋 潍坊期中)如图,在直角坐标系中,△ABC与△DEF是位似图形,则它们位似中心的坐标是 (0,2) .
【考点】位似变换;坐标与图形性质.
【专题】平面直角坐标系;图形的相似;几何直观.
【答案】(0,2).
【分析】直接利用位似图形的性质:对应点的连线都经过同一点,连接对应点,进而得出位似中心的位置.
【解答】解:如图所示:位似中心点P的坐标为(0,2).
故答案为:(0,2).
【点评】此题主要考查了位似变换,正确掌握位似图形的性质是解题关键.
7.(2024秋 武侯区校级期中)如图,已知△A1OB1与△A2OB2位似,且△A1OB1与△A2OB2的周长之比为1:2,点A1的坐标为(﹣1,2),则点A2的坐标为 (2,﹣4) .
【考点】位似变换;坐标与图形性质.
【专题】图形的相似;推理能力.
【答案】(2,﹣4).
【分析】利用相似的性质得到△A1OB1与△A2OB2的位似之比为1:2,然后把点A1的横纵坐标分别乘以﹣2得到点A2的坐标.
【解答】解:∵△A1OB1与△A2OB2的周长之比为1:2,
∴△A1OB1与△A2OB2的位似之比为1:2,
而点A1的坐标为(﹣1,2),
∴点A2的坐标为(2,﹣4).
故答案为:(2,﹣4).
【点评】本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
8.(2024秋 长春期中)如图,以点A为位似中心的四边形ABCD和四边形AB′C′D′面积比为9:4,若AB=6,则AB′的长为 4 .
【考点】位似变换.
【专题】图形的相似;几何直观;应用意识.
【答案】4.
【分析】由题意得四边形ABCD与四边形AB′C′D′的相似比为3:2,即AB:AB'=3:2,进而可得答案.
【解答】解:∵以点A为位似中心的四边形ABCD和四边形AB′C′D′面积比为9:4,
∴四边形ABCD与四边形AB′C′D′的相似比为3:2,
∴AB:AB'=3:2,
∵AB=6,
∴AB′=4.
故答案为:4.
【点评】本题考查位似变换,熟练掌握位似的性质是解答本题的关键.
9.(2024秋 牧野区校级期末)如图所示,在△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(﹣2,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的3倍,设点B的对应点B′的横坐标是7,则点B的横坐标是 ﹣5 .
【考点】位似变换;坐标与图形性质.
【专题】图形的相似;推理能力.
【答案】﹣5.
【分析】设点B的横坐标为x,则B、C间的横坐标的长度为﹣2﹣x,B′、C间的横坐标的长度为7﹣(﹣2)=9,然后根据位似图形的性质解答即可.
【解答】解:设点B的横坐标为x,则B、C间的横坐标的长度为﹣2﹣x,B′、C间的横坐标的长度为7﹣(﹣2)=9,
∵△ABC放大到原来的3倍得到△A′B′C,
∴3(﹣2﹣x)=9,
解得:x=﹣5,
故答案为:﹣5.
【点评】本题考查的是位似图形的性质,灵活运用位似图形坐标的性质列方程计算是解题的关键.
10.(2024秋 富锦市校级期末)在平面直角坐标系中,A(﹣2,4),B(1,3),现以原点O为位似中心画出A′B′,使A′B′与AB相似比为,则A的对应点A′的坐标为 (﹣1,2)或(1,﹣2) .
【考点】作图﹣位似变换.
【专题】图形的相似;推理能力.
【答案】见试题解答内容
【分析】利用关于以原点为位似中心的对应点的坐标特征,把点的A的横纵坐标都乘以或得到A的对应点A′的坐标.
【解答】解:∵以原点O为位似中心画出A′B′,使A′B′与AB相似比为,
而A(﹣2,4),
∴A的对应点A′的坐标为(﹣2,4)或[﹣2×(),4×()],
即(﹣1,2)或(1,﹣2).
故答案为:(﹣1,2)或(1,﹣2).
【点评】本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
三.解答题(共5小题)
11.(2024秋 鹤山市期中)如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)请按顺序写出点A,E,C的对应点的坐标,并说说对应点的坐标有哪些特征;A(2,3)与D (﹣2,﹣3) ;B (1,2) 与E(﹣1,﹣2);C(3,1)与F (﹣3,﹣1) ;对应点坐标的特征是横坐标、纵坐标均 互为相反数 ;
(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a,b的值.
【考点】几何变换的类型;坐标与图形性质.
【专题】平移、旋转与对称;几何直观.
【答案】(1)(﹣2,﹣3),(1,2),(﹣3,﹣1),互为相反数;
(2)a=﹣1,b=﹣1.
【分析】(1)根据点D,B,F的位置写出坐标即可;
(2)利用规律构建方程组求解.
【解答】解:(1)A(2,3)与D(﹣2,﹣3);B(1,2)与E(﹣1,﹣2);C(3,1)与F(﹣3,﹣1);
对应点坐标的特征是横坐标、纵坐标均互为相反数;
故答案为:(﹣2,﹣3),(1,2),(﹣3,﹣1),互为相反数;
(2)由题意,
解得.
∴a=﹣1,b=﹣1.
【点评】本题考查几何变换的类型,坐标与图形性质,解题的关键是掌握中心对称变换的性质,属于中考常考题型.
12.(2024秋 南安市期中)如图,在平面直角坐标系中,每个小正方形的边长都是1个单位长度,△ABC的顶点都在格点上.
(1)以原点O为位似中心,在第三象限内画出将△ABC放大为原来的2倍后的位似图形△A1B1C1;
(2)若△ABC的周长为k,则△A1B1C1的周长是 2k (用含k的代数式表示).
【考点】作图﹣位似变换.
【专题】作图题;图形的相似;几何直观.
【答案】(1)见解答.
(2)2k.
【分析】(1)根据位似的性质作图即可.
(2)由题意得,△ABC与△A1B1C1的相似比为1:2,则△ABC与△A1B1C1的周长比为1:2,进而可得答案.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)由题意得,△ABC与△A1B1C1的相似比为1:2,
∴△ABC与△A1B1C1的周长比为1:2,
∵△ABC的周长为k,
∴△A1B1C1的周长是2k.
故答案为:2k.
【点评】本题考查作图﹣位似变换,熟练掌握位似的性质是解答本题的关键.
13.(2024秋 市中区期中)如图,在边长为1的小正方形组成的网格中建立平面直角坐标系,以原点O为位似中心,在第一象限内将△OAB放大到原来的2倍后得到△OA'B',其中A、B在图中格点上,点A、B的对应点分别为A′、B′.
(1)在第一象限内画出△OA'B';
(2)求△OA′B′的面积;
(3)若点P(m,n)在边OB上,直接写出点P位似后的对应点P1的坐标 (2m,2n) .
【考点】作图﹣位似变换.
【专题】作图题;图形的相似;几何直观;运算能力.
【答案】(1)见解答.
(2)10.
(3)(2m,2n).
【分析】(1)根据位似的性质作图即可.
(2)利用割补法求三角形的面积即可.
(3)根据位似的性质可得答案.
【解答】解:(1)如图,△OA'B'即为所求.
(2)△OA′B′的面积为18﹣4﹣4=10.
(3)由题意得,点P位似后的对应点P1的坐标为(2m,2n).
故答案为:(2m,2n).
【点评】本题考查作图﹣位似变换,熟练掌握位似的性质是解答本题的关键.
14.(2024秋 商河县期中)如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)以原点O为位似中心,在y轴的左侧,画一个△A′B′C′,使它与△ABC位似,相似比是2;
(2)请直接写出点B′,C′的坐标:B′( ﹣2 , 8 ),C′( ﹣6 , 4 ).
【考点】作图﹣位似变换.
【专题】作图题;图形的相似;几何直观.
【答案】(1)作图见解析过程;
(2)﹣2;8;﹣6;4.
【分析】(1)根据位似即可得解;
(2)根据(1)中的图即可得解.
【解答】解:(1)如图,△A′B′C′即为所求.
(2)根据图得,B′(﹣2,8),C′(﹣6,4).
【点评】本题考查了作图﹣位似变换,解题的关键是理解题意,掌握位似.
15.(2024秋 郑州校级期中)实践与操作:如图,在平面直角坐标系中,点A、点B的坐标分别为(1,3),(3,2).
(1)画出△OAB绕点B顺时针旋转90°后的△O′A′B;
(2)点M是OA的中点,在(1)的条件下,M的对应点M′的坐标为 .
(3)以点B为位似中心,相似比为2:1,在x轴的上方画出△O′A′B放大后的△O2A2B.
【考点】作图﹣位似变换;作图﹣旋转变换.
【专题】作图题;几何直观.
【答案】(1)见解析;
(2);
(3)见解析.
【分析】(1)先作出点O、A绕点B顺时针旋转90°的对应点,然后再顺次连接即可;
(2)由题意得,点M′是O′A′的中点,利用中点坐标公式求解即可;
(3)根据位似的性质作图即可.
【解答】解:(1)如图,△O′A′B即为所求.
(2)∵点M是OA的中点,
∴点M′是O′A′的中点,
根据作图可知:O′(1,5),A′(4,4),
∴点M′的坐标为;
(3)如图,△O2A2B即为所求.
【点评】本题考查作图——旋转变换、位似变换、中点坐标公式,熟练掌握旋转和位似的性质是解答本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
