1.1同底数幂的乘法 课件(共24张PPT) 北师大版(2024)数学七年级下册
文档属性
| 名称 | 1.1同底数幂的乘法 课件(共24张PPT) 北师大版(2024)数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 18.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 14:02:47 | ||
图片预览






文档简介
(共24张PPT)
同底数幂的乘法
2025
年 级:七年级 学 科:数学(北师版)
- 目录 -
01
05
02
06
03
04
数学概念引入
课堂练习与巩固
同底数幂乘法法则
法则的应用实例
法则的拓展与深化
数学文化与历史
数学概念引入
Part.
01
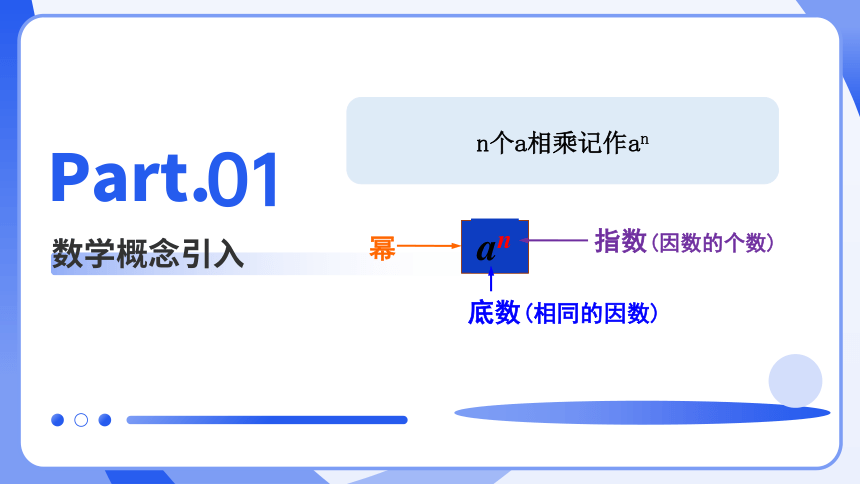
an
幂
底数(相同的因数)
指数(因数的个数)
n个a相乘记作an
幂的数学表达
幂是数学中表示重复乘法运算的结果,通常写作an,其中a为底数,n为指数。底数a可以是任何实数,指数n表示a自乘的次数。例如,23=2×2×2=8。幂的运算在科学计算、工程技术和日常生活中有着广泛的应用。
幂的运算意义
幂的运算不仅简化了重复乘法的表示,还为解决实际问题提供了便利。例如,在计算面积、体积时,幂运算能快速得出结果。此外,幂运算在计算机科学中用于表示数据存储容量,如KB、MB、GB等单位之间的转换,都依赖于幂的运算规则。
幂的定义与基本性质
同底数幂乘法法则
Part.
02
法则的推导过程
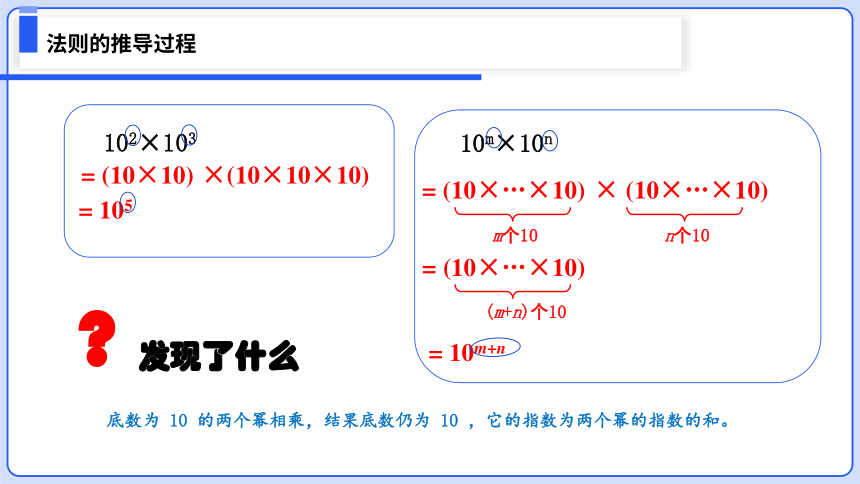
102×103 等于多少?
10m×10n(m,n 都是正整数)等于多少?
法则的推导过程
102×103
×(10×10×10)
= 105
= (10×10)
10m×10n
= (10×…×10)
m个10
× (10×…×10)
n个10
= (10×…×10)
(m+n)个10
= 10m+n
底数为 10 的两个幂相乘,结果底数仍为 10 ,它的指数为两个幂的指数的和。
发现了什么
观察具体案例
通过具体的例子,我们可以观察到同底数幂相乘的规律。例如,计算102×103时,可以展开为(10×10)×(10×10×10),结果为10(2+3)=105。这个例子展示了同底数幂相乘时,底数保持不变,指数相加的规律,这是同底数幂乘法法则的基础。
法则的推导过程
法则的推导过程
如果 m、n 都是正整数,那么 am·an 等于什么 为什么 与同伴进行交流。
am · an
m 个 a
n 个 a
=( a · a · … · a )·( a · a · … · a)
= am+n。
通过刚才的计算,你发现了什么?
在观察多个具体案例后,我们可以归纳出同底数幂乘法的一般规律:对于任何非零实数a和正整数m、n,有am×an=a(m+n)。这个规律不仅适用于正整数指数,也适用于零指数和负整数指数,是幂运算的重要性质之一。
归纳一般规律
法则的推导过程
法则的推导过程
不变
相加
am · an = am+n(m,n 都是正整数)
同底数幂的乘法法则:
运用法则的前提条件:
①底数相同;
②乘法运算。
两者缺一不可
同底数幂相乘,底数_____,指数_____。
练一练
例1计算:
(1)7×73×711
(2)(-2)3×(-2)5
(3)-y4×y5
(4)a3n×a3n-1
练一练
解:(1)7×73×711=71+3+11=715
(2)(-2)3×(-2)5=(-2)3+5=28
(3)-y4×y5=-y4+5=-y9
(4)a3n×a3n-1=a3n+3n-1=a6n-1
法则的应用实例
Part.
03
在计算几何图形的面积和体积时,同底数幂乘法法则非常实用。例如,计算一个边长为23米的正方形的面积为多少?
计算面积与体积
实际问题中的应用
解:23×23=23+3=26(平方米)
答:一个边长为23米的正方形的面积为26平方米
计算面积与体积
实际问题中的应用
3个及以上的同底数幂相乘,底数不变,指数相加
am · an · ap=am +n+p
同样,计算一个边长为22米的立方体的体积为多少?
解:22×22×22=22+2+2=26(立方米)
答:一个边长为22米的立方体的体积为26立方米
在计算机科学中,数据存储容量的计算也离不开同底数幂乘法法则。例如,1KB=210字节,1MB=220字节,1GB=230字节。当需要计算多个存储单元的总容量时,可以利用同底数幂相乘的法则,快速得出结果,如210×220=210+20=230字节=1GB。
数据存储容量计算
实际问题中的应用
法则的拓展与深化
Part.
04
负整数指数的意义
负整数指数幂是同底数幂乘法法则的拓展,它表示底数的倒数的正整数次幂。例如,2- 3=1/(23)=1/8。负整数指数幂在科学计算中有着重要的应用,如表示微小量的单位换算,或在电子工程中表示电阻、电容等元件的参数。
负整数指数幂的应用
负整数指数的运算规则
同底数幂乘法法则同样适用于负整数指数。例如,计算2- 3×24时,可以应用法则得到2(- 3+4)=21=2。这个规则不仅简化了运算过程,也加深了对幂运算的理解,为后续学习更复杂的数学概念打下了基础。
负整数指数幂的应用
课堂练习与巩固
Part.
05
课堂练习
1. 下面计算正确的是( )
A. (y – x)·(y – x)2·(y – x)3 = (x – y)6
B. (x – y)2·(y – x)3 = (x – y)6
C. (x – y)·(y – x)3·(x – y)2 = (x – y)6
D. (x – y)5·(y – x)2 = – (x – y)7
A
2. 计算: ______。
数学文化与历史
Part.
06
幂运算的历史可以追溯到古代文明。在古埃及和巴比伦的数学文献中,就已经出现了幂运算的雏形。例如,古埃及人使用幂运算来计算土地面积和建筑体积。这些早期的幂运算方法,为后来的数学发展奠定了基础,也展示了数学在人类文明中的重要作用。
古代数学中的幂运算
随着数学的发展,幂运算的规则和应用不断丰富。在现代数学中,幂运算不仅用于基础算术,还广泛应用于代数、几何、物理和工程等领域。例如,在计算机科学中,幂运算用于数据加密和算法设计;在物理学中,幂运算用于描述自然现象和解决实际问题。这些应用展示了幂运算的广泛性和重要性。
现代数学中的幂运算
幂运算的发展历程
同底数幂的乘法
2025
年 级:七年级 学 科:数学(北师版)
- 目录 -
01
05
02
06
03
04
数学概念引入
课堂练习与巩固
同底数幂乘法法则
法则的应用实例
法则的拓展与深化
数学文化与历史
数学概念引入
Part.
01
an
幂
底数(相同的因数)
指数(因数的个数)
n个a相乘记作an
幂的数学表达
幂是数学中表示重复乘法运算的结果,通常写作an,其中a为底数,n为指数。底数a可以是任何实数,指数n表示a自乘的次数。例如,23=2×2×2=8。幂的运算在科学计算、工程技术和日常生活中有着广泛的应用。
幂的运算意义
幂的运算不仅简化了重复乘法的表示,还为解决实际问题提供了便利。例如,在计算面积、体积时,幂运算能快速得出结果。此外,幂运算在计算机科学中用于表示数据存储容量,如KB、MB、GB等单位之间的转换,都依赖于幂的运算规则。
幂的定义与基本性质
同底数幂乘法法则
Part.
02
法则的推导过程
102×103 等于多少?
10m×10n(m,n 都是正整数)等于多少?
法则的推导过程
102×103
×(10×10×10)
= 105
= (10×10)
10m×10n
= (10×…×10)
m个10
× (10×…×10)
n个10
= (10×…×10)
(m+n)个10
= 10m+n
底数为 10 的两个幂相乘,结果底数仍为 10 ,它的指数为两个幂的指数的和。
发现了什么
观察具体案例
通过具体的例子,我们可以观察到同底数幂相乘的规律。例如,计算102×103时,可以展开为(10×10)×(10×10×10),结果为10(2+3)=105。这个例子展示了同底数幂相乘时,底数保持不变,指数相加的规律,这是同底数幂乘法法则的基础。
法则的推导过程
法则的推导过程
如果 m、n 都是正整数,那么 am·an 等于什么 为什么 与同伴进行交流。
am · an
m 个 a
n 个 a
=( a · a · … · a )·( a · a · … · a)
= am+n。
通过刚才的计算,你发现了什么?
在观察多个具体案例后,我们可以归纳出同底数幂乘法的一般规律:对于任何非零实数a和正整数m、n,有am×an=a(m+n)。这个规律不仅适用于正整数指数,也适用于零指数和负整数指数,是幂运算的重要性质之一。
归纳一般规律
法则的推导过程
法则的推导过程
不变
相加
am · an = am+n(m,n 都是正整数)
同底数幂的乘法法则:
运用法则的前提条件:
①底数相同;
②乘法运算。
两者缺一不可
同底数幂相乘,底数_____,指数_____。
练一练
例1计算:
(1)7×73×711
(2)(-2)3×(-2)5
(3)-y4×y5
(4)a3n×a3n-1
练一练
解:(1)7×73×711=71+3+11=715
(2)(-2)3×(-2)5=(-2)3+5=28
(3)-y4×y5=-y4+5=-y9
(4)a3n×a3n-1=a3n+3n-1=a6n-1
法则的应用实例
Part.
03
在计算几何图形的面积和体积时,同底数幂乘法法则非常实用。例如,计算一个边长为23米的正方形的面积为多少?
计算面积与体积
实际问题中的应用
解:23×23=23+3=26(平方米)
答:一个边长为23米的正方形的面积为26平方米
计算面积与体积
实际问题中的应用
3个及以上的同底数幂相乘,底数不变,指数相加
am · an · ap=am +n+p
同样,计算一个边长为22米的立方体的体积为多少?
解:22×22×22=22+2+2=26(立方米)
答:一个边长为22米的立方体的体积为26立方米
在计算机科学中,数据存储容量的计算也离不开同底数幂乘法法则。例如,1KB=210字节,1MB=220字节,1GB=230字节。当需要计算多个存储单元的总容量时,可以利用同底数幂相乘的法则,快速得出结果,如210×220=210+20=230字节=1GB。
数据存储容量计算
实际问题中的应用
法则的拓展与深化
Part.
04
负整数指数的意义
负整数指数幂是同底数幂乘法法则的拓展,它表示底数的倒数的正整数次幂。例如,2- 3=1/(23)=1/8。负整数指数幂在科学计算中有着重要的应用,如表示微小量的单位换算,或在电子工程中表示电阻、电容等元件的参数。
负整数指数幂的应用
负整数指数的运算规则
同底数幂乘法法则同样适用于负整数指数。例如,计算2- 3×24时,可以应用法则得到2(- 3+4)=21=2。这个规则不仅简化了运算过程,也加深了对幂运算的理解,为后续学习更复杂的数学概念打下了基础。
负整数指数幂的应用
课堂练习与巩固
Part.
05
课堂练习
1. 下面计算正确的是( )
A. (y – x)·(y – x)2·(y – x)3 = (x – y)6
B. (x – y)2·(y – x)3 = (x – y)6
C. (x – y)·(y – x)3·(x – y)2 = (x – y)6
D. (x – y)5·(y – x)2 = – (x – y)7
A
2. 计算: ______。
数学文化与历史
Part.
06
幂运算的历史可以追溯到古代文明。在古埃及和巴比伦的数学文献中,就已经出现了幂运算的雏形。例如,古埃及人使用幂运算来计算土地面积和建筑体积。这些早期的幂运算方法,为后来的数学发展奠定了基础,也展示了数学在人类文明中的重要作用。
古代数学中的幂运算
随着数学的发展,幂运算的规则和应用不断丰富。在现代数学中,幂运算不仅用于基础算术,还广泛应用于代数、几何、物理和工程等领域。例如,在计算机科学中,幂运算用于数据加密和算法设计;在物理学中,幂运算用于描述自然现象和解决实际问题。这些应用展示了幂运算的广泛性和重要性。
现代数学中的幂运算
幂运算的发展历程
同课章节目录
