【江苏专版】45 第十章 第4节 电磁感应中动量、能量和图像问题 课件《高考快车道》2026高考物理一轮总复习
文档属性
| 名称 | 【江苏专版】45 第十章 第4节 电磁感应中动量、能量和图像问题 课件《高考快车道》2026高考物理一轮总复习 |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-12-04 16:10:23 | ||
图片预览









文档简介
(共138张PPT)
第十章 电磁感应
第4节 电磁感应中动量、能量和图像问题
细研考点·突破题型
1.电磁感应中的能量转化
考点1 电磁感应中的能量问题
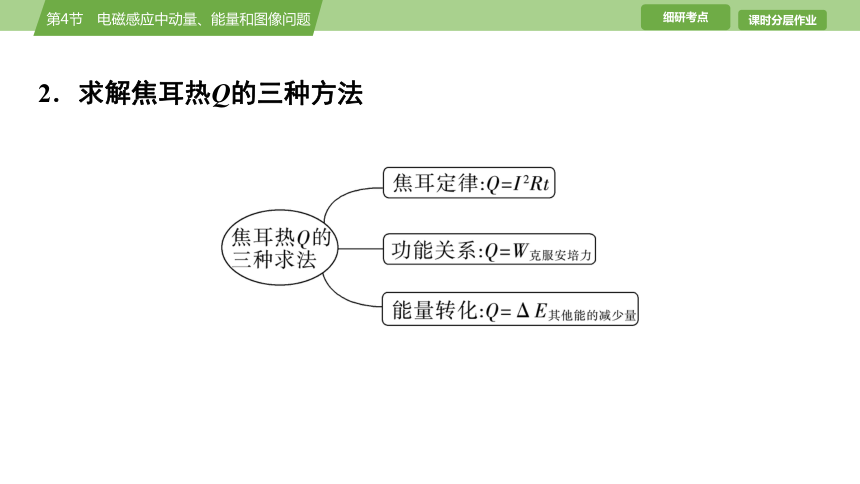
2.求解焦耳热Q的三种方法
3.求解电磁感应现象中能量问题的一般步骤
(1)在电磁感应中,切割磁感线的导体或磁通量发生变化的回路将产生感应电动势,该导体或回路就相当于电源。
(2)分析清楚有哪些力做功,就可以知道有哪些形式的能量发生了相互转化。
(3)根据能量守恒列方程求解。
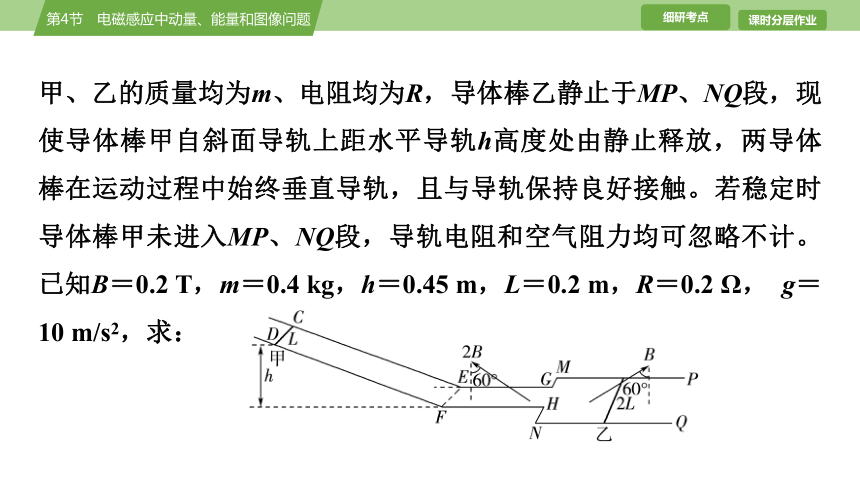
[典例1] (应用功能关系解决电磁感应中的能量问题)(2024·江苏南京模拟考试)如图所示,平行光滑的金属导轨由斜面和水平两部分组成,两部分导轨由两小段光滑、绝缘的圆弧轨道(长度可忽略)平滑相连。斜面部分(与水平面夹角小于30°)由间距为L的导轨CE、DF构成,水平部分由两段足够长但不等宽的平行金属导轨连接构成。EG、FH段间距为L,内有与竖直方向成60°角斜向左上方的磁感应强度大小为2B的匀强磁场。MP、NQ段间距为2L,内有与竖直方向成60°角斜向右上方的磁感应强度大小为B的匀强磁场。导体棒
甲、乙的质量均为m、电阻均为R,导体棒乙静止于MP、NQ段,现使导体棒甲自斜面导轨上距水平导轨h高度处由静止释放,两导体棒在运动过程中始终垂直导轨,且与导轨保持良好接触。若稳定时导体棒甲未进入MP、NQ段,导轨电阻和空气阻力均可忽略不计。已知B=0.2 T,m=0.4 kg,h=0.45 m,L=0.2 m,R=0.2 Ω, g=10 m/s2,求:
(1)甲棒刚进入磁场时,乙棒的加速度;
(2)从甲棒进入磁场到两棒达到稳定的过程,通过乙棒的电荷量;
(3)从甲棒进入磁场到两棒达到稳定的过程,乙棒上产生的焦耳热。
[解析] (1)甲棒在斜面导轨下滑的过程,由机械能守恒定律得mgh=
甲棒刚进入磁场时切割磁感线产生的感应电动势为
E1=2B cos 60°·Lv0
由闭合电路欧姆定律可知,回路中产生的感应电流为I1=
对乙棒,由牛顿第二定律可得
B cos 60°·I1·2L=ma
联立可得,乙棒的加速度大小为
a=0.03 m/s2,方向水平向右。
(2)两棒稳定时,电路中电流为0,则
2B cos 60°·Lv1=B cos 60°·2Lv2
解得v1=v2
两棒受到的安培力满足Fa=Fb
且安培力方向相反,则两棒组成的系统动量守恒,可得mv0=mv1+mv2
对乙棒,根据动量定理有B cos 60°··2Lt=mv2
其中q=t
联立可得,通过乙棒的电荷量为q=15 C。
(3)从甲棒进入磁场到两棒达到稳定的过程中,根据能量守恒定律有=+Q总
解得Q总=0.9 J
则乙棒上产生的焦耳热为Q乙=Q总=0.45 J。
[答案] (1)0.03 m/s2,方向水平向右 (2)15 C (3)0.45 J
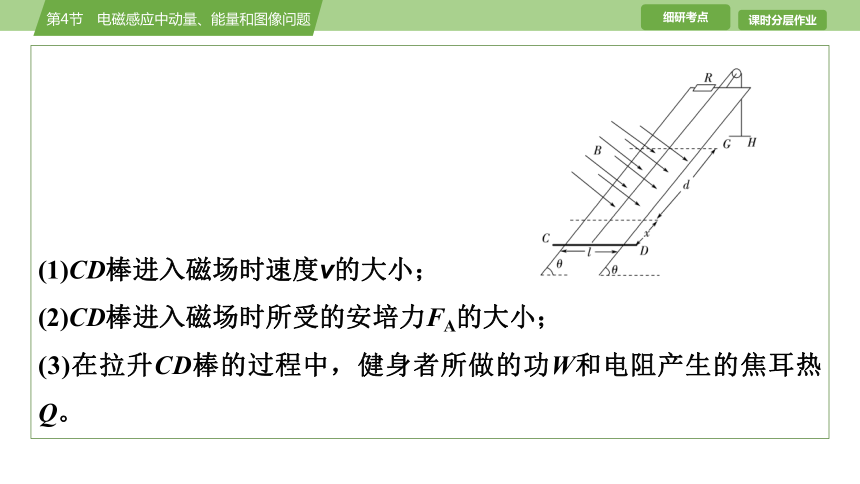
【典例1 教用·备选题】 (应用功能关系解决电磁感应中的能量问题)小明设计的电磁健身器的简化装置如图所示,两根平行金属导轨相距l=0.50 m,倾角θ=53°,导轨上端接一个R=0.05 Ω 的电阻。在导轨间长d=0.56 m 的区域内,存在方向垂直导轨平面向下的匀强磁场,磁感应强度B=2.0 T。质量m=4.0 kg的金属棒CD水平置于导轨上,用绝缘绳索通过定滑轮与拉杆GH相连。CD棒的初始位置与磁场区域的下边界相距x=0.24 m。 一位健身者用恒力F=80 N 拉动GH杆,CD棒由静止开始运动,上升过程中CD棒始终保持与导轨垂直。当CD棒到达磁场上边界时健身者松手,触发恢复装置使CD棒回到初始位置(重力加速度g取10 m/s2,sin 53°=0.8,不计其他电阻、摩擦力以及拉杆和绳索的质量)。求:
(1)CD棒进入磁场时速度v的大小;
(2)CD棒进入磁场时所受的安培力FA的大小;
(3)在拉升CD棒的过程中,健身者所做的功W和电阻产生的焦耳热Q。
[解析] (1)棒进入磁场前由牛顿第二定律有a==12 m/s2
进入磁场时的速度v==2.4 m/s。
(2)感应电动势E=Blv
感应电流I=
安培力FA=BIl
代入得FA==48 N。
(3)健身者做功W=F(x+d)=64 J
由牛顿第二定律得F-mg sin θ-FA=0
知CD棒在磁场区域做匀速运动
在磁场中运动时间为t=
焦耳热Q=I2Rt=26.88 J。
[答案] (1)2.4 m/s (2)48 N (3)64 J 26.88 J
[典例2] (应用能量守恒定律解决电磁感应中的能量问题)(2024·江苏淮阴中学模拟)如图所示,凸字形硬质金属线框质量为m,相邻各边互相垂直,且处于同一竖直平面内,ab边长为l,cd边长为2l,ab与cd平行,间距为2l。匀强磁场区域的上下边界均水平,磁场方向垂直于线框所在平面。开始时,cd边到磁场上边界的距离为2l,线框由静止释放,从cd边进入磁场直到ef、pq边进入磁场前,线框做匀速运动,在ef、pq边离开磁场后,ab边离开磁场之前,线框又做匀速运动。线框完全穿过磁场过程中产生的热量为Q。线框在下落过程中始终处于原竖直平面内,且ab、cd边保持水平,重力加速度为g。求:
(1)线框ab边将离开磁场时做匀速运动的速度大小是cd边刚进入磁场时的几倍;
(2)磁场上下边界间的距离H。
[解析] (1)设磁场的磁感应强度大小为B,cd边刚进入磁场时,线框做匀速运动的速度为v1,cd边上的感应电动势为E1,由法拉第电磁感应定律可得E1=2Blv1
设线框总电阻为R,此时线框中电流为I1,由闭合电路欧姆定律可得I1=
设此时线框所受安培力为F1,有F1=2I1lB
由于线框做匀速运动,故受力平衡,所以有mg=F1
联立解得v1=
设ab边离开磁场之前,线框做匀速运动的速度为v2,
同理可得v2=,故可知v2=4v1
即线框ab边将离开磁场时做匀速运动的速度大小是cd边刚进入磁场时的4倍。
(2)线框自释放直到cd边进入磁场前,由机械能守恒定律可得
2mgl=
线框完全穿过磁场的过程中,由能量守恒定律可得
mg(2l+H)=+Q
联立解得H=+28l。
[答案] (1)4倍 (2)+28l
【典例2 教用·备选题】 (应用能量守恒定律解决电磁感应中的能量问题)如图所示,竖直放置的“ ”形光滑导轨宽为L,矩形匀强磁场Ⅰ、Ⅱ的高和间距均为d,磁感应强度为B。质量为m的水平金属杆由静止释放,进入磁场Ⅰ和Ⅱ时的速度相等。金属杆在导轨间的电阻为R,与导轨接触良好,其余电阻不计,重力加速度为g。金属杆( )
A.刚进入磁场Ⅰ时加速度方向竖直向下
B.穿过磁场Ⅰ的时间小于在两磁场之间的运动时间
C.穿过两磁场产生的总热量为4mgd
D.释放时距磁场Ⅰ上边界的高度h可能小于
√
C [根据题述,由金属杆进入磁场Ⅰ和Ⅱ时的速度相等可知,金属杆在磁场Ⅰ中做减速运动,所以金属杆刚进入磁场Ⅰ时加速度方向竖直向上,A错误;由于金属杆进入磁场Ⅰ后做加速度逐渐减小的减速运动,而在两磁场之间做匀加速运动,所以穿过磁场Ⅰ的时间大于在两磁场之间的运动时间,B错误;根据能量守恒定律,金属杆从刚进入磁场Ⅰ到刚进入磁场Ⅱ过程动能变化量为0,重力做功为2mgd,则金属杆穿过磁场Ⅰ产生的热量Q1=2mgd,而金属杆在两磁场区域的运动情况相同,产生的热量相等,所以金属杆穿过两
磁场产生的总热量Q2=2×2mgd=4mgd,C正确;金属杆刚进入磁场Ⅰ时的速度v=,进入磁场Ⅰ时产生的感应电动势E=BLv,感应电流I=,所受安培力F=BIL,由于金属杆刚进入磁场Ⅰ时加速度方向竖直向上,所以安培力大于重力,即F>mg,联立解得h>,D错误。]
[典例3] (应用焦耳定律求电能) (2020·江苏卷)如图所示,电阻为0.1 Ω的正方形单匝线圈abcd的边长为0.2 m,bc边与匀强磁场边缘重合。磁场的宽度等于线圈的边长,磁感应强度大小为0.5 T,在水平拉力作用下,线圈以8 m/s的速度向右穿过磁场区域。求线圈在上述过程中:
(1)感应电动势的大小E;
(2)所受拉力的大小F;
(3)感应电流产生的热量Q。
[解析] (1)线圈切割磁感线产生的感应电动势 E=Blv
代入数据得E=0.8 V。
(2)线圈中产生的感应电流I=
拉力的大小等于安培力的大小,则F=BIl
解得F=
代入数据得F=0.8 N。
(3)运动时间t=
根据焦耳定律有Q=I2Rt
联立可得Q=
代入数据解得Q=0.32 J。
[答案] (1)0.8 V (2)0.8 N (3)0.32 J
【典例3 教用·备选题】 (应用焦耳定律求电能)光滑绝缘的水平面上有垂直于水平面的匀强磁场,磁场被分成区域Ⅰ和Ⅱ,宽度均为h,其俯视图如图(a)所示,两磁场磁感应强度随时间t的变化如图(b)所示,0~τ时间内,两区域磁场恒定,方向相反,磁感应强度大小分别为2B0和B0,一电阻为R、边长为h的刚性正方形金属框abcd平放在水平面上,ab、cd边与磁场边界平行。t=0时,金属框ab边刚好跨过区域Ⅰ的左边界以速度v向右运动。在τ时刻,ab边运动到距区域Ⅰ的左边界处,金属框的速度近似为零,此时金属框被固定,如图(a)中的虚线框所示。随后在τ~2τ时间内,Ⅰ区磁感应强度线性减小到0,Ⅱ区磁场保持不变;2τ~3τ时间内,Ⅱ区磁感应强度也线性减小到0。求:
(1)t=0时金属框所受的安培力F;
(2)t=1.2τ时穿过金属框的磁通量Φ;
(3)2τ~3τ时间内,金属框中产生的热量Q。
[解析] (1)由题图可知t=0时金属框切割磁感线的感应电动势为E=2B0hv+B0hv=3B0hv
则感应电流大小为I==
所受的安培力为
F=2B0h+B0h=
方向水平向左。
(2)在τ时刻,ab边运动到距区域Ⅰ的左边界处,金属框的速度近似为零,此时金属框被固定,则t=1.2τ时穿过金属框的磁通量为
Φ=1.6B0h·h-B0h·h=。
(3)2τ~3τ时间内,Ⅱ区磁感应强度也线性减小到0,则有E′===
感应电流大小为I′==
则2τ~3τ时间内,金属框中产生的热量为
Q=I′2RΔt=。
[答案] ,方向水平向左 (2)
[典例4] (功率的计算)如图所示,两条相距d的平行金属导轨位于同一水平面内,其右端接一阻值为R的电阻。质量为m的金属杆静置在导轨上,其左侧的矩形匀强磁场区域MNPQ的磁感应强度大小为B、方向竖直向下。当该磁场区域以速度v0匀速地向右扫过金属杆后,金属杆的速度变为v。导轨和金属杆的电阻不计,导轨光滑且足够长,杆在运动过程中始终与导轨垂直且两端与导轨保持良好接触。求:
(1)MN刚扫过金属杆时,杆中感应电流的大小I;
(2)MN刚扫过金属杆时,杆的加速度大小a;
(3)PQ刚要离开金属杆时,感应电流的功率P。
[解析] (1)MN刚扫过金属杆时,金属杆的感应电动势E=Bdv0 ①
回路中的感应电流I= ②
由①②式解得I=。 ③
(2)金属杆所受的安培力F=BId ④
对金属杆由牛顿第二定律得F=ma ⑤
由③④⑤式得a=。 ⑥
(3)金属杆切割磁感线的相对速度
v′=v0-v ⑦
感应电动势E=Bdv′ ⑧
感应电流的电功率P= ⑨
由⑦⑧⑨式得P=。 ⑩
[答案] (1) (2) (3)
1.对于两导体棒在平直的光滑导轨上运动的情况,如果两棒所受的外力之和为零,则考虑应用动量守恒定律处理问题。
2.由BL·Δt=m·Δv、q=·Δt可知,当题目中涉及电荷量或平均电流时,可应用动量定理来解决问题。
考点2 动量观点在电磁感应问题中的应用
[典例5] (动量观点在电磁感应问题中的应用)如图所示,两平行光滑长直金属导轨水平放置,间距为L。abcd区域有匀强磁场,磁感应强度大小为B,方向竖直向上。初始时刻,磁场外的细金属杆M以初速度v0向右运动,磁场内的细金属杆N处于静止状态。两金属杆与导轨接触良好且运动过程中始终与导轨垂直。两杆的质量均为m,在导轨间的电阻均为R,感应电流产生的磁场及导轨的电阻忽略不计。
(1)求M刚进入磁场时受到的安培力F的大小和方向;
(2)若两杆在磁场内未相撞且N出磁场时的速度为,求:
①N在磁场内运动过程中通过回路的电荷量q;
②初始时刻N到ab的最小距离x。
[解析] (1)细金属杆M以初速度v0向右刚进入磁场时,产生的动生电动势为
E=BLv0
感应电流大小为I=
则所受的安培力大小为F=BIL=
由左手定则可知安培力的方向水平向左。
(2)①金属杆N在磁场内运动过程中,设回路中的平均电流为,由动量定理得
BL·Δt=m·-0
且q=·Δt
联立解得q=。
②设两杆在磁场中相对靠近的位移为Δx,有
=
=
整理可得q=
联立解得Δx=
由于两杆未相撞,所以初始时刻N到ab的最小距离为x=Δx=。
[答案] (1) 方向水平向左 (2)① ②
规律总结 两金属杆在平直的光滑导轨上运动,只受到安培力作用,这类问题可以从以下三个观点来分析:
(1)力学观点:通常情况下一个金属杆做加速度逐渐减小的加速运动,而另一个金属杆做加速度逐渐减小的减速运动,最终两金属杆以共同的速度匀速运动。
(2)能量观点:其中一个金属杆动能的减少量等于另一个金属杆动能的增加量与回路中产生的焦耳热之和。
(3)动量观点:如果光滑导轨间距恒定,则两个金属杆所受的安培力大小相等,通常情况下系统的动量守恒。
[典例6] (动量定理在电磁感应现象中的应用)(2024·浙江1月选考)如图1所示,扫描隧道显微镜减振装置由绝缘减振平台和磁阻尼减振器组成。平台通过三根关于O′O″轴对称分布的相同轻杆悬挂在轻质弹簧的下端O,弹簧上端固定悬挂在O′点,三个相同的关于O′O″轴对称放置的减振器位于平台下方。如图2所示,每个减振器由通过绝缘轻杆固定在平台下表面的线圈和固定在桌面上能产生辐向磁场的铁磁体组成,辐向磁场分布关于线圈中心竖直轴对称,线圈所在处磁感应强度大小均为B。处于静止状态的平台受到外界微小扰动,线圈在磁场中做竖直方向的阻尼运动,其位移随时间变化的图
像如图3所示。已知t=0时速度为v0,方向向下,t1、t2时刻的振幅分别为A1、A2。平台和三个线圈的总质量为m,弹簧的劲度系数为k,每个线圈半径为r、电阻为R。当弹簧形变量为Δx时,其弹性势能为k(Δx)2。不计空气阻力,求:
(1)平台静止时弹簧的伸长量Δx;
(2)t=0时,每个线圈所受到安培力F的大小;
(3)在0~t1时间内,每个线圈产生的焦耳热Q;
(4)在t1~t2时间内,弹簧弹力冲量I弹的大小。
[解析] (1)平台静止时,三个线圈均不切割磁感线,线圈中不产生感应电流,线圈不受到安培力作用,O点受力平衡,因此由胡克定律可知此时弹簧的伸长量Δx=。
(2)在t=0时速度为v0,设每个线圈的周长为L,由法拉第电磁感应定律结合欧姆定律可得线圈中产生的感应电流
I====
每个线圈所受到安培力F的大小
F=BIL=。
(3)在0~t1时间内,由能量守恒定律得
Q′+mgA1=+k(Δx)2-k(Δx-A1)2
在0~t1时间内,振动时能量的减少转化为线圈的焦耳热,可知每个线圈产生的焦耳热
Q=Q′=。
(4)取向上为正方向,全程由动量定理可得
I弹+IA-mg(t2-t1)=0
IA=3×2πrB·Δq
Δq=
联立解得弹簧弹力冲量I弹的大小为
I弹=mg(t2-t1)-。
[答案] (1) (2) (4)mg(t2-t1)-
【典例6 教用·备选题】 (动量定理在电磁感应现象中的应用)(2025·无锡调研)两足够长且不计电阻的光滑金属轨道如图甲所示放置,间距为d=1 m,在左端弧形轨道部分高h=1.25 m 处放置一金属杆a,弧形轨道与平直轨道的连接处光滑无摩擦,在平直轨道右端放置另一金属杆b,杆a、b的电阻分别为 Ra=2 Ω、Rb=
5 Ω,在平直轨道区域有竖直向上的匀强磁场,磁感应强度B=
2 T。 现杆b以初速度大小v0=5 m/s 开始向左滑动,同时由静止释放杆a,杆a由静止滑到水平轨道的过程中,通过杆b的平均电流为0.3 A;从a下滑到水平轨道时开始计时,a、b运动的速度—时间图像如图乙所示(以a运动方向为正方向),其中ma=2 kg,mb=1 kg,g取10 m/s2,求:
(1)杆a在弧形轨道上运动的时间;
(2)杆a在水平轨道上运动过程中通过其截面的电荷量;
(3)在整个运动过程中杆b产生的焦耳热。
[解析] (1)设杆a由静止滑至弧形轨道与平直轨道连接处时杆b的速度大小为vb0,对杆b运用动量定理,有Bd·Δt=-mb(vb0-v0)
其中vb0=2 m/s
代入数据解得Δt=5 s。
(2)对杆a由静止下滑到平直导轨上的过程中,由机械能守恒定律有magh=
解得va==5 m/s
设最后a、b两杆共同的速度为v′,由动量守恒定律得mava-mbvb0=(ma+mb)v′
代入数据解得v′= m/s
杆a动量的变化量等于它所受安培力的冲量,设杆a的速度从va到v′的运动时间为Δt′,则由动量定理可得-BdI·Δt′=ma(v′-va)
而q=I·Δt′
代入数据得q= C。
(3)由能量守恒定律可知杆a、b中产生的焦耳热为
Q=-(mb+ma)v′2= J
杆b中产生的焦耳热为Q′=Q= J。
[答案] (1)5 s (2) C (3) J
【典例6 教用·备选题】 (动量定理在电磁感应现象中的应用)如图所示,与水平面夹角为θ的绝缘斜面上固定有光滑U形金属导轨。质量为m、电阻不可忽略的导体杆MN沿导轨向下运动,以大小为v的速度进入方向垂直于导轨平面向下的匀强磁场区域,在磁场中运动一段时间t后,速度大小变为2v。运动过程中杆与导轨垂直并接触良好,导轨的电阻忽略不计,重力加速度为g。杆在磁场中运动的此段时间内( )
A.流过杆的感应电流方向为从N到M
B.杆沿导轨下滑的距离为vt
C.流过杆的感应电流的平均电功率等于重力的平均功率
D.杆所受安培力的冲量大小为mgt sin θ-mv
√
D [根据右手定则,判断知流过杆的感应电流方向为从M到N,故A错误;依题意,设杆切割磁感线的有效长度为L,电阻为R,杆在磁场中运动的此段时间内,杆受到重力、导轨支持力及沿导轨向上的安培力作用,根据牛顿第二定律可得mg sin θ-F安=ma,F安=BIL,I=,联立可得杆的加速度a=g sin θ-,可知,杆在磁场中运动的此段时间内做加速度逐渐减小的加速运动,若杆做匀加速直线运动,则杆运动的距离为s=·t=vt,根据 v-t 图像
围成的面积表示位移,可知杆在时间t内速度由v达到2v,杆真实运动的距离大于匀加速情况运动的距离,即大于vt,故B错误;由于在磁场中运动的此段时间内,杆做加速度逐渐减小的加速运动,杆的动能增大,由动能定理可知,重力对杆所做的功大于杆克服安培力所做的功,根据=可得安培力的平均功率小于重力的平均功率,即流过杆感应电流的平均电功率小于重力的平均功率,故C错误;杆在磁场中运动的此段时间内,根据动量定理,可得mgt sin θ-I安=m·2v-mv,得杆所受安培力的冲量大小为I安=mgt sin θ-mv,故D正确。故选D。]
[典例7] (动量守恒定律在电磁感应中的应用)如图所示,在水平面内固定有两根相互平行的无限长光滑金属导轨,其间距为L,电阻不计。在虚线l1的左侧存在竖直向上的匀强磁场,在虚线l2的右侧存在竖直向下的匀强磁场,两部分磁场的磁感应强度大小均为B。ad、bc两根电阻均为R的金属棒与导轨垂直,分别位于两磁场中,现突然给ad棒一个水平向左的初速度v0,在两棒达到稳定的过程中,下列说法正确的是( )
A.两金属棒组成的系统的动量守恒
B.两金属棒组成的系统的动量不守恒
C.ad棒克服安培力做功的功率等于ad棒的发热功率
D.ad棒克服安培力做功的功率等于安培力对bc棒做功的功率与bc棒发热功率之和
√
B [开始时,ad棒以初速度v0切割磁感线,产生感应电动势,在回路中产生顺时针方向(俯视)的感应电流,ad棒因受到向右的安培力而减速,bc棒受到向右的安培力而向右加速;当两棒的速度大小相等,即两棒因切割磁感线而产生的感应电动势相等时,回路中没有感应电流,两棒各自做匀速直线运动;由于两棒所受的安培力都向右,两金属棒组成的系统所受合外力不为零,所以该系统的动量不守恒,A错误,B正确;根据能量守恒定律可知,ad棒动能的减小量等于回路中产生的热量和bc棒动能的增加量,由动能定理可知,ad棒动能的减小量等于ad棒克服安培力做的功,bc棒动能的增加量等于安培力对bc棒做的功,所以ad棒克服安培力做功的功率等于安培力对bc棒做功的功率与两棒总发热功率之和,C、D错误。]
[典例8] (三大观点的综合应用)(2024·湖北卷)如图所示,两足够长平行金属直导轨MN、PQ的间距为L,固定在同一水平面内,直导轨在左端M、P点分别与两条竖直固定、半径为L的圆弧导轨相切。MP连线与直导轨垂直,其左侧无磁场,右侧存在磁感应强度大小为B、方向竖直向下的匀强磁场。长为L、质量为m、电阻为R的金属棒ab跨放在两圆弧导轨的最高点。质量为2m、电阻为6R的均匀金属丝制成一个半径为L的圆环,水平放置在两直导轨上,其圆心到两直导轨的距离相等。忽略导轨的电阻、所有摩擦以及金属环的可能形变,金属棒、金属环均与导轨始终接触良好,重力加速度大小为g。现将金属棒ab由静止释放,求:
(1)ab刚越过MP时产生的感应电动势大小;
(2)金属环刚开始运动时的加速度大小;
(3)为使ab在整个运动过程中不与金属环接触,金属环圆心初始位置到MP的最小距离。
[解析] (1)设ab棒刚越过MP时速度大小为v1,产生的电动势大小为E1,对ab在圆弧导轨上运动的过程,由机械能守恒定律有
mgL=
ab刚越过MP时,由法拉第电磁感应定律得
E1=BLv1
联立解得E1=BL。
(2)经分析知金属环在导轨外的两段电阻被短路,由几何关系可知导轨之间两段金属环的电阻均为R,它们在电路中并联后的总电阻Rc=
设电路中初始的干路电流为I1,由闭合电路欧姆定律有I1=
经分析知整个金属环在运动过程中可视为长度为L、电阻为Rc的金属棒,设金属环刚开始运动时所受的安培力大小为F1、加速度大小为a,则
F1=I1LB
由牛顿第二定律得F1=2ma
联立解得a=。
(3)经分析,ab进入磁场后,ab和金属环组成的系统动量守恒,设两者共速时的速度大小为v2,由动量守恒定律得mv1=(m+2m)v2
设在极短时间Δt内,ab与金属环圆心的距离减少量为Δx,金属环所受安培力大小为F,流过ab的电流为I,整个电路的电动势为E,对金属环,由动量定理得=2mv2-0
又F=ILB
由闭合电路欧姆定律得I=
设金属环圆心初始位置到MP的最小距离为s,若ab与金属环共速时,两者恰好接触,金属环圆心初始位置到MP的距离最小,对ab进入磁场到两者共速的过程,由法拉第电磁感应定律有
E=BL
又s=L+
联立解得s=+L。
[答案] (1)BL (2)
(3)+L
【典例8 教用·备选题】(三大观点的综合应用)如图,两根足够长的光滑金属直导轨平行放置,导轨间距为L,两导轨及其所构成的平面均与水平面成θ角,整个装置处于垂直于导轨平面斜向上的匀强磁场中,磁感应强度大小为B。现将质量均为m的金属棒a、b垂直导轨放置,每根金属棒接入导轨之间的电阻均为R。运动过程中金属棒与导轨始终垂直且接触良好,金属棒始终未滑出导轨,导轨电阻忽略不计,重力加速度为g。
(1)先保持棒b静止,将棒a由静止释放,
求棒a匀速运动时的速度大小v0;
(2)在(1)问中,当棒a匀速运动时,再将棒b由静止释放,求释放瞬间棒b的加速度大小a;
(3)在(2)问中,从棒b释放瞬间开始计时,经过时间t0,两棒恰好达到相同的速度v,求速度v的大小,以及时间t0内棒a相对于棒b运动的距离Δx。
[解析] (1)金属棒a在运动过程中重力沿斜面的分力和棒a受到的安培力相等时做匀速运动,由法拉第电磁感应定律可得E=BLv0
由闭合电路欧姆定律及安培力公式可得
I=,F=BIL
由棒a受力平衡可得mg sin θ=BIL
联立解得v0=。
(2)由右手定则可知金属棒b中电流向里,由左手定则可知棒b受到沿斜面向下的安培力,此时电路中电流不变,则对棒b由牛顿第二定律可得mg sin θ+BIL=ma
解得a=2g sin θ。
(3)释放棒b后棒a受到沿斜面向上的安培力,在到达共速的过程对棒a由动量定理得
mg sin θt0-BLt0=mv-mv0
棒b受到向下的安培力,对棒b由动量定理得
mg sin θt0+BLt0=mv
联立解得v=g sin θt0+
此过程流过棒b的电荷量为q,则有q=t0
由法拉第电磁感应定律可得
==
联立可得Δx==。
[答案] (1) (2)2g sin θ
(3)g sin θt0+
电磁感应中常见的图像问题
考点3 电磁感应中的图像问题
图像类型 (1)随时间变化的图像,如B-t图像、Φ-t图像、E-t图像、I-t图像;
(2)随位移变化的图像,如E-x图像、I-x图像
(先看坐标轴:弄清哪个物理量随哪个物理量变化)
问题类型 (1)由给定的电磁感应过程选出或画出正确的图像(画图像);
(2)由给定的有关图像分析电磁感应过程,求解相应的物理量(用图像)
应用 知识 四个规律 左手定则、安培定则、右手定则、楞次定律
六类公式 (1)平均电动势E=n
(2)平动切割电动势E=Blv
(3)转动切割电动势E=Bl2ω
(4)闭合电路欧姆定律I=
(5)安培力F=BIl
(6)牛顿运动定律的相关公式等
[典例9] (根据电磁感应过程选择图像)空间中存在如图所示的磁场,Ⅰ、Ⅱ区域的宽度均为2R,磁感应强度大小均为B(Ⅰ区域磁场方向垂直纸面向里,Ⅱ区域磁场方向垂直纸面向外),半径为R的圆形导线框在外力作用下以速度v匀速通过磁场区域,设任意时刻导线框中电流为I(逆时针为正),导线框所受安培力为F(向左为正),从导线框刚进入Ⅰ区域开始将向右运动的位移记为x,则下列图像正确的是( )
A B
C D
√
D [当导线框在磁场Ⅰ区域向右运动过程中,设导线框切割磁感线的等效长度为l,则有(R-x)2+=R2,整理得l=2, 则导线框产生的感应电动势为E=Blv,感应电流为I==,可知电流与位移不成线性关系,B错误;当导线框圆心运动到Ⅰ、Ⅱ区域的边界时,此时产生的感应电流大小为I′==,即导线框在x=3R时的电流大
小为x=R时的两倍,方向沿着顺时针方向,A错误;通过分析可知,除了x=2R、x=4R、x=6R三个特殊位置,电流为0,受力为0,在0【典例9 教用·备选题】 (根据电磁感应过程选择图像)如图所示,两根光滑平行金属长导轨MN、PQ水平固定放置,导轨间存在竖直向上的匀强磁场,两根完全相同的金属棒ab、cd垂直放置在导轨上,两金属棒的长度恰好等于金属导轨的间距,t=0时刻对金属棒cd施加一个水平向右的恒力F,此后两金属棒由静止开始运动,金属棒在运动过程中始终与导轨接触良好,两金属棒的速度大小分别记为va、vc,加速度大小分别记为aa、ac,金属棒cd两端电压记为Ucd,闭合回路消耗的电功率记为P,电路中除金属棒以外的电阻均不计,下列关系图像错误的是( )
A B
C D
√
B [金属棒cd在恒力F作用下由静止开始加速,此时金属棒ab、cd的加速度aa=0、ac=,之后回路中出现感应电流,金属棒cd受到的安培力与恒力F反向,金属棒cd的加速度减小,金属棒ab在安培力的作用下开始加速,金属棒cd与金属棒ab的速度差逐渐增大,回路中的电动势逐渐增大,安培力F安=,逐渐增大,金属棒ab加速度增大,当aa=ac时,vc-va不再变化,回路中的电流不再变化,但是两金属棒的速度仍在增大,故A正确,与题意不符,B
错误,与题意相符;设两金属棒电阻均为R,系统达到稳定之前,Ucd=BLva+IR,Ucd随时间逐渐增大,系统达到稳定后,因回路中电流不变,则Ucd=BLvc-IR,Ucd随着vc的增加而均匀增加,故C正确,与题意不符;闭合回路消耗的电功率P=2I2R,在开始阶段随回路中电流的增大,电功率逐渐增大,当系统稳定后回路中电流不变,电功率不再变化,故D正确,与题意不符。本题选错误的,故选B。]
方法技巧 电磁感应中图像选择类的两个常用方法
排除法 定性地分析电磁感应过程中物理量的变化趋势(增大还是减小)、变化快慢(均匀变化还是非均匀变化),特别是分析物理量的正负,以排除错误的选项。
函数法 根据题目所给条件定量地写出两个物理量之间的函数关系,然后由函数关系对图像进行分析和判断。
[典例10] (根据图像分析判断电磁感应过程)(2024·江苏南京一模)世界首个电磁驱动地面超高速试验设施——“电磁橇”在我国济南阶段性建成并成功运行,电磁橇可以将吨级及以上物体最高加速到 1 030 公里的时速,创造了大质量超高速电磁推进技术的世界最高速度纪录。电磁橇运用了电磁弹射的原理,图甲是一种电磁弹射装置的原理图,开关S先拨向1,直流电源向电容器充电,待电容器充好电后在t=0时刻将开关S拨向2,发射线圈被弹射出去,如图乙所示,电路中电流在t=t0时刻达到峰值后减小。假设发射线圈由粗细均匀的同种金属导线绕制而成,发射导管材质绝缘,管内光滑,下列说法正确的是( )
A.在0~t0时间内,发射线圈的加速度不断增大
B.在0~t0时间内,发射线圈中的电流不断增大
C.增加发射线圈的匝数,发射线圈加速度不变
D.发射导管越长,发射线圈的出射速度越大
√
C [在0~t0时间内,驱动线圈中的电流逐渐变大,但是电流的变化率逐渐减小,则穿过发射线圈的磁通量的变化率逐渐减小,则发射线圈中产生的电流不断减小,在t=t0时刻发射线圈中的电流减小为0,根据F=BIL可知,发射线圈所受的安培力不是不断增大,则发射线圈的加速度不是不断增大,故A、B错误;根据E=n,设单匝线圈的电阻为r0,质量为m0,线圈的半径为r,则电流为I==,安培力为F=nBI·2πr,加速度为a===,则增加发射线圈的匝数,发射线圈加速度不变,故C正确;对发射线圈根据动量定理可得F安t=mv,而F安t=nBLt=nBL, 则安培力的冲量以及发射线圈的出射速度与发射导管的长度无关,故D错误。故选C。]
【典例10 教用·备选题】 (根据图像分析判断电磁感应过程)(2024·锡山模拟)如图甲所示,在水平面上固定一个匝数为10匝的等边三角形金属线框,总电阻为 3 Ω, 边长为0.4 m。金属框处于两个半径为0.1 m的圆形匀强磁场中,顶点A恰好位于左边圆的圆心,BC边的中点恰好与右边圆的圆心重合。左边磁场方向垂直纸面向外,右边磁场方向垂直纸面向里,磁感应强度的变化规律如图乙所示,磁场方向垂直纸面向里为正方向,则下列说法中正确的是(π取3)( )
A.线框中感应电流的方向是顺时针方向
B.t=0.4 s时,穿过线框的磁通量为0.005 Wb
C.经过t=0.4 s,线框中产生的热量为0.3 J
D.前0.4 s内流过线框某截面的电荷量为 0.4 C
√
C [根据楞次定律和安培定则,线框中感应电流的方向是逆时针方向,A错误;0.4 s时穿过线框的磁通量Φ=Φ1-Φ2=πr2·B1-πr2·B2=0.055 Wb,B错误;由题图乙知==10 T/s, 根据法拉第电磁感应定律,感应电动势E=n=n·πr2·=
1.5 V,感应电流I==0.5 A,0.4 s内线框中产生的热量Q=I2Rt=0.3 J,C正确;前 0.4 s 内流过线框某截面的电荷量q=It=0.2 C,D错误。]
【典例10 教用·备选题】 (根据图像分析判断电磁感应过程)如图(a)所示,在同一平面内固定有一长直导线PQ和一导线框R,R在PQ的右侧。导线PQ中通有正弦交流电i,i的变化如图(b)所示,规定从Q到P为电流正方向。导线框R中的感应电动势( )
A.在t=时最大
B.在t=时改变方向
C.在t=时最大,且沿顺时针方向
D.在t=T时最大,且沿顺时针方向
√
C [因通电导线的磁感应强度大小正比于电流的大小,故导线框R中磁感应强度与时间的变化关系类似于题图(b),感应电动势正比于磁感应强度的变化率,即题图(b)中的切线斜率,斜率的正负反映感应电动势的方向,斜率的绝对值反映感应电动势的大小。由题图(b)可知,电流为零时,感应电动势最大,电流最大时,感应电动势改变方向,A、B错误;再由楞次定律可判断在一个周期内,~时间内感应电动势的方向沿顺时针,时刻最大,C正确;其余时间段感应电动势沿逆时针方向,D错误。]
[典例11] (电磁感应中图像的转换)(2024·江苏无锡一模)如图1所示,绝缘细线的下端悬挂着一金属材料做成的空心心形挂件,该挂件所在空间水平直线MN下方存在匀强磁场,初始时刻磁场方向垂直挂件平面向里,且大小随时间的变化如图2所示。若某段时间内挂件处于静止状态,则该段时间内挂件中产生的感应电流的大小i、通过线框某一横截面的电荷量Q、挂件所受安培力F的大小、细线拉力T的大小随时间t变化的规律不可能是( )
A B
C D
√
D [根据法拉第电磁感应定律可得感应电动势为E==S有=kS有,可知感应电动势保持不变,设空心心形挂件的电阻为R,则电流为I=,可知挂件中产生的感应电流保持不变;根据Q=It可知Q-t图像为过原点的倾斜直线;根据F=BIL有知,由于B随时间均匀减小,则安培力F随时间均匀减小,故A、B、C正确,不满足题意要求。穿过空心心形挂件的磁通量向里减小,根据楞次定律可知,挂件中感应电流方向为顺时针方向,根据左手定则可知,安培力方向竖直向下,根据受力平衡可得T=mg+F,由于安培力F随时间均匀减小,则细线拉力T随时间均匀减小,但拉力T不会减小到0,故D错误,满足题意要求。故选D。]
【典例11 教用·备选题】 (电磁感应中图像的转换)有一磁场方向竖直向下,磁感应强度B随时间t的变化关系如图甲所示。现有如图乙所示的直角三角形导线框abc水平放置,放在匀强磁场中保持静止不动,t=0时刻,磁感应强度B的方向垂直纸面向里,设产生的感应电流i顺时针方向为正方向,竖直边ab所受安培力F的方向水平向左为正方向。则下面关于F和i随时间t变化的图像正确的是
( )
A B
C D
√
A [在0~3 s时间内,磁感应强度随时间线性变化,由法拉第电磁感应定律可知,感应电动势恒定,回路中感应电流恒定, 同时由F=BIL知道,电流恒定,安培力与磁感应强度成正比, 又由楞次定律判断出回路中感应电流的方向应为顺时针方向,即正方向, 故D错误;在3~4 s时间内,磁感应强度恒定,感应电动势等于零,感应电流为零,安培力等于零,故B、C错误;4~7 s时间内,磁感应强度随时间线性变化,由法拉第电磁感应定律可知,感应电动势恒定,回路中感应电流恒定,安培力与磁感应强度成正比,故A正确。]
规律总结 “四明确、一理解”巧解图像问题
题组一 电磁感应中的能量问题
1.如图所示,两条电阻不计的平行光滑导轨竖直放置在垂直纸面向里的匀强磁场内,已知磁感应强度B=0.5 T,导体棒ab、cd的长度均为 0.2 m, 电阻均为0.1 Ω,重力均为 0.1 N。 现用力向上拉动导体棒ab,使之匀速上升(导体棒ab、cd与导轨接触良好),此时cd静止不动。则在ab上升时,下列说法正确的是( )
1
题号
2
3
4
5
6
7
8
9
10
11
课时分层作业(三十一) 电磁感应中动量能量问题和图像问题
A.ab受到的拉力大小为2 N
B.ab向上运动的速度为2 m/s
C.在2 s内,拉力做功,有0.5 J的机械能转化为电能
D.在2 s内,拉力做功为0.6 J
1
题号
2
3
4
5
6
7
8
9
10
11
√
B [对导体棒cd分析:mg=BIl=,代入数据解得 v=2 m/s,B正确;对导体棒ab分析:F=mg+BIl=0.2 N,A错误;在2 s内拉力做功转化为ab棒的重力势能和电路中的电能,电能等于克服安培力做的功,即W电=F安vt==0.4 J,C错误;在2 s内拉力做的功为W拉=Fvt=0.8 J,D错误。]
1
题号
2
3
4
5
6
7
8
9
10
11
2.如图所示,竖直平面内在A、D两点各固定一颗光滑钉子,一个由细软导线制成的闭合导线框挂在两颗钉子上,匀强磁场的磁感应强度为B,导线框的电阻为r,圆的半径为R。重物通过绝缘动滑轮挂在导线框上。从t=0时刻开始,将导线上的C点绕圆心O以恒定角速度ω从A点沿圆弧移动到D点,导线始终绷紧。
此过程导线中( )
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
A.张力保持不变
B.感应电流的方向先顺时针后逆时针
C.感应电流i随时间t的变化关系为i=
D.产生的电热为
√
D [对滑轮分析可知,两边绳子拉力总是相等的,则两边绳子与竖直方向的夹角总相等,随着C点沿圆弧从A点移到D点,AC段与CD段绳子长度之和先增加后减小,则AE段与ED段绳子长度之和先减小后增加,AE段绳子与ED段绳子的夹角先增加后减小,由2T cos α=mg可知,绳子的张力先增加后减小,故A错误;设C点转过的角度为θ=ωt,根据几何知识可得,线框上的三角形的面积为S=
1
题号
2
3
4
5
6
7
8
9
10
11
·2R·R sin θ=R2sin θ,磁通量为Φ=BS=BR2sin θ,因θ角从0°到180°,则导线框中的磁通量先增大后减小,根据楞次定律可知,感应电流先沿逆时针方向,后沿顺时针方向,故B错误;根据法拉第电磁感应定律E=可知,导线框中感应电动势随时间t的变化关系为e=ωBR2cos ωt,感应电流随时间t的变化关系为i=,故C错误;导线框中感应电动势的有效值为E=,故导线框中产生的电热为Q==,故D正确。故选D。]
1
题号
2
3
4
5
6
7
8
9
10
11
3.如图所示,水平面上固定着两根相距L且电阻不计的足够长的光滑金属导轨,导轨处于方向竖直向下、磁感应强度为B的匀强磁场中,铜棒a、b的长度均等于两导轨的间距、电阻均为R、质量均为m,铜棒平行地静止在导轨上且与导轨接触良好,现给铜棒a一个平行导轨向右的瞬时冲量I,关于此后的过程,下列说法正确的是
( )
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
A.回路中的最大电流为
B.铜棒b的最大加速度为
C.铜棒b获得的最大速度为
D.回路中产生的总焦耳热为
√
B [由题意知a获得冲量I时速度最大,即va=,此后a在安培力作用下做减速运动,b在安培力作用下做加速运动,回路中产生的电动势E=BL(va-vb),可知a刚获得冲量时回路中产生的感应电流最大,即Im==,故A错误;开始时b所受安培力最大,即Fm=BImL=,则b的最大加速度am= =,故B正确;由题意知,a做减速运动,b做加速运动,当a、b速度相等时,两棒同时向右做匀速直线运动,根据动量守恒定律可知,I=2mvab,即vab=,此速度亦为b的最大速度,故C错误;根据系统能量守恒,则有=+Q,即Q=,故D错误。]
1
题号
2
3
4
5
6
7
8
9
10
11
题组二 动量观点在电磁感应问题中的应用
4.如图所示,在光滑的水平面上宽度为L的区域内,有垂直水平面向里的匀强磁场。现有一个边长为a(aA.大于 B.等于
C.小于 D.以上均有可能
1
题号
2
3
4
5
6
7
8
9
10
11
√
B [通过线圈横截面的电荷量为q=Δt=
t,则-Baq=mv-mv0,-Baq=-mv,解得v=。故选B。]
1
题号
2
3
4
5
6
7
8
9
10
11
5.如图甲所示,水平面上有两根足够长的光滑平行金属导轨MN和PQ,两导轨间距为l,电阻均可忽略不计。在M和P之间接有阻值为R的定值电阻,导体杆ab质量为m、电阻为r,并与导轨接触良好。整个装置处于方向竖直向上、磁感应强度大小为B的匀强磁场中。现给杆ab一个初速度v0,使杆向右运动。则( )
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
A.当杆ab刚具有初速度v0时,杆ab两端的电压U=,且b点电势高于a点电势
B.通过电阻R的电流I随时间t的变化率的绝对值逐渐增大
C.若将M和P之间的电阻R改为接一电容为C的电容器,如图乙所示,同样给杆ab一个初速度v0,使杆向右运动,则杆ab稳定后的速度为v=
D.在C选项中,杆稳定后b点电势高于a点电势
√
C [当杆ab刚具有初速度v0时,其切割磁感线产生的感应电动势E=Blv0,杆ab两端的电压U==,根据右手定则知,感应电流的方向为b到a,杆ab相当于电源,a相当于电源的正极,则a点电势高于b点电势,A错误;通过电阻R的电流I=,由于杆ab速度减小,则电流减小,安培力减小,所以杆ab做加速度逐渐减小的减速运动,速度v随时间t的变化率的绝对值逐渐减小,则通过电阻R的电流I随时间t的变化率的绝对值逐渐减小,B错误;当杆ab以初速度v0开始切割磁感线时,电路开始给电容器充电,有电流通过杆ab,
1
题号
2
3
4
5
6
7
8
9
10
11
杆在安培力的作用下做减速运动,随着速度减小,安培力减小,加速度也减小,当电容器两端电压与感应电动势相等时,充电结束,杆以恒定的速度做匀速直线运动,电容器两端的电压U=Blv,而q=CU,对杆ab,根据动量定理得-Bl·Δt=mv-mv0,联立可得v=,C正确;杆稳定后,电容器不再充电,回路中没有电流,根据右手定则知,a点的电势高于b点电势,D错误。]
1
题号
2
3
4
5
6
7
8
9
10
11
题组三 电磁感应中的图像问题
6.(2025·江苏徐州模拟)如图甲所示,有一足够长的水平、平行金属轨道,轨道间距为L=1 m,整个轨道位于竖直向上的匀强磁场中,轨道电阻可忽略不计。轨道左端连接一阻值R=0.2 Ω的定值电阻,有一阻值r=0.2 Ω(导轨间部分)、质量m=1×10-2 kg的导体棒放在轨道上,导体棒长度大于L,导体棒与轨道间的动摩擦因数μ=0.2。现有一大小为6×10-2 N、垂直导体棒的水平恒力F作用在导体棒上,使其从静止开始运动。导体棒运动过程中,0~t时间通过电阻的电荷量q与时间t的关系如图乙所示,其中0~0.3 s为曲线,0.3~0.4 s为直线,已知导体棒始终与轨道垂直,重力加速度取g=10 m/s2, 下列说法正确的是( )
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
A.导体棒的最大速度为0.2 m/s
B.磁感应强度大小为0.4 T
C.0~0.3 s时间内,电阻上产生的热量为2.4×10-3 J
D.0~0.3 s时间内,导体棒的位移大小为8×10-2 m
√
D [0.3~0.4 s时间内,电荷量随时间均匀增加,电流稳定,即导体棒开始做匀速直线运动,达到最大运动速度,此时I===0.2 A,F=μmg+BIL,联立解得B==0.2 T,vm=0.4 m/s, A、B错误;0~0.3 s时间内,导体棒在外力作用下做加速度减小的加速运动,对导体棒由动量定理得Ft1-μmgt1-t1=mvm-0,即Ft1-μmgt1-=mvm-0,解得x=8×10-2 m,由动能定理得=-0,而Q总=,QR=Q总,联立解得QR=1.2×10-3 J,C错误,D正确。故选D。]
1
题号
2
3
4
5
6
7
8
9
10
11
7.(2024·江苏南京一模)如图所示,两根足够长的平行光滑金属导轨电阻不计,水平固定在竖直向上的匀强磁场中,导轨上垂直静置两根质量与电阻都相同的导体棒ab、cd。给ab棒平行于导轨的初速度并开始计时,棒ab、cd中产生的感应电动势eab、ecd、回路中的感应电流i、导轨间的电压u与时间t的关系图像中,可能正确的是
( )
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
A B
C D
√
D [设磁感应强度为B,两导体棒的质量均为m、接入电路的长度均为d、电阻均为R,导体棒ab的初速度为v0,某时刻t,导体棒ab、cd的速度分别为v1、v2,回路中的感应电流为i,由法拉第电磁感应定律有eab=Bdv1,ebc=Bdv2,i=,两导体棒受到的安培力大小为F=Bdi,方向与棒ab运动方向相反,与棒cd运动方向相同,棒ab减速、棒cd加速,v1减小、v2增大,(v1-v2)减小,电流i减小,
1
题号
2
3
4
5
6
7
8
9
10
11
F=Bdi减小,棒运动的加速度减小,即棒ab做初速为v0、加速度逐渐减小的减速运动,由eab=Bdv1可知eab减小得越来越慢,最终趋于,故A错误;棒cd做初速为零、加速度逐渐减小的加速运动,由ecd=Bdv2可知ecd由零开始增加得越来越慢,最终趋于恒定,故B错误;依题意,(v1-v2)越来越小,最终趋近于零,故i趋近于零,故C错误;两导轨间的电压u=eab-iR,对两棒由动量守恒定律有mv0=mv1+mv2,联立解得u=,可知u恒定,故D正确。故选D。]
1
题号
2
3
4
5
6
7
8
9
10
11
8.如图甲所示,在倾斜角为θ的光滑斜面内分布着垂直于斜面的匀强磁场,以垂直于斜面向上为磁感应强度正方向,其磁感应强度B随时间变化的规律如图乙所示。质量为m的矩形金属框从t=0时刻由静止释放,t3时刻的速度为v,移动的距离为L,重力加速度为g。在金属框下滑的过程中,下列说法正确的是( )
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
A.t1~t3时间内金属框中的电流方向先顺时针再逆时针方向
B.0~t3时间内金属框做匀加速直线运动
C.0~t3时间内金属框做加速度逐渐减小的直线运动
D.0~t3时间内金属框中产生的焦耳热为mgL sin θ-mv2
√
B [t1~t3时间内穿过金属框的磁通量先垂直于斜面向上减小,后垂直于斜面向下增大,根据楞次定律可知,金属框中的电流方向不变,A错误;0~t3时间内,金属框的ab边与cd边所受安培力等大反向,金属框所受安培力为零,则所受的合力沿斜面向下,大小为mg sin θ,做匀加速直线运动,B正确,C错误;0~t3时间内,金属框所受的安培力为零,金属框的机械能守恒,有mgL sin θ=mv2,而金属框中产生的焦耳热不为零,故金属框中产生的焦耳热不等于mgL sin θ-mv2,D错误。]
1
题号
2
3
4
5
6
7
8
9
10
11
9.(2024·江西卷节选)如图所示,绝缘水平面上固定一光滑平行金属导轨,导轨左右两端分别与两粗糙的倾斜平行金属导轨平滑连接,两侧导轨倾角分别为θ1、θ2,导轨间距均为l=2 m,水平导轨所在区域存在竖直向上的匀强磁场,磁感应强度大小B=0.5 T。 现有两均匀金属细杆甲和乙,质量分别为m1=6 kg和m2=2 kg,接入导轨的电阻均为R=1 Ω。 左、右两侧倾斜导轨与两棒的动摩擦因数分别为μ1=、μ2=。初始时刻,乙静止在水平导轨上,与水平导轨左端P1P2的距离为d,甲从左侧倾斜导轨高度h=4 m的位置静止滑下。水平导轨足够长,两棒运动过程中始终与导轨接触良好且保持垂直。若两棒发生碰撞,则为完全非弹性碰撞。不计空气阻力和导轨的电阻。(g取10 m/s2,sin θ1=0.6,sin θ2=0.8)
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
(1)求甲刚进入磁场时乙的加速度大小和方向;
(2)为使乙第一次到达水平导轨右端Q1Q2之前甲和乙不相撞,求d的最小值。
[解析] (1)对甲从静止运动至水平导轨的过程,根据动能定理有
m1gh-μ1m1g cos θ1·=-0
甲刚进入磁场时,由法拉第电磁感应定律有
E0=Blv0
则根据欧姆定律可知此时回路中的感应电流为
I0=
根据楞次定律可知,回路中的感应电流沿逆时针方向(俯视),结合左手定则可知,乙所受安培力方向水平向右,由牛顿第二定律有BI0l=m2a乙0
代入数据有a乙0=2 m/s2,方向水平向右。
1
题号
2
3
4
5
6
7
8
9
10
11
(2)甲和乙在磁场中运动的过程中,系统不受外力作用,则系统动量守恒,若两者共速时恰不相碰,则有
m1v0=(m1+m2)v共
对乙根据动量定理有Blt=m2v共-0
其中t=q=
联立解得dmin=Δx=24 m。
1
题号
2
3
4
5
6
7
8
9
10
11
[答案] (1)2 m/s2,方向水平向右 (2)24 m
10.如图所示,水平桌面上固定一光滑U形金属导轨,其平行部分的间距为l,导轨的最右端与桌子右边缘对齐,导轨的电阻忽略不计。导轨所在区域有方向竖直向上的匀强磁场,磁感应强度大小为B。一质量为m、电阻为R、长度也为l的金属棒P静止在导轨上。导轨上质量为3m的绝缘棒Q位于P的左侧,以大小为v0的速度向P运动并与P发生弹性碰撞,碰撞时间很短。碰撞一次后,P和Q先后从导轨的最右端滑出导轨,并落在地面上同一地点。P在导轨上运动时,两端与导轨接触良好,P与Q始终平行。不计空气阻力。求:
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
(1)金属棒P滑出导轨时的速度大小;
(2)金属棒P在导轨上运动过程中产生的热量;
(3)与P碰撞后,绝缘棒Q在导轨上运动的时间。
[解析] (1)由于绝缘棒Q与金属棒P发生弹性碰撞,根据动量守恒和能量守恒定律可得
3mv0=3mvQ+mvP
=
联立解得vP=v0,vQ=v0
由题知,碰撞一次后,P和Q先后从导轨的最右端滑出导轨,并落在地面上同一地点,则金属棒P滑出导轨时的速度大小等于绝缘棒Q滑出导轨时的速度大小,即v′P=vQ=v0。
1
题号
2
3
4
5
6
7
8
9
10
11
(2)根据能量守恒定律有=+Q
解得Q=。
(3)P、Q碰撞后,对金属棒P分析,根据动量定理得-BlΔt=mv′P-mvP
又q====
联立可得x=
由于Q为绝缘棒,无电流通过,不受安培力作用,做匀速直线运动,故Q运动的时间为t==。
1
题号
2
3
4
5
6
7
8
9
10
11
[答案] (1)v0 (3)
11.(2024·江苏吴江中学高三期中)宽度为L=0.5 m 的光滑导轨固定在水平地面上,水平部分足够长,光滑倾斜部分与水平面的夹角为30°,两部分在PQ处平滑连接。导轨水平部分MN右侧区域有竖直方向的匀强磁场;倾斜部分有与导轨所在斜面垂直的匀强磁场(图中均未画出),两处磁场的磁感应强度大小都为B=2 T。导体棒ab和cd的质量都为m=0.2 kg,电阻阻值都为r=2 Ω。cd棒固定在距PQ位置x0=4 m处,将ab自高度h=1 m处由静止释放,到达PQ之前已达到匀速运动状态。已知重力加速度g取10 m/s2,导体棒经过PQ处的能量损失忽略不计,导轨电阻不计,求:
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
(1)ab棒到达PQ时速度大小;
(2)ab棒沿倾斜部分运动过程中ab棒产生的热量Q;
(3)ab棒停下时与cd棒的距离。
[解析] (1)cd棒固定,ab棒到达PQ之前已达到匀速运动状态,则mg sin 30°=BIL
I=
代入数据解得ab棒到达PQ时的速度大小v=4 m/s。
(2)根据能量守恒得,ab棒沿倾斜部分运动过程中回路产生的热量
Qz=mgh-mv2=0.4 J
ab棒产生的热量Q=Qz=0.2 J。
1
题号
2
3
4
5
6
7
8
9
10
11
(3)ab棒到达水平轨道后,设其未与cd棒相碰就停下,由动量定理得-BL·Δt=0-mv
其中====
解得ab棒在水平面上移动的距离为
x==3.2 m<4 m
则ab棒停下时与cd棒的距离为
s=x0-x=0.8 m。
1
题号
2
3
4
5
6
7
8
9
10
11
[答案] (1)4 m/s (2)0.2 J (3)0.8 m
谢 谢 !
第十章 电磁感应
第4节 电磁感应中动量、能量和图像问题
细研考点·突破题型
1.电磁感应中的能量转化
考点1 电磁感应中的能量问题
2.求解焦耳热Q的三种方法
3.求解电磁感应现象中能量问题的一般步骤
(1)在电磁感应中,切割磁感线的导体或磁通量发生变化的回路将产生感应电动势,该导体或回路就相当于电源。
(2)分析清楚有哪些力做功,就可以知道有哪些形式的能量发生了相互转化。
(3)根据能量守恒列方程求解。
[典例1] (应用功能关系解决电磁感应中的能量问题)(2024·江苏南京模拟考试)如图所示,平行光滑的金属导轨由斜面和水平两部分组成,两部分导轨由两小段光滑、绝缘的圆弧轨道(长度可忽略)平滑相连。斜面部分(与水平面夹角小于30°)由间距为L的导轨CE、DF构成,水平部分由两段足够长但不等宽的平行金属导轨连接构成。EG、FH段间距为L,内有与竖直方向成60°角斜向左上方的磁感应强度大小为2B的匀强磁场。MP、NQ段间距为2L,内有与竖直方向成60°角斜向右上方的磁感应强度大小为B的匀强磁场。导体棒
甲、乙的质量均为m、电阻均为R,导体棒乙静止于MP、NQ段,现使导体棒甲自斜面导轨上距水平导轨h高度处由静止释放,两导体棒在运动过程中始终垂直导轨,且与导轨保持良好接触。若稳定时导体棒甲未进入MP、NQ段,导轨电阻和空气阻力均可忽略不计。已知B=0.2 T,m=0.4 kg,h=0.45 m,L=0.2 m,R=0.2 Ω, g=10 m/s2,求:
(1)甲棒刚进入磁场时,乙棒的加速度;
(2)从甲棒进入磁场到两棒达到稳定的过程,通过乙棒的电荷量;
(3)从甲棒进入磁场到两棒达到稳定的过程,乙棒上产生的焦耳热。
[解析] (1)甲棒在斜面导轨下滑的过程,由机械能守恒定律得mgh=
甲棒刚进入磁场时切割磁感线产生的感应电动势为
E1=2B cos 60°·Lv0
由闭合电路欧姆定律可知,回路中产生的感应电流为I1=
对乙棒,由牛顿第二定律可得
B cos 60°·I1·2L=ma
联立可得,乙棒的加速度大小为
a=0.03 m/s2,方向水平向右。
(2)两棒稳定时,电路中电流为0,则
2B cos 60°·Lv1=B cos 60°·2Lv2
解得v1=v2
两棒受到的安培力满足Fa=Fb
且安培力方向相反,则两棒组成的系统动量守恒,可得mv0=mv1+mv2
对乙棒,根据动量定理有B cos 60°··2Lt=mv2
其中q=t
联立可得,通过乙棒的电荷量为q=15 C。
(3)从甲棒进入磁场到两棒达到稳定的过程中,根据能量守恒定律有=+Q总
解得Q总=0.9 J
则乙棒上产生的焦耳热为Q乙=Q总=0.45 J。
[答案] (1)0.03 m/s2,方向水平向右 (2)15 C (3)0.45 J
【典例1 教用·备选题】 (应用功能关系解决电磁感应中的能量问题)小明设计的电磁健身器的简化装置如图所示,两根平行金属导轨相距l=0.50 m,倾角θ=53°,导轨上端接一个R=0.05 Ω 的电阻。在导轨间长d=0.56 m 的区域内,存在方向垂直导轨平面向下的匀强磁场,磁感应强度B=2.0 T。质量m=4.0 kg的金属棒CD水平置于导轨上,用绝缘绳索通过定滑轮与拉杆GH相连。CD棒的初始位置与磁场区域的下边界相距x=0.24 m。 一位健身者用恒力F=80 N 拉动GH杆,CD棒由静止开始运动,上升过程中CD棒始终保持与导轨垂直。当CD棒到达磁场上边界时健身者松手,触发恢复装置使CD棒回到初始位置(重力加速度g取10 m/s2,sin 53°=0.8,不计其他电阻、摩擦力以及拉杆和绳索的质量)。求:
(1)CD棒进入磁场时速度v的大小;
(2)CD棒进入磁场时所受的安培力FA的大小;
(3)在拉升CD棒的过程中,健身者所做的功W和电阻产生的焦耳热Q。
[解析] (1)棒进入磁场前由牛顿第二定律有a==12 m/s2
进入磁场时的速度v==2.4 m/s。
(2)感应电动势E=Blv
感应电流I=
安培力FA=BIl
代入得FA==48 N。
(3)健身者做功W=F(x+d)=64 J
由牛顿第二定律得F-mg sin θ-FA=0
知CD棒在磁场区域做匀速运动
在磁场中运动时间为t=
焦耳热Q=I2Rt=26.88 J。
[答案] (1)2.4 m/s (2)48 N (3)64 J 26.88 J
[典例2] (应用能量守恒定律解决电磁感应中的能量问题)(2024·江苏淮阴中学模拟)如图所示,凸字形硬质金属线框质量为m,相邻各边互相垂直,且处于同一竖直平面内,ab边长为l,cd边长为2l,ab与cd平行,间距为2l。匀强磁场区域的上下边界均水平,磁场方向垂直于线框所在平面。开始时,cd边到磁场上边界的距离为2l,线框由静止释放,从cd边进入磁场直到ef、pq边进入磁场前,线框做匀速运动,在ef、pq边离开磁场后,ab边离开磁场之前,线框又做匀速运动。线框完全穿过磁场过程中产生的热量为Q。线框在下落过程中始终处于原竖直平面内,且ab、cd边保持水平,重力加速度为g。求:
(1)线框ab边将离开磁场时做匀速运动的速度大小是cd边刚进入磁场时的几倍;
(2)磁场上下边界间的距离H。
[解析] (1)设磁场的磁感应强度大小为B,cd边刚进入磁场时,线框做匀速运动的速度为v1,cd边上的感应电动势为E1,由法拉第电磁感应定律可得E1=2Blv1
设线框总电阻为R,此时线框中电流为I1,由闭合电路欧姆定律可得I1=
设此时线框所受安培力为F1,有F1=2I1lB
由于线框做匀速运动,故受力平衡,所以有mg=F1
联立解得v1=
设ab边离开磁场之前,线框做匀速运动的速度为v2,
同理可得v2=,故可知v2=4v1
即线框ab边将离开磁场时做匀速运动的速度大小是cd边刚进入磁场时的4倍。
(2)线框自释放直到cd边进入磁场前,由机械能守恒定律可得
2mgl=
线框完全穿过磁场的过程中,由能量守恒定律可得
mg(2l+H)=+Q
联立解得H=+28l。
[答案] (1)4倍 (2)+28l
【典例2 教用·备选题】 (应用能量守恒定律解决电磁感应中的能量问题)如图所示,竖直放置的“ ”形光滑导轨宽为L,矩形匀强磁场Ⅰ、Ⅱ的高和间距均为d,磁感应强度为B。质量为m的水平金属杆由静止释放,进入磁场Ⅰ和Ⅱ时的速度相等。金属杆在导轨间的电阻为R,与导轨接触良好,其余电阻不计,重力加速度为g。金属杆( )
A.刚进入磁场Ⅰ时加速度方向竖直向下
B.穿过磁场Ⅰ的时间小于在两磁场之间的运动时间
C.穿过两磁场产生的总热量为4mgd
D.释放时距磁场Ⅰ上边界的高度h可能小于
√
C [根据题述,由金属杆进入磁场Ⅰ和Ⅱ时的速度相等可知,金属杆在磁场Ⅰ中做减速运动,所以金属杆刚进入磁场Ⅰ时加速度方向竖直向上,A错误;由于金属杆进入磁场Ⅰ后做加速度逐渐减小的减速运动,而在两磁场之间做匀加速运动,所以穿过磁场Ⅰ的时间大于在两磁场之间的运动时间,B错误;根据能量守恒定律,金属杆从刚进入磁场Ⅰ到刚进入磁场Ⅱ过程动能变化量为0,重力做功为2mgd,则金属杆穿过磁场Ⅰ产生的热量Q1=2mgd,而金属杆在两磁场区域的运动情况相同,产生的热量相等,所以金属杆穿过两
磁场产生的总热量Q2=2×2mgd=4mgd,C正确;金属杆刚进入磁场Ⅰ时的速度v=,进入磁场Ⅰ时产生的感应电动势E=BLv,感应电流I=,所受安培力F=BIL,由于金属杆刚进入磁场Ⅰ时加速度方向竖直向上,所以安培力大于重力,即F>mg,联立解得h>,D错误。]
[典例3] (应用焦耳定律求电能) (2020·江苏卷)如图所示,电阻为0.1 Ω的正方形单匝线圈abcd的边长为0.2 m,bc边与匀强磁场边缘重合。磁场的宽度等于线圈的边长,磁感应强度大小为0.5 T,在水平拉力作用下,线圈以8 m/s的速度向右穿过磁场区域。求线圈在上述过程中:
(1)感应电动势的大小E;
(2)所受拉力的大小F;
(3)感应电流产生的热量Q。
[解析] (1)线圈切割磁感线产生的感应电动势 E=Blv
代入数据得E=0.8 V。
(2)线圈中产生的感应电流I=
拉力的大小等于安培力的大小,则F=BIl
解得F=
代入数据得F=0.8 N。
(3)运动时间t=
根据焦耳定律有Q=I2Rt
联立可得Q=
代入数据解得Q=0.32 J。
[答案] (1)0.8 V (2)0.8 N (3)0.32 J
【典例3 教用·备选题】 (应用焦耳定律求电能)光滑绝缘的水平面上有垂直于水平面的匀强磁场,磁场被分成区域Ⅰ和Ⅱ,宽度均为h,其俯视图如图(a)所示,两磁场磁感应强度随时间t的变化如图(b)所示,0~τ时间内,两区域磁场恒定,方向相反,磁感应强度大小分别为2B0和B0,一电阻为R、边长为h的刚性正方形金属框abcd平放在水平面上,ab、cd边与磁场边界平行。t=0时,金属框ab边刚好跨过区域Ⅰ的左边界以速度v向右运动。在τ时刻,ab边运动到距区域Ⅰ的左边界处,金属框的速度近似为零,此时金属框被固定,如图(a)中的虚线框所示。随后在τ~2τ时间内,Ⅰ区磁感应强度线性减小到0,Ⅱ区磁场保持不变;2τ~3τ时间内,Ⅱ区磁感应强度也线性减小到0。求:
(1)t=0时金属框所受的安培力F;
(2)t=1.2τ时穿过金属框的磁通量Φ;
(3)2τ~3τ时间内,金属框中产生的热量Q。
[解析] (1)由题图可知t=0时金属框切割磁感线的感应电动势为E=2B0hv+B0hv=3B0hv
则感应电流大小为I==
所受的安培力为
F=2B0h+B0h=
方向水平向左。
(2)在τ时刻,ab边运动到距区域Ⅰ的左边界处,金属框的速度近似为零,此时金属框被固定,则t=1.2τ时穿过金属框的磁通量为
Φ=1.6B0h·h-B0h·h=。
(3)2τ~3τ时间内,Ⅱ区磁感应强度也线性减小到0,则有E′===
感应电流大小为I′==
则2τ~3τ时间内,金属框中产生的热量为
Q=I′2RΔt=。
[答案] ,方向水平向左 (2)
[典例4] (功率的计算)如图所示,两条相距d的平行金属导轨位于同一水平面内,其右端接一阻值为R的电阻。质量为m的金属杆静置在导轨上,其左侧的矩形匀强磁场区域MNPQ的磁感应强度大小为B、方向竖直向下。当该磁场区域以速度v0匀速地向右扫过金属杆后,金属杆的速度变为v。导轨和金属杆的电阻不计,导轨光滑且足够长,杆在运动过程中始终与导轨垂直且两端与导轨保持良好接触。求:
(1)MN刚扫过金属杆时,杆中感应电流的大小I;
(2)MN刚扫过金属杆时,杆的加速度大小a;
(3)PQ刚要离开金属杆时,感应电流的功率P。
[解析] (1)MN刚扫过金属杆时,金属杆的感应电动势E=Bdv0 ①
回路中的感应电流I= ②
由①②式解得I=。 ③
(2)金属杆所受的安培力F=BId ④
对金属杆由牛顿第二定律得F=ma ⑤
由③④⑤式得a=。 ⑥
(3)金属杆切割磁感线的相对速度
v′=v0-v ⑦
感应电动势E=Bdv′ ⑧
感应电流的电功率P= ⑨
由⑦⑧⑨式得P=。 ⑩
[答案] (1) (2) (3)
1.对于两导体棒在平直的光滑导轨上运动的情况,如果两棒所受的外力之和为零,则考虑应用动量守恒定律处理问题。
2.由BL·Δt=m·Δv、q=·Δt可知,当题目中涉及电荷量或平均电流时,可应用动量定理来解决问题。
考点2 动量观点在电磁感应问题中的应用
[典例5] (动量观点在电磁感应问题中的应用)如图所示,两平行光滑长直金属导轨水平放置,间距为L。abcd区域有匀强磁场,磁感应强度大小为B,方向竖直向上。初始时刻,磁场外的细金属杆M以初速度v0向右运动,磁场内的细金属杆N处于静止状态。两金属杆与导轨接触良好且运动过程中始终与导轨垂直。两杆的质量均为m,在导轨间的电阻均为R,感应电流产生的磁场及导轨的电阻忽略不计。
(1)求M刚进入磁场时受到的安培力F的大小和方向;
(2)若两杆在磁场内未相撞且N出磁场时的速度为,求:
①N在磁场内运动过程中通过回路的电荷量q;
②初始时刻N到ab的最小距离x。
[解析] (1)细金属杆M以初速度v0向右刚进入磁场时,产生的动生电动势为
E=BLv0
感应电流大小为I=
则所受的安培力大小为F=BIL=
由左手定则可知安培力的方向水平向左。
(2)①金属杆N在磁场内运动过程中,设回路中的平均电流为,由动量定理得
BL·Δt=m·-0
且q=·Δt
联立解得q=。
②设两杆在磁场中相对靠近的位移为Δx,有
=
=
整理可得q=
联立解得Δx=
由于两杆未相撞,所以初始时刻N到ab的最小距离为x=Δx=。
[答案] (1) 方向水平向左 (2)① ②
规律总结 两金属杆在平直的光滑导轨上运动,只受到安培力作用,这类问题可以从以下三个观点来分析:
(1)力学观点:通常情况下一个金属杆做加速度逐渐减小的加速运动,而另一个金属杆做加速度逐渐减小的减速运动,最终两金属杆以共同的速度匀速运动。
(2)能量观点:其中一个金属杆动能的减少量等于另一个金属杆动能的增加量与回路中产生的焦耳热之和。
(3)动量观点:如果光滑导轨间距恒定,则两个金属杆所受的安培力大小相等,通常情况下系统的动量守恒。
[典例6] (动量定理在电磁感应现象中的应用)(2024·浙江1月选考)如图1所示,扫描隧道显微镜减振装置由绝缘减振平台和磁阻尼减振器组成。平台通过三根关于O′O″轴对称分布的相同轻杆悬挂在轻质弹簧的下端O,弹簧上端固定悬挂在O′点,三个相同的关于O′O″轴对称放置的减振器位于平台下方。如图2所示,每个减振器由通过绝缘轻杆固定在平台下表面的线圈和固定在桌面上能产生辐向磁场的铁磁体组成,辐向磁场分布关于线圈中心竖直轴对称,线圈所在处磁感应强度大小均为B。处于静止状态的平台受到外界微小扰动,线圈在磁场中做竖直方向的阻尼运动,其位移随时间变化的图
像如图3所示。已知t=0时速度为v0,方向向下,t1、t2时刻的振幅分别为A1、A2。平台和三个线圈的总质量为m,弹簧的劲度系数为k,每个线圈半径为r、电阻为R。当弹簧形变量为Δx时,其弹性势能为k(Δx)2。不计空气阻力,求:
(1)平台静止时弹簧的伸长量Δx;
(2)t=0时,每个线圈所受到安培力F的大小;
(3)在0~t1时间内,每个线圈产生的焦耳热Q;
(4)在t1~t2时间内,弹簧弹力冲量I弹的大小。
[解析] (1)平台静止时,三个线圈均不切割磁感线,线圈中不产生感应电流,线圈不受到安培力作用,O点受力平衡,因此由胡克定律可知此时弹簧的伸长量Δx=。
(2)在t=0时速度为v0,设每个线圈的周长为L,由法拉第电磁感应定律结合欧姆定律可得线圈中产生的感应电流
I====
每个线圈所受到安培力F的大小
F=BIL=。
(3)在0~t1时间内,由能量守恒定律得
Q′+mgA1=+k(Δx)2-k(Δx-A1)2
在0~t1时间内,振动时能量的减少转化为线圈的焦耳热,可知每个线圈产生的焦耳热
Q=Q′=。
(4)取向上为正方向,全程由动量定理可得
I弹+IA-mg(t2-t1)=0
IA=3×2πrB·Δq
Δq=
联立解得弹簧弹力冲量I弹的大小为
I弹=mg(t2-t1)-。
[答案] (1) (2) (4)mg(t2-t1)-
【典例6 教用·备选题】 (动量定理在电磁感应现象中的应用)(2025·无锡调研)两足够长且不计电阻的光滑金属轨道如图甲所示放置,间距为d=1 m,在左端弧形轨道部分高h=1.25 m 处放置一金属杆a,弧形轨道与平直轨道的连接处光滑无摩擦,在平直轨道右端放置另一金属杆b,杆a、b的电阻分别为 Ra=2 Ω、Rb=
5 Ω,在平直轨道区域有竖直向上的匀强磁场,磁感应强度B=
2 T。 现杆b以初速度大小v0=5 m/s 开始向左滑动,同时由静止释放杆a,杆a由静止滑到水平轨道的过程中,通过杆b的平均电流为0.3 A;从a下滑到水平轨道时开始计时,a、b运动的速度—时间图像如图乙所示(以a运动方向为正方向),其中ma=2 kg,mb=1 kg,g取10 m/s2,求:
(1)杆a在弧形轨道上运动的时间;
(2)杆a在水平轨道上运动过程中通过其截面的电荷量;
(3)在整个运动过程中杆b产生的焦耳热。
[解析] (1)设杆a由静止滑至弧形轨道与平直轨道连接处时杆b的速度大小为vb0,对杆b运用动量定理,有Bd·Δt=-mb(vb0-v0)
其中vb0=2 m/s
代入数据解得Δt=5 s。
(2)对杆a由静止下滑到平直导轨上的过程中,由机械能守恒定律有magh=
解得va==5 m/s
设最后a、b两杆共同的速度为v′,由动量守恒定律得mava-mbvb0=(ma+mb)v′
代入数据解得v′= m/s
杆a动量的变化量等于它所受安培力的冲量,设杆a的速度从va到v′的运动时间为Δt′,则由动量定理可得-BdI·Δt′=ma(v′-va)
而q=I·Δt′
代入数据得q= C。
(3)由能量守恒定律可知杆a、b中产生的焦耳热为
Q=-(mb+ma)v′2= J
杆b中产生的焦耳热为Q′=Q= J。
[答案] (1)5 s (2) C (3) J
【典例6 教用·备选题】 (动量定理在电磁感应现象中的应用)如图所示,与水平面夹角为θ的绝缘斜面上固定有光滑U形金属导轨。质量为m、电阻不可忽略的导体杆MN沿导轨向下运动,以大小为v的速度进入方向垂直于导轨平面向下的匀强磁场区域,在磁场中运动一段时间t后,速度大小变为2v。运动过程中杆与导轨垂直并接触良好,导轨的电阻忽略不计,重力加速度为g。杆在磁场中运动的此段时间内( )
A.流过杆的感应电流方向为从N到M
B.杆沿导轨下滑的距离为vt
C.流过杆的感应电流的平均电功率等于重力的平均功率
D.杆所受安培力的冲量大小为mgt sin θ-mv
√
D [根据右手定则,判断知流过杆的感应电流方向为从M到N,故A错误;依题意,设杆切割磁感线的有效长度为L,电阻为R,杆在磁场中运动的此段时间内,杆受到重力、导轨支持力及沿导轨向上的安培力作用,根据牛顿第二定律可得mg sin θ-F安=ma,F安=BIL,I=,联立可得杆的加速度a=g sin θ-,可知,杆在磁场中运动的此段时间内做加速度逐渐减小的加速运动,若杆做匀加速直线运动,则杆运动的距离为s=·t=vt,根据 v-t 图像
围成的面积表示位移,可知杆在时间t内速度由v达到2v,杆真实运动的距离大于匀加速情况运动的距离,即大于vt,故B错误;由于在磁场中运动的此段时间内,杆做加速度逐渐减小的加速运动,杆的动能增大,由动能定理可知,重力对杆所做的功大于杆克服安培力所做的功,根据=可得安培力的平均功率小于重力的平均功率,即流过杆感应电流的平均电功率小于重力的平均功率,故C错误;杆在磁场中运动的此段时间内,根据动量定理,可得mgt sin θ-I安=m·2v-mv,得杆所受安培力的冲量大小为I安=mgt sin θ-mv,故D正确。故选D。]
[典例7] (动量守恒定律在电磁感应中的应用)如图所示,在水平面内固定有两根相互平行的无限长光滑金属导轨,其间距为L,电阻不计。在虚线l1的左侧存在竖直向上的匀强磁场,在虚线l2的右侧存在竖直向下的匀强磁场,两部分磁场的磁感应强度大小均为B。ad、bc两根电阻均为R的金属棒与导轨垂直,分别位于两磁场中,现突然给ad棒一个水平向左的初速度v0,在两棒达到稳定的过程中,下列说法正确的是( )
A.两金属棒组成的系统的动量守恒
B.两金属棒组成的系统的动量不守恒
C.ad棒克服安培力做功的功率等于ad棒的发热功率
D.ad棒克服安培力做功的功率等于安培力对bc棒做功的功率与bc棒发热功率之和
√
B [开始时,ad棒以初速度v0切割磁感线,产生感应电动势,在回路中产生顺时针方向(俯视)的感应电流,ad棒因受到向右的安培力而减速,bc棒受到向右的安培力而向右加速;当两棒的速度大小相等,即两棒因切割磁感线而产生的感应电动势相等时,回路中没有感应电流,两棒各自做匀速直线运动;由于两棒所受的安培力都向右,两金属棒组成的系统所受合外力不为零,所以该系统的动量不守恒,A错误,B正确;根据能量守恒定律可知,ad棒动能的减小量等于回路中产生的热量和bc棒动能的增加量,由动能定理可知,ad棒动能的减小量等于ad棒克服安培力做的功,bc棒动能的增加量等于安培力对bc棒做的功,所以ad棒克服安培力做功的功率等于安培力对bc棒做功的功率与两棒总发热功率之和,C、D错误。]
[典例8] (三大观点的综合应用)(2024·湖北卷)如图所示,两足够长平行金属直导轨MN、PQ的间距为L,固定在同一水平面内,直导轨在左端M、P点分别与两条竖直固定、半径为L的圆弧导轨相切。MP连线与直导轨垂直,其左侧无磁场,右侧存在磁感应强度大小为B、方向竖直向下的匀强磁场。长为L、质量为m、电阻为R的金属棒ab跨放在两圆弧导轨的最高点。质量为2m、电阻为6R的均匀金属丝制成一个半径为L的圆环,水平放置在两直导轨上,其圆心到两直导轨的距离相等。忽略导轨的电阻、所有摩擦以及金属环的可能形变,金属棒、金属环均与导轨始终接触良好,重力加速度大小为g。现将金属棒ab由静止释放,求:
(1)ab刚越过MP时产生的感应电动势大小;
(2)金属环刚开始运动时的加速度大小;
(3)为使ab在整个运动过程中不与金属环接触,金属环圆心初始位置到MP的最小距离。
[解析] (1)设ab棒刚越过MP时速度大小为v1,产生的电动势大小为E1,对ab在圆弧导轨上运动的过程,由机械能守恒定律有
mgL=
ab刚越过MP时,由法拉第电磁感应定律得
E1=BLv1
联立解得E1=BL。
(2)经分析知金属环在导轨外的两段电阻被短路,由几何关系可知导轨之间两段金属环的电阻均为R,它们在电路中并联后的总电阻Rc=
设电路中初始的干路电流为I1,由闭合电路欧姆定律有I1=
经分析知整个金属环在运动过程中可视为长度为L、电阻为Rc的金属棒,设金属环刚开始运动时所受的安培力大小为F1、加速度大小为a,则
F1=I1LB
由牛顿第二定律得F1=2ma
联立解得a=。
(3)经分析,ab进入磁场后,ab和金属环组成的系统动量守恒,设两者共速时的速度大小为v2,由动量守恒定律得mv1=(m+2m)v2
设在极短时间Δt内,ab与金属环圆心的距离减少量为Δx,金属环所受安培力大小为F,流过ab的电流为I,整个电路的电动势为E,对金属环,由动量定理得=2mv2-0
又F=ILB
由闭合电路欧姆定律得I=
设金属环圆心初始位置到MP的最小距离为s,若ab与金属环共速时,两者恰好接触,金属环圆心初始位置到MP的距离最小,对ab进入磁场到两者共速的过程,由法拉第电磁感应定律有
E=BL
又s=L+
联立解得s=+L。
[答案] (1)BL (2)
(3)+L
【典例8 教用·备选题】(三大观点的综合应用)如图,两根足够长的光滑金属直导轨平行放置,导轨间距为L,两导轨及其所构成的平面均与水平面成θ角,整个装置处于垂直于导轨平面斜向上的匀强磁场中,磁感应强度大小为B。现将质量均为m的金属棒a、b垂直导轨放置,每根金属棒接入导轨之间的电阻均为R。运动过程中金属棒与导轨始终垂直且接触良好,金属棒始终未滑出导轨,导轨电阻忽略不计,重力加速度为g。
(1)先保持棒b静止,将棒a由静止释放,
求棒a匀速运动时的速度大小v0;
(2)在(1)问中,当棒a匀速运动时,再将棒b由静止释放,求释放瞬间棒b的加速度大小a;
(3)在(2)问中,从棒b释放瞬间开始计时,经过时间t0,两棒恰好达到相同的速度v,求速度v的大小,以及时间t0内棒a相对于棒b运动的距离Δx。
[解析] (1)金属棒a在运动过程中重力沿斜面的分力和棒a受到的安培力相等时做匀速运动,由法拉第电磁感应定律可得E=BLv0
由闭合电路欧姆定律及安培力公式可得
I=,F=BIL
由棒a受力平衡可得mg sin θ=BIL
联立解得v0=。
(2)由右手定则可知金属棒b中电流向里,由左手定则可知棒b受到沿斜面向下的安培力,此时电路中电流不变,则对棒b由牛顿第二定律可得mg sin θ+BIL=ma
解得a=2g sin θ。
(3)释放棒b后棒a受到沿斜面向上的安培力,在到达共速的过程对棒a由动量定理得
mg sin θt0-BLt0=mv-mv0
棒b受到向下的安培力,对棒b由动量定理得
mg sin θt0+BLt0=mv
联立解得v=g sin θt0+
此过程流过棒b的电荷量为q,则有q=t0
由法拉第电磁感应定律可得
==
联立可得Δx==。
[答案] (1) (2)2g sin θ
(3)g sin θt0+
电磁感应中常见的图像问题
考点3 电磁感应中的图像问题
图像类型 (1)随时间变化的图像,如B-t图像、Φ-t图像、E-t图像、I-t图像;
(2)随位移变化的图像,如E-x图像、I-x图像
(先看坐标轴:弄清哪个物理量随哪个物理量变化)
问题类型 (1)由给定的电磁感应过程选出或画出正确的图像(画图像);
(2)由给定的有关图像分析电磁感应过程,求解相应的物理量(用图像)
应用 知识 四个规律 左手定则、安培定则、右手定则、楞次定律
六类公式 (1)平均电动势E=n
(2)平动切割电动势E=Blv
(3)转动切割电动势E=Bl2ω
(4)闭合电路欧姆定律I=
(5)安培力F=BIl
(6)牛顿运动定律的相关公式等
[典例9] (根据电磁感应过程选择图像)空间中存在如图所示的磁场,Ⅰ、Ⅱ区域的宽度均为2R,磁感应强度大小均为B(Ⅰ区域磁场方向垂直纸面向里,Ⅱ区域磁场方向垂直纸面向外),半径为R的圆形导线框在外力作用下以速度v匀速通过磁场区域,设任意时刻导线框中电流为I(逆时针为正),导线框所受安培力为F(向左为正),从导线框刚进入Ⅰ区域开始将向右运动的位移记为x,则下列图像正确的是( )
A B
C D
√
D [当导线框在磁场Ⅰ区域向右运动过程中,设导线框切割磁感线的等效长度为l,则有(R-x)2+=R2,整理得l=2, 则导线框产生的感应电动势为E=Blv,感应电流为I==,可知电流与位移不成线性关系,B错误;当导线框圆心运动到Ⅰ、Ⅱ区域的边界时,此时产生的感应电流大小为I′==,即导线框在x=3R时的电流大
小为x=R时的两倍,方向沿着顺时针方向,A错误;通过分析可知,除了x=2R、x=4R、x=6R三个特殊位置,电流为0,受力为0,在0
A B
C D
√
B [金属棒cd在恒力F作用下由静止开始加速,此时金属棒ab、cd的加速度aa=0、ac=,之后回路中出现感应电流,金属棒cd受到的安培力与恒力F反向,金属棒cd的加速度减小,金属棒ab在安培力的作用下开始加速,金属棒cd与金属棒ab的速度差逐渐增大,回路中的电动势逐渐增大,安培力F安=,逐渐增大,金属棒ab加速度增大,当aa=ac时,vc-va不再变化,回路中的电流不再变化,但是两金属棒的速度仍在增大,故A正确,与题意不符,B
错误,与题意相符;设两金属棒电阻均为R,系统达到稳定之前,Ucd=BLva+IR,Ucd随时间逐渐增大,系统达到稳定后,因回路中电流不变,则Ucd=BLvc-IR,Ucd随着vc的增加而均匀增加,故C正确,与题意不符;闭合回路消耗的电功率P=2I2R,在开始阶段随回路中电流的增大,电功率逐渐增大,当系统稳定后回路中电流不变,电功率不再变化,故D正确,与题意不符。本题选错误的,故选B。]
方法技巧 电磁感应中图像选择类的两个常用方法
排除法 定性地分析电磁感应过程中物理量的变化趋势(增大还是减小)、变化快慢(均匀变化还是非均匀变化),特别是分析物理量的正负,以排除错误的选项。
函数法 根据题目所给条件定量地写出两个物理量之间的函数关系,然后由函数关系对图像进行分析和判断。
[典例10] (根据图像分析判断电磁感应过程)(2024·江苏南京一模)世界首个电磁驱动地面超高速试验设施——“电磁橇”在我国济南阶段性建成并成功运行,电磁橇可以将吨级及以上物体最高加速到 1 030 公里的时速,创造了大质量超高速电磁推进技术的世界最高速度纪录。电磁橇运用了电磁弹射的原理,图甲是一种电磁弹射装置的原理图,开关S先拨向1,直流电源向电容器充电,待电容器充好电后在t=0时刻将开关S拨向2,发射线圈被弹射出去,如图乙所示,电路中电流在t=t0时刻达到峰值后减小。假设发射线圈由粗细均匀的同种金属导线绕制而成,发射导管材质绝缘,管内光滑,下列说法正确的是( )
A.在0~t0时间内,发射线圈的加速度不断增大
B.在0~t0时间内,发射线圈中的电流不断增大
C.增加发射线圈的匝数,发射线圈加速度不变
D.发射导管越长,发射线圈的出射速度越大
√
C [在0~t0时间内,驱动线圈中的电流逐渐变大,但是电流的变化率逐渐减小,则穿过发射线圈的磁通量的变化率逐渐减小,则发射线圈中产生的电流不断减小,在t=t0时刻发射线圈中的电流减小为0,根据F=BIL可知,发射线圈所受的安培力不是不断增大,则发射线圈的加速度不是不断增大,故A、B错误;根据E=n,设单匝线圈的电阻为r0,质量为m0,线圈的半径为r,则电流为I==,安培力为F=nBI·2πr,加速度为a===,则增加发射线圈的匝数,发射线圈加速度不变,故C正确;对发射线圈根据动量定理可得F安t=mv,而F安t=nBLt=nBL, 则安培力的冲量以及发射线圈的出射速度与发射导管的长度无关,故D错误。故选C。]
【典例10 教用·备选题】 (根据图像分析判断电磁感应过程)(2024·锡山模拟)如图甲所示,在水平面上固定一个匝数为10匝的等边三角形金属线框,总电阻为 3 Ω, 边长为0.4 m。金属框处于两个半径为0.1 m的圆形匀强磁场中,顶点A恰好位于左边圆的圆心,BC边的中点恰好与右边圆的圆心重合。左边磁场方向垂直纸面向外,右边磁场方向垂直纸面向里,磁感应强度的变化规律如图乙所示,磁场方向垂直纸面向里为正方向,则下列说法中正确的是(π取3)( )
A.线框中感应电流的方向是顺时针方向
B.t=0.4 s时,穿过线框的磁通量为0.005 Wb
C.经过t=0.4 s,线框中产生的热量为0.3 J
D.前0.4 s内流过线框某截面的电荷量为 0.4 C
√
C [根据楞次定律和安培定则,线框中感应电流的方向是逆时针方向,A错误;0.4 s时穿过线框的磁通量Φ=Φ1-Φ2=πr2·B1-πr2·B2=0.055 Wb,B错误;由题图乙知==10 T/s, 根据法拉第电磁感应定律,感应电动势E=n=n·πr2·=
1.5 V,感应电流I==0.5 A,0.4 s内线框中产生的热量Q=I2Rt=0.3 J,C正确;前 0.4 s 内流过线框某截面的电荷量q=It=0.2 C,D错误。]
【典例10 教用·备选题】 (根据图像分析判断电磁感应过程)如图(a)所示,在同一平面内固定有一长直导线PQ和一导线框R,R在PQ的右侧。导线PQ中通有正弦交流电i,i的变化如图(b)所示,规定从Q到P为电流正方向。导线框R中的感应电动势( )
A.在t=时最大
B.在t=时改变方向
C.在t=时最大,且沿顺时针方向
D.在t=T时最大,且沿顺时针方向
√
C [因通电导线的磁感应强度大小正比于电流的大小,故导线框R中磁感应强度与时间的变化关系类似于题图(b),感应电动势正比于磁感应强度的变化率,即题图(b)中的切线斜率,斜率的正负反映感应电动势的方向,斜率的绝对值反映感应电动势的大小。由题图(b)可知,电流为零时,感应电动势最大,电流最大时,感应电动势改变方向,A、B错误;再由楞次定律可判断在一个周期内,~时间内感应电动势的方向沿顺时针,时刻最大,C正确;其余时间段感应电动势沿逆时针方向,D错误。]
[典例11] (电磁感应中图像的转换)(2024·江苏无锡一模)如图1所示,绝缘细线的下端悬挂着一金属材料做成的空心心形挂件,该挂件所在空间水平直线MN下方存在匀强磁场,初始时刻磁场方向垂直挂件平面向里,且大小随时间的变化如图2所示。若某段时间内挂件处于静止状态,则该段时间内挂件中产生的感应电流的大小i、通过线框某一横截面的电荷量Q、挂件所受安培力F的大小、细线拉力T的大小随时间t变化的规律不可能是( )
A B
C D
√
D [根据法拉第电磁感应定律可得感应电动势为E==S有=kS有,可知感应电动势保持不变,设空心心形挂件的电阻为R,则电流为I=,可知挂件中产生的感应电流保持不变;根据Q=It可知Q-t图像为过原点的倾斜直线;根据F=BIL有知,由于B随时间均匀减小,则安培力F随时间均匀减小,故A、B、C正确,不满足题意要求。穿过空心心形挂件的磁通量向里减小,根据楞次定律可知,挂件中感应电流方向为顺时针方向,根据左手定则可知,安培力方向竖直向下,根据受力平衡可得T=mg+F,由于安培力F随时间均匀减小,则细线拉力T随时间均匀减小,但拉力T不会减小到0,故D错误,满足题意要求。故选D。]
【典例11 教用·备选题】 (电磁感应中图像的转换)有一磁场方向竖直向下,磁感应强度B随时间t的变化关系如图甲所示。现有如图乙所示的直角三角形导线框abc水平放置,放在匀强磁场中保持静止不动,t=0时刻,磁感应强度B的方向垂直纸面向里,设产生的感应电流i顺时针方向为正方向,竖直边ab所受安培力F的方向水平向左为正方向。则下面关于F和i随时间t变化的图像正确的是
( )
A B
C D
√
A [在0~3 s时间内,磁感应强度随时间线性变化,由法拉第电磁感应定律可知,感应电动势恒定,回路中感应电流恒定, 同时由F=BIL知道,电流恒定,安培力与磁感应强度成正比, 又由楞次定律判断出回路中感应电流的方向应为顺时针方向,即正方向, 故D错误;在3~4 s时间内,磁感应强度恒定,感应电动势等于零,感应电流为零,安培力等于零,故B、C错误;4~7 s时间内,磁感应强度随时间线性变化,由法拉第电磁感应定律可知,感应电动势恒定,回路中感应电流恒定,安培力与磁感应强度成正比,故A正确。]
规律总结 “四明确、一理解”巧解图像问题
题组一 电磁感应中的能量问题
1.如图所示,两条电阻不计的平行光滑导轨竖直放置在垂直纸面向里的匀强磁场内,已知磁感应强度B=0.5 T,导体棒ab、cd的长度均为 0.2 m, 电阻均为0.1 Ω,重力均为 0.1 N。 现用力向上拉动导体棒ab,使之匀速上升(导体棒ab、cd与导轨接触良好),此时cd静止不动。则在ab上升时,下列说法正确的是( )
1
题号
2
3
4
5
6
7
8
9
10
11
课时分层作业(三十一) 电磁感应中动量能量问题和图像问题
A.ab受到的拉力大小为2 N
B.ab向上运动的速度为2 m/s
C.在2 s内,拉力做功,有0.5 J的机械能转化为电能
D.在2 s内,拉力做功为0.6 J
1
题号
2
3
4
5
6
7
8
9
10
11
√
B [对导体棒cd分析:mg=BIl=,代入数据解得 v=2 m/s,B正确;对导体棒ab分析:F=mg+BIl=0.2 N,A错误;在2 s内拉力做功转化为ab棒的重力势能和电路中的电能,电能等于克服安培力做的功,即W电=F安vt==0.4 J,C错误;在2 s内拉力做的功为W拉=Fvt=0.8 J,D错误。]
1
题号
2
3
4
5
6
7
8
9
10
11
2.如图所示,竖直平面内在A、D两点各固定一颗光滑钉子,一个由细软导线制成的闭合导线框挂在两颗钉子上,匀强磁场的磁感应强度为B,导线框的电阻为r,圆的半径为R。重物通过绝缘动滑轮挂在导线框上。从t=0时刻开始,将导线上的C点绕圆心O以恒定角速度ω从A点沿圆弧移动到D点,导线始终绷紧。
此过程导线中( )
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
A.张力保持不变
B.感应电流的方向先顺时针后逆时针
C.感应电流i随时间t的变化关系为i=
D.产生的电热为
√
D [对滑轮分析可知,两边绳子拉力总是相等的,则两边绳子与竖直方向的夹角总相等,随着C点沿圆弧从A点移到D点,AC段与CD段绳子长度之和先增加后减小,则AE段与ED段绳子长度之和先减小后增加,AE段绳子与ED段绳子的夹角先增加后减小,由2T cos α=mg可知,绳子的张力先增加后减小,故A错误;设C点转过的角度为θ=ωt,根据几何知识可得,线框上的三角形的面积为S=
1
题号
2
3
4
5
6
7
8
9
10
11
·2R·R sin θ=R2sin θ,磁通量为Φ=BS=BR2sin θ,因θ角从0°到180°,则导线框中的磁通量先增大后减小,根据楞次定律可知,感应电流先沿逆时针方向,后沿顺时针方向,故B错误;根据法拉第电磁感应定律E=可知,导线框中感应电动势随时间t的变化关系为e=ωBR2cos ωt,感应电流随时间t的变化关系为i=,故C错误;导线框中感应电动势的有效值为E=,故导线框中产生的电热为Q==,故D正确。故选D。]
1
题号
2
3
4
5
6
7
8
9
10
11
3.如图所示,水平面上固定着两根相距L且电阻不计的足够长的光滑金属导轨,导轨处于方向竖直向下、磁感应强度为B的匀强磁场中,铜棒a、b的长度均等于两导轨的间距、电阻均为R、质量均为m,铜棒平行地静止在导轨上且与导轨接触良好,现给铜棒a一个平行导轨向右的瞬时冲量I,关于此后的过程,下列说法正确的是
( )
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
A.回路中的最大电流为
B.铜棒b的最大加速度为
C.铜棒b获得的最大速度为
D.回路中产生的总焦耳热为
√
B [由题意知a获得冲量I时速度最大,即va=,此后a在安培力作用下做减速运动,b在安培力作用下做加速运动,回路中产生的电动势E=BL(va-vb),可知a刚获得冲量时回路中产生的感应电流最大,即Im==,故A错误;开始时b所受安培力最大,即Fm=BImL=,则b的最大加速度am= =,故B正确;由题意知,a做减速运动,b做加速运动,当a、b速度相等时,两棒同时向右做匀速直线运动,根据动量守恒定律可知,I=2mvab,即vab=,此速度亦为b的最大速度,故C错误;根据系统能量守恒,则有=+Q,即Q=,故D错误。]
1
题号
2
3
4
5
6
7
8
9
10
11
题组二 动量观点在电磁感应问题中的应用
4.如图所示,在光滑的水平面上宽度为L的区域内,有垂直水平面向里的匀强磁场。现有一个边长为a(a
C.小于 D.以上均有可能
1
题号
2
3
4
5
6
7
8
9
10
11
√
B [通过线圈横截面的电荷量为q=Δt=
t,则-Baq=mv-mv0,-Baq=-mv,解得v=。故选B。]
1
题号
2
3
4
5
6
7
8
9
10
11
5.如图甲所示,水平面上有两根足够长的光滑平行金属导轨MN和PQ,两导轨间距为l,电阻均可忽略不计。在M和P之间接有阻值为R的定值电阻,导体杆ab质量为m、电阻为r,并与导轨接触良好。整个装置处于方向竖直向上、磁感应强度大小为B的匀强磁场中。现给杆ab一个初速度v0,使杆向右运动。则( )
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
A.当杆ab刚具有初速度v0时,杆ab两端的电压U=,且b点电势高于a点电势
B.通过电阻R的电流I随时间t的变化率的绝对值逐渐增大
C.若将M和P之间的电阻R改为接一电容为C的电容器,如图乙所示,同样给杆ab一个初速度v0,使杆向右运动,则杆ab稳定后的速度为v=
D.在C选项中,杆稳定后b点电势高于a点电势
√
C [当杆ab刚具有初速度v0时,其切割磁感线产生的感应电动势E=Blv0,杆ab两端的电压U==,根据右手定则知,感应电流的方向为b到a,杆ab相当于电源,a相当于电源的正极,则a点电势高于b点电势,A错误;通过电阻R的电流I=,由于杆ab速度减小,则电流减小,安培力减小,所以杆ab做加速度逐渐减小的减速运动,速度v随时间t的变化率的绝对值逐渐减小,则通过电阻R的电流I随时间t的变化率的绝对值逐渐减小,B错误;当杆ab以初速度v0开始切割磁感线时,电路开始给电容器充电,有电流通过杆ab,
1
题号
2
3
4
5
6
7
8
9
10
11
杆在安培力的作用下做减速运动,随着速度减小,安培力减小,加速度也减小,当电容器两端电压与感应电动势相等时,充电结束,杆以恒定的速度做匀速直线运动,电容器两端的电压U=Blv,而q=CU,对杆ab,根据动量定理得-Bl·Δt=mv-mv0,联立可得v=,C正确;杆稳定后,电容器不再充电,回路中没有电流,根据右手定则知,a点的电势高于b点电势,D错误。]
1
题号
2
3
4
5
6
7
8
9
10
11
题组三 电磁感应中的图像问题
6.(2025·江苏徐州模拟)如图甲所示,有一足够长的水平、平行金属轨道,轨道间距为L=1 m,整个轨道位于竖直向上的匀强磁场中,轨道电阻可忽略不计。轨道左端连接一阻值R=0.2 Ω的定值电阻,有一阻值r=0.2 Ω(导轨间部分)、质量m=1×10-2 kg的导体棒放在轨道上,导体棒长度大于L,导体棒与轨道间的动摩擦因数μ=0.2。现有一大小为6×10-2 N、垂直导体棒的水平恒力F作用在导体棒上,使其从静止开始运动。导体棒运动过程中,0~t时间通过电阻的电荷量q与时间t的关系如图乙所示,其中0~0.3 s为曲线,0.3~0.4 s为直线,已知导体棒始终与轨道垂直,重力加速度取g=10 m/s2, 下列说法正确的是( )
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
A.导体棒的最大速度为0.2 m/s
B.磁感应强度大小为0.4 T
C.0~0.3 s时间内,电阻上产生的热量为2.4×10-3 J
D.0~0.3 s时间内,导体棒的位移大小为8×10-2 m
√
D [0.3~0.4 s时间内,电荷量随时间均匀增加,电流稳定,即导体棒开始做匀速直线运动,达到最大运动速度,此时I===0.2 A,F=μmg+BIL,联立解得B==0.2 T,vm=0.4 m/s, A、B错误;0~0.3 s时间内,导体棒在外力作用下做加速度减小的加速运动,对导体棒由动量定理得Ft1-μmgt1-t1=mvm-0,即Ft1-μmgt1-=mvm-0,解得x=8×10-2 m,由动能定理得=-0,而Q总=,QR=Q总,联立解得QR=1.2×10-3 J,C错误,D正确。故选D。]
1
题号
2
3
4
5
6
7
8
9
10
11
7.(2024·江苏南京一模)如图所示,两根足够长的平行光滑金属导轨电阻不计,水平固定在竖直向上的匀强磁场中,导轨上垂直静置两根质量与电阻都相同的导体棒ab、cd。给ab棒平行于导轨的初速度并开始计时,棒ab、cd中产生的感应电动势eab、ecd、回路中的感应电流i、导轨间的电压u与时间t的关系图像中,可能正确的是
( )
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
A B
C D
√
D [设磁感应强度为B,两导体棒的质量均为m、接入电路的长度均为d、电阻均为R,导体棒ab的初速度为v0,某时刻t,导体棒ab、cd的速度分别为v1、v2,回路中的感应电流为i,由法拉第电磁感应定律有eab=Bdv1,ebc=Bdv2,i=,两导体棒受到的安培力大小为F=Bdi,方向与棒ab运动方向相反,与棒cd运动方向相同,棒ab减速、棒cd加速,v1减小、v2增大,(v1-v2)减小,电流i减小,
1
题号
2
3
4
5
6
7
8
9
10
11
F=Bdi减小,棒运动的加速度减小,即棒ab做初速为v0、加速度逐渐减小的减速运动,由eab=Bdv1可知eab减小得越来越慢,最终趋于,故A错误;棒cd做初速为零、加速度逐渐减小的加速运动,由ecd=Bdv2可知ecd由零开始增加得越来越慢,最终趋于恒定,故B错误;依题意,(v1-v2)越来越小,最终趋近于零,故i趋近于零,故C错误;两导轨间的电压u=eab-iR,对两棒由动量守恒定律有mv0=mv1+mv2,联立解得u=,可知u恒定,故D正确。故选D。]
1
题号
2
3
4
5
6
7
8
9
10
11
8.如图甲所示,在倾斜角为θ的光滑斜面内分布着垂直于斜面的匀强磁场,以垂直于斜面向上为磁感应强度正方向,其磁感应强度B随时间变化的规律如图乙所示。质量为m的矩形金属框从t=0时刻由静止释放,t3时刻的速度为v,移动的距离为L,重力加速度为g。在金属框下滑的过程中,下列说法正确的是( )
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
A.t1~t3时间内金属框中的电流方向先顺时针再逆时针方向
B.0~t3时间内金属框做匀加速直线运动
C.0~t3时间内金属框做加速度逐渐减小的直线运动
D.0~t3时间内金属框中产生的焦耳热为mgL sin θ-mv2
√
B [t1~t3时间内穿过金属框的磁通量先垂直于斜面向上减小,后垂直于斜面向下增大,根据楞次定律可知,金属框中的电流方向不变,A错误;0~t3时间内,金属框的ab边与cd边所受安培力等大反向,金属框所受安培力为零,则所受的合力沿斜面向下,大小为mg sin θ,做匀加速直线运动,B正确,C错误;0~t3时间内,金属框所受的安培力为零,金属框的机械能守恒,有mgL sin θ=mv2,而金属框中产生的焦耳热不为零,故金属框中产生的焦耳热不等于mgL sin θ-mv2,D错误。]
1
题号
2
3
4
5
6
7
8
9
10
11
9.(2024·江西卷节选)如图所示,绝缘水平面上固定一光滑平行金属导轨,导轨左右两端分别与两粗糙的倾斜平行金属导轨平滑连接,两侧导轨倾角分别为θ1、θ2,导轨间距均为l=2 m,水平导轨所在区域存在竖直向上的匀强磁场,磁感应强度大小B=0.5 T。 现有两均匀金属细杆甲和乙,质量分别为m1=6 kg和m2=2 kg,接入导轨的电阻均为R=1 Ω。 左、右两侧倾斜导轨与两棒的动摩擦因数分别为μ1=、μ2=。初始时刻,乙静止在水平导轨上,与水平导轨左端P1P2的距离为d,甲从左侧倾斜导轨高度h=4 m的位置静止滑下。水平导轨足够长,两棒运动过程中始终与导轨接触良好且保持垂直。若两棒发生碰撞,则为完全非弹性碰撞。不计空气阻力和导轨的电阻。(g取10 m/s2,sin θ1=0.6,sin θ2=0.8)
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
(1)求甲刚进入磁场时乙的加速度大小和方向;
(2)为使乙第一次到达水平导轨右端Q1Q2之前甲和乙不相撞,求d的最小值。
[解析] (1)对甲从静止运动至水平导轨的过程,根据动能定理有
m1gh-μ1m1g cos θ1·=-0
甲刚进入磁场时,由法拉第电磁感应定律有
E0=Blv0
则根据欧姆定律可知此时回路中的感应电流为
I0=
根据楞次定律可知,回路中的感应电流沿逆时针方向(俯视),结合左手定则可知,乙所受安培力方向水平向右,由牛顿第二定律有BI0l=m2a乙0
代入数据有a乙0=2 m/s2,方向水平向右。
1
题号
2
3
4
5
6
7
8
9
10
11
(2)甲和乙在磁场中运动的过程中,系统不受外力作用,则系统动量守恒,若两者共速时恰不相碰,则有
m1v0=(m1+m2)v共
对乙根据动量定理有Blt=m2v共-0
其中t=q=
联立解得dmin=Δx=24 m。
1
题号
2
3
4
5
6
7
8
9
10
11
[答案] (1)2 m/s2,方向水平向右 (2)24 m
10.如图所示,水平桌面上固定一光滑U形金属导轨,其平行部分的间距为l,导轨的最右端与桌子右边缘对齐,导轨的电阻忽略不计。导轨所在区域有方向竖直向上的匀强磁场,磁感应强度大小为B。一质量为m、电阻为R、长度也为l的金属棒P静止在导轨上。导轨上质量为3m的绝缘棒Q位于P的左侧,以大小为v0的速度向P运动并与P发生弹性碰撞,碰撞时间很短。碰撞一次后,P和Q先后从导轨的最右端滑出导轨,并落在地面上同一地点。P在导轨上运动时,两端与导轨接触良好,P与Q始终平行。不计空气阻力。求:
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
(1)金属棒P滑出导轨时的速度大小;
(2)金属棒P在导轨上运动过程中产生的热量;
(3)与P碰撞后,绝缘棒Q在导轨上运动的时间。
[解析] (1)由于绝缘棒Q与金属棒P发生弹性碰撞,根据动量守恒和能量守恒定律可得
3mv0=3mvQ+mvP
=
联立解得vP=v0,vQ=v0
由题知,碰撞一次后,P和Q先后从导轨的最右端滑出导轨,并落在地面上同一地点,则金属棒P滑出导轨时的速度大小等于绝缘棒Q滑出导轨时的速度大小,即v′P=vQ=v0。
1
题号
2
3
4
5
6
7
8
9
10
11
(2)根据能量守恒定律有=+Q
解得Q=。
(3)P、Q碰撞后,对金属棒P分析,根据动量定理得-BlΔt=mv′P-mvP
又q====
联立可得x=
由于Q为绝缘棒,无电流通过,不受安培力作用,做匀速直线运动,故Q运动的时间为t==。
1
题号
2
3
4
5
6
7
8
9
10
11
[答案] (1)v0 (3)
11.(2024·江苏吴江中学高三期中)宽度为L=0.5 m 的光滑导轨固定在水平地面上,水平部分足够长,光滑倾斜部分与水平面的夹角为30°,两部分在PQ处平滑连接。导轨水平部分MN右侧区域有竖直方向的匀强磁场;倾斜部分有与导轨所在斜面垂直的匀强磁场(图中均未画出),两处磁场的磁感应强度大小都为B=2 T。导体棒ab和cd的质量都为m=0.2 kg,电阻阻值都为r=2 Ω。cd棒固定在距PQ位置x0=4 m处,将ab自高度h=1 m处由静止释放,到达PQ之前已达到匀速运动状态。已知重力加速度g取10 m/s2,导体棒经过PQ处的能量损失忽略不计,导轨电阻不计,求:
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
(1)ab棒到达PQ时速度大小;
(2)ab棒沿倾斜部分运动过程中ab棒产生的热量Q;
(3)ab棒停下时与cd棒的距离。
[解析] (1)cd棒固定,ab棒到达PQ之前已达到匀速运动状态,则mg sin 30°=BIL
I=
代入数据解得ab棒到达PQ时的速度大小v=4 m/s。
(2)根据能量守恒得,ab棒沿倾斜部分运动过程中回路产生的热量
Qz=mgh-mv2=0.4 J
ab棒产生的热量Q=Qz=0.2 J。
1
题号
2
3
4
5
6
7
8
9
10
11
(3)ab棒到达水平轨道后,设其未与cd棒相碰就停下,由动量定理得-BL·Δt=0-mv
其中====
解得ab棒在水平面上移动的距离为
x==3.2 m<4 m
则ab棒停下时与cd棒的距离为
s=x0-x=0.8 m。
1
题号
2
3
4
5
6
7
8
9
10
11
[答案] (1)4 m/s (2)0.2 J (3)0.8 m
谢 谢 !
同课章节目录
