【江苏专版】55 第十三章 第1节 光的折射 全反射 课件《高考快车道》2026高考物理一轮总复习
文档属性
| 名称 | 【江苏专版】55 第十三章 第1节 光的折射 全反射 课件《高考快车道》2026高考物理一轮总复习 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-12-04 16:10:23 | ||
图片预览








文档简介
(共109张PPT)
第十三章 光 电磁波
第十三章 光 电磁波
知能模块 考点内容 高考(江苏卷)六年命题情况对照分析
2019-2024 命题分析
第1节 光的折射 全反射 光的折射 2019T13(3):光的全反射、临界角 2020T13(2):全反射 2021适应考T2:光的折射 2021T7:光的折射 2022T12:光的折射 2023T5:光的折射 高考对本章的考查以计算题为主,有时也会考选择题和填空题。考查的重点是光的折射定律、光的全反射的综合应用。
全反射
第十三章 光 电磁波
知能模块 考点内容 高考(江苏卷)六年命题情况对照分析
2019-2024 命题分析
第2节 光的波动性 电磁波 光的干涉 2020T13(1)(3):电磁波的应用、电磁波波长与频率的关系 2021适应考T1:光的偏振 2021T6:光的干涉 2023T6:光的干涉 2024T2:光的偏振 2024T6:光的折射 高考对本章的考查以计算题为主,有时也会考选择题和填空题。考查的重点是光的折射定律、光的全反射的综合应用。
光的衍射
光的偏振、激光
电磁振荡
第十三章 光 电磁波
知能模块 考点内容 高考(江苏卷)六年命题情况对照分析
2019-2024 命题分析
第2节 光的波动性 电磁波 电磁场与电磁波 2020T13(1)(3):电磁波的应用、电磁波波长与频率的关系 2021适应考T1:光的偏振 2021T6:光的干涉 2023T6:光的干涉 2024T2:光的偏振 2024T6:光的折射 高考对本章的考查以计算题为主,有时也会考选择题和填空题。考查的重点是光的折射定律、光的全反射的综合应用。
无线电波的发射与接收
电磁波谱
实验十八 测量玻璃的折射率
实验十九 用双缝干涉实验测量光的波长
第1节
光的折射 全反射
链接教材·夯基固本
一、光的折射定律 折射率
1.折射现象
光从一种介质____入另一种介质时传播方向发生____的现象,如图所示(以光从空气射入水中为例)。
斜射
改变
2.折射定律
(1)内容:折射光线与入射光线、法线处在________内,折射光线与入射光线分别位于法线的____;入射角的正弦与折射角的正弦成__比。
(2)表达式:=n。
[温馨提示] ①在光的折射现象中,光路是可逆的。
②当光从真空(或空气)斜射入某种介质时,入射角大于折射角;当光由介质斜射入真空(或空气)时,入射角小于折射角。
同一平面
两侧
正
3.折射率
(1)折射率是反映介质的____性质的物理量。
(2)定义式:n=。
(3)计算式:n=,因为v4.折射率的理解
(1)折射率由________性质决定,与入射角的大小____。
(2)折射率与介质的____没有关系,光密介质不是指密度大的介质。
(3)同一种介质中,频率越大的色光折射率越__,传播速度越__。
光学
大于
介质本身
无关
密度
大
小
二、全反射
1.定义:光从光密介质射入____介质,当入射角增大到某一角度时,折射光线全部____,只剩下反射光线的现象。
2.条件
(1)光从光密介质射入____介质。
(2)入射角__________临界角。
光疏
消失
光疏
大于或等于
3.临界角
(1)定义:折射角等于____时的入射角。
(2)公式:sin C=。若光从光密介质(折射率为n)射向真空或空气时,发生全反射的临界角为C,由n=得sin C=。
(3)大小:介质的折射率n越大,发生全反射的临界角C越__。
90°
小
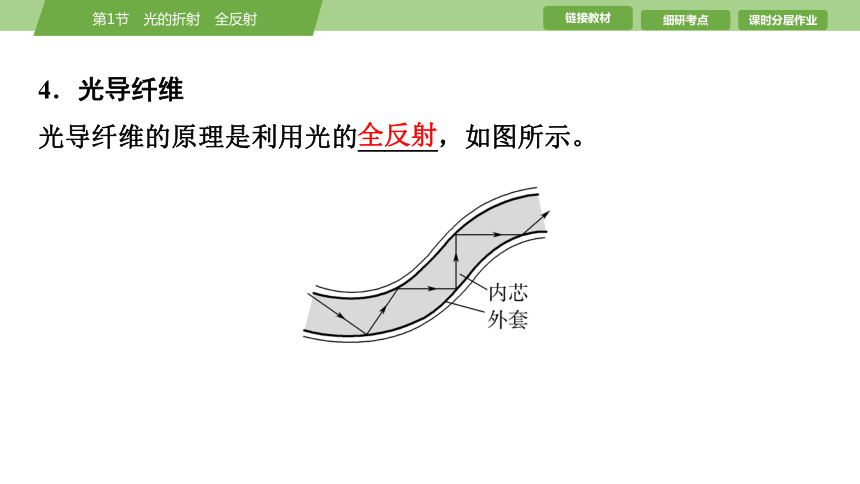
4.光导纤维
光导纤维的原理是利用光的______,如图所示。
全反射
三、光的色散
1.光的色散现象:含有多种颜色的光被分解为单色光的现象。
2.光谱:含有多种颜色的光被分解后,各种色光按其波长有序排列。
3.光的色散现象说明
(1)白光为复色光;
(2)同一介质对不同色光的折射率不同,频率越大的色光折射率____;
(3)不同色光在同一介质中的传播速度不同,波长越短,波速____。
越大
越慢
一、易错易误辨析(正确的打“√”,错误的打“×”)
(1)某种玻璃对蓝光的折射率比红光大,蓝光和红光以相同的入射角从空气斜射入该玻璃中,蓝光的折射角较大。 ( )
(2)在水中,蓝光的传播速度大于红光的传播速度。 ( )
(3)在潜水员看来,岸上的所有景物都出现在一个倒立的圆锥里。 ( )
×
×
√
(4)光从空气射入玻璃时,只要入射角足够大就可能发生全反射。 ( )
(5)光纤通信利用了全反射的原理。 ( )
(6)晚上,在池水中同一深度的两点光源分别发出红光和蓝光,水面上的人看蓝光光源浅一些。 ( )
×
√
√
二、教材习题衍生
1.(光的折射)有一正三角形OPQ玻璃砖,某束光线垂直于OP射入,恰好在PQ界面发生全反射,则玻璃砖的折射率( )
A. B. C. D.2
√
C [光路图如图所示,根据几何关系可知光线在PQ界面的入射角为C=60°,根据全反射的临界条件可得 sin C=,解得n=。故选C。]
2.(光的全反射的应用)如图所示是一个用折射率n=2.4的透明介质做成的四棱柱的横截面图,其中∠A=∠C=90°,∠B=60°,现有一束光从图示的位置垂直入射到棱镜的AB面上。(注意:每个面的反射光线和折射光线都不能忽略)则
以下说法正确的是( )
A.入射光有可能从DC边射出
B.入射光有可能从AB边射出
C.入射光不可能从BC边垂直射出
D.入射光从BC边垂直射出
√
细研考点·突破题型
1.对折射率的理解
(1)公式n=中,不论光是从真空射入介质,还是从介质射入真空,θ1总是真空中的光线与法线间的夹角,θ2总是介质中的光线与法线间的夹角。
(2)折射率的大小不仅反映了介质对光的折射本领,也反映了光在介质中传播速度的大小,v=。
考点1 折射定律和折射率的理解及应用
(3)折射率与入射角的大小无关,与介质的密度无关,光密介质不是指密度大的介质。
(4)折射率的大小不仅与介质本身有关,还与光的频率有关。同一种介质中,频率越大的色光折射率越大,传播速度越小。
(5)同一种色光,在不同介质中虽然波速、波长不同,但频率不变。
2.光路的可逆性:在光的折射现象中,光路是可逆的。如果让光线逆着原来的折射光线射到界面上,光线就会逆着原来的入射光线发生折射。
[典例1] (折射定律的应用)(2024·山东卷)某光学组件横截面如图所示,半圆形玻璃砖圆心为O点,半径为R;直角三棱镜FG边的延长线过O点,EG边平行于AB边且长度等于R,∠FEG=30°。横截面所在平面内,单色光线以θ角入射到EF边发生折射,折射光线垂直EG边射出。已知玻璃砖和三棱镜对
该单色光的折射率均为1.5。
(1)求sin θ;
(2)以θ角入射的单色光线,若第一次到达半圆弧AMB可以发生全反射,求光线在EF上入射点D(图中未标出)到E点距离的范围。
[解析] (1)设光在三棱镜中的折射角为α,则根据折射定律有n=
根据几何关系可得α=30°
代入数据解得sin θ=0.75。
(2)作出单色光线第一次到达半圆弧AMB恰好发生全反射的光路图如图,则由几何关系可知FE上从P点到E点以θ角入射的单色光线第一次到达半圆弧AMB都可以发生全反射,根据全反射临界角公式有sin C=
设P点到FG的距离为l,则根据几何关系有
l=R sin C
又xPE=
联立解得xPE=R
故光线在EF上的入射点D到E点的距离范围为(0,R]。
[答案] (1)0.75 (2)(0,R]
【典例1 教用·备选题】(折射定律的应用)如图所示,在注满水的游泳池的池底有一点光源A,它到池边的水平距离为 3.0 m。 从点光源A射向池边的光线AB与竖直方向的夹角恰好等于全反射的临界角,水的折射率为。
(1)求池内的水深;
(2)一救生员坐在离池边不远处的高凳上,他的眼睛到池面的高度为2.0 m。当他看到正前下方的点光源A时,他的眼睛所接收的光线与竖直方向的夹角恰好为45°。求救生员的眼睛到池边的水平距离(结果保留1位有效数字)。
思路点拨:解此题的关键是根据题意画出光路图,并结合几何关系分析计算。
[解析] (1)光由A射向B恰好发生全反射,光路图如图甲所示
则sin θ=,得sin θ=
又|AO|=3.0 m,由几何关系可得|AB|=4.0 m,|BO|= m,所以水深 m。
(2)光由A点射入救生员眼中的光路图如图乙所示
由折射定律有n=
可知sin α=
则tan α==
设|BE|=x,由几何关系得
tan α==
代入数据得x= m
由几何关系得,救生员到池边的水平距离为 |BC|=(2-x) m≈0.7 m。
[答案] (1) m (2)0.7 m
规律总结 解决光的折射问题的思路
(1)根据题意画出正确的光路图。
(2)利用几何关系确定光路中的边、角关系,要注意入射角、折射角均以法线为标准。
(3)利用折射定律、折射率公式求解。
(4)注意:在折射现象中光路是可逆的。
[典例2] (折射现象的分析)(2024·江苏卷)现有一光线以相同的入射角θ打在不同浓度的两杯NaCl溶液中,折射光线如图所示(β1<β2),已知折射率随浓度增大而变大。则( )
A.甲折射率大 B.甲浓度小
C.甲速度大 D.甲临界角大
√
A [入射角相同,由于β1<β2,根据折射定律可知n甲>n乙,故甲浓度大;根据v=可知光线在甲中的传播速度较小,由sin C=可知折射率越大临界角越小,故甲临界角小。故选A。]
【典例2 教用·备选题】 (折射现象的分析)将一根筷子竖直插入装有水的玻璃杯中,从水平方向拍摄的照片如图所示,看上去浸在水中的这段筷子产生了侧移。下面反映玻璃杯、筷子和照相机位置关系的俯视图可能正确的是( )
A B C D
√
C [如图所示为筷子竖直插入盛水玻璃杯内的俯视图,若A处为筷子(俯视在O点左侧),ABP表示由筷子发出的穿过玻璃杯壁上的B点射向照相机P处的一条光线,ON为过B点沿半径方向的直线,即在B处和空气的分界面的法线,上述光线则相当于在B处由水中射入空气中,图中的角i和角r分别为此光线的入射角和折射角,根据光的折射规律可知,应有r>i,所以照相机在P处拍到的筷子A的像A′的位置不是在A的实际位置,而是由其实际位置偏离杯中心的方向向
杯壁靠拢一些。同理若俯视筷子在O点右侧,则照相机拍到的筷子的像的位置在筷子实际位置的右侧,结合给定的图可知,筷子的像向右偏,则筷子的实际位置在O点右侧。故选C。]
[典例3] (折射率的计算)(2024·重庆卷)某同学设计了一种测量液体折射率的方案。容器过中心轴线的剖面图如图所示,其宽度为
16 cm,让单色光在此剖面内从空气入射到液体表面的中心。调整入射角,当反射光与折射光垂直时,测出竖直器壁上的反射光点与液体表面的距离h,就能得到液体的折射率n。
忽略气壁厚度,由该方案可知( )
A.若h=4 cm,则n=
B.若h=6 cm,则n=
C.若n=,则h=10 cm
D.若n=,则h=5 cm
√
B [根据几何关系画出光路图,如图所示。
标注入射角θ1,折射角θ2,根据折射定律可得n===。若h=4 cm,则n=2,故A错误;若h=6 cm,则n=,故B正确;若n=,则h= cm,故C错误;若n=,则h= cm,故D错误。故选B。]
【典例3 教用·备选题】(折射率的计算)(2021·江苏卷)某种材料制成的半圆形透明砖平放在方格纸上,将激光束垂直于AC面射入,可以看到光束从圆弧面ABC出射,沿AC方向缓慢平移该砖,在如图所示位置时,出射光束恰好消失,该材料的折射率为( )
A.1.2 B.1.4 C.1.6 D.1.8
√
A [画出激光束从玻璃砖射出时恰好发生全反射的入射角,如图所示,全反射的条件是sin θ=,设方格边长为d,由几何关系知sin θ=,联立解得n=1.2,故A正确,B、C、D错误。故选A。]
[典例4] (折射定律与反射定律的综合应用)(2022·江苏卷)如图所示,两条间距为D的平行光线,以入射角θ从空气射入平静水面,反射光线与折射光线垂直,求:
(1)水的折射率n;
(2)两条折射光线之间的距离d。
[解析] (1)设折射角为γ,根据几何关系可得
γ=90°-θ
根据折射定律可得n=
联立可得n=tan θ。
(2)如图所示
根据几何关系可得d=·sin θ=D tan θ。
[答案] (1)tan θ (2)D tan θ
1.分析综合问题的基本思路
(1)判断光线是从光疏介质进入光密介质还是从光密介质进入光疏介质。
(2)判断入射角是否大于等于临界角,明确是否发生全反射现象。
(3)画出反射、折射或全反射的光路图,必要时还可应用光路的可逆原理画出光路图,然后结合几何知识进行推断和求解相关问题。
(4)折射率n是讨论折射和全反射问题的重要物理量,是联系各物理量的桥梁,应熟练掌握跟折射率有关的所有关系式。
考点2 光的折射、全反射的综合
2.求光的传播时间的一般思路
(1)全反射现象中,光在同种均匀介质中的传播速度不发生变化,即v=。
(2)全反射现象中,光的传播路程应结合光路图与几何关系进行确定。
(3)利用t=求解光的传播时间。
[典例5] (全反射现象的应用、光导纤维)(2024·江苏南京一模)如图所示为光导纤维简化为长直玻璃丝的示意图。玻璃丝长度为l。AB、CD分别代表左、右两平行端面。一单色光从AB端面射入玻璃丝。从CD端面射出。已知玻璃丝对单色光的折射率为n(n<)。光在真空中的速度为c。求该单色光:
(1)垂直AB端面入射,在玻璃丝中传
播到CD面的时间t;
(2)能从AB端面传播到另一端面CD。入射角正弦值sin θ的范围。
[解析] (1)单色光在玻璃丝内的传播速度v=,
垂直AB端面入射,在玻璃丝中传播到CD面的时间t==。
(2)如图所示,设光束在玻璃丝端面的入射角为θ,折射角为α,折射光线射向侧面时的入射角为β。要保证光能从另一端面射出,则光能在侧壁发生全反射
根据折射定律n=
根据几何关系α+β=90°,sin α=cos β
则恰好发生全反射时有sin β=
故cos β=
解得sin θ=
要保证从端面射入的光线能在侧壁发生全反射,应有
sin θ≤。
[答案] (1) (2)sin θ≤
【典例5 教用·备选题】 (全反射现象的应用、光导纤维)一光纤通信中信号传播的主要载体是光导纤维,它的结构如图所示,可看成一段直线,其内芯和外套的材料不同,光在内芯中传播,下列关于光导纤维的说法不正确的是( )
A.内芯的折射率比外套的大,光传播时在内芯与外套的界面上发生全反射
B.内芯的折射率比外套的小,光传播时在内芯与外套的界面上发生全反射
C.波长越长的光在光纤中传播的速度越大
D.若紫光以如图所示角度入射时,恰能在光纤中发生全反射,则改用红光以同样角度入射时,不能在光纤中发生全反射
√
B [当内芯的折射率比外套的大时,光传播时在内芯与外套的界面上才能发生全反射,故A正确,B错误;波长越长的光,频率越小,介质对它的折射率n越小,根据公式v=,光在光纤中传播的速度越大,故C正确;根据sin C=知,折射率越大,全反射临界角越小,红光的折射率小,则全反射临界角大,若紫光恰能发生全反射,则红光不能发生全反射,故D正确。]
[典例6] (棱镜的全反射)如图所示,△ABC是一直角三棱镜的横截面,∠A=90°,∠B=60°。一细光束从BC边的D点折射后,射到AC边的E点,发生全反射后经AB边的F点射出。EG垂直于AC交BC于G,D恰好是CG的中点。不计多次反射。
(1)求出射光相对于D点的入射光的偏角;
(2)为实现上述光路,棱镜折射率n的取值应在什么范围内?
思路点拨:(1)根据题设条件,判定光在传播时是否发生全反射,画出入射角等于临界角时的临界光路图。
(2)运用几何关系或三角函数关系以及反射定律等进行分析、判断、运算,从而解决问题。
[解析] (1)光线在BC面上折射,由折射定律有sin i1=n sin r1 ①
式中,n为棱镜的折射率,i1和r1分别是该
光线在BC面上的入射角和折射角。
光线在AC面上发生全反射,由反射定律有
i2=r2 ②
式中i2和r2分别是该光线在AC面上的入射角和反射角
光线在AB面上发生折射,由折射定律有
n sin i3=sin r3 ③
式中i3和r3分别是该光线在AB面上的入射角和折射角
由几何关系得
i2=r2=60°,r1=i3=30° ④
F点的出射光相对于D点的入射光的偏角为
δ=(r1-i1)+(180°-i2-r2)+(r3-i3) ⑤
由①②③④⑤式得
δ=60°。 ⑥
(2)光线在AC面上发生全反射,光线在AB面上不发生全反射,有
n sin i2≥n sin C>n sin i3 ⑦
式中C是全反射临界角,满足
n sin C=1 ⑧
由④⑦⑧式知,棱镜的折射率n的取值范围应为
≤n<2。 ⑨
[答案] (1)60° (2)≤n<2
【典例6 教用·备选题】 (棱镜的全反射)(2024·江苏南京高三开学考试)一直角梯形棱镜ABCD的横截面如图所示,位于截面所在平面内的一束光线由O点垂直AD边射入。已知棱镜的折射率n=1.25,AB=BC=6 cm,OA=1.5 cm,∠DAB=60°,sin 53°=0.8,求:
(1)光线第一次射出棱镜时出射光线的方向;
(2)第一次的出射点距C的距离。
[解析] (1)因为sin C=,所以C=53°,由此可作出光路图如图所示
根据几何关系知α=30°,由=n得sin β=
则出射光线的方向斜向左上方,与水平方向的夹角的正弦值为。
(2)根据几何关系得,AE=EB=BF=FC=3 cm
tan α=
得CG= cm,即第一次的出射点距C的距离为 cm。
[答案] (1)见解析 (2) cm
[典例7] (光的折射和全反射的综合计算)(2025·江苏南通模拟)如图所示,某种材料制成的扇形透明砖放置在水平桌面上,光源S发出一束平行于桌面的光线从OA的中点垂直射入透明砖,恰好经过两次全反射后,垂直OB射出,并再次经过光源S。已知光在真空中传播的速度为c,求:
(1)材料的折射率n;
(2)该过程中,光在空气中传播的时
间与光在材料中传播的时间之比。
[解析] (1)光路如图所示
由折射定律得sin C=
而=,故sin C=(即C=30°)
所以该材料的折射率n=2。
(2)光在空气中传播的路程
s1=2
由几何关系得∠OSF=30°
所以s1=R cos 30°×2=R×2=R,则光在空气中传播的时间为t1==
光在材料中传播的路程s2=4=2R,光在材料中传播的速度v=,则光在材料中传播的时间为t2===
则传播时间之比为t1∶t2=1∶4。
[答案] (1)2 (2)1∶4
【典例7 教用·备选题】 (光的折射和全反射的综合计算)用激光笔照射透明塑料制成的光盘边缘时观察到的现象如图所示。入射点O和两出射点P、Q恰好位于光盘边缘等间隔的三点处,空气中的四条细光束分别为入射光束a、反射光束b、出射光束c和d。已知光束a和b间的夹角为90°,则( )
A.光盘材料的折射率n=2
B.光在光盘内的速度为真空中光速的三分之二
C.光束b、c和d的强度之和等于光束a的强度
D.光束c的强度小于O点处折射光束OP的强度
√
D [依题意作光路图如图所示,由题意可知∠OO′P=120°,可得在O点处的折射角γ=30°,由题意可知α+β=90°,由反射定律得α=β,解得α=β=45°,由折射定律得n===,光在光盘内的速度v==c,即光盘材料的折射率n=,光在光盘内的速度为真空中光速的,故A、B错误;由能量守恒定律可知,若忽略光在传播过程的能量衰减,则光束a的强度应等于光束b、c、d
和e的强度之和,若考虑光在传播过程的能量衰减,则光束a的强度应大于光束b、c、d和e的强度之和,故C错误;在P点处光束OP为入射光束,而光束c和光束PQ分别为折射和反射光束,由能量守恒定律可知,在P点处光束OP的强度等于或大于光束c和光束PQ的强度之和,因此无论是否考虑传播过程中的能量衰减,光束c的强度一定小于O点处折射光束OP的强度,
故D正确。]
1.光的色散
(1)成因:棱镜材料对不同色光的折射率不同,对红光的折射率最小,红光通过棱镜后的偏折程度最小,对紫光的折射率最大,紫光通过棱镜后的偏折程度最大,从而产生色散现象。
考点3 光的色散和光路控制
(2)现象:一束白光通过三棱镜后在屏上会形成彩色光带。
2.平行玻璃砖、三棱镜和圆柱体(球)对光路的控制
平行玻璃砖 三棱镜 圆柱体(球)
结构 玻璃砖上下表面是平行的 横截面为三角形 横截面是圆
对光线的作用 通过平行玻璃砖的光线不改变传播方向,但要发生侧移 通过三棱镜的光线经两次折射后,出射光线向棱镜底边偏折
圆界面的法线是过圆心的直线,经过两次折射后出射光线向圆心偏折
[典例8] (三棱镜的色散)某兴趣小组用单色光a照射图中的三棱镜,观察光在棱镜中的传播情况。ABC为棱镜的截面图,其为底角为30°的等腰三角形,棱镜对单色光a的折射率为。单色光a射入时方向与AB平行,从D点射入,经过折射射向AB的中点E,不考虑光的二次反射,则( )
A.单色光a可能从E点射出AB面
B.改用白光平行于AB、从D射入棱镜,若有光射出BC面,则紫光更靠近B点
C.若入射点D向C移动,光在棱镜中传播的时间不变
D.若入射点D向C移动,光在BC面的出射点上移
√
C [AC面上的入射角为60°,棱镜的折射率为,则==,故AC面上的折射角为β=30°,由几何关系知,光射向E时入射角θ=60°,设光线在E点发生全反射的临界角为C,则有sin C==,由sin CC,可知光线在E点发生全反射,故光不可能从E点射出AB面,故A错误;由于紫光折射率比红光高,如图所示,射出BC面的光中,紫光更靠近C点,故B错误;若入射点D向C移动,由几何关系可知,光束在棱镜中的光程没有发生变化,时间也没有发生变化,故C正确;若入射点D向C移动,光束在AC面上的折射角为30°不发生变化,光线右移在E点右侧,光束在BC面上的入射角不发生变化,光的出射点下移,故D错误。
故选C。]
【典例8 教用·备选题】 (三棱镜的色散)两个完全相同的等腰三棱镜如图所示放置,相邻两侧面相互平行。一束由红光和蓝光组成的复色光从棱镜A的左面入射,从B的右面射出,则出射光线可能正确的是( )
A B
C D
√
B [复色光经两等腰棱镜折射的光路图如图所示,复色光经多次折射,但由于两棱镜相邻两侧面平行,所以各色光出射光线与入射光线平行,最后出射光线是两束平行光。故选B。]
[典例9] (平行玻璃砖的色散)如图所示,一束由两种单色光混合的复色光沿PO方向射向一上、下表面平行的厚玻璃平面镜的上表面,得到三束光Ⅰ、Ⅱ、Ⅲ。下列有关这三束光的判断不正确的是( )
A.光束Ⅰ仍为复色光,光束Ⅱ、Ⅲ为单色光
B.光束Ⅱ在玻璃中的传播速度比光束Ⅲ小
C.增大α角且α<90°,光束Ⅱ、Ⅲ会远离光束Ⅰ
D.改变α角且α<90°,光束Ⅱ、Ⅲ一定与光束Ⅰ平行
√
C [由题意画出如图所示的光路图,可知光束Ⅰ是反射光线,所以仍是复色光,而光束Ⅱ、Ⅲ由于折射率的不同导致偏折分离,所以光束Ⅱ、Ⅲ是单色光,故A正确;由于光束Ⅱ的偏折程度大于光束Ⅲ,所以玻璃对光束Ⅱ的折射率大于对光束Ⅲ的折射率,根据v=可知,光束Ⅱ在玻璃中的传播速度比光束Ⅲ小,故B正确;当增大α角且α<90°,即入射角减小时,光束Ⅱ、Ⅲ会靠近光束Ⅰ,故C错误;因为厚玻璃平面镜的上下表面是平行的,
根据光的入射角与反射角相等以及光的可
逆性,可知改变α角且α<90°,光束Ⅱ、Ⅲ一
定与光束Ⅰ平行,故D正确。]
[典例10] (球形玻璃的色散)虹和霓是太阳光在水柱内分别经过一次和两次反射后出射形成的,可用白光照射玻璃球来说明,两束平行白光照射到透明玻璃球后,在水平的白色桌面上会形成MN和PQ两条彩色光带,光路如图所示,则M、N、P、Q的颜色分别为( )
A.紫、红、红、紫
B.红、紫、红、紫
C.红、紫、紫、红
D.紫、红、紫、红
√
A [白光中含有七种单色光,其中红光的折射率最小,紫光的折射率最大,故进入玻璃球时红光的偏折角最小,紫光的偏折角最大;由玻璃球出来后将形成光带,而两端分别是红光和紫光,根据光路图可知M、Q点为紫光,N、P点为红光,故A正确,B、C、D错误。]
题组一 折射定律和折射率的理解及应用
1.如图所示是一张风景照片,湖水清澈见底,近处湖面水下的景物都看得很清楚,而远处则只看到对岸山峰和天空彩虹的倒影,水面下的景物则根本看不到。
下列说法中正确的是( )
1
题号
2
3
4
5
6
7
8
9
10
11
课时分层作业(三十七) 光的折射 全反射
A.水下的石头看起来的深度比实际深一些
B.可以利用偏振片“过滤”掉山峰和天空彩虹的倒影
C.远处对岸山峰和天空彩虹的倒影十分清晰,是由于光的干涉所引起的
D.远处水面下景物看不到,是因为远处的树木和建筑物反射光强度太大而被覆盖
1
题号
2
3
4
5
6
7
8
9
10
11
√
B [水下石头反射的光线由水中进入空气时,在水面上发生折射,折射角大于入射角,折射光线进入人眼,人眼会逆着折射光线的方向看去,就会觉得石头位置变浅了,所以水下的石头看起来的深度比实际浅一些,故A错误;水面反射的光为偏振光,可利用偏振片“过滤”掉山峰和天空彩虹的倒影,故B正确;远处对岸山峰和天空彩虹的倒影十分清晰,是由于光在水面上发生反射所引起的,故C错误;远处水面下景物的光线射到水面上,入射角很大,当入射角大于等于全反射临界角时能发生全反射,光线不能射出水面,因而看不见,故D错误。故选B。]
1
题号
2
3
4
5
6
7
8
9
10
11
2.(2023·江苏卷)地球表面附近空气的折射率随高度降低而增大,太阳光斜射向地面的过程中会发生弯曲。下列光路图中能描述该现象的是( )
1
题号
2
3
4
5
6
7
8
9
10
11
A B C D
√
A [光由光疏介质射入光密介质时,折射角小于入射角,又由题意可知,地球表面附近空气的折射率随高度降低而增大,则太阳光应向下弯曲,A正确,B、C、D错误。]
1
题号
2
3
4
5
6
7
8
9
10
11
3.(2021·江苏新高考适应性考试)如图所示,一束激光照射在横截面为正方形的透明玻璃柱上,光线与横截面平行,则透过玻璃柱的光线可能是图中的( )
A.①
B.②
C.③
D.④
1
题号
2
3
4
5
6
7
8
9
10
11
√
C [作出光路图,如图所示,根据折射定律有n=,n>1,解得i1>r1,所以折射光线向右偏折;根据折射定律有n=,由几何知识可知r1=r2,解得i1=i2,所以出
射光线与入射光线平行。故选C。]
1
题号
2
3
4
5
6
7
8
9
10
11
4.(2024·贵州卷)一种测量液体折射率的V形容器由两块材质相同的直角棱镜粘合,并封闭其前后两端制作而成。容器中盛有某种液体,一激光束从左边棱镜水平射入,通过液体后从右边棱镜射出,其光路如图所示。设棱镜和液体的折射率分别为n0、n,光在棱镜和液体中的传播速度分别为v0、v,
则( )
A.nv0
B.nC.n>n0,v>v0
D.n>n0,v1
题号
2
3
4
5
6
7
8
9
10
11
√
A [由题图可知光从棱镜进入液体中时,入射角小于折射角,根据折射定律可知nv0。故选A。]
1
题号
2
3
4
5
6
7
8
9
10
11
题组二 全反射现象的理解和应用
5.光的反射、折射及全反射是自然界中很常见的现象,在一次实验课上,某小组进行了实验:将一束单色细光束由空气(视为真空)沿着半径方向射入一块半圆柱形透明体,如图甲所示,对其从圆心O点射出后的折射光线的强度用相应传感器进行了记录,发现从O点射出的折射光线的强度随着夹角θ的变化而变化,变化情况如图乙的图线所示,则下列说法正确的是( )
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
A.当夹角θ小于30°时,在O点处既有反射光,又有折射光
B.圆柱形透明体对该单色光的全反射临界角为30°
C.圆柱形透明体对该单色光的折射率为2
D.圆柱形透明体对该单色光的折射率为
√
D [从题图乙中可以看出,当夹角θ小于30°时,没有折射光,A错误;当θ=30°,即入射角为60°时,折射光线的强度为零,故此时发生全反射,临界角为60°,B错误;因为全反射临界角为60°,所以n==,C错误,D正确。]
1
题号
2
3
4
5
6
7
8
9
10
11
6.由于大气层的存在,太阳光线在大气中折射,使得太阳“落山”后我们仍然能看见它。某同学为研究这一现象,建立了简化模型。将折射率很小的不均匀大气等效成折射率为的均匀大气,并将大气层的厚度等效为地球半径R。根据此模型,一个住在赤道上的人一天中能看到太阳的时长为( )
A.12小时
B.13小时
C.14小时
D.15小时
1
题号
2
3
4
5
6
7
8
9
10
11
√
C [太阳光是平行光,临界光路图如图所示,由几何关系可得临界光线的折射角满足sin r==,可知临界光线的折射角为30°,根据折射定律可得n==,解得i=45°,由几何关系可知,地球多转α角度便看不见太阳了,有α=60°-45°=15°,一个住在赤道上的人在太阳“落山”后还能看到太阳的时间为t=×24 h=1 h,同理可知,在太阳升起时也能提早一小时看到太阳,则一个住在赤道上的人一天中能看到太阳的时长为14 h。
故选C。]
1
题号
2
3
4
5
6
7
8
9
10
11
题组三 折射定律和全反射现象的综合应用
7.(2024·江苏宿迁一模)右图是某种新型光导纤维材料的一小段,材料呈圆柱状,其中MQ为直径,一束单色光以入射角α从空气射向圆心O,下列说法正确的是( )
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
A.光纤通信应用了光的衍射
B.单色光从MQ射入光导纤维时,折射角大于入射角
C.若α=45°时,单色光刚好不从MN射出,则光导纤维的折射率为
D.若光导纤维的折射率为2,则无论入射角α多大,单色光都不会从MN或QP射出
√
D [光纤通信应用了光的全反射,故A错误;单色光从MQ射入光导纤维时,即从光疏介质进入光密介质,折射角小于入射角,故B错误;若α=45°时,单色光刚好不从MN射出,光路图如图甲所示。
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
根据折射定律有n=,临界角满足sin C=,根据几何关系有C+r=90°,则光导纤维的折射率为n=,故C错误;无论入射角α为多少,单色光都不会从MN或QP射出,光导纤维的折射率最小时,光路图如图乙所示。
1
题号
2
3
4
5
6
7
8
9
10
11
根据折射定律有n′=,临界角为sin C′=,根据几何关系有C′+r′=90°,则光导纤维的折射率最小值为n′=<2,故若光导纤维的折射率为2,则无论入射角α为多少,单色光都不会从MN或QP射出,故D正确。故选D。]
8.冰雕展上,厚厚的冰墙内安装有LED光源S,冰墙表面平整而光滑,光源可视为点光源。小明想测量光源到墙面的距离h及冰的折射率n,设计了如下实验:如图(a)所示,将半径为R的圆形纸片贴在墙面上,圆心正对光源。用白纸板做屏,平行墙面从纸片处向后移动,当屏上黑影的半径等于2R时,测出屏到墙面的距离d,换用不同半径的纸片重复上述实验,得到多组数据,在坐标纸上画出d2-R2图像如图(b)所示,直线横截距为a,纵截距为b,则下列说法正确的是( )
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
A.光源到墙面的距离为
B.光源到墙面的距离为
C.冰的折射率为
D.冰的折射率为
√
A [如图所示,设到达圆形纸片边缘的光的入射角为r,折射角i,则由几何关系及折射定律可得n=,sin i=,sin r=,联立可得d2=R2+,结合题图(b)可得-1=-=b,所以h=,n=,故选A。]
1
题号
2
3
4
5
6
7
8
9
10
11
9.(2024·全国甲卷)一玻璃柱的折射率n=,其横截面为四分之一圆,圆的半径为R,如图所示。截面所在平面内,一束与AB边平行的光线从圆弧入射。入射光线与AB边的距离由小变大,距离为h时,光线进入柱体后射到BC边恰好发生全反射。求此时h与R的比值。
1
题号
2
3
4
5
6
7
8
9
10
11
[解析] 根据题意可画出入射光线与AB边的距离为h时的光路图,如图所示
由折射定律有n==
由全反射临界角公式有sin C0=
由几何关系有i=r+C0
h=R sin i
联立解得=。
1
题号
2
3
4
5
6
7
8
9
10
11
[答案]
10.(2024·江苏南京师大附中模拟)反光膜是一种广泛用于道路交通标志的材料,基本结构如图所示。光照射到反光膜的玻璃珠上时,经折射后射到反射层反射,最终平行于原入射方向反向射出玻璃珠。玻璃珠是半径为R的均匀球体,AB是入射光线,其出射光线与光线AB的间距为R。
1
题号
2
3
4
5
6
7
8
9
10
11
(1)请作出光线AB从射入到射出玻璃珠的完整光路图;
(2)求玻璃珠的折射率n。
1
题号
2
3
4
5
6
7
8
9
10
11
[解析] (1)光路图如图所示。
(2)设射入B点光线的入射角为θ1,折射角为θ2,则sin θ1==,则θ1=60°
由几何知识知θ1=2θ2,则θ2=30°
由折射定律有n=
解得n=。
1
题号
2
3
4
5
6
7
8
9
10
11
[答案] (1)见解析图 (2)
11.如图所示,透明玻璃体的上半部分是半球体,下半部分是圆柱体,半球体的半径为R,O为半球体的球心。圆柱体的底面半径和高也为R,现有一半径为R的圆环形平行光垂直于圆柱体底面射向半球体,OO1为圆光环的中心轴线,所有光线经折射后恰好经过圆柱体下表面圆心O1点,光线从O1射出后在玻璃体下方的水平光屏上形成圆形亮环,光到圆柱体底面的距离为R,光在真空中的传播速度为c。求:
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
(1)透明玻璃体的折射率;
(2)光从入射点传播到光屏所用的时间。
[解析] (1)作出光路图如图所示,设光线的入射角为α,折射角为β,则
由几何关系可得
R sin α=R
解得α=60°
由图可知α=2β
所以β=30°
由折射定律可知n==。
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
(2)光在透明玻璃体中的传播速度为v=
光在透明玻璃体中的传播时间为t1==
由图及折射定律知光线从O1点射出后与竖直方向的夹角为α=60°
所以光从透明玻璃体射出后到光屏所用的时间为t2==
则光从入射点传播到光屏所用的时间为t=t1+t2=。
[答案] (1) (2)
谢 谢 !
第十三章 光 电磁波
第十三章 光 电磁波
知能模块 考点内容 高考(江苏卷)六年命题情况对照分析
2019-2024 命题分析
第1节 光的折射 全反射 光的折射 2019T13(3):光的全反射、临界角 2020T13(2):全反射 2021适应考T2:光的折射 2021T7:光的折射 2022T12:光的折射 2023T5:光的折射 高考对本章的考查以计算题为主,有时也会考选择题和填空题。考查的重点是光的折射定律、光的全反射的综合应用。
全反射
第十三章 光 电磁波
知能模块 考点内容 高考(江苏卷)六年命题情况对照分析
2019-2024 命题分析
第2节 光的波动性 电磁波 光的干涉 2020T13(1)(3):电磁波的应用、电磁波波长与频率的关系 2021适应考T1:光的偏振 2021T6:光的干涉 2023T6:光的干涉 2024T2:光的偏振 2024T6:光的折射 高考对本章的考查以计算题为主,有时也会考选择题和填空题。考查的重点是光的折射定律、光的全反射的综合应用。
光的衍射
光的偏振、激光
电磁振荡
第十三章 光 电磁波
知能模块 考点内容 高考(江苏卷)六年命题情况对照分析
2019-2024 命题分析
第2节 光的波动性 电磁波 电磁场与电磁波 2020T13(1)(3):电磁波的应用、电磁波波长与频率的关系 2021适应考T1:光的偏振 2021T6:光的干涉 2023T6:光的干涉 2024T2:光的偏振 2024T6:光的折射 高考对本章的考查以计算题为主,有时也会考选择题和填空题。考查的重点是光的折射定律、光的全反射的综合应用。
无线电波的发射与接收
电磁波谱
实验十八 测量玻璃的折射率
实验十九 用双缝干涉实验测量光的波长
第1节
光的折射 全反射
链接教材·夯基固本
一、光的折射定律 折射率
1.折射现象
光从一种介质____入另一种介质时传播方向发生____的现象,如图所示(以光从空气射入水中为例)。
斜射
改变
2.折射定律
(1)内容:折射光线与入射光线、法线处在________内,折射光线与入射光线分别位于法线的____;入射角的正弦与折射角的正弦成__比。
(2)表达式:=n。
[温馨提示] ①在光的折射现象中,光路是可逆的。
②当光从真空(或空气)斜射入某种介质时,入射角大于折射角;当光由介质斜射入真空(或空气)时,入射角小于折射角。
同一平面
两侧
正
3.折射率
(1)折射率是反映介质的____性质的物理量。
(2)定义式:n=。
(3)计算式:n=,因为v
(1)折射率由________性质决定,与入射角的大小____。
(2)折射率与介质的____没有关系,光密介质不是指密度大的介质。
(3)同一种介质中,频率越大的色光折射率越__,传播速度越__。
光学
大于
介质本身
无关
密度
大
小
二、全反射
1.定义:光从光密介质射入____介质,当入射角增大到某一角度时,折射光线全部____,只剩下反射光线的现象。
2.条件
(1)光从光密介质射入____介质。
(2)入射角__________临界角。
光疏
消失
光疏
大于或等于
3.临界角
(1)定义:折射角等于____时的入射角。
(2)公式:sin C=。若光从光密介质(折射率为n)射向真空或空气时,发生全反射的临界角为C,由n=得sin C=。
(3)大小:介质的折射率n越大,发生全反射的临界角C越__。
90°
小
4.光导纤维
光导纤维的原理是利用光的______,如图所示。
全反射
三、光的色散
1.光的色散现象:含有多种颜色的光被分解为单色光的现象。
2.光谱:含有多种颜色的光被分解后,各种色光按其波长有序排列。
3.光的色散现象说明
(1)白光为复色光;
(2)同一介质对不同色光的折射率不同,频率越大的色光折射率____;
(3)不同色光在同一介质中的传播速度不同,波长越短,波速____。
越大
越慢
一、易错易误辨析(正确的打“√”,错误的打“×”)
(1)某种玻璃对蓝光的折射率比红光大,蓝光和红光以相同的入射角从空气斜射入该玻璃中,蓝光的折射角较大。 ( )
(2)在水中,蓝光的传播速度大于红光的传播速度。 ( )
(3)在潜水员看来,岸上的所有景物都出现在一个倒立的圆锥里。 ( )
×
×
√
(4)光从空气射入玻璃时,只要入射角足够大就可能发生全反射。 ( )
(5)光纤通信利用了全反射的原理。 ( )
(6)晚上,在池水中同一深度的两点光源分别发出红光和蓝光,水面上的人看蓝光光源浅一些。 ( )
×
√
√
二、教材习题衍生
1.(光的折射)有一正三角形OPQ玻璃砖,某束光线垂直于OP射入,恰好在PQ界面发生全反射,则玻璃砖的折射率( )
A. B. C. D.2
√
C [光路图如图所示,根据几何关系可知光线在PQ界面的入射角为C=60°,根据全反射的临界条件可得 sin C=,解得n=。故选C。]
2.(光的全反射的应用)如图所示是一个用折射率n=2.4的透明介质做成的四棱柱的横截面图,其中∠A=∠C=90°,∠B=60°,现有一束光从图示的位置垂直入射到棱镜的AB面上。(注意:每个面的反射光线和折射光线都不能忽略)则
以下说法正确的是( )
A.入射光有可能从DC边射出
B.入射光有可能从AB边射出
C.入射光不可能从BC边垂直射出
D.入射光从BC边垂直射出
√
细研考点·突破题型
1.对折射率的理解
(1)公式n=中,不论光是从真空射入介质,还是从介质射入真空,θ1总是真空中的光线与法线间的夹角,θ2总是介质中的光线与法线间的夹角。
(2)折射率的大小不仅反映了介质对光的折射本领,也反映了光在介质中传播速度的大小,v=。
考点1 折射定律和折射率的理解及应用
(3)折射率与入射角的大小无关,与介质的密度无关,光密介质不是指密度大的介质。
(4)折射率的大小不仅与介质本身有关,还与光的频率有关。同一种介质中,频率越大的色光折射率越大,传播速度越小。
(5)同一种色光,在不同介质中虽然波速、波长不同,但频率不变。
2.光路的可逆性:在光的折射现象中,光路是可逆的。如果让光线逆着原来的折射光线射到界面上,光线就会逆着原来的入射光线发生折射。
[典例1] (折射定律的应用)(2024·山东卷)某光学组件横截面如图所示,半圆形玻璃砖圆心为O点,半径为R;直角三棱镜FG边的延长线过O点,EG边平行于AB边且长度等于R,∠FEG=30°。横截面所在平面内,单色光线以θ角入射到EF边发生折射,折射光线垂直EG边射出。已知玻璃砖和三棱镜对
该单色光的折射率均为1.5。
(1)求sin θ;
(2)以θ角入射的单色光线,若第一次到达半圆弧AMB可以发生全反射,求光线在EF上入射点D(图中未标出)到E点距离的范围。
[解析] (1)设光在三棱镜中的折射角为α,则根据折射定律有n=
根据几何关系可得α=30°
代入数据解得sin θ=0.75。
(2)作出单色光线第一次到达半圆弧AMB恰好发生全反射的光路图如图,则由几何关系可知FE上从P点到E点以θ角入射的单色光线第一次到达半圆弧AMB都可以发生全反射,根据全反射临界角公式有sin C=
设P点到FG的距离为l,则根据几何关系有
l=R sin C
又xPE=
联立解得xPE=R
故光线在EF上的入射点D到E点的距离范围为(0,R]。
[答案] (1)0.75 (2)(0,R]
【典例1 教用·备选题】(折射定律的应用)如图所示,在注满水的游泳池的池底有一点光源A,它到池边的水平距离为 3.0 m。 从点光源A射向池边的光线AB与竖直方向的夹角恰好等于全反射的临界角,水的折射率为。
(1)求池内的水深;
(2)一救生员坐在离池边不远处的高凳上,他的眼睛到池面的高度为2.0 m。当他看到正前下方的点光源A时,他的眼睛所接收的光线与竖直方向的夹角恰好为45°。求救生员的眼睛到池边的水平距离(结果保留1位有效数字)。
思路点拨:解此题的关键是根据题意画出光路图,并结合几何关系分析计算。
[解析] (1)光由A射向B恰好发生全反射,光路图如图甲所示
则sin θ=,得sin θ=
又|AO|=3.0 m,由几何关系可得|AB|=4.0 m,|BO|= m,所以水深 m。
(2)光由A点射入救生员眼中的光路图如图乙所示
由折射定律有n=
可知sin α=
则tan α==
设|BE|=x,由几何关系得
tan α==
代入数据得x= m
由几何关系得,救生员到池边的水平距离为 |BC|=(2-x) m≈0.7 m。
[答案] (1) m (2)0.7 m
规律总结 解决光的折射问题的思路
(1)根据题意画出正确的光路图。
(2)利用几何关系确定光路中的边、角关系,要注意入射角、折射角均以法线为标准。
(3)利用折射定律、折射率公式求解。
(4)注意:在折射现象中光路是可逆的。
[典例2] (折射现象的分析)(2024·江苏卷)现有一光线以相同的入射角θ打在不同浓度的两杯NaCl溶液中,折射光线如图所示(β1<β2),已知折射率随浓度增大而变大。则( )
A.甲折射率大 B.甲浓度小
C.甲速度大 D.甲临界角大
√
A [入射角相同,由于β1<β2,根据折射定律可知n甲>n乙,故甲浓度大;根据v=可知光线在甲中的传播速度较小,由sin C=可知折射率越大临界角越小,故甲临界角小。故选A。]
【典例2 教用·备选题】 (折射现象的分析)将一根筷子竖直插入装有水的玻璃杯中,从水平方向拍摄的照片如图所示,看上去浸在水中的这段筷子产生了侧移。下面反映玻璃杯、筷子和照相机位置关系的俯视图可能正确的是( )
A B C D
√
C [如图所示为筷子竖直插入盛水玻璃杯内的俯视图,若A处为筷子(俯视在O点左侧),ABP表示由筷子发出的穿过玻璃杯壁上的B点射向照相机P处的一条光线,ON为过B点沿半径方向的直线,即在B处和空气的分界面的法线,上述光线则相当于在B处由水中射入空气中,图中的角i和角r分别为此光线的入射角和折射角,根据光的折射规律可知,应有r>i,所以照相机在P处拍到的筷子A的像A′的位置不是在A的实际位置,而是由其实际位置偏离杯中心的方向向
杯壁靠拢一些。同理若俯视筷子在O点右侧,则照相机拍到的筷子的像的位置在筷子实际位置的右侧,结合给定的图可知,筷子的像向右偏,则筷子的实际位置在O点右侧。故选C。]
[典例3] (折射率的计算)(2024·重庆卷)某同学设计了一种测量液体折射率的方案。容器过中心轴线的剖面图如图所示,其宽度为
16 cm,让单色光在此剖面内从空气入射到液体表面的中心。调整入射角,当反射光与折射光垂直时,测出竖直器壁上的反射光点与液体表面的距离h,就能得到液体的折射率n。
忽略气壁厚度,由该方案可知( )
A.若h=4 cm,则n=
B.若h=6 cm,则n=
C.若n=,则h=10 cm
D.若n=,则h=5 cm
√
B [根据几何关系画出光路图,如图所示。
标注入射角θ1,折射角θ2,根据折射定律可得n===。若h=4 cm,则n=2,故A错误;若h=6 cm,则n=,故B正确;若n=,则h= cm,故C错误;若n=,则h= cm,故D错误。故选B。]
【典例3 教用·备选题】(折射率的计算)(2021·江苏卷)某种材料制成的半圆形透明砖平放在方格纸上,将激光束垂直于AC面射入,可以看到光束从圆弧面ABC出射,沿AC方向缓慢平移该砖,在如图所示位置时,出射光束恰好消失,该材料的折射率为( )
A.1.2 B.1.4 C.1.6 D.1.8
√
A [画出激光束从玻璃砖射出时恰好发生全反射的入射角,如图所示,全反射的条件是sin θ=,设方格边长为d,由几何关系知sin θ=,联立解得n=1.2,故A正确,B、C、D错误。故选A。]
[典例4] (折射定律与反射定律的综合应用)(2022·江苏卷)如图所示,两条间距为D的平行光线,以入射角θ从空气射入平静水面,反射光线与折射光线垂直,求:
(1)水的折射率n;
(2)两条折射光线之间的距离d。
[解析] (1)设折射角为γ,根据几何关系可得
γ=90°-θ
根据折射定律可得n=
联立可得n=tan θ。
(2)如图所示
根据几何关系可得d=·sin θ=D tan θ。
[答案] (1)tan θ (2)D tan θ
1.分析综合问题的基本思路
(1)判断光线是从光疏介质进入光密介质还是从光密介质进入光疏介质。
(2)判断入射角是否大于等于临界角,明确是否发生全反射现象。
(3)画出反射、折射或全反射的光路图,必要时还可应用光路的可逆原理画出光路图,然后结合几何知识进行推断和求解相关问题。
(4)折射率n是讨论折射和全反射问题的重要物理量,是联系各物理量的桥梁,应熟练掌握跟折射率有关的所有关系式。
考点2 光的折射、全反射的综合
2.求光的传播时间的一般思路
(1)全反射现象中,光在同种均匀介质中的传播速度不发生变化,即v=。
(2)全反射现象中,光的传播路程应结合光路图与几何关系进行确定。
(3)利用t=求解光的传播时间。
[典例5] (全反射现象的应用、光导纤维)(2024·江苏南京一模)如图所示为光导纤维简化为长直玻璃丝的示意图。玻璃丝长度为l。AB、CD分别代表左、右两平行端面。一单色光从AB端面射入玻璃丝。从CD端面射出。已知玻璃丝对单色光的折射率为n(n<)。光在真空中的速度为c。求该单色光:
(1)垂直AB端面入射,在玻璃丝中传
播到CD面的时间t;
(2)能从AB端面传播到另一端面CD。入射角正弦值sin θ的范围。
[解析] (1)单色光在玻璃丝内的传播速度v=,
垂直AB端面入射,在玻璃丝中传播到CD面的时间t==。
(2)如图所示,设光束在玻璃丝端面的入射角为θ,折射角为α,折射光线射向侧面时的入射角为β。要保证光能从另一端面射出,则光能在侧壁发生全反射
根据折射定律n=
根据几何关系α+β=90°,sin α=cos β
则恰好发生全反射时有sin β=
故cos β=
解得sin θ=
要保证从端面射入的光线能在侧壁发生全反射,应有
sin θ≤。
[答案] (1) (2)sin θ≤
【典例5 教用·备选题】 (全反射现象的应用、光导纤维)一光纤通信中信号传播的主要载体是光导纤维,它的结构如图所示,可看成一段直线,其内芯和外套的材料不同,光在内芯中传播,下列关于光导纤维的说法不正确的是( )
A.内芯的折射率比外套的大,光传播时在内芯与外套的界面上发生全反射
B.内芯的折射率比外套的小,光传播时在内芯与外套的界面上发生全反射
C.波长越长的光在光纤中传播的速度越大
D.若紫光以如图所示角度入射时,恰能在光纤中发生全反射,则改用红光以同样角度入射时,不能在光纤中发生全反射
√
B [当内芯的折射率比外套的大时,光传播时在内芯与外套的界面上才能发生全反射,故A正确,B错误;波长越长的光,频率越小,介质对它的折射率n越小,根据公式v=,光在光纤中传播的速度越大,故C正确;根据sin C=知,折射率越大,全反射临界角越小,红光的折射率小,则全反射临界角大,若紫光恰能发生全反射,则红光不能发生全反射,故D正确。]
[典例6] (棱镜的全反射)如图所示,△ABC是一直角三棱镜的横截面,∠A=90°,∠B=60°。一细光束从BC边的D点折射后,射到AC边的E点,发生全反射后经AB边的F点射出。EG垂直于AC交BC于G,D恰好是CG的中点。不计多次反射。
(1)求出射光相对于D点的入射光的偏角;
(2)为实现上述光路,棱镜折射率n的取值应在什么范围内?
思路点拨:(1)根据题设条件,判定光在传播时是否发生全反射,画出入射角等于临界角时的临界光路图。
(2)运用几何关系或三角函数关系以及反射定律等进行分析、判断、运算,从而解决问题。
[解析] (1)光线在BC面上折射,由折射定律有sin i1=n sin r1 ①
式中,n为棱镜的折射率,i1和r1分别是该
光线在BC面上的入射角和折射角。
光线在AC面上发生全反射,由反射定律有
i2=r2 ②
式中i2和r2分别是该光线在AC面上的入射角和反射角
光线在AB面上发生折射,由折射定律有
n sin i3=sin r3 ③
式中i3和r3分别是该光线在AB面上的入射角和折射角
由几何关系得
i2=r2=60°,r1=i3=30° ④
F点的出射光相对于D点的入射光的偏角为
δ=(r1-i1)+(180°-i2-r2)+(r3-i3) ⑤
由①②③④⑤式得
δ=60°。 ⑥
(2)光线在AC面上发生全反射,光线在AB面上不发生全反射,有
n sin i2≥n sin C>n sin i3 ⑦
式中C是全反射临界角,满足
n sin C=1 ⑧
由④⑦⑧式知,棱镜的折射率n的取值范围应为
≤n<2。 ⑨
[答案] (1)60° (2)≤n<2
【典例6 教用·备选题】 (棱镜的全反射)(2024·江苏南京高三开学考试)一直角梯形棱镜ABCD的横截面如图所示,位于截面所在平面内的一束光线由O点垂直AD边射入。已知棱镜的折射率n=1.25,AB=BC=6 cm,OA=1.5 cm,∠DAB=60°,sin 53°=0.8,求:
(1)光线第一次射出棱镜时出射光线的方向;
(2)第一次的出射点距C的距离。
[解析] (1)因为sin C=,所以C=53°,由此可作出光路图如图所示
根据几何关系知α=30°,由=n得sin β=
则出射光线的方向斜向左上方,与水平方向的夹角的正弦值为。
(2)根据几何关系得,AE=EB=BF=FC=3 cm
tan α=
得CG= cm,即第一次的出射点距C的距离为 cm。
[答案] (1)见解析 (2) cm
[典例7] (光的折射和全反射的综合计算)(2025·江苏南通模拟)如图所示,某种材料制成的扇形透明砖放置在水平桌面上,光源S发出一束平行于桌面的光线从OA的中点垂直射入透明砖,恰好经过两次全反射后,垂直OB射出,并再次经过光源S。已知光在真空中传播的速度为c,求:
(1)材料的折射率n;
(2)该过程中,光在空气中传播的时
间与光在材料中传播的时间之比。
[解析] (1)光路如图所示
由折射定律得sin C=
而=,故sin C=(即C=30°)
所以该材料的折射率n=2。
(2)光在空气中传播的路程
s1=2
由几何关系得∠OSF=30°
所以s1=R cos 30°×2=R×2=R,则光在空气中传播的时间为t1==
光在材料中传播的路程s2=4=2R,光在材料中传播的速度v=,则光在材料中传播的时间为t2===
则传播时间之比为t1∶t2=1∶4。
[答案] (1)2 (2)1∶4
【典例7 教用·备选题】 (光的折射和全反射的综合计算)用激光笔照射透明塑料制成的光盘边缘时观察到的现象如图所示。入射点O和两出射点P、Q恰好位于光盘边缘等间隔的三点处,空气中的四条细光束分别为入射光束a、反射光束b、出射光束c和d。已知光束a和b间的夹角为90°,则( )
A.光盘材料的折射率n=2
B.光在光盘内的速度为真空中光速的三分之二
C.光束b、c和d的强度之和等于光束a的强度
D.光束c的强度小于O点处折射光束OP的强度
√
D [依题意作光路图如图所示,由题意可知∠OO′P=120°,可得在O点处的折射角γ=30°,由题意可知α+β=90°,由反射定律得α=β,解得α=β=45°,由折射定律得n===,光在光盘内的速度v==c,即光盘材料的折射率n=,光在光盘内的速度为真空中光速的,故A、B错误;由能量守恒定律可知,若忽略光在传播过程的能量衰减,则光束a的强度应等于光束b、c、d
和e的强度之和,若考虑光在传播过程的能量衰减,则光束a的强度应大于光束b、c、d和e的强度之和,故C错误;在P点处光束OP为入射光束,而光束c和光束PQ分别为折射和反射光束,由能量守恒定律可知,在P点处光束OP的强度等于或大于光束c和光束PQ的强度之和,因此无论是否考虑传播过程中的能量衰减,光束c的强度一定小于O点处折射光束OP的强度,
故D正确。]
1.光的色散
(1)成因:棱镜材料对不同色光的折射率不同,对红光的折射率最小,红光通过棱镜后的偏折程度最小,对紫光的折射率最大,紫光通过棱镜后的偏折程度最大,从而产生色散现象。
考点3 光的色散和光路控制
(2)现象:一束白光通过三棱镜后在屏上会形成彩色光带。
2.平行玻璃砖、三棱镜和圆柱体(球)对光路的控制
平行玻璃砖 三棱镜 圆柱体(球)
结构 玻璃砖上下表面是平行的 横截面为三角形 横截面是圆
对光线的作用 通过平行玻璃砖的光线不改变传播方向,但要发生侧移 通过三棱镜的光线经两次折射后,出射光线向棱镜底边偏折
圆界面的法线是过圆心的直线,经过两次折射后出射光线向圆心偏折
[典例8] (三棱镜的色散)某兴趣小组用单色光a照射图中的三棱镜,观察光在棱镜中的传播情况。ABC为棱镜的截面图,其为底角为30°的等腰三角形,棱镜对单色光a的折射率为。单色光a射入时方向与AB平行,从D点射入,经过折射射向AB的中点E,不考虑光的二次反射,则( )
A.单色光a可能从E点射出AB面
B.改用白光平行于AB、从D射入棱镜,若有光射出BC面,则紫光更靠近B点
C.若入射点D向C移动,光在棱镜中传播的时间不变
D.若入射点D向C移动,光在BC面的出射点上移
√
C [AC面上的入射角为60°,棱镜的折射率为,则==,故AC面上的折射角为β=30°,由几何关系知,光射向E时入射角θ=60°,设光线在E点发生全反射的临界角为C,则有sin C==,由sin C
故选C。]
【典例8 教用·备选题】 (三棱镜的色散)两个完全相同的等腰三棱镜如图所示放置,相邻两侧面相互平行。一束由红光和蓝光组成的复色光从棱镜A的左面入射,从B的右面射出,则出射光线可能正确的是( )
A B
C D
√
B [复色光经两等腰棱镜折射的光路图如图所示,复色光经多次折射,但由于两棱镜相邻两侧面平行,所以各色光出射光线与入射光线平行,最后出射光线是两束平行光。故选B。]
[典例9] (平行玻璃砖的色散)如图所示,一束由两种单色光混合的复色光沿PO方向射向一上、下表面平行的厚玻璃平面镜的上表面,得到三束光Ⅰ、Ⅱ、Ⅲ。下列有关这三束光的判断不正确的是( )
A.光束Ⅰ仍为复色光,光束Ⅱ、Ⅲ为单色光
B.光束Ⅱ在玻璃中的传播速度比光束Ⅲ小
C.增大α角且α<90°,光束Ⅱ、Ⅲ会远离光束Ⅰ
D.改变α角且α<90°,光束Ⅱ、Ⅲ一定与光束Ⅰ平行
√
C [由题意画出如图所示的光路图,可知光束Ⅰ是反射光线,所以仍是复色光,而光束Ⅱ、Ⅲ由于折射率的不同导致偏折分离,所以光束Ⅱ、Ⅲ是单色光,故A正确;由于光束Ⅱ的偏折程度大于光束Ⅲ,所以玻璃对光束Ⅱ的折射率大于对光束Ⅲ的折射率,根据v=可知,光束Ⅱ在玻璃中的传播速度比光束Ⅲ小,故B正确;当增大α角且α<90°,即入射角减小时,光束Ⅱ、Ⅲ会靠近光束Ⅰ,故C错误;因为厚玻璃平面镜的上下表面是平行的,
根据光的入射角与反射角相等以及光的可
逆性,可知改变α角且α<90°,光束Ⅱ、Ⅲ一
定与光束Ⅰ平行,故D正确。]
[典例10] (球形玻璃的色散)虹和霓是太阳光在水柱内分别经过一次和两次反射后出射形成的,可用白光照射玻璃球来说明,两束平行白光照射到透明玻璃球后,在水平的白色桌面上会形成MN和PQ两条彩色光带,光路如图所示,则M、N、P、Q的颜色分别为( )
A.紫、红、红、紫
B.红、紫、红、紫
C.红、紫、紫、红
D.紫、红、紫、红
√
A [白光中含有七种单色光,其中红光的折射率最小,紫光的折射率最大,故进入玻璃球时红光的偏折角最小,紫光的偏折角最大;由玻璃球出来后将形成光带,而两端分别是红光和紫光,根据光路图可知M、Q点为紫光,N、P点为红光,故A正确,B、C、D错误。]
题组一 折射定律和折射率的理解及应用
1.如图所示是一张风景照片,湖水清澈见底,近处湖面水下的景物都看得很清楚,而远处则只看到对岸山峰和天空彩虹的倒影,水面下的景物则根本看不到。
下列说法中正确的是( )
1
题号
2
3
4
5
6
7
8
9
10
11
课时分层作业(三十七) 光的折射 全反射
A.水下的石头看起来的深度比实际深一些
B.可以利用偏振片“过滤”掉山峰和天空彩虹的倒影
C.远处对岸山峰和天空彩虹的倒影十分清晰,是由于光的干涉所引起的
D.远处水面下景物看不到,是因为远处的树木和建筑物反射光强度太大而被覆盖
1
题号
2
3
4
5
6
7
8
9
10
11
√
B [水下石头反射的光线由水中进入空气时,在水面上发生折射,折射角大于入射角,折射光线进入人眼,人眼会逆着折射光线的方向看去,就会觉得石头位置变浅了,所以水下的石头看起来的深度比实际浅一些,故A错误;水面反射的光为偏振光,可利用偏振片“过滤”掉山峰和天空彩虹的倒影,故B正确;远处对岸山峰和天空彩虹的倒影十分清晰,是由于光在水面上发生反射所引起的,故C错误;远处水面下景物的光线射到水面上,入射角很大,当入射角大于等于全反射临界角时能发生全反射,光线不能射出水面,因而看不见,故D错误。故选B。]
1
题号
2
3
4
5
6
7
8
9
10
11
2.(2023·江苏卷)地球表面附近空气的折射率随高度降低而增大,太阳光斜射向地面的过程中会发生弯曲。下列光路图中能描述该现象的是( )
1
题号
2
3
4
5
6
7
8
9
10
11
A B C D
√
A [光由光疏介质射入光密介质时,折射角小于入射角,又由题意可知,地球表面附近空气的折射率随高度降低而增大,则太阳光应向下弯曲,A正确,B、C、D错误。]
1
题号
2
3
4
5
6
7
8
9
10
11
3.(2021·江苏新高考适应性考试)如图所示,一束激光照射在横截面为正方形的透明玻璃柱上,光线与横截面平行,则透过玻璃柱的光线可能是图中的( )
A.①
B.②
C.③
D.④
1
题号
2
3
4
5
6
7
8
9
10
11
√
C [作出光路图,如图所示,根据折射定律有n=,n>1,解得i1>r1,所以折射光线向右偏折;根据折射定律有n=,由几何知识可知r1=r2,解得i1=i2,所以出
射光线与入射光线平行。故选C。]
1
题号
2
3
4
5
6
7
8
9
10
11
4.(2024·贵州卷)一种测量液体折射率的V形容器由两块材质相同的直角棱镜粘合,并封闭其前后两端制作而成。容器中盛有某种液体,一激光束从左边棱镜水平射入,通过液体后从右边棱镜射出,其光路如图所示。设棱镜和液体的折射率分别为n0、n,光在棱镜和液体中的传播速度分别为v0、v,
则( )
A.n
B.n
D.n>n0,v
题号
2
3
4
5
6
7
8
9
10
11
√
A [由题图可知光从棱镜进入液体中时,入射角小于折射角,根据折射定律可知n
1
题号
2
3
4
5
6
7
8
9
10
11
题组二 全反射现象的理解和应用
5.光的反射、折射及全反射是自然界中很常见的现象,在一次实验课上,某小组进行了实验:将一束单色细光束由空气(视为真空)沿着半径方向射入一块半圆柱形透明体,如图甲所示,对其从圆心O点射出后的折射光线的强度用相应传感器进行了记录,发现从O点射出的折射光线的强度随着夹角θ的变化而变化,变化情况如图乙的图线所示,则下列说法正确的是( )
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
A.当夹角θ小于30°时,在O点处既有反射光,又有折射光
B.圆柱形透明体对该单色光的全反射临界角为30°
C.圆柱形透明体对该单色光的折射率为2
D.圆柱形透明体对该单色光的折射率为
√
D [从题图乙中可以看出,当夹角θ小于30°时,没有折射光,A错误;当θ=30°,即入射角为60°时,折射光线的强度为零,故此时发生全反射,临界角为60°,B错误;因为全反射临界角为60°,所以n==,C错误,D正确。]
1
题号
2
3
4
5
6
7
8
9
10
11
6.由于大气层的存在,太阳光线在大气中折射,使得太阳“落山”后我们仍然能看见它。某同学为研究这一现象,建立了简化模型。将折射率很小的不均匀大气等效成折射率为的均匀大气,并将大气层的厚度等效为地球半径R。根据此模型,一个住在赤道上的人一天中能看到太阳的时长为( )
A.12小时
B.13小时
C.14小时
D.15小时
1
题号
2
3
4
5
6
7
8
9
10
11
√
C [太阳光是平行光,临界光路图如图所示,由几何关系可得临界光线的折射角满足sin r==,可知临界光线的折射角为30°,根据折射定律可得n==,解得i=45°,由几何关系可知,地球多转α角度便看不见太阳了,有α=60°-45°=15°,一个住在赤道上的人在太阳“落山”后还能看到太阳的时间为t=×24 h=1 h,同理可知,在太阳升起时也能提早一小时看到太阳,则一个住在赤道上的人一天中能看到太阳的时长为14 h。
故选C。]
1
题号
2
3
4
5
6
7
8
9
10
11
题组三 折射定律和全反射现象的综合应用
7.(2024·江苏宿迁一模)右图是某种新型光导纤维材料的一小段,材料呈圆柱状,其中MQ为直径,一束单色光以入射角α从空气射向圆心O,下列说法正确的是( )
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
A.光纤通信应用了光的衍射
B.单色光从MQ射入光导纤维时,折射角大于入射角
C.若α=45°时,单色光刚好不从MN射出,则光导纤维的折射率为
D.若光导纤维的折射率为2,则无论入射角α多大,单色光都不会从MN或QP射出
√
D [光纤通信应用了光的全反射,故A错误;单色光从MQ射入光导纤维时,即从光疏介质进入光密介质,折射角小于入射角,故B错误;若α=45°时,单色光刚好不从MN射出,光路图如图甲所示。
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
根据折射定律有n=,临界角满足sin C=,根据几何关系有C+r=90°,则光导纤维的折射率为n=,故C错误;无论入射角α为多少,单色光都不会从MN或QP射出,光导纤维的折射率最小时,光路图如图乙所示。
1
题号
2
3
4
5
6
7
8
9
10
11
根据折射定律有n′=,临界角为sin C′=,根据几何关系有C′+r′=90°,则光导纤维的折射率最小值为n′=<2,故若光导纤维的折射率为2,则无论入射角α为多少,单色光都不会从MN或QP射出,故D正确。故选D。]
8.冰雕展上,厚厚的冰墙内安装有LED光源S,冰墙表面平整而光滑,光源可视为点光源。小明想测量光源到墙面的距离h及冰的折射率n,设计了如下实验:如图(a)所示,将半径为R的圆形纸片贴在墙面上,圆心正对光源。用白纸板做屏,平行墙面从纸片处向后移动,当屏上黑影的半径等于2R时,测出屏到墙面的距离d,换用不同半径的纸片重复上述实验,得到多组数据,在坐标纸上画出d2-R2图像如图(b)所示,直线横截距为a,纵截距为b,则下列说法正确的是( )
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
A.光源到墙面的距离为
B.光源到墙面的距离为
C.冰的折射率为
D.冰的折射率为
√
A [如图所示,设到达圆形纸片边缘的光的入射角为r,折射角i,则由几何关系及折射定律可得n=,sin i=,sin r=,联立可得d2=R2+,结合题图(b)可得-1=-=b,所以h=,n=,故选A。]
1
题号
2
3
4
5
6
7
8
9
10
11
9.(2024·全国甲卷)一玻璃柱的折射率n=,其横截面为四分之一圆,圆的半径为R,如图所示。截面所在平面内,一束与AB边平行的光线从圆弧入射。入射光线与AB边的距离由小变大,距离为h时,光线进入柱体后射到BC边恰好发生全反射。求此时h与R的比值。
1
题号
2
3
4
5
6
7
8
9
10
11
[解析] 根据题意可画出入射光线与AB边的距离为h时的光路图,如图所示
由折射定律有n==
由全反射临界角公式有sin C0=
由几何关系有i=r+C0
h=R sin i
联立解得=。
1
题号
2
3
4
5
6
7
8
9
10
11
[答案]
10.(2024·江苏南京师大附中模拟)反光膜是一种广泛用于道路交通标志的材料,基本结构如图所示。光照射到反光膜的玻璃珠上时,经折射后射到反射层反射,最终平行于原入射方向反向射出玻璃珠。玻璃珠是半径为R的均匀球体,AB是入射光线,其出射光线与光线AB的间距为R。
1
题号
2
3
4
5
6
7
8
9
10
11
(1)请作出光线AB从射入到射出玻璃珠的完整光路图;
(2)求玻璃珠的折射率n。
1
题号
2
3
4
5
6
7
8
9
10
11
[解析] (1)光路图如图所示。
(2)设射入B点光线的入射角为θ1,折射角为θ2,则sin θ1==,则θ1=60°
由几何知识知θ1=2θ2,则θ2=30°
由折射定律有n=
解得n=。
1
题号
2
3
4
5
6
7
8
9
10
11
[答案] (1)见解析图 (2)
11.如图所示,透明玻璃体的上半部分是半球体,下半部分是圆柱体,半球体的半径为R,O为半球体的球心。圆柱体的底面半径和高也为R,现有一半径为R的圆环形平行光垂直于圆柱体底面射向半球体,OO1为圆光环的中心轴线,所有光线经折射后恰好经过圆柱体下表面圆心O1点,光线从O1射出后在玻璃体下方的水平光屏上形成圆形亮环,光到圆柱体底面的距离为R,光在真空中的传播速度为c。求:
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
(1)透明玻璃体的折射率;
(2)光从入射点传播到光屏所用的时间。
[解析] (1)作出光路图如图所示,设光线的入射角为α,折射角为β,则
由几何关系可得
R sin α=R
解得α=60°
由图可知α=2β
所以β=30°
由折射定律可知n==。
1
题号
2
3
4
5
6
7
8
9
10
11
1
题号
2
3
4
5
6
7
8
9
10
11
(2)光在透明玻璃体中的传播速度为v=
光在透明玻璃体中的传播时间为t1==
由图及折射定律知光线从O1点射出后与竖直方向的夹角为α=60°
所以光从透明玻璃体射出后到光屏所用的时间为t2==
则光从入射点传播到光屏所用的时间为t=t1+t2=。
[答案] (1) (2)
谢 谢 !
同课章节目录
