4.2指数函数(预习衔接.夯实基础.含解析)2025-2026学年高一上学期数学必修第一册人教A版(2019)
文档属性
| 名称 | 4.2指数函数(预习衔接.夯实基础.含解析)2025-2026学年高一上学期数学必修第一册人教A版(2019) |

|
|
| 格式 | docx | ||
| 文件大小 | 126.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 17:52:39 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
预习衔接.夯实基础 指数函数
一.选择题(共4小题)
1.(2024秋 西湖区校级期中)设,,c=3﹣2.3,则a,b,c的大小关系为( )
A.c<a<b B.a<b<c C.b<a<c D.a<c<b
2.(2024秋 浑南区校级期中)下列各式错误的是( )
A.30.8>30.7 B.0.75﹣0.1<0.750.1
C. D.0.50.4>0.50.6
3.(2024秋 朝阳区校级期中)已知,,则( )
A.a<c<b B.a<b<c C.b<c<a D.b<a<c
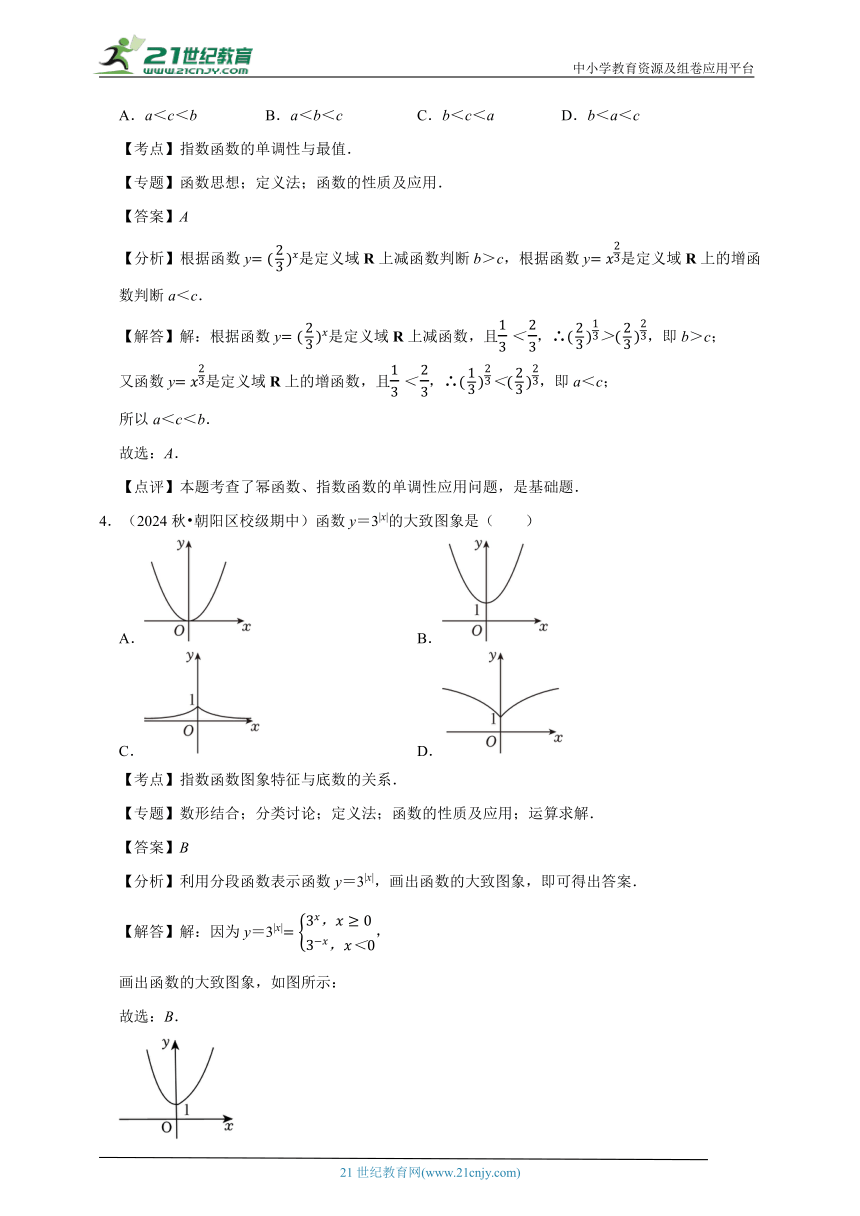
4.(2024秋 朝阳区校级期中)函数y=3|x|的大致图象是( )
A.B.C.D.
二.多选题(共3小题)
(多选)5.(2023秋 越秀区期末)下列结论正确的有( )
A.函数f(x)=loga(x+1)+loga(x﹣1)(a>0且a≠1)是偶函数
B.函数f(x)=2ax﹣2﹣1(a>0且a≠1)的图像恒过定点(2,1)
C.函数在R上单调递增
D.函数与函数y=﹣log2x的图像关于直线y=x对称
(多选)6.(2023秋 七里河区校级期末)若logab<0,则函数f(x)=ax+b的大致图象是( )
A. B.
C. D.
(多选)7.(2023秋 孝南区校级期末)若函数y=ax﹣2b﹣1(a>0且a≠0)的图象过第一、三、四象限,则( )
A.0<a<1 B.a>1 C.b>0 D.b<0
三.填空题(共4小题)
8.(2024秋 浦东新区校级期中)不等式与不等式x2+ax+b<0解集相同,则a+b= .
9.(2023秋 赤峰期末)函数的定义域为 .
10.(2023秋 浦东新区校级期末)若a>0,a≠1,则函数y=ax﹣1+2的图象一定过点 .
11.(2024春 宝山区期末)已知指数函数y=(m﹣2)x在R上是严格增函数,则实数m的取值范围是 .
四.解答题(共4小题)
12.(2023秋 静宁县校级期末)已知函数.
(1)若f(x)≥1,求实数x的取值范围;
(2)求f(x)的值域.
13.(2024春 昌邑区校级期末)已知函数f(x)=4x+a 2x.
(1)若a=﹣5,求不等式f(x)≤﹣4的解集;
(2)若x∈[﹣2,2]时,f(x)的最小值为﹣1,求a的值.
14.(2023秋 广昌县校级期末)已知指数函数y=(a2﹣3a+3)ax(a>0,a≠1)的反函数为y=f(x).
(1)求函数y=f(x)的解析式;
(2)已知函数g(x)=f(x2+1),求不等式g(2x+1)<g(3﹣x)的解集.
15.(2024春 辽宁期末)在生活中,喷漆房和烤漆房是重要的工业设备,它们在我们的生活中起着至关重要的作用.喷漆房的过滤系统主要作用是净化空气.能把喷漆过程中的有害物质过滤掉,过滤过程中有害物质含量y(单位:mg/L)与时间x(x≥0)(单位:h)间的关系为,其中y0,k为正常数,已知过滤2h消除了20%的有害物质.
(1)过滤4h后还剩百分之几的有害物质?
(2)要使有害物质减少80%,大约需要过滤多少时间(精确到1h)?参考数据:lg2≈0.3
预习衔接.夯实基础 指数函数
参考答案与试题解析
一.选择题(共4小题)
1.(2024秋 西湖区校级期中)设,,c=3﹣2.3,则a,b,c的大小关系为( )
A.c<a<b B.a<b<c C.b<a<c D.a<c<b
【考点】指数函数的单调性与最值;对数函数的单调性与最值.
【专题】函数思想;综合法;函数的性质及应用;运算求解.
【答案】C
【分析】利用指数函数与对数函数的性质分析判断即可.
【解答】解:∵y=3x为R上的增函数,﹣2.5<﹣2.3,
∴0<a3﹣2.5<c=3﹣2.3<1,
又b0,
∴b<a<c.
故选:C.
【点评】本题考查指数函数与对数函数的性质,属于基础题.
2.(2024秋 浑南区校级期中)下列各式错误的是( )
A.30.8>30.7 B.0.75﹣0.1<0.750.1
C. D.0.50.4>0.50.6
【考点】指数函数图象特征与底数的关系.
【专题】分类讨论;定义法;函数的性质及应用;运算求解.
【答案】B
【分析】根据指数函数的单调性逐项判断即可.
【解答】解:由对数函数y=ax的性质知,
当0<a<1时,y=ax在R上单调递减,所以0.75﹣0.1>0.750.1,0.50.4>0.50.6,选项B错误,选项D正确;
当a>1时,y=ax在R上单调递增,所以30.8>30.7,,选项A、C正确.
故选:B.
【点评】本题考查了指数函数的图象与性质应用问题,是基础题.
3.(2024秋 朝阳区校级期中)已知,,则( )
A.a<c<b B.a<b<c C.b<c<a D.b<a<c
【考点】指数函数的单调性与最值.
【专题】函数思想;定义法;函数的性质及应用.
【答案】A
【分析】根据函数y是定义域R上减函数判断b>c,根据函数y是定义域R上的增函数判断a<c.
【解答】解:根据函数y是定义域R上减函数,且,∴,即b>c;
又函数y是定义域R上的增函数,且,∴,即a<c;
所以a<c<b.
故选:A.
【点评】本题考查了幂函数、指数函数的单调性应用问题,是基础题.
4.(2024秋 朝阳区校级期中)函数y=3|x|的大致图象是( )
A. B.
C. D.
【考点】指数函数图象特征与底数的关系.
【专题】数形结合;分类讨论;定义法;函数的性质及应用;运算求解.
【答案】B
【分析】利用分段函数表示函数y=3|x|,画出函数的大致图象,即可得出答案.
【解答】解:因为y=3|x|,
画出函数的大致图象,如图所示:
故选:B.
【点评】本题考查了指数函数的图象与性质应用问题,是基础题.
二.多选题(共3小题)
(多选)5.(2023秋 越秀区期末)下列结论正确的有( )
A.函数f(x)=loga(x+1)+loga(x﹣1)(a>0且a≠1)是偶函数
B.函数f(x)=2ax﹣2﹣1(a>0且a≠1)的图像恒过定点(2,1)
C.函数在R上单调递增
D.函数与函数y=﹣log2x的图像关于直线y=x对称
【考点】指数函数图象特征与底数的关系;定义法求解函数的单调性.
【专题】函数思想;综合法;函数的性质及应用;运算求解.
【答案】BCD
【分析】根据题意,结合指数函数、对数函数,以及函数的单调性和反函数的关系,逐项判定,即可求解.
【解答】解:对于A中,函数f(x)=loga(x+1)+loga(x﹣1),则满足,
解得x>1,
即f(x)的定义域为(1,+∞),不关于原点对称,
所以f(x)为非奇非偶函数,故A不正确;
对于B中,函数f(x)=2ax﹣2﹣1(a>0且a≠1),
令x﹣2=0,可得x=2,
则f(2)=2a0﹣1=1,
所以f(x)恒过定点(2,1),所以B正确;
对于C中,函数,
因为函数y=ex+1为单调递增函数,且y>0
所以为递减函数,则为递增函数,所以C正确;
对于D中,由函数与函数互为反函数,
所以函数与函数y=﹣log2x的图像关于直线y=x对称,所以D正确.
故选:BCD.
【点评】本题主要考查了函数的单调性和奇偶性,考查了反函数的定义,属于基础题.
(多选)6.(2023秋 七里河区校级期末)若logab<0,则函数f(x)=ax+b的大致图象是( )
A. B.
C. D.
【考点】指数函数的图象;对数函数的图象;函数的图象与图象的变换.
【专题】分类讨论;数形结合法;函数的性质及应用;逻辑思维;直观想象.
【答案】BC
【分析】讨论0<a<1和a>1两种情况,结合对数函数单调性求解logab<0,再根据指数函数单调性分析判断即可.
【解答】解:由logab<0=loga1,可得:
当0<a<1时,因为y=logax在定义域内单调递减,所以b>1.
此时f(x)=ax+b>1,且f(x)在定义域内单调递减,选项B成立,D错误;
当a>1时,因为y=logax在定义域内单调递增,所以0<b<1,
此时f(x)=ax+b>b,不能保证f(x)>1,且f(x)在定义域内单调递增,选项A错误,C成立.
故选:BC.
【点评】本题考查了指数函数与对数函数的应用问题,是基础题.
(多选)7.(2023秋 孝南区校级期末)若函数y=ax﹣2b﹣1(a>0且a≠0)的图象过第一、三、四象限,则( )
A.0<a<1 B.a>1 C.b>0 D.b<0
【考点】指数函数的图象.
【专题】整体思想;综合法;函数的性质及应用;数学抽象.
【答案】BC
【分析】由已知结合指数函数的性质即可求解.
【解答】解:若函数y=ax﹣2b﹣1(a>0且a≠0)的图象过第一、三、四象限,
则,解得a>1,b>0.
故选:BC.
【点评】本题主要考查了指数函数的性质的应用,属于基础题.
三.填空题(共4小题)
8.(2024秋 浦东新区校级期中)不等式与不等式x2+ax+b<0解集相同,则a+b= ﹣5 .
【考点】指数函数的单调性与最值.
【专题】转化思想;定义法;不等式的解法及应用;运算求解.
【答案】﹣5.
【分析】根据y=2x在R上单调递增,判断大小列不等式进行解答即可.
【解答】解:不等式可化为23﹣3x,
因为y=2x在R上单调递增,
所以x2﹣2x﹣3<3﹣3x,整理得x2+x﹣6<0,
由题意知两不等式的解集相同,则a=1,b=﹣6,
所以a+b=﹣5.
故答案为:﹣5.
【点评】本题考查了函数与不等式的应用问题,是基础题.
9.(2023秋 赤峰期末)函数的定义域为 (﹣∞,1) .
【考点】指数函数的定义域.
【专题】函数思想;分析法;函数的性质及应用;运算求解.
【答案】(﹣∞,1).
【分析】由根式内部的代数式大于等于0及分式的分母不等于0求解即可得答案.
【解答】解:要使函数有意义,则1﹣x>0,
解得x<1.
∴函数的定义域为:(﹣∞,1).
故答案为:(﹣∞,1).
【点评】本题考查了函数的定义域及其求法,是基础题.
10.(2023秋 浦东新区校级期末)若a>0,a≠1,则函数y=ax﹣1+2的图象一定过点 (1,3) .
【考点】指数函数的图象.
【专题】函数的性质及应用.
【答案】见试题解答内容
【分析】利用指数函数过定点的性质进行判断.
【解答】解:方法1:平移法
∵y=ax过定点(0,1),
∴将函数y=ax向右平移1个单位,再向上平移2个单位得到y=ax﹣1+2,此时函数过定点(1,3),
方法2:解方程法
由x﹣1=0,解得x=1,
此时y=1+2=3,
即函数y=ax﹣1+2的图象一定过点(1,3).
故答案为:(1,3)
【点评】本题主要考查指数函数过定点的性质,如果x的系数为1,则可以使用平移法,但x的系数不为1,则用解方程的方法比较简单.
11.(2024春 宝山区期末)已知指数函数y=(m﹣2)x在R上是严格增函数,则实数m的取值范围是 {m|m>3} .
【考点】指数函数的图象.
【专题】转化思想;转化法;函数的性质及应用;运算求解.
【答案】{m|m>3}.
【分析】结合指数函数的性质,即可求解.
【解答】解:指数函数y=(m﹣2)x在R上是严格增函数,
则m﹣2>1,解得m>3,
故实数m的取值范围是{m|m>3}.
故答案为:{m|m>3}.
【点评】本题主要考查指数函数的性质,属于基础题.
四.解答题(共4小题)
12.(2023秋 静宁县校级期末)已知函数.
(1)若f(x)≥1,求实数x的取值范围;
(2)求f(x)的值域.
【考点】指数函数的值域.
【专题】函数思想;转化法;函数的性质及应用;运算求解.
【答案】(1)[0,2];
(2)(0,3].
【分析】(1)根据指数函数单调性可得﹣x2+2x≥0,结合二次不等式运算求解即可;
(2)根据二次函数分析可知﹣x2+2x≤1,结合指数函数性质求值域.
【解答】解:(1)因为,且y=3x在定义域R内单调递增,
则﹣x2+2x≥0,解得0≤x≤2,
所以实数x的取值范围是[0,2].
(2)因为﹣x2+2x=﹣(x﹣1)2+1≤1,当且仅当x=1时等号成立,
且y=3x在定义域R内单调递增,则,
又因为,所以f(x)的值域为(0,3].
【点评】本题考查了指数函数的图象与性质应用问题,是基础题.
13.(2024春 昌邑区校级期末)已知函数f(x)=4x+a 2x.
(1)若a=﹣5,求不等式f(x)≤﹣4的解集;
(2)若x∈[﹣2,2]时,f(x)的最小值为﹣1,求a的值.
【考点】指数函数及指数型复合函数的图象.
【专题】转化思想;综合法;函数的性质及应用;运算求解.
【答案】(1)[0,2];
(2)﹣2.
【分析】(1)当a=﹣5时,将不等式转化为(2x﹣1)(2x﹣4)≤0,并用指数函数的单调性求解;
(2)先使用换元法,将函数f(x)转化为,并分3类讨论函数g(t)的最小值即可.
【解答】解:(1)当a=﹣5时,不等式f(x)≤﹣4即为4x﹣5 2x+4≤0,
所以(2x﹣1)(2x﹣4)≤0,
则有1≤2x≤4,则0≤x≤2,
故不等式f(x)≤﹣4的解集为[0,2];
(2)令t=2x,x∈[﹣2,2],则,
f(x)=g(t)=t2+at开口向上,对称轴方程为,
①当,即时,,则,不符合题意;
②当,即时,,则a=﹣2;
③当,即a<﹣8时,g(t)min=g(4)=16+4a=﹣1,则,不满足条件.
综上所述,a的值为﹣2.
【点评】本题主要考查函数性质的综合应用,考查计算能力,属于中档题.
14.(2023秋 广昌县校级期末)已知指数函数y=(a2﹣3a+3)ax(a>0,a≠1)的反函数为y=f(x).
(1)求函数y=f(x)的解析式;
(2)已知函数g(x)=f(x2+1),求不等式g(2x+1)<g(3﹣x)的解集.
【考点】指数函数的单调性与最值;反函数;指数函数的图象.
【专题】转化思想;定义法;函数的性质及应用;运算求解.
【答案】(1)f(x)=log2x,x∈(0,+∞);
(2)(﹣4,).
【分析】(1)根据指数函数的定义列方程求出a的值,即可写出该函数的反函数;
(2)根据函数g(x)的奇偶性与单调性,把不等式g(2x+1)<g(3﹣x)化为|2x+1|<|3﹣x|,两边平分求解即可.
【解答】解:(1)指数函数y=(a2﹣3a+3)ax(a>0,a≠1)中,
a2﹣3a+3=1,解得a=1或a=2,所以a=2,函数y=2x;
反函数为y=f(x)=log2x,x∈(0,+∞);
(2)函数g(x)=f(x2+1)=log2(x2+1),
是定义域R上的偶函数,且在[0,+∞)上单调递增;
所以不等式g(2x+1)<g(3﹣x)可化为|2x+1|<|3﹣x|,
即(2x+1)2<(3﹣x)2,即3x2+10x﹣8<0,
解得﹣4<x,所以不等式的解集为(﹣4,).
【点评】本题考查了指数函数与对数函数的定义与性质应用问题,是基础题.
15.(2024春 辽宁期末)在生活中,喷漆房和烤漆房是重要的工业设备,它们在我们的生活中起着至关重要的作用.喷漆房的过滤系统主要作用是净化空气.能把喷漆过程中的有害物质过滤掉,过滤过程中有害物质含量y(单位:mg/L)与时间x(x≥0)(单位:h)间的关系为,其中y0,k为正常数,已知过滤2h消除了20%的有害物质.
(1)过滤4h后还剩百分之几的有害物质?
(2)要使有害物质减少80%,大约需要过滤多少时间(精确到1h)?参考数据:lg2≈0.3
【考点】指数函数的实际应用;对数的运算性质;根据实际问题选择函数类型.
【专题】函数思想;综合法;函数的性质及应用;运算求解.
【答案】(1)还剩64%的有害物质;
(2)大约需要过滤14小时.
【分析】(1)首先确定y0为初始含量,再代入条件,利用指数运算,即可求解;
(2)根据(1)的结果,代入条件,转化为求解指数方程.
【解答】解:(1)当x=0时,y=y0,
所以y0是初始有害物质的含量,
由题意可知,,得e﹣2k=0.8,
4h后有害物质含量,
所以过滤4小时后还剩64%的有害物质;
(2)设过滤t小时后,有害物质减少80%,即还剩20%,
则,
则,
则,
则t=14,
所以要使有害物质减少80%,大约需要过滤14小时.
【点评】本题考查了根据实际问题选择函数类型,考查了指数和对数的运算,考查了函数思想,属于中档题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.夯实基础 指数函数
一.选择题(共4小题)
1.(2024秋 西湖区校级期中)设,,c=3﹣2.3,则a,b,c的大小关系为( )
A.c<a<b B.a<b<c C.b<a<c D.a<c<b
2.(2024秋 浑南区校级期中)下列各式错误的是( )
A.30.8>30.7 B.0.75﹣0.1<0.750.1
C. D.0.50.4>0.50.6
3.(2024秋 朝阳区校级期中)已知,,则( )
A.a<c<b B.a<b<c C.b<c<a D.b<a<c
4.(2024秋 朝阳区校级期中)函数y=3|x|的大致图象是( )
A.B.C.D.
二.多选题(共3小题)
(多选)5.(2023秋 越秀区期末)下列结论正确的有( )
A.函数f(x)=loga(x+1)+loga(x﹣1)(a>0且a≠1)是偶函数
B.函数f(x)=2ax﹣2﹣1(a>0且a≠1)的图像恒过定点(2,1)
C.函数在R上单调递增
D.函数与函数y=﹣log2x的图像关于直线y=x对称
(多选)6.(2023秋 七里河区校级期末)若logab<0,则函数f(x)=ax+b的大致图象是( )
A. B.
C. D.
(多选)7.(2023秋 孝南区校级期末)若函数y=ax﹣2b﹣1(a>0且a≠0)的图象过第一、三、四象限,则( )
A.0<a<1 B.a>1 C.b>0 D.b<0
三.填空题(共4小题)
8.(2024秋 浦东新区校级期中)不等式与不等式x2+ax+b<0解集相同,则a+b= .
9.(2023秋 赤峰期末)函数的定义域为 .
10.(2023秋 浦东新区校级期末)若a>0,a≠1,则函数y=ax﹣1+2的图象一定过点 .
11.(2024春 宝山区期末)已知指数函数y=(m﹣2)x在R上是严格增函数,则实数m的取值范围是 .
四.解答题(共4小题)
12.(2023秋 静宁县校级期末)已知函数.
(1)若f(x)≥1,求实数x的取值范围;
(2)求f(x)的值域.
13.(2024春 昌邑区校级期末)已知函数f(x)=4x+a 2x.
(1)若a=﹣5,求不等式f(x)≤﹣4的解集;
(2)若x∈[﹣2,2]时,f(x)的最小值为﹣1,求a的值.
14.(2023秋 广昌县校级期末)已知指数函数y=(a2﹣3a+3)ax(a>0,a≠1)的反函数为y=f(x).
(1)求函数y=f(x)的解析式;
(2)已知函数g(x)=f(x2+1),求不等式g(2x+1)<g(3﹣x)的解集.
15.(2024春 辽宁期末)在生活中,喷漆房和烤漆房是重要的工业设备,它们在我们的生活中起着至关重要的作用.喷漆房的过滤系统主要作用是净化空气.能把喷漆过程中的有害物质过滤掉,过滤过程中有害物质含量y(单位:mg/L)与时间x(x≥0)(单位:h)间的关系为,其中y0,k为正常数,已知过滤2h消除了20%的有害物质.
(1)过滤4h后还剩百分之几的有害物质?
(2)要使有害物质减少80%,大约需要过滤多少时间(精确到1h)?参考数据:lg2≈0.3
预习衔接.夯实基础 指数函数
参考答案与试题解析
一.选择题(共4小题)
1.(2024秋 西湖区校级期中)设,,c=3﹣2.3,则a,b,c的大小关系为( )
A.c<a<b B.a<b<c C.b<a<c D.a<c<b
【考点】指数函数的单调性与最值;对数函数的单调性与最值.
【专题】函数思想;综合法;函数的性质及应用;运算求解.
【答案】C
【分析】利用指数函数与对数函数的性质分析判断即可.
【解答】解:∵y=3x为R上的增函数,﹣2.5<﹣2.3,
∴0<a3﹣2.5<c=3﹣2.3<1,
又b0,
∴b<a<c.
故选:C.
【点评】本题考查指数函数与对数函数的性质,属于基础题.
2.(2024秋 浑南区校级期中)下列各式错误的是( )
A.30.8>30.7 B.0.75﹣0.1<0.750.1
C. D.0.50.4>0.50.6
【考点】指数函数图象特征与底数的关系.
【专题】分类讨论;定义法;函数的性质及应用;运算求解.
【答案】B
【分析】根据指数函数的单调性逐项判断即可.
【解答】解:由对数函数y=ax的性质知,
当0<a<1时,y=ax在R上单调递减,所以0.75﹣0.1>0.750.1,0.50.4>0.50.6,选项B错误,选项D正确;
当a>1时,y=ax在R上单调递增,所以30.8>30.7,,选项A、C正确.
故选:B.
【点评】本题考查了指数函数的图象与性质应用问题,是基础题.
3.(2024秋 朝阳区校级期中)已知,,则( )
A.a<c<b B.a<b<c C.b<c<a D.b<a<c
【考点】指数函数的单调性与最值.
【专题】函数思想;定义法;函数的性质及应用.
【答案】A
【分析】根据函数y是定义域R上减函数判断b>c,根据函数y是定义域R上的增函数判断a<c.
【解答】解:根据函数y是定义域R上减函数,且,∴,即b>c;
又函数y是定义域R上的增函数,且,∴,即a<c;
所以a<c<b.
故选:A.
【点评】本题考查了幂函数、指数函数的单调性应用问题,是基础题.
4.(2024秋 朝阳区校级期中)函数y=3|x|的大致图象是( )
A. B.
C. D.
【考点】指数函数图象特征与底数的关系.
【专题】数形结合;分类讨论;定义法;函数的性质及应用;运算求解.
【答案】B
【分析】利用分段函数表示函数y=3|x|,画出函数的大致图象,即可得出答案.
【解答】解:因为y=3|x|,
画出函数的大致图象,如图所示:
故选:B.
【点评】本题考查了指数函数的图象与性质应用问题,是基础题.
二.多选题(共3小题)
(多选)5.(2023秋 越秀区期末)下列结论正确的有( )
A.函数f(x)=loga(x+1)+loga(x﹣1)(a>0且a≠1)是偶函数
B.函数f(x)=2ax﹣2﹣1(a>0且a≠1)的图像恒过定点(2,1)
C.函数在R上单调递增
D.函数与函数y=﹣log2x的图像关于直线y=x对称
【考点】指数函数图象特征与底数的关系;定义法求解函数的单调性.
【专题】函数思想;综合法;函数的性质及应用;运算求解.
【答案】BCD
【分析】根据题意,结合指数函数、对数函数,以及函数的单调性和反函数的关系,逐项判定,即可求解.
【解答】解:对于A中,函数f(x)=loga(x+1)+loga(x﹣1),则满足,
解得x>1,
即f(x)的定义域为(1,+∞),不关于原点对称,
所以f(x)为非奇非偶函数,故A不正确;
对于B中,函数f(x)=2ax﹣2﹣1(a>0且a≠1),
令x﹣2=0,可得x=2,
则f(2)=2a0﹣1=1,
所以f(x)恒过定点(2,1),所以B正确;
对于C中,函数,
因为函数y=ex+1为单调递增函数,且y>0
所以为递减函数,则为递增函数,所以C正确;
对于D中,由函数与函数互为反函数,
所以函数与函数y=﹣log2x的图像关于直线y=x对称,所以D正确.
故选:BCD.
【点评】本题主要考查了函数的单调性和奇偶性,考查了反函数的定义,属于基础题.
(多选)6.(2023秋 七里河区校级期末)若logab<0,则函数f(x)=ax+b的大致图象是( )
A. B.
C. D.
【考点】指数函数的图象;对数函数的图象;函数的图象与图象的变换.
【专题】分类讨论;数形结合法;函数的性质及应用;逻辑思维;直观想象.
【答案】BC
【分析】讨论0<a<1和a>1两种情况,结合对数函数单调性求解logab<0,再根据指数函数单调性分析判断即可.
【解答】解:由logab<0=loga1,可得:
当0<a<1时,因为y=logax在定义域内单调递减,所以b>1.
此时f(x)=ax+b>1,且f(x)在定义域内单调递减,选项B成立,D错误;
当a>1时,因为y=logax在定义域内单调递增,所以0<b<1,
此时f(x)=ax+b>b,不能保证f(x)>1,且f(x)在定义域内单调递增,选项A错误,C成立.
故选:BC.
【点评】本题考查了指数函数与对数函数的应用问题,是基础题.
(多选)7.(2023秋 孝南区校级期末)若函数y=ax﹣2b﹣1(a>0且a≠0)的图象过第一、三、四象限,则( )
A.0<a<1 B.a>1 C.b>0 D.b<0
【考点】指数函数的图象.
【专题】整体思想;综合法;函数的性质及应用;数学抽象.
【答案】BC
【分析】由已知结合指数函数的性质即可求解.
【解答】解:若函数y=ax﹣2b﹣1(a>0且a≠0)的图象过第一、三、四象限,
则,解得a>1,b>0.
故选:BC.
【点评】本题主要考查了指数函数的性质的应用,属于基础题.
三.填空题(共4小题)
8.(2024秋 浦东新区校级期中)不等式与不等式x2+ax+b<0解集相同,则a+b= ﹣5 .
【考点】指数函数的单调性与最值.
【专题】转化思想;定义法;不等式的解法及应用;运算求解.
【答案】﹣5.
【分析】根据y=2x在R上单调递增,判断大小列不等式进行解答即可.
【解答】解:不等式可化为23﹣3x,
因为y=2x在R上单调递增,
所以x2﹣2x﹣3<3﹣3x,整理得x2+x﹣6<0,
由题意知两不等式的解集相同,则a=1,b=﹣6,
所以a+b=﹣5.
故答案为:﹣5.
【点评】本题考查了函数与不等式的应用问题,是基础题.
9.(2023秋 赤峰期末)函数的定义域为 (﹣∞,1) .
【考点】指数函数的定义域.
【专题】函数思想;分析法;函数的性质及应用;运算求解.
【答案】(﹣∞,1).
【分析】由根式内部的代数式大于等于0及分式的分母不等于0求解即可得答案.
【解答】解:要使函数有意义,则1﹣x>0,
解得x<1.
∴函数的定义域为:(﹣∞,1).
故答案为:(﹣∞,1).
【点评】本题考查了函数的定义域及其求法,是基础题.
10.(2023秋 浦东新区校级期末)若a>0,a≠1,则函数y=ax﹣1+2的图象一定过点 (1,3) .
【考点】指数函数的图象.
【专题】函数的性质及应用.
【答案】见试题解答内容
【分析】利用指数函数过定点的性质进行判断.
【解答】解:方法1:平移法
∵y=ax过定点(0,1),
∴将函数y=ax向右平移1个单位,再向上平移2个单位得到y=ax﹣1+2,此时函数过定点(1,3),
方法2:解方程法
由x﹣1=0,解得x=1,
此时y=1+2=3,
即函数y=ax﹣1+2的图象一定过点(1,3).
故答案为:(1,3)
【点评】本题主要考查指数函数过定点的性质,如果x的系数为1,则可以使用平移法,但x的系数不为1,则用解方程的方法比较简单.
11.(2024春 宝山区期末)已知指数函数y=(m﹣2)x在R上是严格增函数,则实数m的取值范围是 {m|m>3} .
【考点】指数函数的图象.
【专题】转化思想;转化法;函数的性质及应用;运算求解.
【答案】{m|m>3}.
【分析】结合指数函数的性质,即可求解.
【解答】解:指数函数y=(m﹣2)x在R上是严格增函数,
则m﹣2>1,解得m>3,
故实数m的取值范围是{m|m>3}.
故答案为:{m|m>3}.
【点评】本题主要考查指数函数的性质,属于基础题.
四.解答题(共4小题)
12.(2023秋 静宁县校级期末)已知函数.
(1)若f(x)≥1,求实数x的取值范围;
(2)求f(x)的值域.
【考点】指数函数的值域.
【专题】函数思想;转化法;函数的性质及应用;运算求解.
【答案】(1)[0,2];
(2)(0,3].
【分析】(1)根据指数函数单调性可得﹣x2+2x≥0,结合二次不等式运算求解即可;
(2)根据二次函数分析可知﹣x2+2x≤1,结合指数函数性质求值域.
【解答】解:(1)因为,且y=3x在定义域R内单调递增,
则﹣x2+2x≥0,解得0≤x≤2,
所以实数x的取值范围是[0,2].
(2)因为﹣x2+2x=﹣(x﹣1)2+1≤1,当且仅当x=1时等号成立,
且y=3x在定义域R内单调递增,则,
又因为,所以f(x)的值域为(0,3].
【点评】本题考查了指数函数的图象与性质应用问题,是基础题.
13.(2024春 昌邑区校级期末)已知函数f(x)=4x+a 2x.
(1)若a=﹣5,求不等式f(x)≤﹣4的解集;
(2)若x∈[﹣2,2]时,f(x)的最小值为﹣1,求a的值.
【考点】指数函数及指数型复合函数的图象.
【专题】转化思想;综合法;函数的性质及应用;运算求解.
【答案】(1)[0,2];
(2)﹣2.
【分析】(1)当a=﹣5时,将不等式转化为(2x﹣1)(2x﹣4)≤0,并用指数函数的单调性求解;
(2)先使用换元法,将函数f(x)转化为,并分3类讨论函数g(t)的最小值即可.
【解答】解:(1)当a=﹣5时,不等式f(x)≤﹣4即为4x﹣5 2x+4≤0,
所以(2x﹣1)(2x﹣4)≤0,
则有1≤2x≤4,则0≤x≤2,
故不等式f(x)≤﹣4的解集为[0,2];
(2)令t=2x,x∈[﹣2,2],则,
f(x)=g(t)=t2+at开口向上,对称轴方程为,
①当,即时,,则,不符合题意;
②当,即时,,则a=﹣2;
③当,即a<﹣8时,g(t)min=g(4)=16+4a=﹣1,则,不满足条件.
综上所述,a的值为﹣2.
【点评】本题主要考查函数性质的综合应用,考查计算能力,属于中档题.
14.(2023秋 广昌县校级期末)已知指数函数y=(a2﹣3a+3)ax(a>0,a≠1)的反函数为y=f(x).
(1)求函数y=f(x)的解析式;
(2)已知函数g(x)=f(x2+1),求不等式g(2x+1)<g(3﹣x)的解集.
【考点】指数函数的单调性与最值;反函数;指数函数的图象.
【专题】转化思想;定义法;函数的性质及应用;运算求解.
【答案】(1)f(x)=log2x,x∈(0,+∞);
(2)(﹣4,).
【分析】(1)根据指数函数的定义列方程求出a的值,即可写出该函数的反函数;
(2)根据函数g(x)的奇偶性与单调性,把不等式g(2x+1)<g(3﹣x)化为|2x+1|<|3﹣x|,两边平分求解即可.
【解答】解:(1)指数函数y=(a2﹣3a+3)ax(a>0,a≠1)中,
a2﹣3a+3=1,解得a=1或a=2,所以a=2,函数y=2x;
反函数为y=f(x)=log2x,x∈(0,+∞);
(2)函数g(x)=f(x2+1)=log2(x2+1),
是定义域R上的偶函数,且在[0,+∞)上单调递增;
所以不等式g(2x+1)<g(3﹣x)可化为|2x+1|<|3﹣x|,
即(2x+1)2<(3﹣x)2,即3x2+10x﹣8<0,
解得﹣4<x,所以不等式的解集为(﹣4,).
【点评】本题考查了指数函数与对数函数的定义与性质应用问题,是基础题.
15.(2024春 辽宁期末)在生活中,喷漆房和烤漆房是重要的工业设备,它们在我们的生活中起着至关重要的作用.喷漆房的过滤系统主要作用是净化空气.能把喷漆过程中的有害物质过滤掉,过滤过程中有害物质含量y(单位:mg/L)与时间x(x≥0)(单位:h)间的关系为,其中y0,k为正常数,已知过滤2h消除了20%的有害物质.
(1)过滤4h后还剩百分之几的有害物质?
(2)要使有害物质减少80%,大约需要过滤多少时间(精确到1h)?参考数据:lg2≈0.3
【考点】指数函数的实际应用;对数的运算性质;根据实际问题选择函数类型.
【专题】函数思想;综合法;函数的性质及应用;运算求解.
【答案】(1)还剩64%的有害物质;
(2)大约需要过滤14小时.
【分析】(1)首先确定y0为初始含量,再代入条件,利用指数运算,即可求解;
(2)根据(1)的结果,代入条件,转化为求解指数方程.
【解答】解:(1)当x=0时,y=y0,
所以y0是初始有害物质的含量,
由题意可知,,得e﹣2k=0.8,
4h后有害物质含量,
所以过滤4小时后还剩64%的有害物质;
(2)设过滤t小时后,有害物质减少80%,即还剩20%,
则,
则,
则,
则t=14,
所以要使有害物质减少80%,大约需要过滤14小时.
【点评】本题考查了根据实际问题选择函数类型,考查了指数和对数的运算,考查了函数思想,属于中档题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
