13.2.2三角形的中线、角平分线、高 课件(共39张PPT) 人教版(2024)数学八年级上册
文档属性
| 名称 | 13.2.2三角形的中线、角平分线、高 课件(共39张PPT) 人教版(2024)数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 44.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 16:19:14 | ||
图片预览





文档简介
(共39张PPT)
人教版 八年级上册
13.1
第十三章 三角形
三角形的中线、
角平分线、高
情境引入
QING JING YIN RU
如图,有一块三角形的菜地,现要求分成面积比为1:1:2三块,且图中A处是三块菜地的共同水源处,应该怎么分?
A
复习回顾
FU XI HUI GU
回顾:什么叫垂线?线段中点?角平分线?
垂线:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.
线段中点:把一条线段分成两条相等的线段的点.
角的平分线:一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
A
B
O
B
A
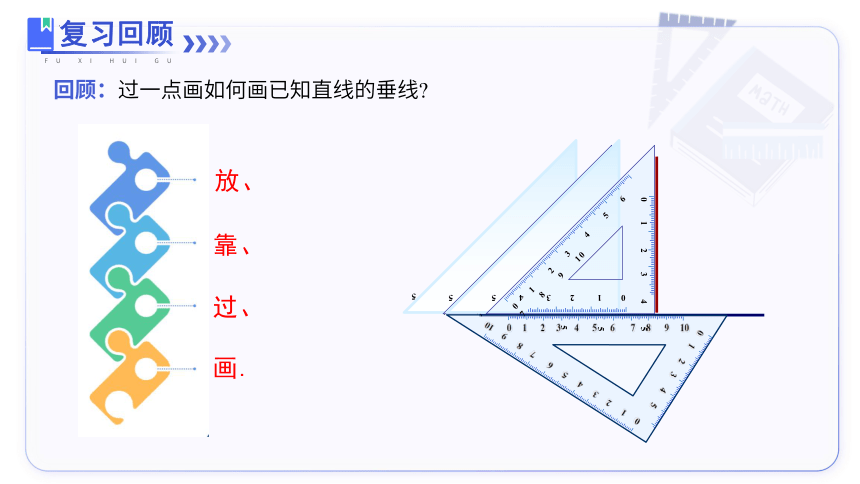
回顾:过一点画如何画已知直线的垂线
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
放、
靠、
过、
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
画.
复习回顾
FU XI HUI GU
新知探究
XIN ZHI TAN JIU
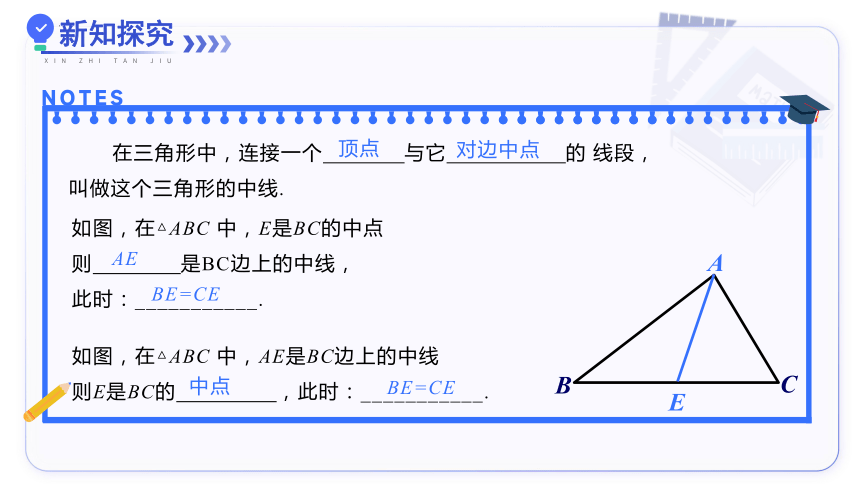
在三角形中,连接一个 与它 的 线段,
叫做这个三角形的中线.
顶点
对边中点
如图,在△ABC 中,E是BC的中点
则 是BC边上的中线,
此时:___________.
B
C
A
E
AE
BE=CE
如图,在△ABC 中,AE是BC边上的中线
则E是BC的 ,此时:___________.
中点
BE=CE
新知探究
XIN ZHI TAN JIU
思考
每一个三角形都有 个顶点,因此每一个三角形都有 条中线.
如图,画出三角形的中线.
3
3
这三条中线之间有怎样的位置关系
锐角三角形的三条中线是在三角形的内部还是外部
锐角三角形的三条中线交于同一点.
锐角三角形的三条中线都在三角形的内部.
思考
思考
新知探究
XIN ZHI TAN JIU
思考
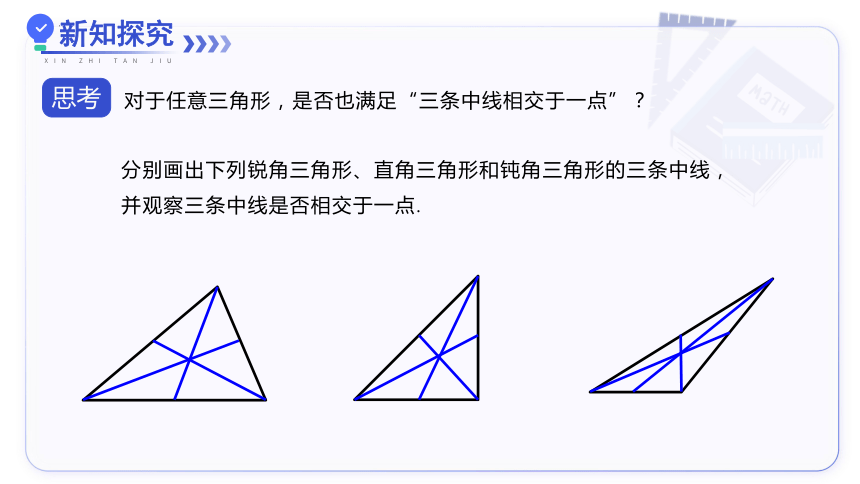
对于任意三角形,是否也满足“三条中线相交于一点”?
分别画出下列锐角三角形、直角三角形和钝角三角形的三条中线,
并观察三条中线是否相交于一点.
新知探究
XIN ZHI TAN JIU
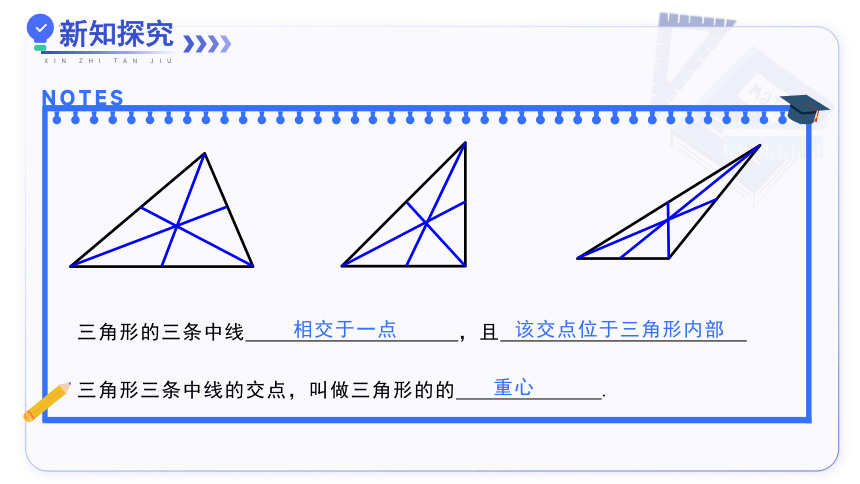
三角形的三条中线 ,且
相交于一点
该交点位于三角形内部
三角形三条中线的交点,叫做三角形的的 .
重心
新知探究
XIN ZHI TAN JIU
思考
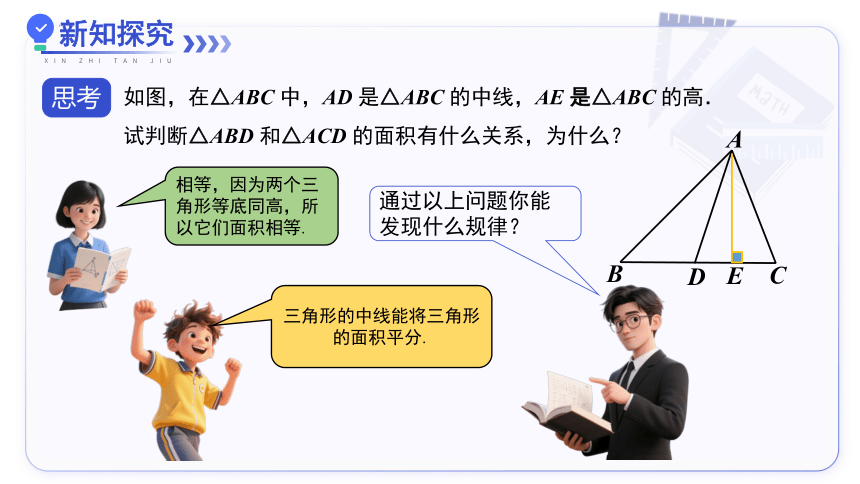
如图,在△ABC 中,AD 是△ABC 的中线,AE 是△ABC 的高.
试判断△ABD 和△ACD 的面积有什么关系,为什么?
B
C
D
E
A
通过以上问题你能发现什么规律?
三角形的中线能将三角形的面积平分.
相等,因为两个三角形等底同高,所以它们面积相等.
新知探究
XIN ZHI TAN JIU
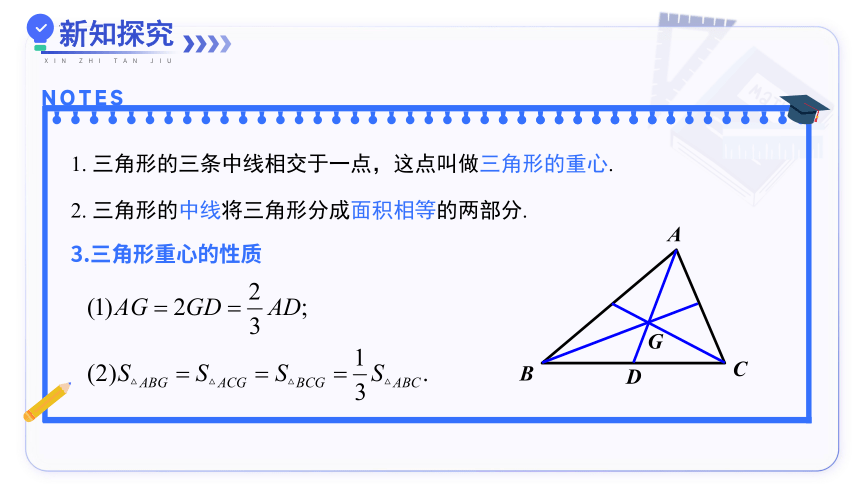
1. 三角形的三条中线相交于一点,这点叫做三角形的重心.
2. 三角形的中线将三角形分成面积相等的两部分.
3.三角形重心的性质
A
C
D
B
G
典例精析
DIAN LI JING XI
例1
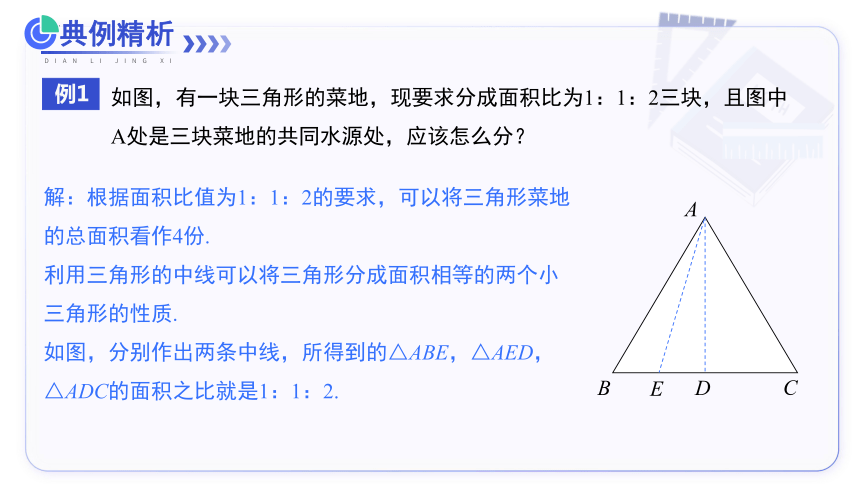
如图,有一块三角形的菜地,现要求分成面积比为1:1:2三块,且图中A处是三块菜地的共同水源处,应该怎么分?
解:根据面积比值为1:1:2的要求,可以将三角形菜地的总面积看作4份.
利用三角形的中线可以将三角形分成面积相等的两个小三角形的性质.
如图,分别作出两条中线,所得到的△ABE,△AED,△ADC的面积之比就是1:1:2.
A
B
C
E
D
典例精析
DIAN LI JING XI
例2
如图,AD为△ABC的中线,AB=12cm,△ABD和△ADC的周长差是4cm,
求△ABC的边AC 的长(AC<AB).
解:∵AD为△ABC的中线
∴BD=CD
∵△ABD和△ADC的周长差是4cm
∴AB+AD+BD﹣(AC+AD+CD)
=AB+AD+BD﹣AC﹣AD﹣BD
=AB﹣AC=4cm
∵AB=12cm
∴AC=AB﹣4cm=8cm
∴△ABC的边AC的长为8cm
你能把两个三角形的周长差用线段表示出来吗?
典例精析
DIAN LI JING XI
例3
如图,在△ABC 中,E 是 BC 上的一点,EC=2BE,点 D 是 AC 的中点,设△ABC,△ADF 和△BEF 的面积分别为 S△ABC,S△ADF 和 S△BEF,且 S△ABC =12,求 S△ADF-S△BEF 的值.
解:∵ 点 D 是 AC 的中点,∴ AD= AC.
∵ S△ABC=12,∴ S△ABD= S△ABC=×12=6.
∵ EC=2BE,S△ABC=12,
∴ S△ABE= S△ABC=×12=4.
∵ S△ABD-S△ABE =(S△ADF+S△ABF)-(S△ABF+S△BEF) =S△ADF-S△BEF,
∴ S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.
三角形的中线在面积中的常用结论
典例精析
DIAN LI JING XI
三角形的中线将三角形分成面积相等的两部分.
高相等时,面积的比等于底边的比;
底相等时,面积的比等于高的比.
新知探究
XIN ZHI TAN JIU
思考
你能类比三角形的中线的定义,说明什么是三角形的角平分线吗?
在三角形中,一个内角的 与它的 相交,这个角
的 与 之间的线段,叫做三角形的角平分线.
平分线
对边
顶点
交点
如图,在△ABC 中,∠1=∠2
则 是∠A的角平分线
1
2
A
B
C
D
AD
如图,在△ABC 中,AD是∠A的角平分线
则___________
∠1=∠2
新知探究
XIN ZHI TAN JIU
思考
A
B
C
D
相同点是: ∠ABD = ∠CBD;
不同点是:前者是线段,后者是射线.
三角形的角平分线与角的平分线相同吗
新知探究
XIN ZHI TAN JIU
思考
每一个三角形都有 个内角,因此每一个三角形都有 条角平分线.
如图,画出三角形的角平分线.
3
3
这三条角平分线之间有怎样的位置关系
锐角三角形的三条角平分线是在三角形的内部还是外部
锐角三角形的三条角平分线交于同一点.
锐角三角形的三条角平分线都在三角形的内部.
思考
新知探究
XIN ZHI TAN JIU
思考
对于任意三角形,是否也满足“三条角平分线相交于一点”?
分别画出下列锐角三角形、直角三角形和钝角三角形的三条角平分线,
并观察三条角平分线是否相交于一点.
新知探究
XIN ZHI TAN JIU
三角形的三条角平分线 ,且 ,
该点称为三角形的 .
相交于一点
该交点位于三角形内部
三角形的角平分线是一条 .
线段
内心
典例精析
DIAN LI JING XI
例4
如图,在△ABC中,AD⊥BC,AE平分∠BAC(∠B>∠C). 若∠B=80°,∠C=30°,求∠DAE.
解:∵在△ABC中, ∠B=80°,∠C=30°,
∴∠BAC=70°.
∵AE平分∠BAC,
∴∠BAC=2∠BAE=2∠CAE.
∵∠BAC=70°, ∴∠BAE=35°.
∵AD⊥BC,∠B=80°, ∴∠BAD=10°.
∴ ∠DAE=∠BAE-∠BAD=35°-10°=25°.
D
E
┐
B
A
C
典例精析
DIAN LI JING XI
例4
如图,在△ABC中,AD⊥BC,AE平分∠BAC(∠B>∠C). 若∠B=x°,
∠C=y°,求∠DAE(用x,y表示).
解:∵在△ABC中, ∠B=x°,∠C=y°,
∴∠BAC=(180-x-y)°.
∵AE平分∠BAC,
∴∠BAC=2∠BAE=2∠CAE.
∴∠BAE=90°-0.5(x+y)°.
∵AD⊥BC,∠B=80°, ∴∠BAD=(90-x)°.
∴ ∠DAE=∠BAE-∠BAD=0.5(x-y)°.
D
E
┐
B
A
C
从特殊到一般!
新知探究
XIN ZHI TAN JIU
从三角形的一个顶点向它的 所在的直线做垂线, 和
之间的 叫做三角形的高.
对边
顶点
垂足
线段
如图,在△ABC 中,AD⊥BC ,点D是垂足,
则 是△ABC的边BC上的高.
此时:_________________________.
A
B
C
D
AD
∠ADB = ∠ADC = 90°
注意:
标明垂直的记号和垂足的字母.
高的叙述方法(如图):有三种
新知探究
XIN ZHI TAN JIU
② AD⊥BC,垂足为 D.
③ 点 D 在 BC 上,且∠BDA =∠CDA = 90°.
① AD 是△ABC 的高.
A
B
C
D
新知探究
XIN ZHI TAN JIU
每一个三角形都有 个顶点,因此每一个三角形都有 条高.
如图,画出三角形的高.
3
3
这三条高之间有怎样的位置关系
锐角三角形的三条高是在三角形的内部还是外部
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
思考
思考
新知探究
XIN ZHI TAN JIU
思考
对于任意三角形,是否也满足“三条高相交于一点”
分别画出下列锐角三角形、直角三角形和钝角三角形的三条高,
并观察三条高是否相交于一点.
A
C
B
A
C
B
A
C
B
新知探究
XIN ZHI TAN JIU
(1)锐角三角形
O
A
B
C
D
E
F
①BC边上的高为
AC边上的高为
AB边上的高为
AD
BE
CF
②锐角三角形的三条高(线段AD、BE、CF) ,
且 .
相交于一点
该点位于三角形的内部
新知探究
XIN ZHI TAN JIU
(2)直角三角形
①AC边上的高为
直角边AB上的高为
直角边BC上的高为
BD
CB
AB
②直角三角形的三条高 .
相交于直角顶点
A
B
C
D
新知探究
XIN ZHI TAN JIU
(3)钝角三角形
A
B
C
D
E
F
①BC边上的高为
AB边上的高为
AC边上的高为
AD
CE
BF
②钝角三角形的三条高 .
不相交于一点
新知探究
XIN ZHI TAN JIU
思考
A
B
C
D
F
钝角三角形的三条高相交吗?
它们所在的直线交于一点吗?
这点位于何处?
O
E
钝角三角形的三条高不相交.
钝角三角形的三条高所在直线交于一点,
并且这个点在三角形外部.
思考
新知探究
XIN ZHI TAN JIU
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形
内部
直角顶点
三角形
外部
三角形三条高所在直线的交点称为三角形的 .
垂心
典例精析
DIAN LI JING XI
例5
下列各组图形中,哪一组图形中AD是△ABC的高( )
B
AD一定要垂直于三角形的另一条边.
典例精析
DIAN LI JING XI
例6
如图,在△ABC中,AC=8,BC=4,高BD=3,试作出BC边上的高AE,
并求AE的长.
解:如图,过点A作BC边上的高线AE,
交CB延长线于点E
∵BC AE= AC BD,AC=8,BC=4,高BD=3
∴ ×4AE= ×8×3
解得 AE=6
∴AE的长为6
E
课堂小结
QING JING YIN RU
三角形的中线
图形
几何语言
三角形中的重要线段
三角形的
角平分线
图形
几何语言
三角形的高线
图形
几何语言
∵AD是△ABC的高线.
∴AD⊥BC,∠ADB=∠ADC=90°
∵ AD是△ABC的BC上的中线
∴ BD=CD= BC
∵AD是△ABC的∠BAC的平分线
∴ ∠1=∠2= ∠BAC
当堂练习
QING JING YIN RU
1.如图,CM是△ABC的中线,AB=10cm,则BM的长为( )
A.7cm B.6cm
C.5cm D.4cm
C
2. 如图,在△ABC 中,∠ACB = 90°,CD⊥AB,图中线段
中可以作为△ABC 的高的有 ( )
A.2 条 B.3 条
C.4 条 D.5 条
B
当堂练习
QING JING YIN RU
3.填空:
(1) 如图①,AD,BE,CF 是△ABC 的三条中线,则
AB = 2__,BD = __,AE = __ .
(2) 如图②,AD,BE,CF 是△ABC 的三条角平分线,
则∠1 =_______, ∠3 =_______,∠ABC = 2_____.
图①
图②
AF
DC
∠CAD
∠2
∠BCF
A
B
C
D
E
F
AC
当堂练习
QING JING YIN RU
4.BD是△ABC的中线,AB=5,BC=3,求△ABD和△BCD的周长的差.
解:∵BD是△ABC的中线,
∴AD=CD,
∴△ABD和△BCD的周长的差
=(AB+BD+AD)-(BC+BD+CD)
=AB﹣BC,
∵AB=5,BC=3,
∴△ABD和△BCD的周长的差=5﹣3=2
当堂练习
QING JING YIN RU
解:∵ CD 是△ABC 的中线,
∴ BD = AD.
∵ BC - AC = 5cm,
∴△DBC 与△ADC 的周长差是 5 cm.
又∵△DBC 的周长为 25 cm,
∴△ADC 的周长为 25 - 5 = 20 (cm).
5. 如图,在△ABC 中,CD 是中线,已知 BC - AC = 5 cm, △DBC 的周长为 25 cm,求△ADC 的周长.
A
D
B
C
当堂练习
QING JING YIN RU
6.如图,在△ABC中,AB=AC,DB为△ABC的中线,且BD将△ABC周长分为12cm与15cm两部分,求三角形各边长.
解:∵DB为△ABC的中线
∴AD=CD
设AD=CD=x,则AB=2x
当x+2x=12,解得x=4
BC+x=15,解得BC=11
此时△ABC的三边长为:AB=AC=8,BC=11
当x+2x=15,BC+x=12,解得x=5,BC=7
此时△ABC的三边长为:AB=AC=10,BC=7
当堂练习
QING JING YIN RU
7. 如图所示,在△ABC 中,AB=AC=5,BC=6,AD⊥BC 于点 D,且 AD=4,若点 P 在边 AC 上移动,求 BP 的最小值.
解:根据垂线段最短,可知当 BP⊥AC 时,
BP 有最小值.
此时由△ABC 的面积公式可知,
AD · BC= BP · AC.
代入数值,可解得 BP= .
P
人教版 八年级上册
13.1
第十三章 三角形
三角形的中线、
角平分线、高
情境引入
QING JING YIN RU
如图,有一块三角形的菜地,现要求分成面积比为1:1:2三块,且图中A处是三块菜地的共同水源处,应该怎么分?
A
复习回顾
FU XI HUI GU
回顾:什么叫垂线?线段中点?角平分线?
垂线:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.
线段中点:把一条线段分成两条相等的线段的点.
角的平分线:一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
A
B
O
B
A
回顾:过一点画如何画已知直线的垂线
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
放、
靠、
过、
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
画.
复习回顾
FU XI HUI GU
新知探究
XIN ZHI TAN JIU
在三角形中,连接一个 与它 的 线段,
叫做这个三角形的中线.
顶点
对边中点
如图,在△ABC 中,E是BC的中点
则 是BC边上的中线,
此时:___________.
B
C
A
E
AE
BE=CE
如图,在△ABC 中,AE是BC边上的中线
则E是BC的 ,此时:___________.
中点
BE=CE
新知探究
XIN ZHI TAN JIU
思考
每一个三角形都有 个顶点,因此每一个三角形都有 条中线.
如图,画出三角形的中线.
3
3
这三条中线之间有怎样的位置关系
锐角三角形的三条中线是在三角形的内部还是外部
锐角三角形的三条中线交于同一点.
锐角三角形的三条中线都在三角形的内部.
思考
思考
新知探究
XIN ZHI TAN JIU
思考
对于任意三角形,是否也满足“三条中线相交于一点”?
分别画出下列锐角三角形、直角三角形和钝角三角形的三条中线,
并观察三条中线是否相交于一点.
新知探究
XIN ZHI TAN JIU
三角形的三条中线 ,且
相交于一点
该交点位于三角形内部
三角形三条中线的交点,叫做三角形的的 .
重心
新知探究
XIN ZHI TAN JIU
思考
如图,在△ABC 中,AD 是△ABC 的中线,AE 是△ABC 的高.
试判断△ABD 和△ACD 的面积有什么关系,为什么?
B
C
D
E
A
通过以上问题你能发现什么规律?
三角形的中线能将三角形的面积平分.
相等,因为两个三角形等底同高,所以它们面积相等.
新知探究
XIN ZHI TAN JIU
1. 三角形的三条中线相交于一点,这点叫做三角形的重心.
2. 三角形的中线将三角形分成面积相等的两部分.
3.三角形重心的性质
A
C
D
B
G
典例精析
DIAN LI JING XI
例1
如图,有一块三角形的菜地,现要求分成面积比为1:1:2三块,且图中A处是三块菜地的共同水源处,应该怎么分?
解:根据面积比值为1:1:2的要求,可以将三角形菜地的总面积看作4份.
利用三角形的中线可以将三角形分成面积相等的两个小三角形的性质.
如图,分别作出两条中线,所得到的△ABE,△AED,△ADC的面积之比就是1:1:2.
A
B
C
E
D
典例精析
DIAN LI JING XI
例2
如图,AD为△ABC的中线,AB=12cm,△ABD和△ADC的周长差是4cm,
求△ABC的边AC 的长(AC<AB).
解:∵AD为△ABC的中线
∴BD=CD
∵△ABD和△ADC的周长差是4cm
∴AB+AD+BD﹣(AC+AD+CD)
=AB+AD+BD﹣AC﹣AD﹣BD
=AB﹣AC=4cm
∵AB=12cm
∴AC=AB﹣4cm=8cm
∴△ABC的边AC的长为8cm
你能把两个三角形的周长差用线段表示出来吗?
典例精析
DIAN LI JING XI
例3
如图,在△ABC 中,E 是 BC 上的一点,EC=2BE,点 D 是 AC 的中点,设△ABC,△ADF 和△BEF 的面积分别为 S△ABC,S△ADF 和 S△BEF,且 S△ABC =12,求 S△ADF-S△BEF 的值.
解:∵ 点 D 是 AC 的中点,∴ AD= AC.
∵ S△ABC=12,∴ S△ABD= S△ABC=×12=6.
∵ EC=2BE,S△ABC=12,
∴ S△ABE= S△ABC=×12=4.
∵ S△ABD-S△ABE =(S△ADF+S△ABF)-(S△ABF+S△BEF) =S△ADF-S△BEF,
∴ S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.
三角形的中线在面积中的常用结论
典例精析
DIAN LI JING XI
三角形的中线将三角形分成面积相等的两部分.
高相等时,面积的比等于底边的比;
底相等时,面积的比等于高的比.
新知探究
XIN ZHI TAN JIU
思考
你能类比三角形的中线的定义,说明什么是三角形的角平分线吗?
在三角形中,一个内角的 与它的 相交,这个角
的 与 之间的线段,叫做三角形的角平分线.
平分线
对边
顶点
交点
如图,在△ABC 中,∠1=∠2
则 是∠A的角平分线
1
2
A
B
C
D
AD
如图,在△ABC 中,AD是∠A的角平分线
则___________
∠1=∠2
新知探究
XIN ZHI TAN JIU
思考
A
B
C
D
相同点是: ∠ABD = ∠CBD;
不同点是:前者是线段,后者是射线.
三角形的角平分线与角的平分线相同吗
新知探究
XIN ZHI TAN JIU
思考
每一个三角形都有 个内角,因此每一个三角形都有 条角平分线.
如图,画出三角形的角平分线.
3
3
这三条角平分线之间有怎样的位置关系
锐角三角形的三条角平分线是在三角形的内部还是外部
锐角三角形的三条角平分线交于同一点.
锐角三角形的三条角平分线都在三角形的内部.
思考
新知探究
XIN ZHI TAN JIU
思考
对于任意三角形,是否也满足“三条角平分线相交于一点”?
分别画出下列锐角三角形、直角三角形和钝角三角形的三条角平分线,
并观察三条角平分线是否相交于一点.
新知探究
XIN ZHI TAN JIU
三角形的三条角平分线 ,且 ,
该点称为三角形的 .
相交于一点
该交点位于三角形内部
三角形的角平分线是一条 .
线段
内心
典例精析
DIAN LI JING XI
例4
如图,在△ABC中,AD⊥BC,AE平分∠BAC(∠B>∠C). 若∠B=80°,∠C=30°,求∠DAE.
解:∵在△ABC中, ∠B=80°,∠C=30°,
∴∠BAC=70°.
∵AE平分∠BAC,
∴∠BAC=2∠BAE=2∠CAE.
∵∠BAC=70°, ∴∠BAE=35°.
∵AD⊥BC,∠B=80°, ∴∠BAD=10°.
∴ ∠DAE=∠BAE-∠BAD=35°-10°=25°.
D
E
┐
B
A
C
典例精析
DIAN LI JING XI
例4
如图,在△ABC中,AD⊥BC,AE平分∠BAC(∠B>∠C). 若∠B=x°,
∠C=y°,求∠DAE(用x,y表示).
解:∵在△ABC中, ∠B=x°,∠C=y°,
∴∠BAC=(180-x-y)°.
∵AE平分∠BAC,
∴∠BAC=2∠BAE=2∠CAE.
∴∠BAE=90°-0.5(x+y)°.
∵AD⊥BC,∠B=80°, ∴∠BAD=(90-x)°.
∴ ∠DAE=∠BAE-∠BAD=0.5(x-y)°.
D
E
┐
B
A
C
从特殊到一般!
新知探究
XIN ZHI TAN JIU
从三角形的一个顶点向它的 所在的直线做垂线, 和
之间的 叫做三角形的高.
对边
顶点
垂足
线段
如图,在△ABC 中,AD⊥BC ,点D是垂足,
则 是△ABC的边BC上的高.
此时:_________________________.
A
B
C
D
AD
∠ADB = ∠ADC = 90°
注意:
标明垂直的记号和垂足的字母.
高的叙述方法(如图):有三种
新知探究
XIN ZHI TAN JIU
② AD⊥BC,垂足为 D.
③ 点 D 在 BC 上,且∠BDA =∠CDA = 90°.
① AD 是△ABC 的高.
A
B
C
D
新知探究
XIN ZHI TAN JIU
每一个三角形都有 个顶点,因此每一个三角形都有 条高.
如图,画出三角形的高.
3
3
这三条高之间有怎样的位置关系
锐角三角形的三条高是在三角形的内部还是外部
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
思考
思考
新知探究
XIN ZHI TAN JIU
思考
对于任意三角形,是否也满足“三条高相交于一点”
分别画出下列锐角三角形、直角三角形和钝角三角形的三条高,
并观察三条高是否相交于一点.
A
C
B
A
C
B
A
C
B
新知探究
XIN ZHI TAN JIU
(1)锐角三角形
O
A
B
C
D
E
F
①BC边上的高为
AC边上的高为
AB边上的高为
AD
BE
CF
②锐角三角形的三条高(线段AD、BE、CF) ,
且 .
相交于一点
该点位于三角形的内部
新知探究
XIN ZHI TAN JIU
(2)直角三角形
①AC边上的高为
直角边AB上的高为
直角边BC上的高为
BD
CB
AB
②直角三角形的三条高 .
相交于直角顶点
A
B
C
D
新知探究
XIN ZHI TAN JIU
(3)钝角三角形
A
B
C
D
E
F
①BC边上的高为
AB边上的高为
AC边上的高为
AD
CE
BF
②钝角三角形的三条高 .
不相交于一点
新知探究
XIN ZHI TAN JIU
思考
A
B
C
D
F
钝角三角形的三条高相交吗?
它们所在的直线交于一点吗?
这点位于何处?
O
E
钝角三角形的三条高不相交.
钝角三角形的三条高所在直线交于一点,
并且这个点在三角形外部.
思考
新知探究
XIN ZHI TAN JIU
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形
内部
直角顶点
三角形
外部
三角形三条高所在直线的交点称为三角形的 .
垂心
典例精析
DIAN LI JING XI
例5
下列各组图形中,哪一组图形中AD是△ABC的高( )
B
AD一定要垂直于三角形的另一条边.
典例精析
DIAN LI JING XI
例6
如图,在△ABC中,AC=8,BC=4,高BD=3,试作出BC边上的高AE,
并求AE的长.
解:如图,过点A作BC边上的高线AE,
交CB延长线于点E
∵BC AE= AC BD,AC=8,BC=4,高BD=3
∴ ×4AE= ×8×3
解得 AE=6
∴AE的长为6
E
课堂小结
QING JING YIN RU
三角形的中线
图形
几何语言
三角形中的重要线段
三角形的
角平分线
图形
几何语言
三角形的高线
图形
几何语言
∵AD是△ABC的高线.
∴AD⊥BC,∠ADB=∠ADC=90°
∵ AD是△ABC的BC上的中线
∴ BD=CD= BC
∵AD是△ABC的∠BAC的平分线
∴ ∠1=∠2= ∠BAC
当堂练习
QING JING YIN RU
1.如图,CM是△ABC的中线,AB=10cm,则BM的长为( )
A.7cm B.6cm
C.5cm D.4cm
C
2. 如图,在△ABC 中,∠ACB = 90°,CD⊥AB,图中线段
中可以作为△ABC 的高的有 ( )
A.2 条 B.3 条
C.4 条 D.5 条
B
当堂练习
QING JING YIN RU
3.填空:
(1) 如图①,AD,BE,CF 是△ABC 的三条中线,则
AB = 2__,BD = __,AE = __ .
(2) 如图②,AD,BE,CF 是△ABC 的三条角平分线,
则∠1 =_______, ∠3 =_______,∠ABC = 2_____.
图①
图②
AF
DC
∠CAD
∠2
∠BCF
A
B
C
D
E
F
AC
当堂练习
QING JING YIN RU
4.BD是△ABC的中线,AB=5,BC=3,求△ABD和△BCD的周长的差.
解:∵BD是△ABC的中线,
∴AD=CD,
∴△ABD和△BCD的周长的差
=(AB+BD+AD)-(BC+BD+CD)
=AB﹣BC,
∵AB=5,BC=3,
∴△ABD和△BCD的周长的差=5﹣3=2
当堂练习
QING JING YIN RU
解:∵ CD 是△ABC 的中线,
∴ BD = AD.
∵ BC - AC = 5cm,
∴△DBC 与△ADC 的周长差是 5 cm.
又∵△DBC 的周长为 25 cm,
∴△ADC 的周长为 25 - 5 = 20 (cm).
5. 如图,在△ABC 中,CD 是中线,已知 BC - AC = 5 cm, △DBC 的周长为 25 cm,求△ADC 的周长.
A
D
B
C
当堂练习
QING JING YIN RU
6.如图,在△ABC中,AB=AC,DB为△ABC的中线,且BD将△ABC周长分为12cm与15cm两部分,求三角形各边长.
解:∵DB为△ABC的中线
∴AD=CD
设AD=CD=x,则AB=2x
当x+2x=12,解得x=4
BC+x=15,解得BC=11
此时△ABC的三边长为:AB=AC=8,BC=11
当x+2x=15,BC+x=12,解得x=5,BC=7
此时△ABC的三边长为:AB=AC=10,BC=7
当堂练习
QING JING YIN RU
7. 如图所示,在△ABC 中,AB=AC=5,BC=6,AD⊥BC 于点 D,且 AD=4,若点 P 在边 AC 上移动,求 BP 的最小值.
解:根据垂线段最短,可知当 BP⊥AC 时,
BP 有最小值.
此时由△ABC 的面积公式可知,
AD · BC= BP · AC.
代入数值,可解得 BP= .
P
同课章节目录
