14.1全等三角形及其性质 课件(共23张PPT) 人教版(2024)数学八年级上册
文档属性
| 名称 | 14.1全等三角形及其性质 课件(共23张PPT) 人教版(2024)数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 39.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 16:20:07 | ||
图片预览




文档简介
(共23张PPT)
人教版 八年级上册
14.1
第十四章 全等三角形
全等三角形及其性质
情境引入
QING JING YIN RU
观察下面各组图形,说说他们有什么共同特点.
思考
情境引入
QING JING YIN RU
观察下面各组图形,说说他们有什么共同特点.
思考
新知探究
XIN ZHI TAN JIU
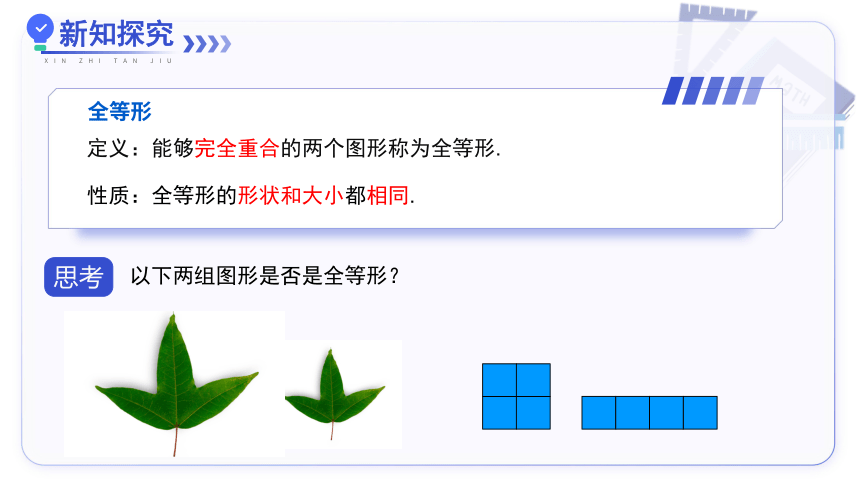
思考
以下两组图形是否是全等形?
全等形
定义:能够完全重合的两个图形称为全等形.
性质:全等形的形状和大小都相同.
典例精析
DIAN LI JING XI
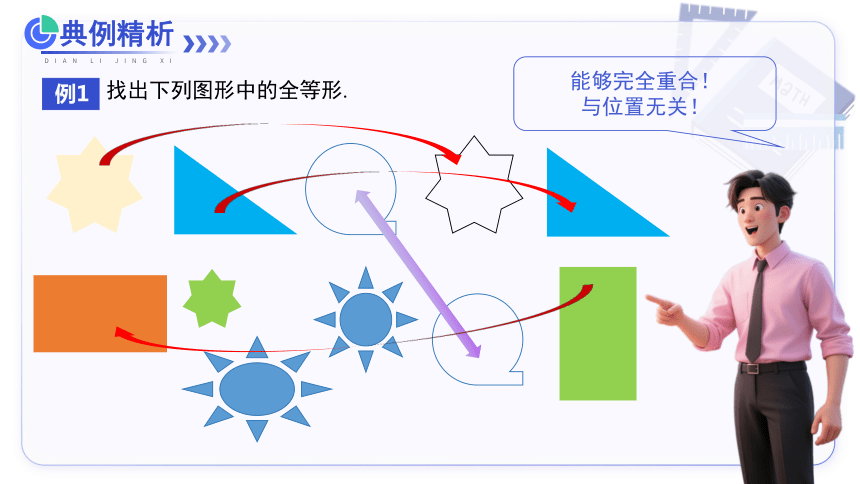
例1
找出下列图形中的全等形.
能够完全重合!
与位置无关!
典例精析
DIAN LI JING XI
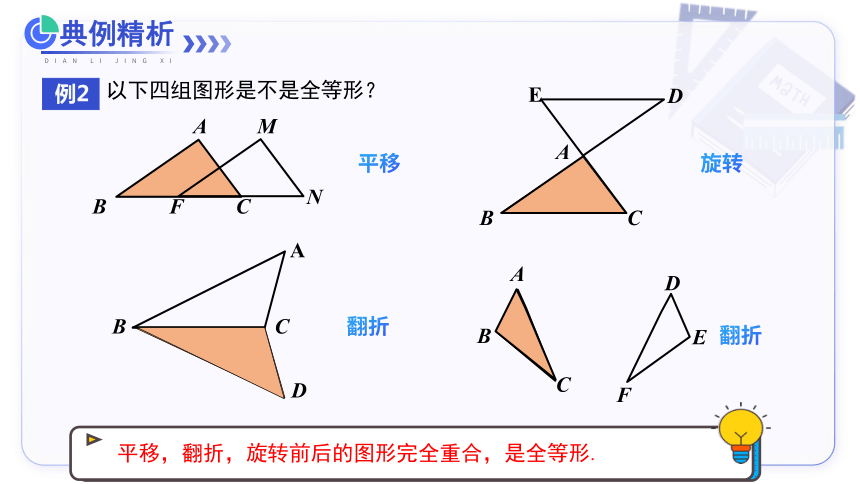
例2
以下四组图形是不是全等形?
A
A
C
B
D
E
A
B
C
D
C
F
N
M
B
A
B
D
C
E
F
平移
旋转
翻折
翻折
平移,翻折,旋转前后的图形完全重合,是全等形.
新知探究
XIN ZHI TAN JIU
全等三角形
能够完全重合的两个三角形叫
全等三角形的对应元素
全等三角形
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
B
C
A
E
F
D
点 A 和 ,点 B 和 ,点 C 和 是对应顶点.
AB 和 ,BC 和 ,AC 和 是对应边.
∠A 和 ,∠B 和 ,∠C 和 是对应角.
点 D
点 E
点 F
DE
EF
DF
∠D
∠E
∠F
对应顶点的字母写在对应的位置上
注
意
新知探究
XIN ZHI TAN JIU
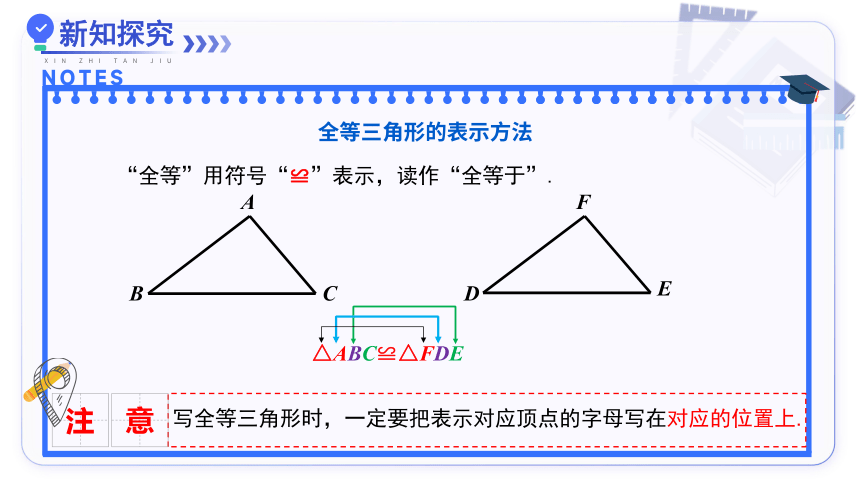
全等三角形的表示方法
△ABC≌△FDE
A
B
C
E
D
F
“全等”用符号“≌”表示,读作“全等于”.
写全等三角形时,一定要把表示对应顶点的字母写在对应的位置上.
注
意
典例精析
DIAN LI JING XI
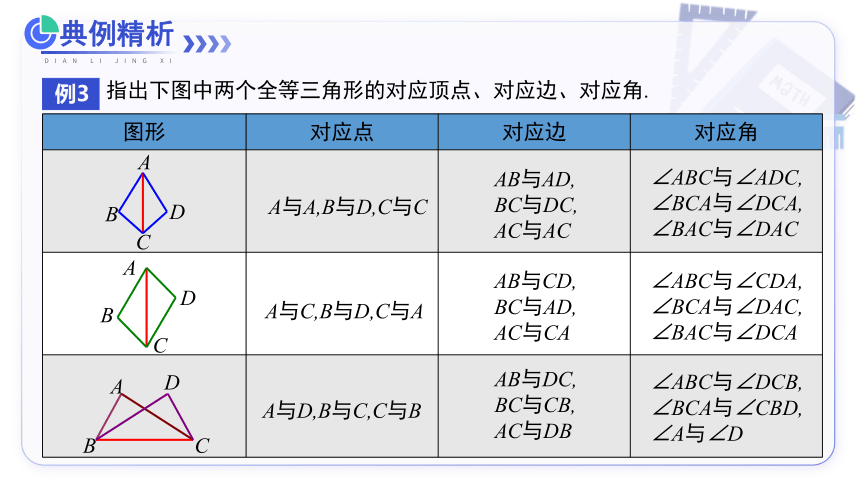
例3
指出下图中两个全等三角形的对应顶点、对应边、对应角.
图形 对应点 对应边 对应角
A
B
C
D
A
B
C
D
A
B
C
D
A与A,B与D,C与C
A与C,B与D,C与A
A与D,B与C,C与B
AB与AD,
BC与DC,
AC与AC
AB与CD,
BC与AD,
AC与CA
AB与DC,
BC与CB,
AC与DB
∠ABC与∠ADC,
∠BCA与∠DCA,
∠BAC与∠DAC
∠ABC与∠CDA,
∠BCA与∠DAC,
∠BAC与∠DCA
∠ABC与∠DCB,
∠BCA与∠CBD,
∠A与∠D
新知探究
XIN ZHI TAN JIU
思考
寻找对应边、对应角有什么规律
有公共边
有对顶角
有公共角
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
D
C
E
确定全等三角形对应元素的方法
①位置关系:不在同一直线上;②联接方式:首尾顺次相接.
新知探究
XIN ZHI TAN JIU
(1)根据书写规范,记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上,故可按照对应顶点的位置确定对应元素.如:△ABC△DEF,则AB和DE,AC和DF,BC和EF是对应边,∠A和∠D,∠B和∠E,∠C和∠F是对应角.
(2)图形位置法:①公共边一定是对应边;②公共角一定是对应角;
③对顶角一定是对应角.
(3)图形大小法:最大边与最大边(最小边与最小边)为对应边;最大角与最大角(最小角与最小角)为对应角; 对应角的对边为对应边;对应边的对角为对应角.
新知探究
XIN ZHI TAN JIU
练习
找一找下列全等图形的对应元素:
A
D
F
C
E
B
1
2
E
A
B
C
F
1
2
3
4
A
B
C
D
F
A
B
D
C
1
4
2
3
对应边和对应角
新知探究
XIN ZHI TAN JIU
全等三角形的几何语言
∵△ABC≌△FDE,
∴ AB = FD,AC = FE,BC = DE (全等三角形的对应边相等),
∠A =∠F,∠B =∠D,∠C =∠E (全等三角形对应角相等).
A
B
C
E
D
F
对应!!!
典例精析
DIAN LI JING XI
例4
解:(1)
对应边:AB 和 AC,AD 和 AE,BD 和 CE.
对应角:∠A 和 ∠A,∠ABD 和 ∠ACE,∠ADB 和 ∠AEC.
如图,△AEC△ADB,点E和点D是对应顶点.
(1)写出它们的对应边和对应角;
(2)若∠A=50°,∠ABD=39°,且∠1=∠2,求∠1的度数.
(2)∵△AEC ≌ △ADB,∴∠ACE = ∠ABD = 39°.
在△ABC 中,∠A +∠ABC +∠ACB = 180°,
即∠A +∠ABD +∠1 +∠2 +∠ACE = 180°.
又∵∠1=∠2,
∴ 50°+ 39°+ 2∠1 + 39°= 180°,解得∠1 = 26°.
典例精析
DIAN LI JING XI
例5
已知:如图,△ABC ≌△DEF.
(1)若DF =10 cm,则AC 的长为 ;
(2)若∠A =100°,则∠D 的度数为 ;
10 cm
100°
A
B
C
D
E
F
全等三角形的对应边相等,对应角相等!
典例精析
DIAN LI JING XI
例6
解:OC=OB,OA=OD,CA=BD,
∠COA=∠BOD,∠C=∠B,∠A=∠D.
∠B=∠C=180°-∠A-∠AOC=85°.
利用全等三角形的对应角相等转化为∠C
如图,△OCA≌△OBD,C和B,A和D是对应顶点,说出这两个三角形中相等的边和角.若∠A=20°,∠AOC=75°,你能求出∠B的度数吗?
典例精析
DIAN LI JING XI
例7
解:AB = AC,AE = AD,BE =CD,∠BAE =∠CAD.
DC = BE = BD+DE = 5cm.
利用全等三角形的对应角相等转化为BE
如图,已知△ABE≌△ACD,∠ADE=∠AED,∠B=∠C,指出其他的对应边和对应角.若BD=2cm,DE=3cm,你能求出DC的长吗?
典例精析
DIAN LI JING XI
常见的全等三角形重要模型总结
课堂小结
QING JING YIN RU
对应元素确定方法
能够完全重合的两个三角形叫做全等三角形
对应边
对应角
定义
全等
三角形
基本性质
对应边相等
对应角相等
长对长,短对短,中对中
公共边一定是对应边
大角对大角,小角对小角
公共角一定是对应角
对顶角一定是对应角
定义:能够完全重合的两个图形称为全等形.
当堂练习
QING JING YIN RU
1. 下列说法正确的是( )
A. 两个面积相等的图形一定是全等形
B. 两个长方形是全等形
C. 两个全等图形的形状一定相同
D. 两个正方形一定是全等形
C
A
根据三角形的内角和,只能是∠A=100°
2.在△ABC中,∠B = ∠C,与△ABC全等的三角形有一个角是100°,那么在△ABC中与100°角对应相等的角是( )
A.∠A B.∠B
C.∠C D.∠B或∠C
当堂练习
QING JING YIN RU
C
D
C
B
O
A
D
并非对应角,不一定相等
3.如图所示,△ABD≌△CDB,下面四个结论中,不正确的是( )
A.△ABD和△CDB的面积相等
B.△ABD和△CDB的周长相等
C.∠A+∠ABD =∠C +∠CBD
D.AD∥BC,且AD = BC
并非对应边,不一定相等
4.如图,△OCA ≌△OBD,点C 和点B,点A与点D是对应点,则下列结论错误的是( )
A. ∠COA =∠BOD
B. ∠A =∠D
C. CA =BD
D. OB =OA
当堂练习
QING JING YIN RU
5.△ABN ≌△ACM, ∠ABN 和∠ACM 是对应角,AB 和AC 是对应边.则下列结论错误的是( )
A.∠AMC =∠ANB
B.∠BAN =∠CAM
C.BM =MN
D.AM =AN
C
A
B
C
M
N
6.如图,△ABC≌△ADE,则AB = ___ ,∠E = _____.
若∠BAE = 120°,∠BAD = 40°,则∠BAC = _______.
AD
∠C
80°
当堂练习
QING JING YIN RU
7.如图,△EFG≌△NMH,EF = 2.1 cm,EH = 1.1 cm,NH = 3.3 cm.
(1)试写出两三角形的对应边、对应角;(2)求线段 NM 及 HG 的长度;
(3)观察图形中对应线段的数量或位置关系,试提出一个正确的结论并说明理由.
解:(1)对应边有 EF 和 NM,FG 和 MH,EG 和 NH;
对应角有∠E 和∠N,∠F 和∠M,∠EGF 和∠NHM.
(2)∵ △EFG≌△NMH, ∴ EF = NM = 2.1 cm,
EG = NH = 3.3 cm.
∴ HG = EG - EH = 3.3 - 1.1 = 2.2 (cm).
(3)结论:EF∥NM (答案不唯一).
理由:∵ △EFG≌△NMH,
∴∠E =∠N. ∴ EF∥NM.
人教版 八年级上册
14.1
第十四章 全等三角形
全等三角形及其性质
情境引入
QING JING YIN RU
观察下面各组图形,说说他们有什么共同特点.
思考
情境引入
QING JING YIN RU
观察下面各组图形,说说他们有什么共同特点.
思考
新知探究
XIN ZHI TAN JIU
思考
以下两组图形是否是全等形?
全等形
定义:能够完全重合的两个图形称为全等形.
性质:全等形的形状和大小都相同.
典例精析
DIAN LI JING XI
例1
找出下列图形中的全等形.
能够完全重合!
与位置无关!
典例精析
DIAN LI JING XI
例2
以下四组图形是不是全等形?
A
A
C
B
D
E
A
B
C
D
C
F
N
M
B
A
B
D
C
E
F
平移
旋转
翻折
翻折
平移,翻折,旋转前后的图形完全重合,是全等形.
新知探究
XIN ZHI TAN JIU
全等三角形
能够完全重合的两个三角形叫
全等三角形的对应元素
全等三角形
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
B
C
A
E
F
D
点 A 和 ,点 B 和 ,点 C 和 是对应顶点.
AB 和 ,BC 和 ,AC 和 是对应边.
∠A 和 ,∠B 和 ,∠C 和 是对应角.
点 D
点 E
点 F
DE
EF
DF
∠D
∠E
∠F
对应顶点的字母写在对应的位置上
注
意
新知探究
XIN ZHI TAN JIU
全等三角形的表示方法
△ABC≌△FDE
A
B
C
E
D
F
“全等”用符号“≌”表示,读作“全等于”.
写全等三角形时,一定要把表示对应顶点的字母写在对应的位置上.
注
意
典例精析
DIAN LI JING XI
例3
指出下图中两个全等三角形的对应顶点、对应边、对应角.
图形 对应点 对应边 对应角
A
B
C
D
A
B
C
D
A
B
C
D
A与A,B与D,C与C
A与C,B与D,C与A
A与D,B与C,C与B
AB与AD,
BC与DC,
AC与AC
AB与CD,
BC与AD,
AC与CA
AB与DC,
BC与CB,
AC与DB
∠ABC与∠ADC,
∠BCA与∠DCA,
∠BAC与∠DAC
∠ABC与∠CDA,
∠BCA与∠DAC,
∠BAC与∠DCA
∠ABC与∠DCB,
∠BCA与∠CBD,
∠A与∠D
新知探究
XIN ZHI TAN JIU
思考
寻找对应边、对应角有什么规律
有公共边
有对顶角
有公共角
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
D
C
E
确定全等三角形对应元素的方法
①位置关系:不在同一直线上;②联接方式:首尾顺次相接.
新知探究
XIN ZHI TAN JIU
(1)根据书写规范,记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上,故可按照对应顶点的位置确定对应元素.如:△ABC△DEF,则AB和DE,AC和DF,BC和EF是对应边,∠A和∠D,∠B和∠E,∠C和∠F是对应角.
(2)图形位置法:①公共边一定是对应边;②公共角一定是对应角;
③对顶角一定是对应角.
(3)图形大小法:最大边与最大边(最小边与最小边)为对应边;最大角与最大角(最小角与最小角)为对应角; 对应角的对边为对应边;对应边的对角为对应角.
新知探究
XIN ZHI TAN JIU
练习
找一找下列全等图形的对应元素:
A
D
F
C
E
B
1
2
E
A
B
C
F
1
2
3
4
A
B
C
D
F
A
B
D
C
1
4
2
3
对应边和对应角
新知探究
XIN ZHI TAN JIU
全等三角形的几何语言
∵△ABC≌△FDE,
∴ AB = FD,AC = FE,BC = DE (全等三角形的对应边相等),
∠A =∠F,∠B =∠D,∠C =∠E (全等三角形对应角相等).
A
B
C
E
D
F
对应!!!
典例精析
DIAN LI JING XI
例4
解:(1)
对应边:AB 和 AC,AD 和 AE,BD 和 CE.
对应角:∠A 和 ∠A,∠ABD 和 ∠ACE,∠ADB 和 ∠AEC.
如图,△AEC△ADB,点E和点D是对应顶点.
(1)写出它们的对应边和对应角;
(2)若∠A=50°,∠ABD=39°,且∠1=∠2,求∠1的度数.
(2)∵△AEC ≌ △ADB,∴∠ACE = ∠ABD = 39°.
在△ABC 中,∠A +∠ABC +∠ACB = 180°,
即∠A +∠ABD +∠1 +∠2 +∠ACE = 180°.
又∵∠1=∠2,
∴ 50°+ 39°+ 2∠1 + 39°= 180°,解得∠1 = 26°.
典例精析
DIAN LI JING XI
例5
已知:如图,△ABC ≌△DEF.
(1)若DF =10 cm,则AC 的长为 ;
(2)若∠A =100°,则∠D 的度数为 ;
10 cm
100°
A
B
C
D
E
F
全等三角形的对应边相等,对应角相等!
典例精析
DIAN LI JING XI
例6
解:OC=OB,OA=OD,CA=BD,
∠COA=∠BOD,∠C=∠B,∠A=∠D.
∠B=∠C=180°-∠A-∠AOC=85°.
利用全等三角形的对应角相等转化为∠C
如图,△OCA≌△OBD,C和B,A和D是对应顶点,说出这两个三角形中相等的边和角.若∠A=20°,∠AOC=75°,你能求出∠B的度数吗?
典例精析
DIAN LI JING XI
例7
解:AB = AC,AE = AD,BE =CD,∠BAE =∠CAD.
DC = BE = BD+DE = 5cm.
利用全等三角形的对应角相等转化为BE
如图,已知△ABE≌△ACD,∠ADE=∠AED,∠B=∠C,指出其他的对应边和对应角.若BD=2cm,DE=3cm,你能求出DC的长吗?
典例精析
DIAN LI JING XI
常见的全等三角形重要模型总结
课堂小结
QING JING YIN RU
对应元素确定方法
能够完全重合的两个三角形叫做全等三角形
对应边
对应角
定义
全等
三角形
基本性质
对应边相等
对应角相等
长对长,短对短,中对中
公共边一定是对应边
大角对大角,小角对小角
公共角一定是对应角
对顶角一定是对应角
定义:能够完全重合的两个图形称为全等形.
当堂练习
QING JING YIN RU
1. 下列说法正确的是( )
A. 两个面积相等的图形一定是全等形
B. 两个长方形是全等形
C. 两个全等图形的形状一定相同
D. 两个正方形一定是全等形
C
A
根据三角形的内角和,只能是∠A=100°
2.在△ABC中,∠B = ∠C,与△ABC全等的三角形有一个角是100°,那么在△ABC中与100°角对应相等的角是( )
A.∠A B.∠B
C.∠C D.∠B或∠C
当堂练习
QING JING YIN RU
C
D
C
B
O
A
D
并非对应角,不一定相等
3.如图所示,△ABD≌△CDB,下面四个结论中,不正确的是( )
A.△ABD和△CDB的面积相等
B.△ABD和△CDB的周长相等
C.∠A+∠ABD =∠C +∠CBD
D.AD∥BC,且AD = BC
并非对应边,不一定相等
4.如图,△OCA ≌△OBD,点C 和点B,点A与点D是对应点,则下列结论错误的是( )
A. ∠COA =∠BOD
B. ∠A =∠D
C. CA =BD
D. OB =OA
当堂练习
QING JING YIN RU
5.△ABN ≌△ACM, ∠ABN 和∠ACM 是对应角,AB 和AC 是对应边.则下列结论错误的是( )
A.∠AMC =∠ANB
B.∠BAN =∠CAM
C.BM =MN
D.AM =AN
C
A
B
C
M
N
6.如图,△ABC≌△ADE,则AB = ___ ,∠E = _____.
若∠BAE = 120°,∠BAD = 40°,则∠BAC = _______.
AD
∠C
80°
当堂练习
QING JING YIN RU
7.如图,△EFG≌△NMH,EF = 2.1 cm,EH = 1.1 cm,NH = 3.3 cm.
(1)试写出两三角形的对应边、对应角;(2)求线段 NM 及 HG 的长度;
(3)观察图形中对应线段的数量或位置关系,试提出一个正确的结论并说明理由.
解:(1)对应边有 EF 和 NM,FG 和 MH,EG 和 NH;
对应角有∠E 和∠N,∠F 和∠M,∠EGF 和∠NHM.
(2)∵ △EFG≌△NMH, ∴ EF = NM = 2.1 cm,
EG = NH = 3.3 cm.
∴ HG = EG - EH = 3.3 - 1.1 = 2.2 (cm).
(3)结论:EF∥NM (答案不唯一).
理由:∵ △EFG≌△NMH,
∴∠E =∠N. ∴ EF∥NM.
同课章节目录
