14.2(第4课时)尺规作图问题 课件(共19张PPT) 人教版(2024)数学八年级上册
文档属性
| 名称 | 14.2(第4课时)尺规作图问题 课件(共19张PPT) 人教版(2024)数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 32.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 16:20:58 | ||
图片预览


文档简介
(共19张PPT)
人教版 八年级上册
14.2(第4课时)
第十四章 全等三角形
尺规作图问题
复习回顾
FU XI HUI GU
思考
基本事实:两边和它们的夹角分别相等的两个三角形全等,
简写成“边角边”或“SAS”.
前面我们学习过哪些判定三角形全等的方法?
基本事实:有两角和它们的夹边分别相等的两个三角形全等,
简写成“角边角”或“ASA”.
基本事实:两角和其中一角的对边分别相等的两个三角形全等,
简写成“角角边”或“AAS”.
基本事实:三边分别相等的两个三角形全等.
简记为“边边边”或“SSS”.
新知探究
XIN ZHI TAN JIU
思考
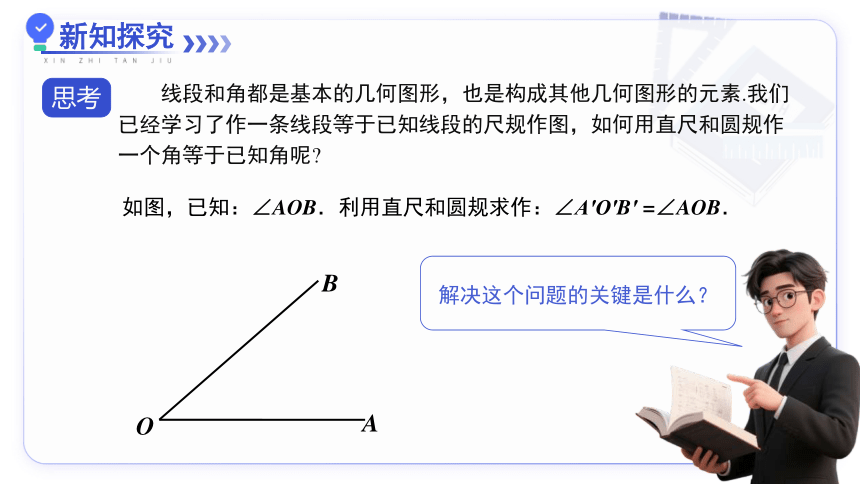
线段和角都是基本的几何图形,也是构成其他几何图形的元素.我们已经学习了作一条线段等于已知线段的尺规作图,如何用直尺和圆规作一个角等于已知角呢
如图,已知:∠AOB.利用直尺和圆规求作:∠A′O′B′ =∠AOB.
O
B
A
解决这个问题的关键是什么?
新知探究
XIN ZHI TAN JIU
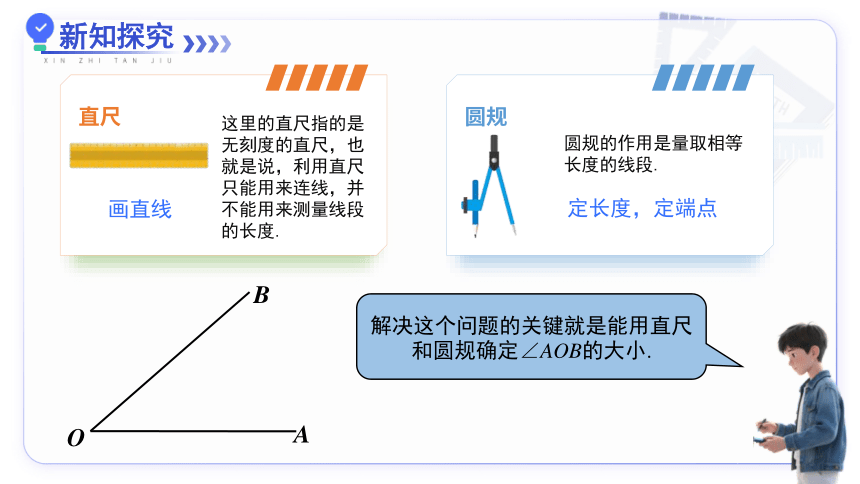
圆规的作用是量取相等长度的线段.
圆规
定长度,定端点
这里的直尺指的是无刻度的直尺,也就是说,利用直尺只能用来连线,并不能用来测量线段的长度.
直尺
画直线
O
B
A
解决这个问题的关键就是能用直尺和圆规确定∠AOB的大小.
新知探究
XIN ZHI TAN JIU
思考
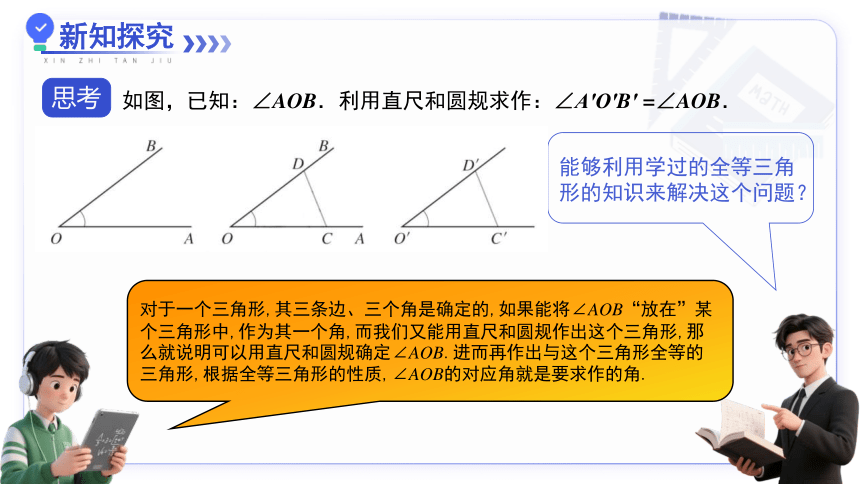
如图,已知:∠AOB.利用直尺和圆规求作:∠A′O′B′ =∠AOB.
能够利用学过的全等三角形的知识来解决这个问题?
对于一个三角形,其三条边、三个角是确定的,如果能将∠AOB“放在”某个三角形中,作为其一个角,而我们又能用直尺和圆规作出这个三角形,那么就说明可以用直尺和圆规确定∠AOB.进而再作出与这个三角形全等的三角形,根据全等三角形的性质,∠AOB的对应角就是要求作的角.
新知探究
XIN ZHI TAN JIU
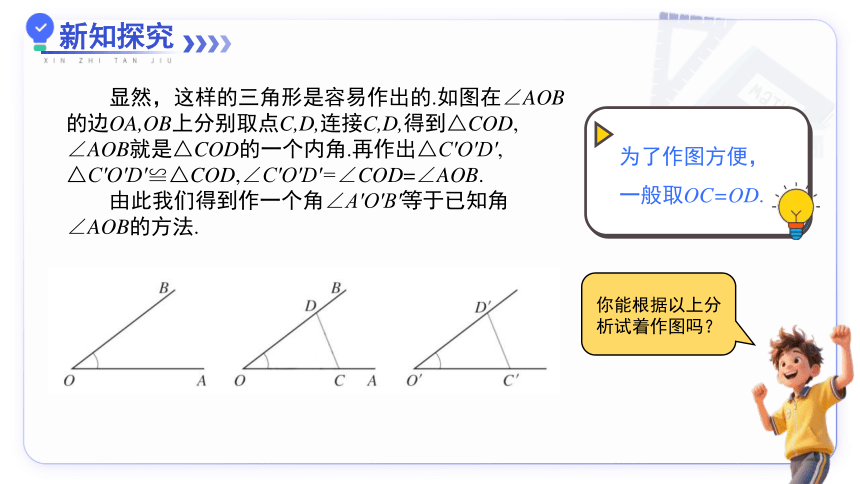
显然,这样的三角形是容易作出的.如图在∠AOB的边OA,OB上分别取点C,D,连接C,D,得到△COD,
∠AOB就是△COD的一个内角.再作出△C′O′D′,
△C′O′D′≌△COD,∠C′O′D′=∠COD=∠AOB.
由此我们得到作一个角∠A′O'B'等于已知角∠AOB的方法.
为了作图方便,
一般取OC=OD.
你能根据以上分析试着作图吗?
新知探究
XIN ZHI TAN JIU
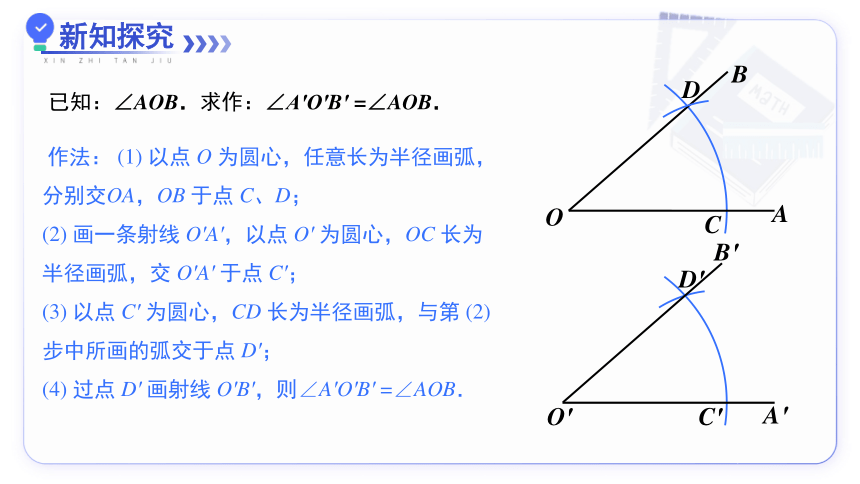
作法: (1) 以点 O 为圆心,任意长为半径画弧,
分别交OA,OB 于点 C、D;
(2) 画一条射线 O′A′,以点 O′ 为圆心,OC 长为
半径画弧,交 O′A′ 于点 C′;
(3) 以点 C′ 为圆心,CD 长为半径画弧,与第 (2)
步中所画的弧交于点 D′;
(4) 过点 D′ 画射线 O′B′,则∠A′O′B′ =∠AOB.
已知:∠AOB.求作:∠A′O′B′ =∠AOB.
O
D
B
C
A
O′
C′
A′
B′
D′
新知探究
XIN ZHI TAN JIU
思考
你能证明以上作图的正确性吗?
DO= D’O’(已知),
OC = O’C ’(已知),
DC = D’C ’ (已知),
∴△DOC≌△D’O’C ’ (SSS).
证明:在△DOC 和△D’O’C ’中,
∴∠O=∠O’ (全等三角形的对应角相等).
O
D
B
C
A
O′
C′
A′
B′
D′
新知探究
XIN ZHI TAN JIU
探究
已知: ∠AOB. 求作: ∠A′O′B ′, 使∠A′O′B′=2∠AOB.
B
O
A
D
C
D′
C′
B ′
O ′
A′
就是作一个角等于已知角的二倍
可以理解为作一个角等于已知角,作两次!
典例精析
DIAN LI JING XI
例1
分析:我们知道,同位角相等,两直线平行.可以利用这个结论,过点C作直线AB的平行线CD.为此需要先作出截线,再作出相等的同位角.
如图,已知直线AB及直线AB外一点C.利用直尺和圆规过点C作直线AB的
平行线CD.
解:(1)过点C作一条直线,与直线AB相交于点E;
(2)在点C处作∠CEB的同位角∠FCD,使∠FCD=∠CEB;
(3)反向延长CD,得直线CD,则直线CD//AB.
F
B
A
C
B
A
C
E
还可以利用“内错角相等,两直线平行”作图.
典例精析
DIAN LI JING XI
例2
就是作一个角等于已知角.
如图,已知线段a,b和∠α,求作△ABC,使AB=a,AC=b,∠A=∠α.
作法:如图.
(1)作∠DAE=∠α;
(2)在射线AD上作AB=a,在射线AE上作AC=b;
(3)连接BC,则△ABC就是所求作的三角形.
C
A
B
b
a
α
b
a
)
D
E
典例精析
DIAN LI JING XI
例3
作法:
(1) 作∠DAF=∠α;
(2) 在射线AF上截取线段AB=c;
(3)以B为顶点,以BA为一边,作∠ABE=∠β,
BE交AD于点C,则△ABC就是所求作的三角形.
c
α
β
已知: ∠α , ∠β,线段c.
求作:△ABC,使∠A=∠α,∠B=∠β ,AB=c
A
F
D
B
C
E
分析:因为未被墨水污染的有两角及其夹边,所以根据“ASA”可以作一个与原三角形全等的三角形.
典例精析
DIAN LI JING XI
例4
如图所示,果果在作业本上画的三角形被墨水污染,他想画一个与原来完全一样的三角形,请你帮帮他.
A
B
C
课堂小结
QING JING YIN RU
基本类型
尺规作图
作一个角等于已知角
利用“SSS”
证明全等
已知:写出符合题意的已知
求作:写出所要作的三角形及符合的条件
作法:按照尺规作图,作出符合题意的三角形
基本步骤
已知三边
已知两边及其夹角
已知两角及其中一角的对边
拓展类型
已知两角及其夹边
“边边角”不能证明全等,角只能是两边的夹角!
只允许用无刻度直尺和圆规,
不能使用其测量的功能.
当堂练习
QING JING YIN RU
1. 下列属于尺规作图的是( )
A. 用刻度尺和圆规作△ABC
B. 用量角器画一个300°的角
C. 用圆规画半径2cm的圆
D. 作一条线段等于已知线段
D
2. 利用尺规不能唯一作出的三角形是( )
A. 已知三边 B. 已知两边及夹角
C. 已知两角及夹边 D. 已知两边及其中一边的对角
D
实例上是【例1】中利用“内错角相等,两直线平行”作图.
即判断能否利用已知条件判定三角形全等.
当堂练习
QING JING YIN RU
3.根据下列已知条件,能唯一画出△ABC的是( ).
A. ∠A=36°,∠B=45°,AB=4
B. AB=4,BC=3,∠A=30°
C. AB=3,BC=4,CA=1
D. ∠C=90°,AB=6
A
4.如图,用尺规作出∠OBF=∠AOB,作图痕迹MN是( ).
A. 以点B为圆心,OD为半径的弧
B. 以点B为圆心,DC为半径的弧
C. 以点E为圆心,OD为半径的弧
D. 以点E为圆心,DC为半径的弧
D
O
C
D
E
M
F
N
B
A
当堂练习
QING JING YIN RU
5. 已知: ∠α,∠β,其中∠α >∠β. 求作:∠AOB,使∠AOB= ∠α -∠β.
解:如图所示,作法如下:
(1)作∠AOD,使∠AOD=∠α;
(2)作∠BOD,使∠BOD=∠β,
并且使射线OB落在∠AOD的内部.
则∠AOB就是所要求作的角.
E
F
M
N
D
C
B
A
O
当堂练习
QING JING YIN RU
6.已知线段 a,b,求作△ABC,使AB=AC=a,BC=b.
b
a
解:
第一步:作射线BM,在BM上截取BC=b.
第二步:分别以B,C为圆心,以 a 为半径画弧,两弧交于点A.
第三步:连接AC,AB. 则△ABC为所求作的三角形.
b
B
M
C
A
a
a
当堂练习
QING JING YIN RU
a
b
7. 已知:直角,线段a,b.
求作:直角三角形ABC,使BC=a,AC=b.
C
D
E
B
A
作法:
(1)作∠DCE=90°;
(2)在射线CD、CE上分别
截取CB=a,CA=b ;
(3)连结AB. △ABC就是所求作的三角形.
人教版 八年级上册
14.2(第4课时)
第十四章 全等三角形
尺规作图问题
复习回顾
FU XI HUI GU
思考
基本事实:两边和它们的夹角分别相等的两个三角形全等,
简写成“边角边”或“SAS”.
前面我们学习过哪些判定三角形全等的方法?
基本事实:有两角和它们的夹边分别相等的两个三角形全等,
简写成“角边角”或“ASA”.
基本事实:两角和其中一角的对边分别相等的两个三角形全等,
简写成“角角边”或“AAS”.
基本事实:三边分别相等的两个三角形全等.
简记为“边边边”或“SSS”.
新知探究
XIN ZHI TAN JIU
思考
线段和角都是基本的几何图形,也是构成其他几何图形的元素.我们已经学习了作一条线段等于已知线段的尺规作图,如何用直尺和圆规作一个角等于已知角呢
如图,已知:∠AOB.利用直尺和圆规求作:∠A′O′B′ =∠AOB.
O
B
A
解决这个问题的关键是什么?
新知探究
XIN ZHI TAN JIU
圆规的作用是量取相等长度的线段.
圆规
定长度,定端点
这里的直尺指的是无刻度的直尺,也就是说,利用直尺只能用来连线,并不能用来测量线段的长度.
直尺
画直线
O
B
A
解决这个问题的关键就是能用直尺和圆规确定∠AOB的大小.
新知探究
XIN ZHI TAN JIU
思考
如图,已知:∠AOB.利用直尺和圆规求作:∠A′O′B′ =∠AOB.
能够利用学过的全等三角形的知识来解决这个问题?
对于一个三角形,其三条边、三个角是确定的,如果能将∠AOB“放在”某个三角形中,作为其一个角,而我们又能用直尺和圆规作出这个三角形,那么就说明可以用直尺和圆规确定∠AOB.进而再作出与这个三角形全等的三角形,根据全等三角形的性质,∠AOB的对应角就是要求作的角.
新知探究
XIN ZHI TAN JIU
显然,这样的三角形是容易作出的.如图在∠AOB的边OA,OB上分别取点C,D,连接C,D,得到△COD,
∠AOB就是△COD的一个内角.再作出△C′O′D′,
△C′O′D′≌△COD,∠C′O′D′=∠COD=∠AOB.
由此我们得到作一个角∠A′O'B'等于已知角∠AOB的方法.
为了作图方便,
一般取OC=OD.
你能根据以上分析试着作图吗?
新知探究
XIN ZHI TAN JIU
作法: (1) 以点 O 为圆心,任意长为半径画弧,
分别交OA,OB 于点 C、D;
(2) 画一条射线 O′A′,以点 O′ 为圆心,OC 长为
半径画弧,交 O′A′ 于点 C′;
(3) 以点 C′ 为圆心,CD 长为半径画弧,与第 (2)
步中所画的弧交于点 D′;
(4) 过点 D′ 画射线 O′B′,则∠A′O′B′ =∠AOB.
已知:∠AOB.求作:∠A′O′B′ =∠AOB.
O
D
B
C
A
O′
C′
A′
B′
D′
新知探究
XIN ZHI TAN JIU
思考
你能证明以上作图的正确性吗?
DO= D’O’(已知),
OC = O’C ’(已知),
DC = D’C ’ (已知),
∴△DOC≌△D’O’C ’ (SSS).
证明:在△DOC 和△D’O’C ’中,
∴∠O=∠O’ (全等三角形的对应角相等).
O
D
B
C
A
O′
C′
A′
B′
D′
新知探究
XIN ZHI TAN JIU
探究
已知: ∠AOB. 求作: ∠A′O′B ′, 使∠A′O′B′=2∠AOB.
B
O
A
D
C
D′
C′
B ′
O ′
A′
就是作一个角等于已知角的二倍
可以理解为作一个角等于已知角,作两次!
典例精析
DIAN LI JING XI
例1
分析:我们知道,同位角相等,两直线平行.可以利用这个结论,过点C作直线AB的平行线CD.为此需要先作出截线,再作出相等的同位角.
如图,已知直线AB及直线AB外一点C.利用直尺和圆规过点C作直线AB的
平行线CD.
解:(1)过点C作一条直线,与直线AB相交于点E;
(2)在点C处作∠CEB的同位角∠FCD,使∠FCD=∠CEB;
(3)反向延长CD,得直线CD,则直线CD//AB.
F
B
A
C
B
A
C
E
还可以利用“内错角相等,两直线平行”作图.
典例精析
DIAN LI JING XI
例2
就是作一个角等于已知角.
如图,已知线段a,b和∠α,求作△ABC,使AB=a,AC=b,∠A=∠α.
作法:如图.
(1)作∠DAE=∠α;
(2)在射线AD上作AB=a,在射线AE上作AC=b;
(3)连接BC,则△ABC就是所求作的三角形.
C
A
B
b
a
α
b
a
)
D
E
典例精析
DIAN LI JING XI
例3
作法:
(1) 作∠DAF=∠α;
(2) 在射线AF上截取线段AB=c;
(3)以B为顶点,以BA为一边,作∠ABE=∠β,
BE交AD于点C,则△ABC就是所求作的三角形.
c
α
β
已知: ∠α , ∠β,线段c.
求作:△ABC,使∠A=∠α,∠B=∠β ,AB=c
A
F
D
B
C
E
分析:因为未被墨水污染的有两角及其夹边,所以根据“ASA”可以作一个与原三角形全等的三角形.
典例精析
DIAN LI JING XI
例4
如图所示,果果在作业本上画的三角形被墨水污染,他想画一个与原来完全一样的三角形,请你帮帮他.
A
B
C
课堂小结
QING JING YIN RU
基本类型
尺规作图
作一个角等于已知角
利用“SSS”
证明全等
已知:写出符合题意的已知
求作:写出所要作的三角形及符合的条件
作法:按照尺规作图,作出符合题意的三角形
基本步骤
已知三边
已知两边及其夹角
已知两角及其中一角的对边
拓展类型
已知两角及其夹边
“边边角”不能证明全等,角只能是两边的夹角!
只允许用无刻度直尺和圆规,
不能使用其测量的功能.
当堂练习
QING JING YIN RU
1. 下列属于尺规作图的是( )
A. 用刻度尺和圆规作△ABC
B. 用量角器画一个300°的角
C. 用圆规画半径2cm的圆
D. 作一条线段等于已知线段
D
2. 利用尺规不能唯一作出的三角形是( )
A. 已知三边 B. 已知两边及夹角
C. 已知两角及夹边 D. 已知两边及其中一边的对角
D
实例上是【例1】中利用“内错角相等,两直线平行”作图.
即判断能否利用已知条件判定三角形全等.
当堂练习
QING JING YIN RU
3.根据下列已知条件,能唯一画出△ABC的是( ).
A. ∠A=36°,∠B=45°,AB=4
B. AB=4,BC=3,∠A=30°
C. AB=3,BC=4,CA=1
D. ∠C=90°,AB=6
A
4.如图,用尺规作出∠OBF=∠AOB,作图痕迹MN是( ).
A. 以点B为圆心,OD为半径的弧
B. 以点B为圆心,DC为半径的弧
C. 以点E为圆心,OD为半径的弧
D. 以点E为圆心,DC为半径的弧
D
O
C
D
E
M
F
N
B
A
当堂练习
QING JING YIN RU
5. 已知: ∠α,∠β,其中∠α >∠β. 求作:∠AOB,使∠AOB= ∠α -∠β.
解:如图所示,作法如下:
(1)作∠AOD,使∠AOD=∠α;
(2)作∠BOD,使∠BOD=∠β,
并且使射线OB落在∠AOD的内部.
则∠AOB就是所要求作的角.
E
F
M
N
D
C
B
A
O
当堂练习
QING JING YIN RU
6.已知线段 a,b,求作△ABC,使AB=AC=a,BC=b.
b
a
解:
第一步:作射线BM,在BM上截取BC=b.
第二步:分别以B,C为圆心,以 a 为半径画弧,两弧交于点A.
第三步:连接AC,AB. 则△ABC为所求作的三角形.
b
B
M
C
A
a
a
当堂练习
QING JING YIN RU
a
b
7. 已知:直角,线段a,b.
求作:直角三角形ABC,使BC=a,AC=b.
C
D
E
B
A
作法:
(1)作∠DCE=90°;
(2)在射线CD、CE上分别
截取CB=a,CA=b ;
(3)连结AB. △ABC就是所求作的三角形.
同课章节目录
