14.2(第3课时)边边边 课件(共21张PPT) 人教版(2024)数学八年级上册
文档属性
| 名称 | 14.2(第3课时)边边边 课件(共21张PPT) 人教版(2024)数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 30.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 16:21:37 | ||
图片预览


文档简介
(共21张PPT)
人教版 八年级上册
14.2(第3课时)
第十四章 全等三角形
边边边
复习回顾
FU XI HUI GU
思考
基本事实:两边和它们的夹角分别相等的两个三角形全等,
简写成“边角边”或“SAS”.
前面我们学习过哪些判定三角形全等的方法?
基本事实:有两角和它们的夹边分别相等的两个三角形全等,
简写成“角边角”或“ASA”.
基本事实:两角和其中一角的对边分别相等的两个三角形全等,
简写成“角角边”或“AAS”.
前面我们研究了两个三角形的两边和一角分别相等的情况以及两角和一边分别相等的情况.接下来研究三边分别相等的情况.
新知探究
XIN ZHI TAN JIU
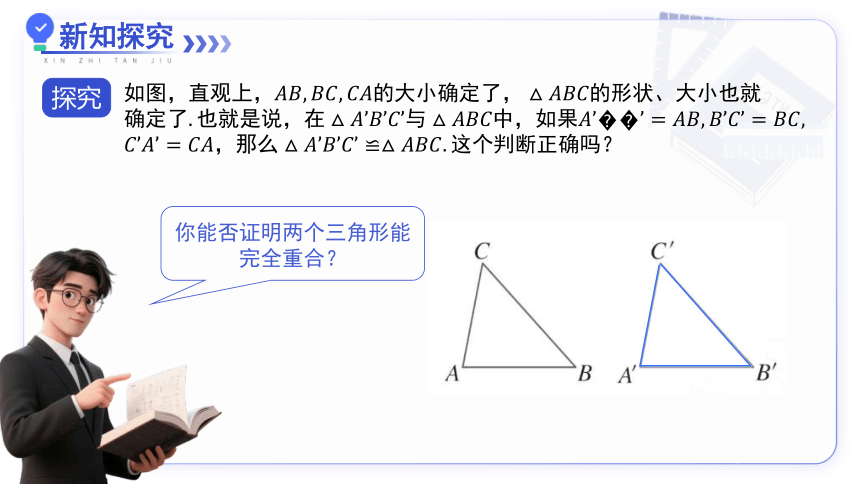
探究
你能否证明两个三角形能完全重合?
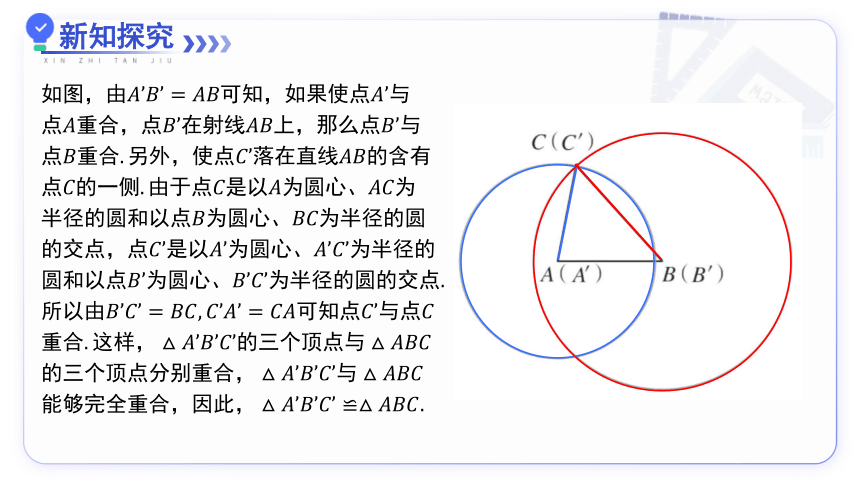
新知探究
XIN ZHI TAN JIU
新知探究
XIN ZHI TAN JIU
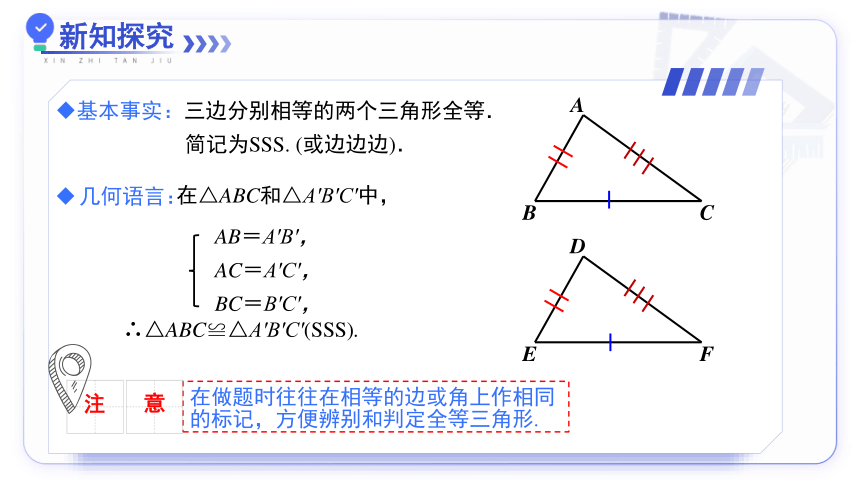
基本事实:三边分别相等的两个三角形全等.
简记为SSS. (或边边边).
在做题时往往在相等的边或角上作相同的标记,方便辨别和判定全等三角形.
注
意
A
B
C
D
E
F
几何语言:
AB=A′B′,
AC=A′C′,
BC=B′C′,
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′(SSS).
新知探究
XIN ZHI TAN JIU
在△ABC和△A′B′C′中,
∵
∴△ABC≌△A′B′C′ (SSS).
AB = A′B′,
AC = A′C′,
BC = B′C′,
第一个三角形的名称和对应的判定条件
第二个三角形的名称和对应的判定条件
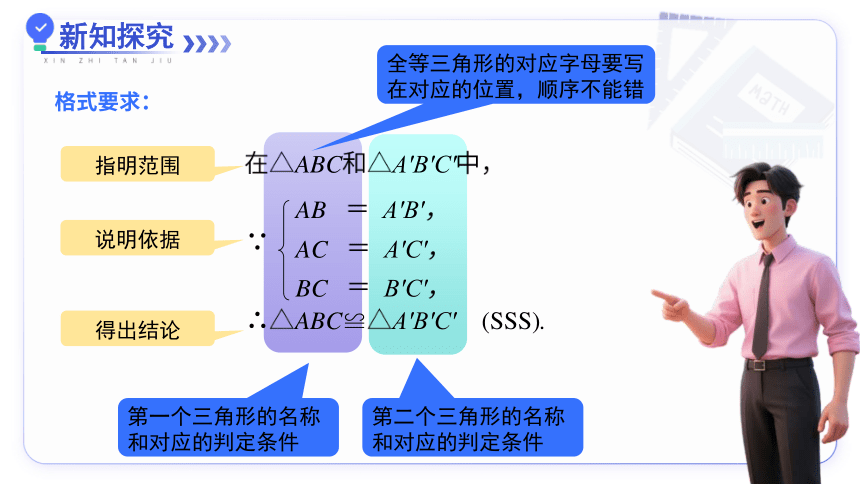
指明范围
说明依据
得出结论
全等三角形的对应字母要写在对应的位置,顺序不能错
格式要求:
典例精析
DIAN LI JING XI
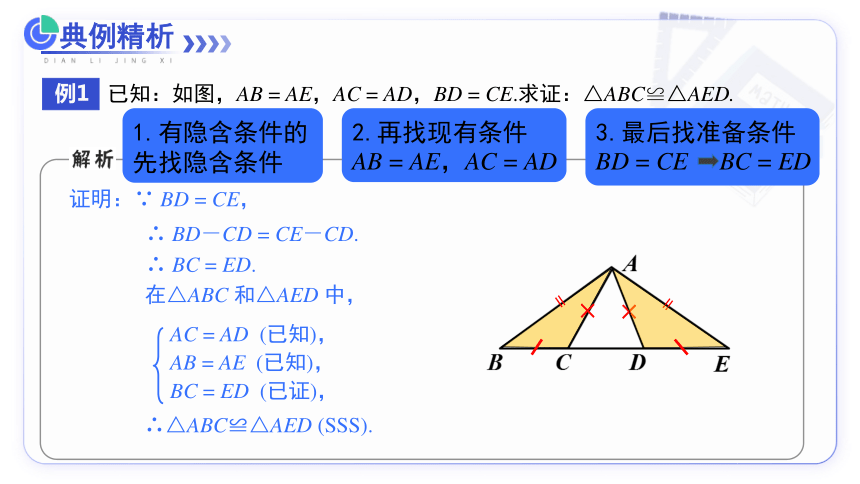
例1
已知:如图,AB = AE,AC = AD,BD = CE.求证:△ABC≌△AED.
证明:∵ BD = CE,
∴ BD-CD = CE-CD.
∴ BC = ED.
×
×
=
=
在△ABC 和△AED 中,
AC = AD (已知),
AB = AE (已知),
BC = ED (已证),
∴△ABC≌△AED (SSS).
1.有隐含条件的先找隐含条件
2.再找现有条件
AB = AE,AC = AD
3.最后找准备条件
BD = CE BC = ED
如何构造全等三角形?缺少的条件如何寻找?
典例精析
DIAN LI JING XI
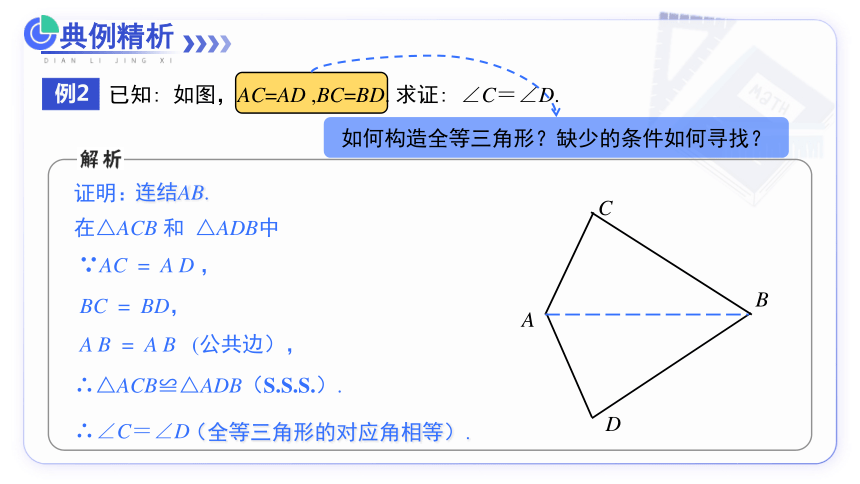
例2
已知: 如图,AC=AD ,BC=BD. 求证: ∠C=∠D.
A
B
C
D
证明:
在△ACB 和 △ADB中
∵AC = A D ,
BC = BD,
A B = A B (公共边),
∴△ACB≌△ADB(S.S.S.).
连结AB.
∴∠C=∠D
(全等三角形的对应角相等).
利用等式的性质进行转化
典例精析
DIAN LI JING XI
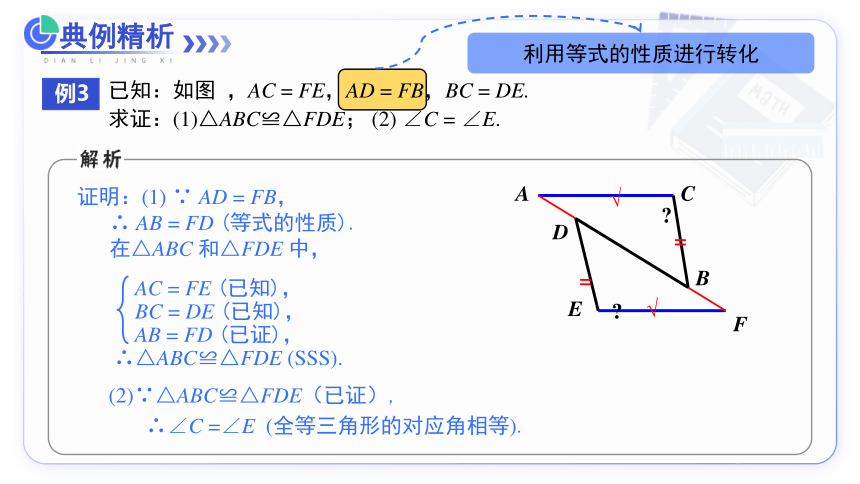
例3
AC = FE (已知),
BC = DE (已知),
AB = FD (已证),
∴△ABC≌△FDE (SSS).
已知:如图 ,AC = FE,AD = FB,BC = DE.
求证:(1)△ABC≌△FDE; (2) ∠C = ∠E.
证明:(1) ∵ AD = FB,
∴ AB = FD (等式的性质).
在△ABC 和△FDE 中,
A
C
E
D
B
F
=
=
√
√
(2)∵△ABC≌△FDE(已证),
∴∠C =∠E (全等三角形的对应角相等).
新知探究
XIN ZHI TAN JIU
思考
基本事实:三边分别相等的两个三角形全等.简记为SSS. (或边边边).
三角形的稳定性:只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做“三角形的稳定性”.
通过学习“边边边”判定三角形全等,你能解释三角形的稳定性吗?
利用以上事实,可以说明我们曾经做过的实验的结果:将三根木条钉成一个三角形木架,这个三角形木架的形状、大小就不变了,也就是三角形具有稳定性.
新知探究
XIN ZHI TAN JIU
思考
作法: (1) 作线段AB=c;
(2)分别以点 A,B为圆心,线段b,a为半径作弧,两弧相交于点 C;
(3)连接AC,BC,则△ABC就是所作的三角形 .
C
A
B
c
b
a
c
b
a
典例精析
DIAN LI JING XI
例4
分析:如果△ABD≌△ACD,那么∠ADB=∠ADC,从而有
△ABD与△ACD具备“边边边”的条件吗?
AB = AC (已知),
BD = CD (已知),
AD = AD (已证),
∴△ABD≌△ACD(SSS).
证明:(1) ∵ D是BC的中点,
∴BD =CD,
在△ABD和△ACDE中,
∴∠ADB=∠ADC,
又∵∠ADB+∠ADC=180°,
∴∠ADB=90°,
∴
新知探究
XIN ZHI TAN JIU
思考
已知一个三角形的三个内角分别为40°,60°和80°,请你画出这个三角形,并与同桌的进行比较,观察你们画出的三角形是否全等.
不一定全等
40°
80°
60°
40°
80°
60°
三角分别相等的两个三角形全等吗?
课堂小结
QING JING YIN RU
内容
应用
说明三角形的稳定性
已知三边,利用尺规作出三角形
边边边
有三边对应相等的两个三角形全等
(简写成“SSS”)
注意
说明两三角形全等所需的条件应按对应边的顺序书写
结论中所出现的边必须在所证明的两个三角形中
当堂练习
QING JING YIN RU
1.如图,E是AC上一点,AB=AD,BE=DE,可应用“SSS”证明三角形全等的是( )
A. △ABC≌△ADC B. △ABE≌△ADE
C. △CBE≌△CDE D. 以上选项都对
B
2. 如图,AB=CD,AD=BC,则下列结论:
①△ABC≌△CDB;②△ABC≌△CDA;
③△ABD ≌△CDB;④ BA∥DC.
正确的个数是 ( )
A. 1 B. 2 C. 3 D. 4
C
O
A
B
C
D
=
=
×
×
再找一组公共边即可
当堂练习
QING JING YIN RU
3.如图,△ABC中,AD=DE,AB=BE,∠A=100°,则∠DEC= 度.
80
4.如图,在△ABC 和△FED中,AC = FD,BC = ED,利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:
①AE=FB;②AB=FE;③AE=BE;④BF=BE,
可利用的是_______.
①②
△ABD≌△EBD吗?
当堂练习
QING JING YIN RU
5.如图,有一个三角形钢架,AB = AC,AD 是连接点 A 与 BC 中点 D 的支架.求证:
(1)△ABD≌△ACD;(2)∠BAD = ∠CAD.
C
B
D
A
证明:∵ D 是 BC 中点,
∴ BD = CD.
在△ABD 与△ACD 中,
∴△ABD≌△ACD (SSS).
AB = AC (已知),
BD = CD (已证),
AD = AD (公共边),
(2)由(1)得△ABD≌△ACD,
∴ ∠BAD = ∠CAD (全等三角形对应角相等).
检测下自己【例4】学会了吗!
当堂练习
QING JING YIN RU
6.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.
证明:∠A=∠D.
证明:∵BE=CF,∴BE+EC=CF+EC,
即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).∴∠A=∠D.
AB = DE (已知),
AC = DF (已知),
BC = EF (已证),
当堂练习
QING JING YIN RU
7.如图, 在四边形ABCD中,AD = CB,AB = CD. 求证:∠B = ∠D.
证明:在△ABC和△CDA 中,
∴ △ABC≌△CDA(SSS).
∴ ∠B =∠D(全等三角形的对应角相等).
CB = AD (已知),
AB = CD (已知),
AC = CA (公共边),
提示:不要忽略了公共边!
当堂练习
QING JING YIN RU
8. 如图,AD=BC,AC=BD. 求证:∠C=∠D.
证明:连接 A、B 两点.
∴△ABD≌△BAC (SSS).
AD = BC,
BD = AC,
AB = BA,
在△ABD 和△BAC 中,
∴∠D =∠C.
A
D
B
O
C
提示:无法通过判定△ADO≌△BCO来证明,能够作辅助线寻找其他的全等三角形呢?
当堂练习
QING JING YIN RU
9. 已知:如图,点 B、E、C、F 在同一直线上,AB = DE,AC = DF,BE = CF.
求证:(1)△ABC≌△DEF;
(2)∠A =∠D.
∴△ABC≌△DEF (SSS).
在△ABC 和△DEF 中,
AB = DE,
AC = DF,
BC = EF,
证明:(1)∵ BE = CF,
即 BC = EF.
∴ BE + EC = CF + CE,
(2) ∵△ABC≌△DEF (已证),
∴∠A =∠D (全等三角形对应角相等).
人教版 八年级上册
14.2(第3课时)
第十四章 全等三角形
边边边
复习回顾
FU XI HUI GU
思考
基本事实:两边和它们的夹角分别相等的两个三角形全等,
简写成“边角边”或“SAS”.
前面我们学习过哪些判定三角形全等的方法?
基本事实:有两角和它们的夹边分别相等的两个三角形全等,
简写成“角边角”或“ASA”.
基本事实:两角和其中一角的对边分别相等的两个三角形全等,
简写成“角角边”或“AAS”.
前面我们研究了两个三角形的两边和一角分别相等的情况以及两角和一边分别相等的情况.接下来研究三边分别相等的情况.
新知探究
XIN ZHI TAN JIU
探究
你能否证明两个三角形能完全重合?
新知探究
XIN ZHI TAN JIU
新知探究
XIN ZHI TAN JIU
基本事实:三边分别相等的两个三角形全等.
简记为SSS. (或边边边).
在做题时往往在相等的边或角上作相同的标记,方便辨别和判定全等三角形.
注
意
A
B
C
D
E
F
几何语言:
AB=A′B′,
AC=A′C′,
BC=B′C′,
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′(SSS).
新知探究
XIN ZHI TAN JIU
在△ABC和△A′B′C′中,
∵
∴△ABC≌△A′B′C′ (SSS).
AB = A′B′,
AC = A′C′,
BC = B′C′,
第一个三角形的名称和对应的判定条件
第二个三角形的名称和对应的判定条件
指明范围
说明依据
得出结论
全等三角形的对应字母要写在对应的位置,顺序不能错
格式要求:
典例精析
DIAN LI JING XI
例1
已知:如图,AB = AE,AC = AD,BD = CE.求证:△ABC≌△AED.
证明:∵ BD = CE,
∴ BD-CD = CE-CD.
∴ BC = ED.
×
×
=
=
在△ABC 和△AED 中,
AC = AD (已知),
AB = AE (已知),
BC = ED (已证),
∴△ABC≌△AED (SSS).
1.有隐含条件的先找隐含条件
2.再找现有条件
AB = AE,AC = AD
3.最后找准备条件
BD = CE BC = ED
如何构造全等三角形?缺少的条件如何寻找?
典例精析
DIAN LI JING XI
例2
已知: 如图,AC=AD ,BC=BD. 求证: ∠C=∠D.
A
B
C
D
证明:
在△ACB 和 △ADB中
∵AC = A D ,
BC = BD,
A B = A B (公共边),
∴△ACB≌△ADB(S.S.S.).
连结AB.
∴∠C=∠D
(全等三角形的对应角相等).
利用等式的性质进行转化
典例精析
DIAN LI JING XI
例3
AC = FE (已知),
BC = DE (已知),
AB = FD (已证),
∴△ABC≌△FDE (SSS).
已知:如图 ,AC = FE,AD = FB,BC = DE.
求证:(1)△ABC≌△FDE; (2) ∠C = ∠E.
证明:(1) ∵ AD = FB,
∴ AB = FD (等式的性质).
在△ABC 和△FDE 中,
A
C
E
D
B
F
=
=
√
√
(2)∵△ABC≌△FDE(已证),
∴∠C =∠E (全等三角形的对应角相等).
新知探究
XIN ZHI TAN JIU
思考
基本事实:三边分别相等的两个三角形全等.简记为SSS. (或边边边).
三角形的稳定性:只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做“三角形的稳定性”.
通过学习“边边边”判定三角形全等,你能解释三角形的稳定性吗?
利用以上事实,可以说明我们曾经做过的实验的结果:将三根木条钉成一个三角形木架,这个三角形木架的形状、大小就不变了,也就是三角形具有稳定性.
新知探究
XIN ZHI TAN JIU
思考
作法: (1) 作线段AB=c;
(2)分别以点 A,B为圆心,线段b,a为半径作弧,两弧相交于点 C;
(3)连接AC,BC,则△ABC就是所作的三角形 .
C
A
B
c
b
a
c
b
a
典例精析
DIAN LI JING XI
例4
分析:如果△ABD≌△ACD,那么∠ADB=∠ADC,从而有
△ABD与△ACD具备“边边边”的条件吗?
AB = AC (已知),
BD = CD (已知),
AD = AD (已证),
∴△ABD≌△ACD(SSS).
证明:(1) ∵ D是BC的中点,
∴BD =CD,
在△ABD和△ACDE中,
∴∠ADB=∠ADC,
又∵∠ADB+∠ADC=180°,
∴∠ADB=90°,
∴
新知探究
XIN ZHI TAN JIU
思考
已知一个三角形的三个内角分别为40°,60°和80°,请你画出这个三角形,并与同桌的进行比较,观察你们画出的三角形是否全等.
不一定全等
40°
80°
60°
40°
80°
60°
三角分别相等的两个三角形全等吗?
课堂小结
QING JING YIN RU
内容
应用
说明三角形的稳定性
已知三边,利用尺规作出三角形
边边边
有三边对应相等的两个三角形全等
(简写成“SSS”)
注意
说明两三角形全等所需的条件应按对应边的顺序书写
结论中所出现的边必须在所证明的两个三角形中
当堂练习
QING JING YIN RU
1.如图,E是AC上一点,AB=AD,BE=DE,可应用“SSS”证明三角形全等的是( )
A. △ABC≌△ADC B. △ABE≌△ADE
C. △CBE≌△CDE D. 以上选项都对
B
2. 如图,AB=CD,AD=BC,则下列结论:
①△ABC≌△CDB;②△ABC≌△CDA;
③△ABD ≌△CDB;④ BA∥DC.
正确的个数是 ( )
A. 1 B. 2 C. 3 D. 4
C
O
A
B
C
D
=
=
×
×
再找一组公共边即可
当堂练习
QING JING YIN RU
3.如图,△ABC中,AD=DE,AB=BE,∠A=100°,则∠DEC= 度.
80
4.如图,在△ABC 和△FED中,AC = FD,BC = ED,利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:
①AE=FB;②AB=FE;③AE=BE;④BF=BE,
可利用的是_______.
①②
△ABD≌△EBD吗?
当堂练习
QING JING YIN RU
5.如图,有一个三角形钢架,AB = AC,AD 是连接点 A 与 BC 中点 D 的支架.求证:
(1)△ABD≌△ACD;(2)∠BAD = ∠CAD.
C
B
D
A
证明:∵ D 是 BC 中点,
∴ BD = CD.
在△ABD 与△ACD 中,
∴△ABD≌△ACD (SSS).
AB = AC (已知),
BD = CD (已证),
AD = AD (公共边),
(2)由(1)得△ABD≌△ACD,
∴ ∠BAD = ∠CAD (全等三角形对应角相等).
检测下自己【例4】学会了吗!
当堂练习
QING JING YIN RU
6.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.
证明:∠A=∠D.
证明:∵BE=CF,∴BE+EC=CF+EC,
即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).∴∠A=∠D.
AB = DE (已知),
AC = DF (已知),
BC = EF (已证),
当堂练习
QING JING YIN RU
7.如图, 在四边形ABCD中,AD = CB,AB = CD. 求证:∠B = ∠D.
证明:在△ABC和△CDA 中,
∴ △ABC≌△CDA(SSS).
∴ ∠B =∠D(全等三角形的对应角相等).
CB = AD (已知),
AB = CD (已知),
AC = CA (公共边),
提示:不要忽略了公共边!
当堂练习
QING JING YIN RU
8. 如图,AD=BC,AC=BD. 求证:∠C=∠D.
证明:连接 A、B 两点.
∴△ABD≌△BAC (SSS).
AD = BC,
BD = AC,
AB = BA,
在△ABD 和△BAC 中,
∴∠D =∠C.
A
D
B
O
C
提示:无法通过判定△ADO≌△BCO来证明,能够作辅助线寻找其他的全等三角形呢?
当堂练习
QING JING YIN RU
9. 已知:如图,点 B、E、C、F 在同一直线上,AB = DE,AC = DF,BE = CF.
求证:(1)△ABC≌△DEF;
(2)∠A =∠D.
∴△ABC≌△DEF (SSS).
在△ABC 和△DEF 中,
AB = DE,
AC = DF,
BC = EF,
证明:(1)∵ BE = CF,
即 BC = EF.
∴ BE + EC = CF + CE,
(2) ∵△ABC≌△DEF (已证),
∴∠A =∠D (全等三角形对应角相等).
同课章节目录
