14.3(第1课时)角的平分线 课件(共26张PPT) 人教版(2024)数学八年级上册
文档属性
| 名称 | 14.3(第1课时)角的平分线 课件(共26张PPT) 人教版(2024)数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 30.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 16:25:11 | ||
图片预览






文档简介
(共26张PPT)
人教版 八年级上册
14.3(第1课时)
第十四章 全等三角形
角的平分线
复习回顾
FU XI HUI GU
什么是角的平分线?
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
O
A
B
C
如图,OC是∠AOB的平分线.
∠AOC=∠BOC= ∠AOB.
在纸上画一个角,怎么找到这个角的平分线?
可以用量角器、圆规、对折等方法.
实际生产应用中,又应该如何找到零件或者材料的角平分线呢?
思考
思考
思考
新知探究
XIN ZHI TAN JIU
思考
下图是一个平分角的仪器,其中AB =AD,BC =DC,将点A 放在角的顶点,AB 和AD 沿着角的两边放下,沿AC 画一条射线AE,AE 就是∠DAB 的平分线.你能说明它的道理吗?
A
B
D
C
E
理由如下:如图构成了△ADC和△ABC,
∵在△ADC和△ABC中,
AD=AB,
AC=AC,
DC=BC,
∴△ADC≌△ABC(SSS),
∴ ∠DAC=∠BAC.
∵点C在射线AE上,∴AE是这个角的平分线.
新知探究
XIN ZHI TAN JIU
思考
由上述结论,你能想到如何作一个角的平分线吗?
A
B
O
(1)已知什么?求作什么?
(2)把平分角的仪器放在角的两边,仪器的顶点与角的顶点重合,且仪器的两边相等,怎样在作图中体现这个过程呢
(3)在平分角的仪器中,BC = DC,怎样在作图中体现这个过程呢?
(4)你能说明为什么OC是∠AOB的平分线吗?
新知探究
XIN ZHI TAN JIU
探究
如图,已知:∠AOB.求作:∠AOB的平分线.
作法:
(1)以点O为圆心,适当长为半径画弧线,
交OA于点M,交OB于点N.
(2)分别以M、N为圆心,大于MN的长为
半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC,射线OC即为所求.
A
B
O
M
N
C
新知探究
XIN ZHI TAN JIU
思考
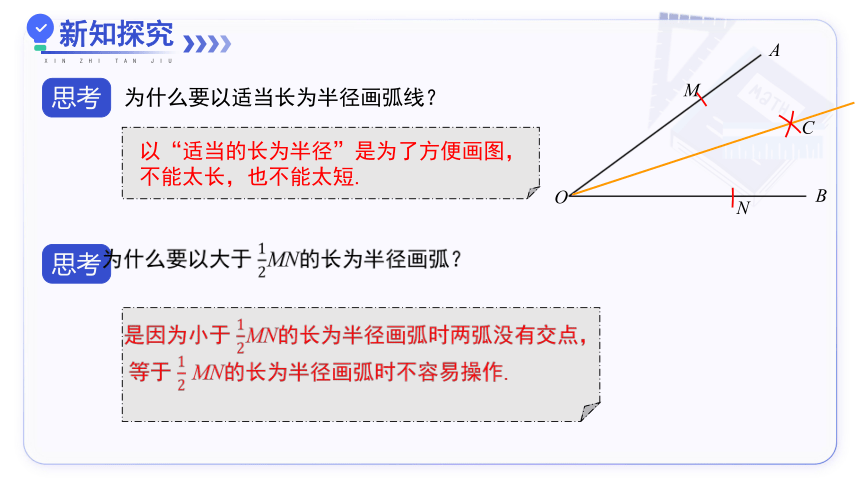
是因为小于 MN的长为半径画弧时两弧没有交点,
等于 MN的长为半径画弧时不容易操作.
为什么要以适当长为半径画弧线?
以“适当的长为半径”是为了方便画图,不能太长,也不能太短.
A
B
O
M
N
C
思考
为什么要以大于 MN的长为半径画弧?
新知探究
XIN ZHI TAN JIU
思考
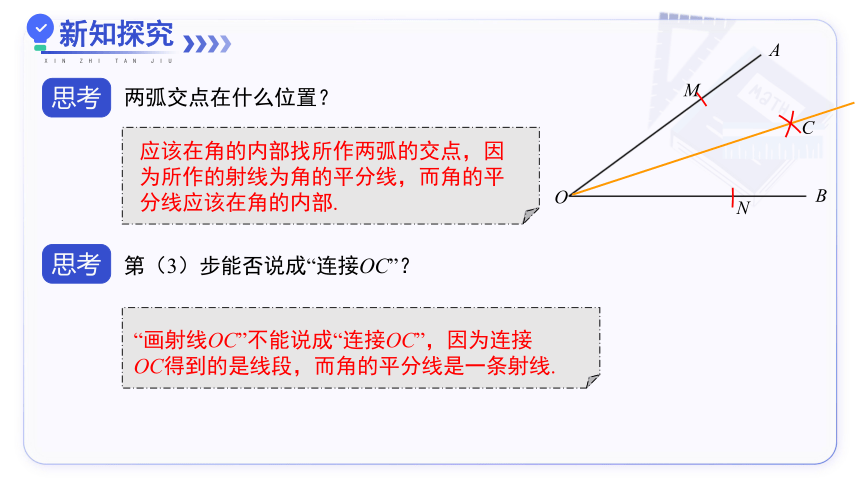
“画射线OC”不能说成“连接OC”,因为连接
OC得到的是线段,而角的平分线是一条射线.
两弧交点在什么位置?
应该在角的内部找所作两弧的交点,因为所作的射线为角的平分线,而角的平分线应该在角的内部.
A
B
O
M
N
C
思考
第(3)步能否说成“连接OC”?
新知探究
XIN ZHI TAN JIU
思考
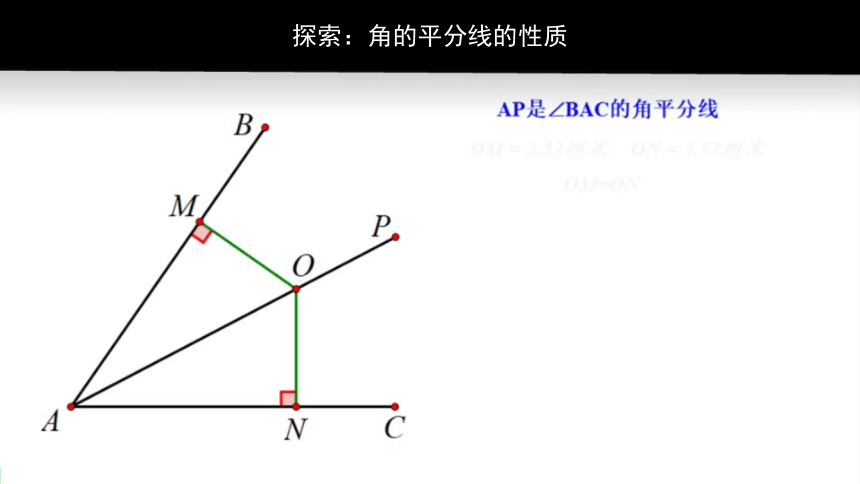
如图,任意作一个角∠AOB,作出∠AOB的平分线OC.在OC上任取一点P,过点P画出OA、OB的垂线,分别记垂足为D、E,测量PD、PE并作比较,你得到什么结论?在OC上再取几个点试一试.
根据以上测量,你能得到什么猜想?
次数 PD的长度 PE的长度
第1次
第2次
第3次
第n次
猜想:PD=PE
新知探究
XIN ZHI TAN JIU
思考
探索:角的平分线的性质
新知探究
XIN ZHI TAN JIU
思考
能否根据全等的知识来证明上述结论?
证明:
∵ PD⊥OA, PE⊥OB,
∴ ∠PDO =∠PEO = 90°.
在△PDO和△PEO中,
∠PDO =∠PEO,
∠DOP =∠EOP,
OP = OP,
∴ △PDO≌△PEO(AAS).
∴ PD = PE.
新知探究
XIN ZHI TAN JIU
角的平分线的性质
性质定理:角的平分线上的点到这个角的两边的距离相等.
应用所具备的条件:
(1) 点在角的平分线上;
(2) 到角两边的距离(垂直).
证明线段相等.
应用格式:
∵ OP 是∠AOB 的平分线,
∴ PD = PE.
PD⊥OA,PE⊥OB,
定理的作用:
新知探究
XIN ZHI TAN JIU
证明几何命题的一般步骤
(1)所画图形应符合题意,并具有一般性和代表性.在画图的时候要考虑是否存在不同的情形,若存在,则要分别画出图形,再分别进行证明;
(2)证明过程中的每一步推理都要有依据,比如:已知条件、定义、定理等.
(1)明确命题中的已知和求证;
(2)根据题意,画出图形,并用符号表示已知和求证;
(3)经过分析,找出由已知推出要证明的结论的途径,写出证明过程.
典例精析
DIAN LI JING XI
例1
①如图1,OC平分∠AOB,点P在OC上,D,E分别为OA,OB上的点,则PD=PE
②如图2,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E,则PD=PE
③如图3,OC平分∠AOB,点P在OC上,PD⊥OA,垂足分别为D.若PD=3,
则点P到OB的距离为3
O
B
A
C
P
D
图3
O
B
A
C
P
D
图2
E
O
B
A
C
P
D
图1
E
┐
┐
┐
判断下列命题是否正确:
(PD、PE不是角平分线上的点到角两边的距离).
(OC不是∠AOB的平分线).
(PD是∠AOB平分线OC上的点到OA的距离).
角的平分线的性质的标准条件
如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别为E、F.求证:EB=FC.
典例精析
DIAN LI JING XI
例2
证明:∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF.
∵在Rt△BDE和Rt△CDF中,
BD=CD,
DE=DF,
∴Rt△BDE≌Rt△CDF(HL).
∴EB=FC.
C
A
B
D
F
E
┐
┐
=DE+DB+EB=
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,
DE⊥AB,垂足为E,若AB=8cm,求△DEB的周长.
典例精析
DIAN LI JING XI
例3
解:在△ABC中,∠C=90°, ∴DC⊥AC.
又∵DE⊥AB,AD平分∠CAB, ∴DC=DE.
在Rt△ACD和Rt△AED中,
AD=AD,
DC=DE,
∴Rt△ACD≌Rt△AED(HL), ∴AC=AE.
∵AC=BC, ∴AE=BC, ∴△DEB的周长为8cm.
典例精析
DIAN LI JING XI
例4
如图,要在S 区建一个集贸市场,使它到 公路、铁路的距离相等,离两条公路交叉处500 m,请你帮忙设计一下,这个集贸市场应建于何处?
解:∵集贸市场到公路和铁路的距离相等
∴集贸市场应该在公路和铁路的角平分线上
不妨设公路和铁路的交点为O
作∠AOB的平分线OP
在OP上找一点S,使得OS=500m
点S即为集贸市场
A
B
O
P
看见距离,就想角的平分线!
回顾:三角形的三条角平分线交于一点如何证明?
典例精析
DIAN LI JING XI
例5
如图,△ABC的角平分线BM、CN相交于点P.
求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PE⊥BC于点E,作PD⊥AB于点D,
作PF⊥AC于点F,
∵BM、CN分别平分∠ABC、∠ACB
∴PD=PF
由于三角形三条角平分线交于一点
故点P也在∠A的平分线上
∴PD=PF=PE
∴点P到三边AB、BC、CA的距离相等
回顾三角形的三边关系.
典例精析
DIAN LI JING XI
例6
如图,在△ABC 的外角∠DAC 的平分线上任取一点P,PE⊥DB, PF⊥AC, 垂足分别为点E,F. 试探索BE + PF与PB的大小关系.
∴ PE=PF.
在△EBP中,BE+PE>PB,
∴ BE+PF>PB.
∵ AP是∠DAC的平分线,
又PE⊥DB, PF⊥AC,
解:
证明线段和差关系一般用截长补短
典例精析
DIAN LI JING XI
例7
如图,在△ABC 中,AD⊥DE,BE⊥DE,AC,BC 分别平分∠BAD,∠ABE,点C在线段DE上. 求证:AB=AD+BE.
M
证明:作CM⊥AB于点M.
∵ AC,BC 分别平分∠BAD,∠ABE,
∴ CD = CM,CE = CM.
在Rt△ACD和Rt△ACM中,
CM = CD,
AC = AC,
∴ Rt△ACD ≌Rt△ACM(HL).
∴ AD = AM. 同理, BE = BM.
又 AB=AM +BM, ∴ AB=AD +BE.
课堂小结
QING JING YIN RU
尺规作图
一个点:角平分线上的点
二距离:点到角两边的距离
两相等:两条垂线段(距离)相等
角的
平分线
基本要素
属于基本作图,必须熟练掌握
辅助线
过角平分线上一点向两边作垂线段
当堂练习
QING JING YIN RU
1.
B
A
M
当堂练习
QING JING YIN RU
4.直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.一处 B. 两处 C.三处 D.四处
D
A
M
当堂练习
QING JING YIN RU
32.5°
12
当堂练习
QING JING YIN RU
8. △ABC 中,∠C = 90°,AD 平分∠CAB,且 BC = 8,BD = 5,则点 D 到 AB 的距离是 .
A
B
C
D
3
E
7. 如图,DE⊥AB,DF⊥BG,垂足分别是 E,F,DE = DF,∠FDB = 60°,则∠EBF = °,BE = .
60
BF
E
B
D
F
A
C
G
当堂练习
QING JING YIN RU
9.如图,E 是∠AOB 的平分线上一点,EC⊥OA 于点C,ED⊥OB 于点D.
求证:(1)∠ECD=∠EDC; (2)OC=OD.
证明 (1)∵ 点E在∠BOA的平分线上,
EC⊥AO,ED⊥OB ,
∴ ED =EC.
∴ ∠ECD=∠EDC.
∴ △EDC 是个等腰三角形.
(2)在Rt△OED和Rt△OEC中,
OE= OE,
ED = EC,
∴ Rt△OED≌Rt△OEC(HL).
∴ OD=OC.
当堂练习
QING JING YIN RU
10.如图,在 Rt△ABC 中,AC=BC,∠C=90°,AP 平分∠BAC 交 BC 于点 P,若 PC=m,AB=14.
(1) 求△APB 的面积 (用含 m 的式子表示);
A
B
C
P
D
(2) 求△PDB 的周长.
∴ AB · PD = 7m.
解:由角平分线的性质,可知 PD = PC = m,
=
解:由题意可证 △ACP≌△ADP,
∴ AC = AD.
人教版 八年级上册
14.3(第1课时)
第十四章 全等三角形
角的平分线
复习回顾
FU XI HUI GU
什么是角的平分线?
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
O
A
B
C
如图,OC是∠AOB的平分线.
∠AOC=∠BOC= ∠AOB.
在纸上画一个角,怎么找到这个角的平分线?
可以用量角器、圆规、对折等方法.
实际生产应用中,又应该如何找到零件或者材料的角平分线呢?
思考
思考
思考
新知探究
XIN ZHI TAN JIU
思考
下图是一个平分角的仪器,其中AB =AD,BC =DC,将点A 放在角的顶点,AB 和AD 沿着角的两边放下,沿AC 画一条射线AE,AE 就是∠DAB 的平分线.你能说明它的道理吗?
A
B
D
C
E
理由如下:如图构成了△ADC和△ABC,
∵在△ADC和△ABC中,
AD=AB,
AC=AC,
DC=BC,
∴△ADC≌△ABC(SSS),
∴ ∠DAC=∠BAC.
∵点C在射线AE上,∴AE是这个角的平分线.
新知探究
XIN ZHI TAN JIU
思考
由上述结论,你能想到如何作一个角的平分线吗?
A
B
O
(1)已知什么?求作什么?
(2)把平分角的仪器放在角的两边,仪器的顶点与角的顶点重合,且仪器的两边相等,怎样在作图中体现这个过程呢
(3)在平分角的仪器中,BC = DC,怎样在作图中体现这个过程呢?
(4)你能说明为什么OC是∠AOB的平分线吗?
新知探究
XIN ZHI TAN JIU
探究
如图,已知:∠AOB.求作:∠AOB的平分线.
作法:
(1)以点O为圆心,适当长为半径画弧线,
交OA于点M,交OB于点N.
(2)分别以M、N为圆心,大于MN的长为
半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC,射线OC即为所求.
A
B
O
M
N
C
新知探究
XIN ZHI TAN JIU
思考
是因为小于 MN的长为半径画弧时两弧没有交点,
等于 MN的长为半径画弧时不容易操作.
为什么要以适当长为半径画弧线?
以“适当的长为半径”是为了方便画图,不能太长,也不能太短.
A
B
O
M
N
C
思考
为什么要以大于 MN的长为半径画弧?
新知探究
XIN ZHI TAN JIU
思考
“画射线OC”不能说成“连接OC”,因为连接
OC得到的是线段,而角的平分线是一条射线.
两弧交点在什么位置?
应该在角的内部找所作两弧的交点,因为所作的射线为角的平分线,而角的平分线应该在角的内部.
A
B
O
M
N
C
思考
第(3)步能否说成“连接OC”?
新知探究
XIN ZHI TAN JIU
思考
如图,任意作一个角∠AOB,作出∠AOB的平分线OC.在OC上任取一点P,过点P画出OA、OB的垂线,分别记垂足为D、E,测量PD、PE并作比较,你得到什么结论?在OC上再取几个点试一试.
根据以上测量,你能得到什么猜想?
次数 PD的长度 PE的长度
第1次
第2次
第3次
第n次
猜想:PD=PE
新知探究
XIN ZHI TAN JIU
思考
探索:角的平分线的性质
新知探究
XIN ZHI TAN JIU
思考
能否根据全等的知识来证明上述结论?
证明:
∵ PD⊥OA, PE⊥OB,
∴ ∠PDO =∠PEO = 90°.
在△PDO和△PEO中,
∠PDO =∠PEO,
∠DOP =∠EOP,
OP = OP,
∴ △PDO≌△PEO(AAS).
∴ PD = PE.
新知探究
XIN ZHI TAN JIU
角的平分线的性质
性质定理:角的平分线上的点到这个角的两边的距离相等.
应用所具备的条件:
(1) 点在角的平分线上;
(2) 到角两边的距离(垂直).
证明线段相等.
应用格式:
∵ OP 是∠AOB 的平分线,
∴ PD = PE.
PD⊥OA,PE⊥OB,
定理的作用:
新知探究
XIN ZHI TAN JIU
证明几何命题的一般步骤
(1)所画图形应符合题意,并具有一般性和代表性.在画图的时候要考虑是否存在不同的情形,若存在,则要分别画出图形,再分别进行证明;
(2)证明过程中的每一步推理都要有依据,比如:已知条件、定义、定理等.
(1)明确命题中的已知和求证;
(2)根据题意,画出图形,并用符号表示已知和求证;
(3)经过分析,找出由已知推出要证明的结论的途径,写出证明过程.
典例精析
DIAN LI JING XI
例1
①如图1,OC平分∠AOB,点P在OC上,D,E分别为OA,OB上的点,则PD=PE
②如图2,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E,则PD=PE
③如图3,OC平分∠AOB,点P在OC上,PD⊥OA,垂足分别为D.若PD=3,
则点P到OB的距离为3
O
B
A
C
P
D
图3
O
B
A
C
P
D
图2
E
O
B
A
C
P
D
图1
E
┐
┐
┐
判断下列命题是否正确:
(PD、PE不是角平分线上的点到角两边的距离).
(OC不是∠AOB的平分线).
(PD是∠AOB平分线OC上的点到OA的距离).
角的平分线的性质的标准条件
如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别为E、F.求证:EB=FC.
典例精析
DIAN LI JING XI
例2
证明:∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF.
∵在Rt△BDE和Rt△CDF中,
BD=CD,
DE=DF,
∴Rt△BDE≌Rt△CDF(HL).
∴EB=FC.
C
A
B
D
F
E
┐
┐
=DE+DB+EB=
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,
DE⊥AB,垂足为E,若AB=8cm,求△DEB的周长.
典例精析
DIAN LI JING XI
例3
解:在△ABC中,∠C=90°, ∴DC⊥AC.
又∵DE⊥AB,AD平分∠CAB, ∴DC=DE.
在Rt△ACD和Rt△AED中,
AD=AD,
DC=DE,
∴Rt△ACD≌Rt△AED(HL), ∴AC=AE.
∵AC=BC, ∴AE=BC, ∴△DEB的周长为8cm.
典例精析
DIAN LI JING XI
例4
如图,要在S 区建一个集贸市场,使它到 公路、铁路的距离相等,离两条公路交叉处500 m,请你帮忙设计一下,这个集贸市场应建于何处?
解:∵集贸市场到公路和铁路的距离相等
∴集贸市场应该在公路和铁路的角平分线上
不妨设公路和铁路的交点为O
作∠AOB的平分线OP
在OP上找一点S,使得OS=500m
点S即为集贸市场
A
B
O
P
看见距离,就想角的平分线!
回顾:三角形的三条角平分线交于一点如何证明?
典例精析
DIAN LI JING XI
例5
如图,△ABC的角平分线BM、CN相交于点P.
求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PE⊥BC于点E,作PD⊥AB于点D,
作PF⊥AC于点F,
∵BM、CN分别平分∠ABC、∠ACB
∴PD=PF
由于三角形三条角平分线交于一点
故点P也在∠A的平分线上
∴PD=PF=PE
∴点P到三边AB、BC、CA的距离相等
回顾三角形的三边关系.
典例精析
DIAN LI JING XI
例6
如图,在△ABC 的外角∠DAC 的平分线上任取一点P,PE⊥DB, PF⊥AC, 垂足分别为点E,F. 试探索BE + PF与PB的大小关系.
∴ PE=PF.
在△EBP中,BE+PE>PB,
∴ BE+PF>PB.
∵ AP是∠DAC的平分线,
又PE⊥DB, PF⊥AC,
解:
证明线段和差关系一般用截长补短
典例精析
DIAN LI JING XI
例7
如图,在△ABC 中,AD⊥DE,BE⊥DE,AC,BC 分别平分∠BAD,∠ABE,点C在线段DE上. 求证:AB=AD+BE.
M
证明:作CM⊥AB于点M.
∵ AC,BC 分别平分∠BAD,∠ABE,
∴ CD = CM,CE = CM.
在Rt△ACD和Rt△ACM中,
CM = CD,
AC = AC,
∴ Rt△ACD ≌Rt△ACM(HL).
∴ AD = AM. 同理, BE = BM.
又 AB=AM +BM, ∴ AB=AD +BE.
课堂小结
QING JING YIN RU
尺规作图
一个点:角平分线上的点
二距离:点到角两边的距离
两相等:两条垂线段(距离)相等
角的
平分线
基本要素
属于基本作图,必须熟练掌握
辅助线
过角平分线上一点向两边作垂线段
当堂练习
QING JING YIN RU
1.
B
A
M
当堂练习
QING JING YIN RU
4.直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.一处 B. 两处 C.三处 D.四处
D
A
M
当堂练习
QING JING YIN RU
32.5°
12
当堂练习
QING JING YIN RU
8. △ABC 中,∠C = 90°,AD 平分∠CAB,且 BC = 8,BD = 5,则点 D 到 AB 的距离是 .
A
B
C
D
3
E
7. 如图,DE⊥AB,DF⊥BG,垂足分别是 E,F,DE = DF,∠FDB = 60°,则∠EBF = °,BE = .
60
BF
E
B
D
F
A
C
G
当堂练习
QING JING YIN RU
9.如图,E 是∠AOB 的平分线上一点,EC⊥OA 于点C,ED⊥OB 于点D.
求证:(1)∠ECD=∠EDC; (2)OC=OD.
证明 (1)∵ 点E在∠BOA的平分线上,
EC⊥AO,ED⊥OB ,
∴ ED =EC.
∴ ∠ECD=∠EDC.
∴ △EDC 是个等腰三角形.
(2)在Rt△OED和Rt△OEC中,
OE= OE,
ED = EC,
∴ Rt△OED≌Rt△OEC(HL).
∴ OD=OC.
当堂练习
QING JING YIN RU
10.如图,在 Rt△ABC 中,AC=BC,∠C=90°,AP 平分∠BAC 交 BC 于点 P,若 PC=m,AB=14.
(1) 求△APB 的面积 (用含 m 的式子表示);
A
B
C
P
D
(2) 求△PDB 的周长.
∴ AB · PD = 7m.
解:由角平分线的性质,可知 PD = PC = m,
=
解:由题意可证 △ACP≌△ADP,
∴ AC = AD.
同课章节目录
