14.2三角形全等的判定(第1课时 边角边) 课件(共29张PPT) 人教版(2024)数学八年级上册
文档属性
| 名称 | 14.2三角形全等的判定(第1课时 边角边) 课件(共29张PPT) 人教版(2024)数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 33.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 16:26:18 | ||
图片预览




文档简介
(共29张PPT)
人教版 八年级上册
14.2(第1课时)
第十四章 全等三角形
边角边
情境引入
QING JING YIN RU
学校举行艺术节,为了装扮会场,需要一定数量的用纸折成的玫瑰花,这些玫瑰花是有一些相同的三角形纸片折叠而成,为了准备这些三角形纸片,老师应该提供哪些数据才能保证所有同学剪裁的三角形纸片全等呢?
思考
知识回顾
能够完全重合的两个三角形叫全等三角形.
全等三角形有什么性质:
全等三角形的对应边相等,对应角相等.
新知探究
XIN ZHI TAN JIU
探究
只给一个条件(一条边或一个角)画三角形时,大家画出的三角形
一定全等吗?
①只给一条边:
②只给一个角:
60°
60°
60°
不一定全等
不一定全等
新知探究
XIN ZHI TAN JIU
探究
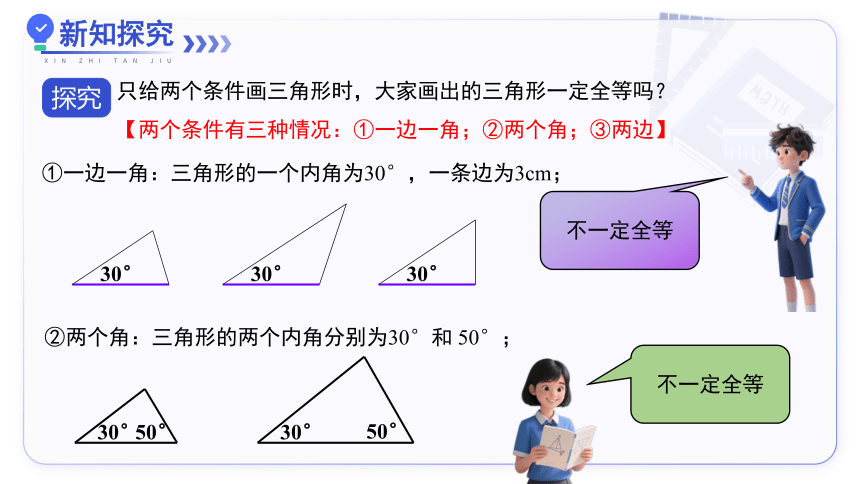
只给两个条件画三角形时,大家画出的三角形一定全等吗?
【两个条件有三种情况:①一边一角;②两个角;③两边】
①一边一角:三角形的一个内角为30°,一条边为3cm;
②两个角:三角形的两个内角分别为30°和 50°;
30°
30°
30°
30°
30°
50°
50°
不一定全等
不一定全等
新知探究
XIN ZHI TAN JIU
探究
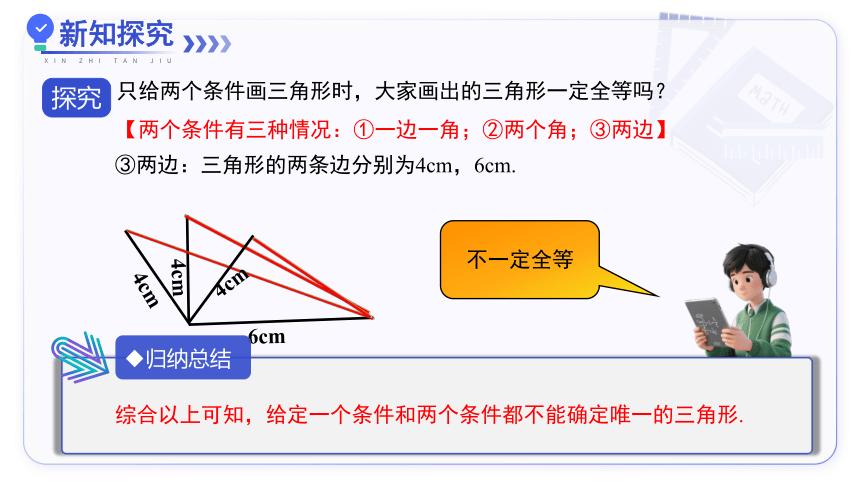
只给两个条件画三角形时,大家画出的三角形一定全等吗?
【两个条件有三种情况:①一边一角;②两个角;③两边】
③两边:三角形的两条边分别为4cm,6cm.
4cm
4cm
6cm
4cm
不一定全等
归纳总结
综合以上可知,给定一个条件和两个条件都不能确定唯一的三角形.
新知探究
XIN ZHI TAN JIU
思考
如果给出三个条件画三角形,你能说出有哪几种可能的情况吗?
有四种可能
(4)
三个角
(3)
三条边
(1)
两边一角
(2)
两角一边
新知探究
XIN ZHI TAN JIU
思考
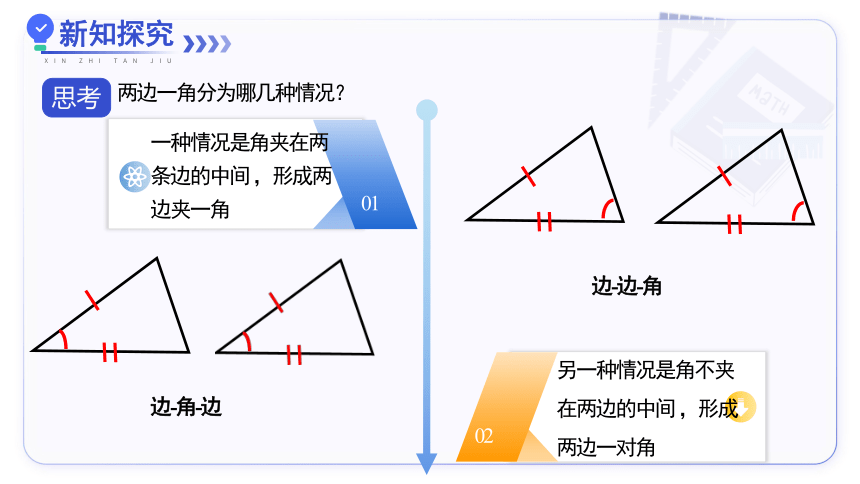
一种情况是角夹在两条边的中间 ,形成两边夹一角
01
02
另一种情况是角不夹在两边的中间 ,形成两边一对角
边-角-边
边-边-角
两边一角分为哪几种情况?
新知探究
XIN ZHI TAN JIU
思考
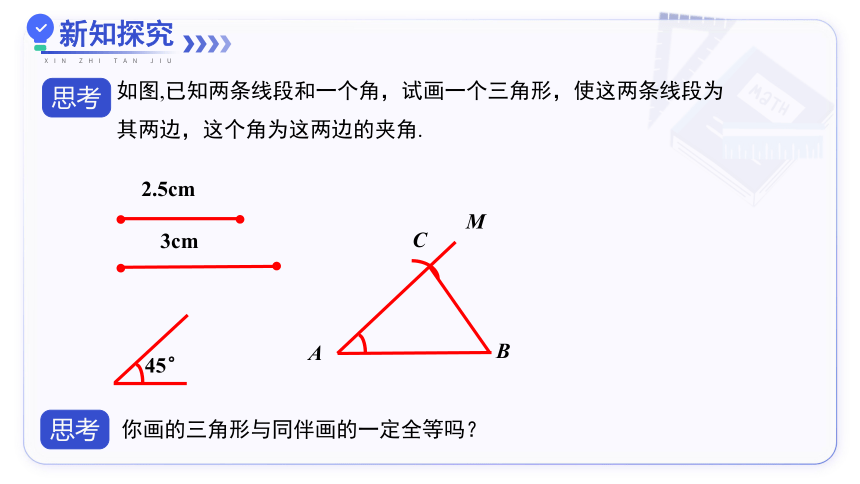
如图,已知两条线段和一个角,试画一个三角形,使这两条线段为其两边,这个角为这两边的夹角.
2.5cm
3cm
45°
A
B
C
M
你画的三角形与同伴画的一定全等吗?
思考
新知探究
XIN ZHI TAN JIU
几何语言:
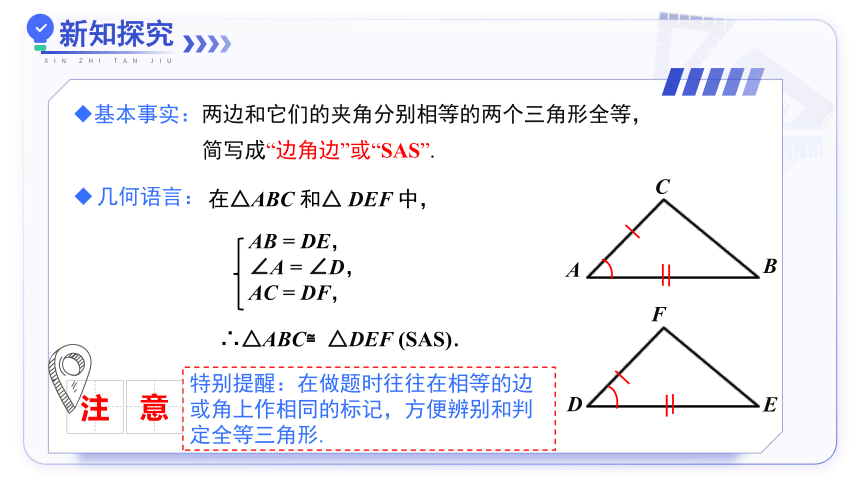
基本事实:两边和它们的夹角分别相等的两个三角形全等,
简写成“边角边”或“SAS”.
在△ABC 和△ DEF 中,
∴△ABC≌△DEF (SAS).
AB = DE,
∠A = ∠D,
AC = DF,
A
B
C
D
E
F
特别提醒:在做题时往往在相等的边或角上作相同的标记,方便辨别和判定全等三角形.
注
意
新知探究
XIN ZHI TAN JIU
格式要求:
第一个三角形的名称和对应的判定条件
第二个三角形的名称和对应的判定条件
指明范围
说明依据
得出结论
指出所用判定方法
全等三角形的对应字母要写在对应的位置,顺序不能错
在△ABC 和△ DEF 中,
∴△ABC ≌ △DEF (SAS).
AB = DE,
∠A = ∠D,
AC = DF,
三个条件必须按照
边
角
边
的顺序进行书写
(2025年湖北中考第17题)
典例精析
DIAN LI JING XI
例1
∠1=∠2,并在图中标出
在△ABD与△CBD中,
证明:
∴△ABC≌△ADC(SAS),
AB=AD (已知),
∠1=∠2 (已证),
AC=AC (公共边),
∴∠B=∠D.
∵AC平分∠BAD,
∴∠1=∠2.
已知:AD=AB,AC平分∠BAD ,证明:∠B=∠D.
1
2
AC既是△ABC的边,
又是△ADC的边.
我们称它为这两个三角形
的公共边.
典例精析
DIAN LI JING XI
例2
你能否找到隐藏条件?
如图,已知线段AC、BD相交于点E,AE=DE, BE=CE,
求证:△ABE≌△DCE.
证明:在△ABE和△DCE中,
AE=DE(已知),
∠AEB=∠DEC(对顶角相等),
BE=CE(已知),
∴△ABE≌△DCE (SAS)
典例精析
DIAN LI JING XI
例3
能否根据全等三角形的对应性质找到证明的条件?
证明:∵DE//AC,
∴∠EDB=∠A.
在△DEB与△ABC中,
DE=AB
∠EDB=∠A
BD=CA
∴△DEB≌△ABC(SAS).
如图,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D作DE//AC,并截取DE=AB,且点C,E在AB同侧,连结BE. 求证:△DEB≌△ABC.
新知探究
XIN ZHI TAN JIU
思考
根据之前讲解的作图步骤,请同学们作出以下三角形:两条边分别是2.5cm,3.5cm,长度为2.5cm的边所对的角为40°.
B
C
D
E
F
2.5cm
3.5cm
40°
40°
3.5cm
2.5cm
你画的三角形与同伴画的一定全等吗?为什么会出现这样的情况?
思考
新知探究
XIN ZHI TAN JIU
解释
A
C
B1
B2
归纳总结
两边分别相等且其中一组等边的对角也相等,两个三角形不一定全等.
注意观察角是否为两边的夹角!
典例精析
DIAN LI JING XI
例4
下列条件中,不能说明△ABC≌△DEF 的是 ( )
A. AB=DE,∠B=∠E,BC=EF
B. AB=DE,∠A=∠D,AC=DF
C. BC=EF,∠B=∠E,AC=DF
D. BC=EF,∠C=∠F,AC=DF
C
本题要判断能不能使△ABC≌△DEF,应看所给出的条件是不是两边和这两边的夹角,只有选项 C 的条件不符合,故选 C.
切记:SSA不能判定全等!
注
意
典例精析
DIAN LI JING XI
例5
如图,点E是正方形ABCD外一点,点F是线段AE上一点,AB=CB=CD=DA,∠ABC =∠BCD=∠CDA=∠DAB=90°,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.求证:△ABF≌△CBE.
证明:∵△EBF是等腰直角三角形,其中∠EBF=90°,∴BE=BF,∴∠ABC-∠CBF=∠EBF-∠CBF,
∴∠ABF=∠CBE,在△ABF和△CBE中,
AB=CB
∠ABF=∠CBE
BF=BE
∴△ABF≌△CBE(SAS).
手拉手模型
典例精析
DIAN LI JING XI
像这样两个顶角相等的等腰三角形共顶点时,所连接形成的两个三角形全等.
模型名称:手拉手模型
证明方法:SAS
模型和结论要牢记!
找齐证明全等的条件
典例精析
DIAN LI JING XI
例6
如图,在正方形ABCD中,AF=BE,AE 与DF 相交于点O.(1)试说明:△DAF≌△ABE;
利用全等三角形的性质求解!
如图,在正方形ABCD中,AF=BE,AE 与DF 相交于点O.(2)求∠AOD 的度数.
典例精析
DIAN LI JING XI
例6
十字架模型
典例精析
DIAN LI JING XI
像这样的模型叫做十字架模型,后面还会遇到它的变形.
典例精析
DIAN LI JING XI
例7
如图所示,在湖的两岸点A,B之间建一座观赏桥,由于条件限制,无法直接测量A,B两点之间的距离.请你用学过的数学知识按以下要求设计一个测量方案.
(1)画出测量示意图;
(2)写出测量步骤;
(3)计算点A,B之间的距离(写出求解或推理过程,结果用字母表示).
实际问题不能忽视,用数学的眼光观察,
要学会用数学的语言表达.
注
意
典例精析
DIAN LI JING XI
解:(1)如图所示:
(2)在湖岸上找到可以直接到达点A,B的一点O,
连结BO并延长到点C,使OC=OB;
连结AO并延长到点D,使OD=OA,
连结CD,则测量出CD的长度即为AB的长度.
(3)设CD=m.
在△COD 和△BOA中
OD=OA
∠COD=∠BOA
OC=OB
∴△COD ≌△BOA(S.A.S.),
∴CD=BA,即AB=m.
课堂小结
QING JING YIN RU
内容
注意
1. 已知两边,可以找“夹角”;
2. 已知一角和这角的一夹边,可找这角的另一夹边
边角边
应用
有两边及夹角对应相等的两个三角形
全等(简写成“SAS”)
为证明线段和角相等提供了新的证法
书写步骤:四步法(注意顺序!)
当堂练习
QING JING YIN RU
1.如图,a,b,c 分别是△ABC 的三边长,则下面与△ABC 一定全等的三角形是( )
B
2.如图,已知AB=AE,AC=AD,下列条件中能判定△ABC≌△AED 的是( )
A.BC=AE B.∠BAD=∠EAC
C.∠B=∠E D.∠C=∠D
B
能否利用三角形的内角和求出∠C?
找夹角!
当堂练习
QING JING YIN RU
B
C
SAS
当堂练习
QING JING YIN RU
5.如图,AC=BD,∠CAB= ∠DBA,求证:BC=AD.
A
B
C
D
证明:在△ABC与△BAD中,
AC=BD
∠CAB=∠DBA
AB=BA
∴△ABC≌△BAD(S.A.S.).
(已知),
(已知),
(公共边),
∴BC=AD
(全等三角形的对应边相等).
当堂练习
QING JING YIN RU
6.已知:如图,AB=DB,CB=EB,∠1=∠2,求证:∠A=∠D.
证明:∵ ∠1=∠2(已知),
∴∠1+∠DBC= ∠2+ ∠DBC(等式的性质),
即∠ABC=∠DBE.
在△ABC和△DBE中,
AB=DB(已知),
∠ABC=∠DBE(已证),
CB=EB(已知),
∴△ABC≌△DBE(S.A.S.).
∴ ∠A=∠D(全等三角形的对应角相等).
1
A
2
C
B
D
E
当堂练习
QING JING YIN RU
7.如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点.求证:AE=BD.
证明:∵△ABC和△ECD都是等腰直角三角形,
∴AC=BC,CE=CD,∠ECD=∠ACB=90°.
∴∠ECD-∠ACD=∠ACB-∠ACD,
即∠ACE=∠BCD.
在△ACE与△BCD中,
EC=DC,
∠ACE=∠BCD,
AC=BC,
∴△ACE≌△BCD (S.A.S.).
∴AE=BD.
人教版 八年级上册
14.2(第1课时)
第十四章 全等三角形
边角边
情境引入
QING JING YIN RU
学校举行艺术节,为了装扮会场,需要一定数量的用纸折成的玫瑰花,这些玫瑰花是有一些相同的三角形纸片折叠而成,为了准备这些三角形纸片,老师应该提供哪些数据才能保证所有同学剪裁的三角形纸片全等呢?
思考
知识回顾
能够完全重合的两个三角形叫全等三角形.
全等三角形有什么性质:
全等三角形的对应边相等,对应角相等.
新知探究
XIN ZHI TAN JIU
探究
只给一个条件(一条边或一个角)画三角形时,大家画出的三角形
一定全等吗?
①只给一条边:
②只给一个角:
60°
60°
60°
不一定全等
不一定全等
新知探究
XIN ZHI TAN JIU
探究
只给两个条件画三角形时,大家画出的三角形一定全等吗?
【两个条件有三种情况:①一边一角;②两个角;③两边】
①一边一角:三角形的一个内角为30°,一条边为3cm;
②两个角:三角形的两个内角分别为30°和 50°;
30°
30°
30°
30°
30°
50°
50°
不一定全等
不一定全等
新知探究
XIN ZHI TAN JIU
探究
只给两个条件画三角形时,大家画出的三角形一定全等吗?
【两个条件有三种情况:①一边一角;②两个角;③两边】
③两边:三角形的两条边分别为4cm,6cm.
4cm
4cm
6cm
4cm
不一定全等
归纳总结
综合以上可知,给定一个条件和两个条件都不能确定唯一的三角形.
新知探究
XIN ZHI TAN JIU
思考
如果给出三个条件画三角形,你能说出有哪几种可能的情况吗?
有四种可能
(4)
三个角
(3)
三条边
(1)
两边一角
(2)
两角一边
新知探究
XIN ZHI TAN JIU
思考
一种情况是角夹在两条边的中间 ,形成两边夹一角
01
02
另一种情况是角不夹在两边的中间 ,形成两边一对角
边-角-边
边-边-角
两边一角分为哪几种情况?
新知探究
XIN ZHI TAN JIU
思考
如图,已知两条线段和一个角,试画一个三角形,使这两条线段为其两边,这个角为这两边的夹角.
2.5cm
3cm
45°
A
B
C
M
你画的三角形与同伴画的一定全等吗?
思考
新知探究
XIN ZHI TAN JIU
几何语言:
基本事实:两边和它们的夹角分别相等的两个三角形全等,
简写成“边角边”或“SAS”.
在△ABC 和△ DEF 中,
∴△ABC≌△DEF (SAS).
AB = DE,
∠A = ∠D,
AC = DF,
A
B
C
D
E
F
特别提醒:在做题时往往在相等的边或角上作相同的标记,方便辨别和判定全等三角形.
注
意
新知探究
XIN ZHI TAN JIU
格式要求:
第一个三角形的名称和对应的判定条件
第二个三角形的名称和对应的判定条件
指明范围
说明依据
得出结论
指出所用判定方法
全等三角形的对应字母要写在对应的位置,顺序不能错
在△ABC 和△ DEF 中,
∴△ABC ≌ △DEF (SAS).
AB = DE,
∠A = ∠D,
AC = DF,
三个条件必须按照
边
角
边
的顺序进行书写
(2025年湖北中考第17题)
典例精析
DIAN LI JING XI
例1
∠1=∠2,并在图中标出
在△ABD与△CBD中,
证明:
∴△ABC≌△ADC(SAS),
AB=AD (已知),
∠1=∠2 (已证),
AC=AC (公共边),
∴∠B=∠D.
∵AC平分∠BAD,
∴∠1=∠2.
已知:AD=AB,AC平分∠BAD ,证明:∠B=∠D.
1
2
AC既是△ABC的边,
又是△ADC的边.
我们称它为这两个三角形
的公共边.
典例精析
DIAN LI JING XI
例2
你能否找到隐藏条件?
如图,已知线段AC、BD相交于点E,AE=DE, BE=CE,
求证:△ABE≌△DCE.
证明:在△ABE和△DCE中,
AE=DE(已知),
∠AEB=∠DEC(对顶角相等),
BE=CE(已知),
∴△ABE≌△DCE (SAS)
典例精析
DIAN LI JING XI
例3
能否根据全等三角形的对应性质找到证明的条件?
证明:∵DE//AC,
∴∠EDB=∠A.
在△DEB与△ABC中,
DE=AB
∠EDB=∠A
BD=CA
∴△DEB≌△ABC(SAS).
如图,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D作DE//AC,并截取DE=AB,且点C,E在AB同侧,连结BE. 求证:△DEB≌△ABC.
新知探究
XIN ZHI TAN JIU
思考
根据之前讲解的作图步骤,请同学们作出以下三角形:两条边分别是2.5cm,3.5cm,长度为2.5cm的边所对的角为40°.
B
C
D
E
F
2.5cm
3.5cm
40°
40°
3.5cm
2.5cm
你画的三角形与同伴画的一定全等吗?为什么会出现这样的情况?
思考
新知探究
XIN ZHI TAN JIU
解释
A
C
B1
B2
归纳总结
两边分别相等且其中一组等边的对角也相等,两个三角形不一定全等.
注意观察角是否为两边的夹角!
典例精析
DIAN LI JING XI
例4
下列条件中,不能说明△ABC≌△DEF 的是 ( )
A. AB=DE,∠B=∠E,BC=EF
B. AB=DE,∠A=∠D,AC=DF
C. BC=EF,∠B=∠E,AC=DF
D. BC=EF,∠C=∠F,AC=DF
C
本题要判断能不能使△ABC≌△DEF,应看所给出的条件是不是两边和这两边的夹角,只有选项 C 的条件不符合,故选 C.
切记:SSA不能判定全等!
注
意
典例精析
DIAN LI JING XI
例5
如图,点E是正方形ABCD外一点,点F是线段AE上一点,AB=CB=CD=DA,∠ABC =∠BCD=∠CDA=∠DAB=90°,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.求证:△ABF≌△CBE.
证明:∵△EBF是等腰直角三角形,其中∠EBF=90°,∴BE=BF,∴∠ABC-∠CBF=∠EBF-∠CBF,
∴∠ABF=∠CBE,在△ABF和△CBE中,
AB=CB
∠ABF=∠CBE
BF=BE
∴△ABF≌△CBE(SAS).
手拉手模型
典例精析
DIAN LI JING XI
像这样两个顶角相等的等腰三角形共顶点时,所连接形成的两个三角形全等.
模型名称:手拉手模型
证明方法:SAS
模型和结论要牢记!
找齐证明全等的条件
典例精析
DIAN LI JING XI
例6
如图,在正方形ABCD中,AF=BE,AE 与DF 相交于点O.(1)试说明:△DAF≌△ABE;
利用全等三角形的性质求解!
如图,在正方形ABCD中,AF=BE,AE 与DF 相交于点O.(2)求∠AOD 的度数.
典例精析
DIAN LI JING XI
例6
十字架模型
典例精析
DIAN LI JING XI
像这样的模型叫做十字架模型,后面还会遇到它的变形.
典例精析
DIAN LI JING XI
例7
如图所示,在湖的两岸点A,B之间建一座观赏桥,由于条件限制,无法直接测量A,B两点之间的距离.请你用学过的数学知识按以下要求设计一个测量方案.
(1)画出测量示意图;
(2)写出测量步骤;
(3)计算点A,B之间的距离(写出求解或推理过程,结果用字母表示).
实际问题不能忽视,用数学的眼光观察,
要学会用数学的语言表达.
注
意
典例精析
DIAN LI JING XI
解:(1)如图所示:
(2)在湖岸上找到可以直接到达点A,B的一点O,
连结BO并延长到点C,使OC=OB;
连结AO并延长到点D,使OD=OA,
连结CD,则测量出CD的长度即为AB的长度.
(3)设CD=m.
在△COD 和△BOA中
OD=OA
∠COD=∠BOA
OC=OB
∴△COD ≌△BOA(S.A.S.),
∴CD=BA,即AB=m.
课堂小结
QING JING YIN RU
内容
注意
1. 已知两边,可以找“夹角”;
2. 已知一角和这角的一夹边,可找这角的另一夹边
边角边
应用
有两边及夹角对应相等的两个三角形
全等(简写成“SAS”)
为证明线段和角相等提供了新的证法
书写步骤:四步法(注意顺序!)
当堂练习
QING JING YIN RU
1.如图,a,b,c 分别是△ABC 的三边长,则下面与△ABC 一定全等的三角形是( )
B
2.如图,已知AB=AE,AC=AD,下列条件中能判定△ABC≌△AED 的是( )
A.BC=AE B.∠BAD=∠EAC
C.∠B=∠E D.∠C=∠D
B
能否利用三角形的内角和求出∠C?
找夹角!
当堂练习
QING JING YIN RU
B
C
SAS
当堂练习
QING JING YIN RU
5.如图,AC=BD,∠CAB= ∠DBA,求证:BC=AD.
A
B
C
D
证明:在△ABC与△BAD中,
AC=BD
∠CAB=∠DBA
AB=BA
∴△ABC≌△BAD(S.A.S.).
(已知),
(已知),
(公共边),
∴BC=AD
(全等三角形的对应边相等).
当堂练习
QING JING YIN RU
6.已知:如图,AB=DB,CB=EB,∠1=∠2,求证:∠A=∠D.
证明:∵ ∠1=∠2(已知),
∴∠1+∠DBC= ∠2+ ∠DBC(等式的性质),
即∠ABC=∠DBE.
在△ABC和△DBE中,
AB=DB(已知),
∠ABC=∠DBE(已证),
CB=EB(已知),
∴△ABC≌△DBE(S.A.S.).
∴ ∠A=∠D(全等三角形的对应角相等).
1
A
2
C
B
D
E
当堂练习
QING JING YIN RU
7.如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点.求证:AE=BD.
证明:∵△ABC和△ECD都是等腰直角三角形,
∴AC=BC,CE=CD,∠ECD=∠ACB=90°.
∴∠ECD-∠ACD=∠ACB-∠ACD,
即∠ACE=∠BCD.
在△ACE与△BCD中,
EC=DC,
∠ACE=∠BCD,
AC=BC,
∴△ACE≌△BCD (S.A.S.).
∴AE=BD.
同课章节目录
