14.2三角形全等的判定(第2课时 角边角、角角边) 课件(共26张PPT) 人教版(2024)数学八年级上册
文档属性
| 名称 | 14.2三角形全等的判定(第2课时 角边角、角角边) 课件(共26张PPT) 人教版(2024)数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 34.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 16:26:59 | ||
图片预览


文档简介
(共26张PPT)
人教版 八年级上册
14.2(第2课时)
第十四章 全等三角形
角边角、角角边
复习回顾
FU XI HUI GU
几何语言:
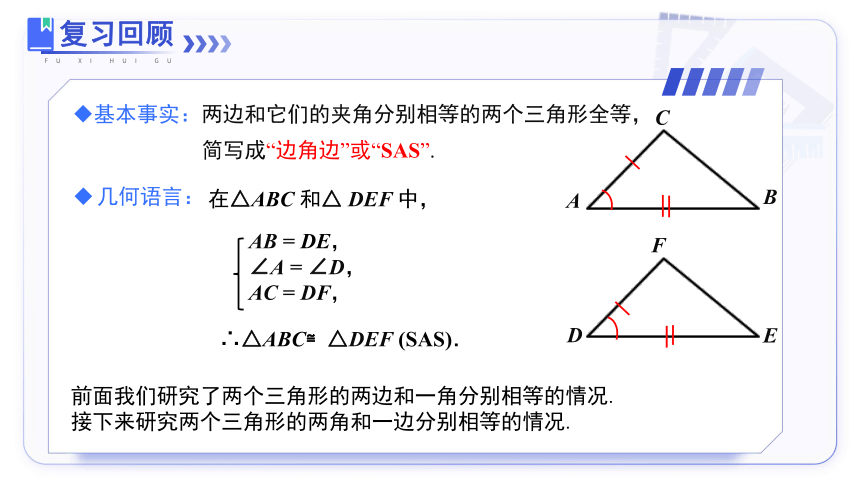
基本事实:两边和它们的夹角分别相等的两个三角形全等,
简写成“边角边”或“SAS”.
在△ABC 和△ DEF 中,
∴△ABC≌△DEF (SAS).
AB = DE,
∠A = ∠D,
AC = DF,
A
B
C
D
E
F
前面我们研究了两个三角形的两边和一角分别相等的情况.
接下来研究两个三角形的两角和一边分别相等的情况.
新知探究
XIN ZHI TAN JIU
思考
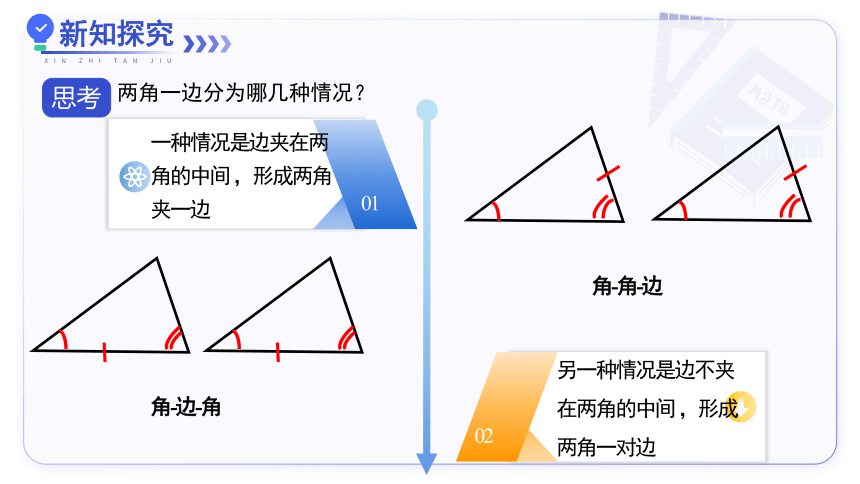
两角一边分为哪几种情况?
一种情况是边夹在两角的中间 ,形成两角夹一边
01
02
另一种情况是边不夹在两角的中间 ,形成两角一对边
角-边-角
角-角-边
新知探究
XIN ZHI TAN JIU
思考
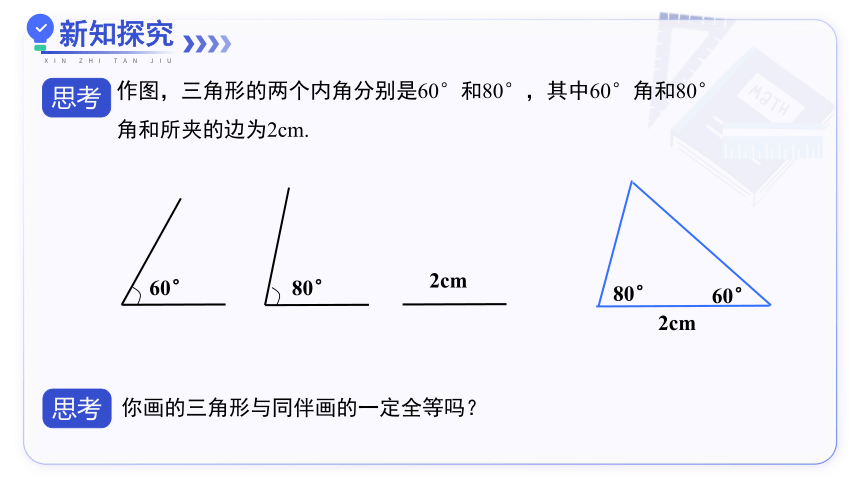
作图,三角形的两个内角分别是60°和80°,其中60°角和80°角和所夹的边为2cm.
2cm
80°
60°
2cm
80°
60°
你画的三角形与同伴画的一定全等吗?
思考
新知探究
XIN ZHI TAN JIU
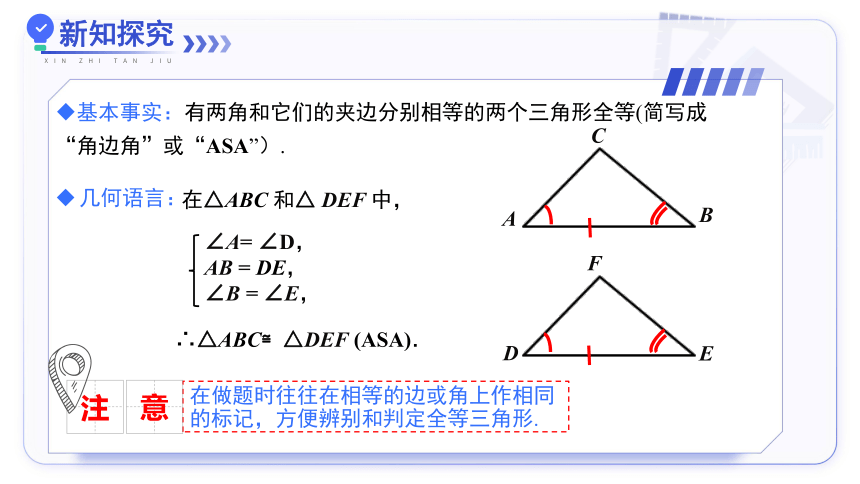
基本事实:有两角和它们的夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”).
几何语言:
在△ABC 和△ DEF 中,
∴△ABC≌△DEF (ASA).
∠A= ∠D,
AB = DE,
∠B = ∠E,
A
B
C
D
E
F
在做题时往往在相等的边或角上作相同的标记,方便辨别和判定全等三角形.
注
意
新知探究
XIN ZHI TAN JIU
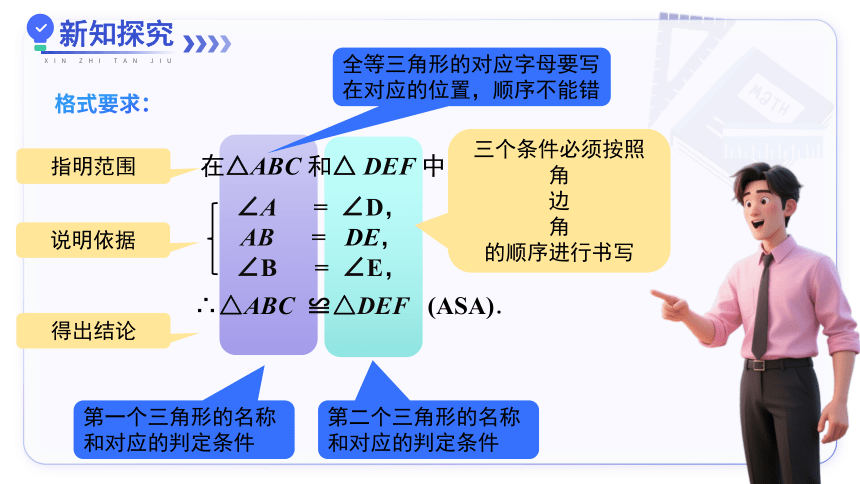
格式要求:
在△ABC 和△ DEF 中,
∴△ABC ≌△DEF (ASA).
∠A = ∠D,
AB = DE,
∠B = ∠E,
第一个三角形的名称和对应的判定条件
第二个三角形的名称和对应的判定条件
指明范围
说明依据
得出结论
全等三角形的对应字母要写在对应的位置,顺序不能错
三个条件必须按照
角
边
角
的顺序进行书写
典例精析
DIAN LI JING XI
例1
能得到什么结论帮助证明全等三角形?
是需要证明的全等三角形中的角吗?如何转化?
典例精析
DIAN LI JING XI
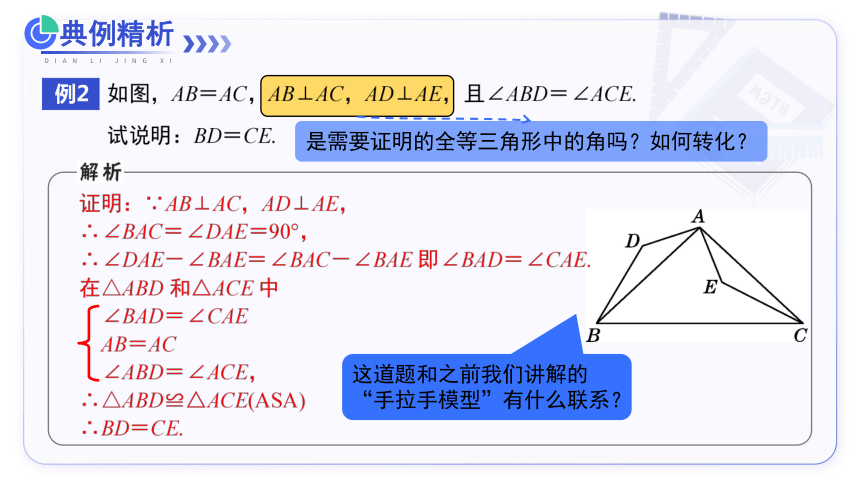
例2
这道题和之前我们讲解的“手拉手模型”有什么联系?
新知探究
XIN ZHI TAN JIU
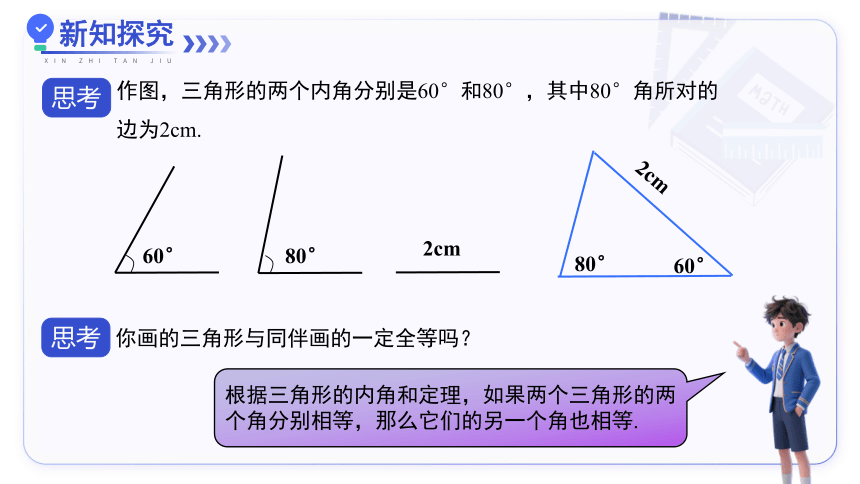
思考
作图,三角形的两个内角分别是60°和80°,其中80°角所对的边为2cm.
你画的三角形与同伴画的一定全等吗?
2cm
80°
60°
2cm
80°
60°
思考
根据三角形的内角和定理,如果两个三角形的两个角分别相等,那么它们的另一个角也相等.
新知探究
XIN ZHI TAN JIU
在做题时往往在相等的边或角上作相同的标记,方便辨别和判定全等三角形.
注
意
基本事实:两角和其中一角的对边分别相等的两个三角形全等.
简写成“角角边”或“AAS”.
在△ABC 和△ DEF 中,
∴△ABC≌△DEF (AAS).
∠A= ∠D,
∠B = ∠E,
BC=EF,
A
B
C
D
E
F
几何语言:
新知探究
XIN ZHI TAN JIU
在△ABC 和△ DEF 中,
∴△ABC ≌△DEF (AAS).
∠A = ∠D,
∠B = ∠E,
BC = EF,
第一个三角形的名称和对应的判定条件
第二个三角形的名称和对应的判定条件
指明范围
说明依据
得出结论
全等三角形的对应字母要写在对应的位置,顺序不能错
三个条件必须按照
角
角
边
的顺序进行书写
格式要求:
是全等三角形中的对应边吗?
典例精析
DIAN LI JING XI
例3
新知探究
XIN ZHI TAN JIU
思考
ASA“ASA”和'AAS”的区别与联系 “S”的意义 书写格式 联系
ASA “S”是两角的夹边 把夹边相等写在两角相等的中间 由三角形的内角和定理可知,“ASA”和“AAS”可以互相转化
AAS “S”是其中一角的对边 把两角相等写在一起,边相等放在最后 “ASA”和'AAS”两种判定全等的方法有何区别与联系?
能否找出和线段AM与BN相等的线段?
典例精析
DIAN LI JING XI
例4
(1)中的△ACM≌△CBN是否仍然成立?
典例精析
DIAN LI JING XI
例4
典例精析
DIAN LI JING XI
一线三(等)角模型(K字模型)
像这样,过等腰直角三角形直角顶点作直线l,过另外两个顶点作直线l的垂线,构成的两个三角形全等,这个模型称为“一线三(直)角(全等)模型”.
模型名称:(简称)一线三角模型
证明方法:AAS
模型及其变形和结论要牢记!
首先要明确用什么方法判定全等
如图,已知AD是∠BAC 的平分线,在不添加任何辅助线的前提下,要使
△AED ≌△AFD,可添加一个什么条件?并给予证明.
典例精析
DIAN LI JING XI
例5
解:(方法一) 添加AE=AF,证明如下:
∵AD是∠BAC的平分线, ∴∠EAD=∠FAD.
∵在△AED和△AFD中,
AE=AF,
∠EAD=∠FAD,
AD=AD,
∴△AED≌△AFD(SAS).
已有一边和一角分别相等,
可以构造一边相等选择“SAS”.
能添加角吗?
如图,已知AD是∠BAC 的平分线,在不添加任何辅助线的前提下,要使
△AED ≌△AFD,可添加一个什么条件?并给予证明.
典例精析
DIAN LI JING XI
例5
解:(方法二) 添加∠EDA=∠FDA ,证明如下:
∵AD是∠BAC的平分线, ∴∠EAD=∠FAD.
∵在△AED和△AFD中,
∠EDA=∠FDA,
AD=AD,
∠EAD=∠FAD,
∴△AED≌△AFD(ASA).
已有一边和一角分别相等,
可以构造一角相等选择“ASA”.
还能添加不同的角吗?
典例精析
DIAN LI JING XI
例5
解:(方法三)添加∠DEA=∠DFA,证明如下:
∵AD是∠BAC的平分线, ∴∠EAD=∠FAD.
∵在△AED和△AFD中,
∠DEA=∠DFA,
∠EAD=∠FAD,
AD=AD,
∴△AED≌△AFD(AAS).
如图,已知AD是∠BAC 的平分线,在不添加任何辅助线的前提下,要使
△AED ≌△AFD,可添加一个什么条件?并给予证明.
已有一边和一角分别相等,
可以构造一角相等选择“AAS”.
课堂小结
QING JING YIN RU
内容
两角及其夹边分别相等的两个三角形全等
(简写成 “ASA”)
两角和其中一个角的对边分别相等的两个三角形全等
(简写成 “AAS”)
角边角
角角边
应用
为证明线段和角相等提供了新的证法
注意
注意“角角边”、“角边角”中两角与边的区别
当堂练习
QING JING YIN RU
1.如图,∠1=∠2,∠3=∠4,OE=OF,
则图中全等的三角形有( )
A.1对 B.2对
C.3对 D.4对
B
2.如图,AB∥CD,且AB=CD,AC与BD相交于点E,则△ABE≌△CDE的根据是( )
A. 只能用ASA B. 只能用SSS
C. 只能用AAS D. 用ASA或AAS
A
B
D
C
E
D
△BFM≌△AEM
△BOE≌△AOF
当堂练习
QING JING YIN RU
3. 如图,已知∠ACB =∠DBC,∠ABC =∠CDB,判断下面的两个三角形是否全等,并说明理由.
答:不全等,因为 BC 虽然是公共边,但并不对应.
A
B
C
D
证明全等三角形一定要找到对应边和对应角,利用学过的判定方法来判定.
当堂练习
QING JING YIN RU
4.已知:∠ABC = ∠DCB,∠ACB = ∠DBC.
求证:△ABC≌△DCB.
∠ABC=∠DCB (已知),
BC=CB (公共边),
∠ACB=∠DBC (已知),
证明:
在△ABC 和△DCB 中,
∴△ABC≌△DCB (ASA ).
B
C
A
D
当堂练习
QING JING YIN RU
5.如图,点 D 在 AB 上,点 E 在 AC 上,AB = AC, ∠B =∠C,求证:AD = AE.
分析:证出△ACD≌△ABE,就可以得出 AD = AE.
证明:在△ACD 和△ABE 中,
∠A =∠A(公共角),
AC = AB(已知),
∠C =∠B (已知),
∴ △ACD≌△ABE(ASA).
∴ AD = AE.
A
B
C
D
E
当堂练习
QING JING YIN RU
6.如图,AB⊥BC,AD⊥DC,垂足分别为点B,点D,∠1=∠2.
求证:AB=AD.
A
B
C
D
1
2
证明:∵AB⊥BC,AD⊥DC, ∴∠ABC=∠ADC=90°.
∵在△ABC和△ADC中,∠1=∠2,∠ABC=∠ADC,
∴∠ACB=∠ACD.
在△ABC和△ADC中,
∠1=∠2,
AC=AC(公共边),
∠ACB=∠ACD,
∴△ABC≌△ADC(ASA), ∴AB=AD.
当堂练习
QING JING YIN RU
7.如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使得BC=CD.再画出BF的垂线DE,使得E与A,C在一条直线上,这时测得DE的长就是AB的长,为什么?
A
B
C
D
F
E
┐
┐
解:由题可知:AB⊥BC,ED⊥DC,
则∠ABC=∠EDC=90°.
在△ABC和△EDC中,
∠ABC=∠EDC,
BC=DC,
∠ACB=∠ECD,
∴△ABC≌△EDC(ASA).
∴AB=ED,则DE的长就是AB的长.
分析:只需证明 AB = DE.
人教版 八年级上册
14.2(第2课时)
第十四章 全等三角形
角边角、角角边
复习回顾
FU XI HUI GU
几何语言:
基本事实:两边和它们的夹角分别相等的两个三角形全等,
简写成“边角边”或“SAS”.
在△ABC 和△ DEF 中,
∴△ABC≌△DEF (SAS).
AB = DE,
∠A = ∠D,
AC = DF,
A
B
C
D
E
F
前面我们研究了两个三角形的两边和一角分别相等的情况.
接下来研究两个三角形的两角和一边分别相等的情况.
新知探究
XIN ZHI TAN JIU
思考
两角一边分为哪几种情况?
一种情况是边夹在两角的中间 ,形成两角夹一边
01
02
另一种情况是边不夹在两角的中间 ,形成两角一对边
角-边-角
角-角-边
新知探究
XIN ZHI TAN JIU
思考
作图,三角形的两个内角分别是60°和80°,其中60°角和80°角和所夹的边为2cm.
2cm
80°
60°
2cm
80°
60°
你画的三角形与同伴画的一定全等吗?
思考
新知探究
XIN ZHI TAN JIU
基本事实:有两角和它们的夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”).
几何语言:
在△ABC 和△ DEF 中,
∴△ABC≌△DEF (ASA).
∠A= ∠D,
AB = DE,
∠B = ∠E,
A
B
C
D
E
F
在做题时往往在相等的边或角上作相同的标记,方便辨别和判定全等三角形.
注
意
新知探究
XIN ZHI TAN JIU
格式要求:
在△ABC 和△ DEF 中,
∴△ABC ≌△DEF (ASA).
∠A = ∠D,
AB = DE,
∠B = ∠E,
第一个三角形的名称和对应的判定条件
第二个三角形的名称和对应的判定条件
指明范围
说明依据
得出结论
全等三角形的对应字母要写在对应的位置,顺序不能错
三个条件必须按照
角
边
角
的顺序进行书写
典例精析
DIAN LI JING XI
例1
能得到什么结论帮助证明全等三角形?
是需要证明的全等三角形中的角吗?如何转化?
典例精析
DIAN LI JING XI
例2
这道题和之前我们讲解的“手拉手模型”有什么联系?
新知探究
XIN ZHI TAN JIU
思考
作图,三角形的两个内角分别是60°和80°,其中80°角所对的边为2cm.
你画的三角形与同伴画的一定全等吗?
2cm
80°
60°
2cm
80°
60°
思考
根据三角形的内角和定理,如果两个三角形的两个角分别相等,那么它们的另一个角也相等.
新知探究
XIN ZHI TAN JIU
在做题时往往在相等的边或角上作相同的标记,方便辨别和判定全等三角形.
注
意
基本事实:两角和其中一角的对边分别相等的两个三角形全等.
简写成“角角边”或“AAS”.
在△ABC 和△ DEF 中,
∴△ABC≌△DEF (AAS).
∠A= ∠D,
∠B = ∠E,
BC=EF,
A
B
C
D
E
F
几何语言:
新知探究
XIN ZHI TAN JIU
在△ABC 和△ DEF 中,
∴△ABC ≌△DEF (AAS).
∠A = ∠D,
∠B = ∠E,
BC = EF,
第一个三角形的名称和对应的判定条件
第二个三角形的名称和对应的判定条件
指明范围
说明依据
得出结论
全等三角形的对应字母要写在对应的位置,顺序不能错
三个条件必须按照
角
角
边
的顺序进行书写
格式要求:
是全等三角形中的对应边吗?
典例精析
DIAN LI JING XI
例3
新知探究
XIN ZHI TAN JIU
思考
ASA“ASA”和'AAS”的区别与联系 “S”的意义 书写格式 联系
ASA “S”是两角的夹边 把夹边相等写在两角相等的中间 由三角形的内角和定理可知,“ASA”和“AAS”可以互相转化
AAS “S”是其中一角的对边 把两角相等写在一起,边相等放在最后 “ASA”和'AAS”两种判定全等的方法有何区别与联系?
能否找出和线段AM与BN相等的线段?
典例精析
DIAN LI JING XI
例4
(1)中的△ACM≌△CBN是否仍然成立?
典例精析
DIAN LI JING XI
例4
典例精析
DIAN LI JING XI
一线三(等)角模型(K字模型)
像这样,过等腰直角三角形直角顶点作直线l,过另外两个顶点作直线l的垂线,构成的两个三角形全等,这个模型称为“一线三(直)角(全等)模型”.
模型名称:(简称)一线三角模型
证明方法:AAS
模型及其变形和结论要牢记!
首先要明确用什么方法判定全等
如图,已知AD是∠BAC 的平分线,在不添加任何辅助线的前提下,要使
△AED ≌△AFD,可添加一个什么条件?并给予证明.
典例精析
DIAN LI JING XI
例5
解:(方法一) 添加AE=AF,证明如下:
∵AD是∠BAC的平分线, ∴∠EAD=∠FAD.
∵在△AED和△AFD中,
AE=AF,
∠EAD=∠FAD,
AD=AD,
∴△AED≌△AFD(SAS).
已有一边和一角分别相等,
可以构造一边相等选择“SAS”.
能添加角吗?
如图,已知AD是∠BAC 的平分线,在不添加任何辅助线的前提下,要使
△AED ≌△AFD,可添加一个什么条件?并给予证明.
典例精析
DIAN LI JING XI
例5
解:(方法二) 添加∠EDA=∠FDA ,证明如下:
∵AD是∠BAC的平分线, ∴∠EAD=∠FAD.
∵在△AED和△AFD中,
∠EDA=∠FDA,
AD=AD,
∠EAD=∠FAD,
∴△AED≌△AFD(ASA).
已有一边和一角分别相等,
可以构造一角相等选择“ASA”.
还能添加不同的角吗?
典例精析
DIAN LI JING XI
例5
解:(方法三)添加∠DEA=∠DFA,证明如下:
∵AD是∠BAC的平分线, ∴∠EAD=∠FAD.
∵在△AED和△AFD中,
∠DEA=∠DFA,
∠EAD=∠FAD,
AD=AD,
∴△AED≌△AFD(AAS).
如图,已知AD是∠BAC 的平分线,在不添加任何辅助线的前提下,要使
△AED ≌△AFD,可添加一个什么条件?并给予证明.
已有一边和一角分别相等,
可以构造一角相等选择“AAS”.
课堂小结
QING JING YIN RU
内容
两角及其夹边分别相等的两个三角形全等
(简写成 “ASA”)
两角和其中一个角的对边分别相等的两个三角形全等
(简写成 “AAS”)
角边角
角角边
应用
为证明线段和角相等提供了新的证法
注意
注意“角角边”、“角边角”中两角与边的区别
当堂练习
QING JING YIN RU
1.如图,∠1=∠2,∠3=∠4,OE=OF,
则图中全等的三角形有( )
A.1对 B.2对
C.3对 D.4对
B
2.如图,AB∥CD,且AB=CD,AC与BD相交于点E,则△ABE≌△CDE的根据是( )
A. 只能用ASA B. 只能用SSS
C. 只能用AAS D. 用ASA或AAS
A
B
D
C
E
D
△BFM≌△AEM
△BOE≌△AOF
当堂练习
QING JING YIN RU
3. 如图,已知∠ACB =∠DBC,∠ABC =∠CDB,判断下面的两个三角形是否全等,并说明理由.
答:不全等,因为 BC 虽然是公共边,但并不对应.
A
B
C
D
证明全等三角形一定要找到对应边和对应角,利用学过的判定方法来判定.
当堂练习
QING JING YIN RU
4.已知:∠ABC = ∠DCB,∠ACB = ∠DBC.
求证:△ABC≌△DCB.
∠ABC=∠DCB (已知),
BC=CB (公共边),
∠ACB=∠DBC (已知),
证明:
在△ABC 和△DCB 中,
∴△ABC≌△DCB (ASA ).
B
C
A
D
当堂练习
QING JING YIN RU
5.如图,点 D 在 AB 上,点 E 在 AC 上,AB = AC, ∠B =∠C,求证:AD = AE.
分析:证出△ACD≌△ABE,就可以得出 AD = AE.
证明:在△ACD 和△ABE 中,
∠A =∠A(公共角),
AC = AB(已知),
∠C =∠B (已知),
∴ △ACD≌△ABE(ASA).
∴ AD = AE.
A
B
C
D
E
当堂练习
QING JING YIN RU
6.如图,AB⊥BC,AD⊥DC,垂足分别为点B,点D,∠1=∠2.
求证:AB=AD.
A
B
C
D
1
2
证明:∵AB⊥BC,AD⊥DC, ∴∠ABC=∠ADC=90°.
∵在△ABC和△ADC中,∠1=∠2,∠ABC=∠ADC,
∴∠ACB=∠ACD.
在△ABC和△ADC中,
∠1=∠2,
AC=AC(公共边),
∠ACB=∠ACD,
∴△ABC≌△ADC(ASA), ∴AB=AD.
当堂练习
QING JING YIN RU
7.如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使得BC=CD.再画出BF的垂线DE,使得E与A,C在一条直线上,这时测得DE的长就是AB的长,为什么?
A
B
C
D
F
E
┐
┐
解:由题可知:AB⊥BC,ED⊥DC,
则∠ABC=∠EDC=90°.
在△ABC和△EDC中,
∠ABC=∠EDC,
BC=DC,
∠ACB=∠ECD,
∴△ABC≌△EDC(ASA).
∴AB=ED,则DE的长就是AB的长.
分析:只需证明 AB = DE.
同课章节目录
