1.1幂的乘方 课件(共25张PPT) 北师大版(2024)数学七年级下册
文档属性
| 名称 | 1.1幂的乘方 课件(共25张PPT) 北师大版(2024)数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 27.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 18:49:46 | ||
图片预览







文档简介
(共25张PPT)
幂的乘方
2025
年 级:七年级 学 科:数学(北师版)
目录
幂的乘方概念引入
01
幂的乘方运算规则
02
幂的乘方与同底数幂的乘法对比
03
幂的乘方的拓展应用
04
幂的乘方的常见误区与解决策略
05
幂的乘方的练习与巩固
06
幂的乘方概念引入
Part.
01
复习提问
am · an= (m,n 都是正整数)
am+n
新课引入
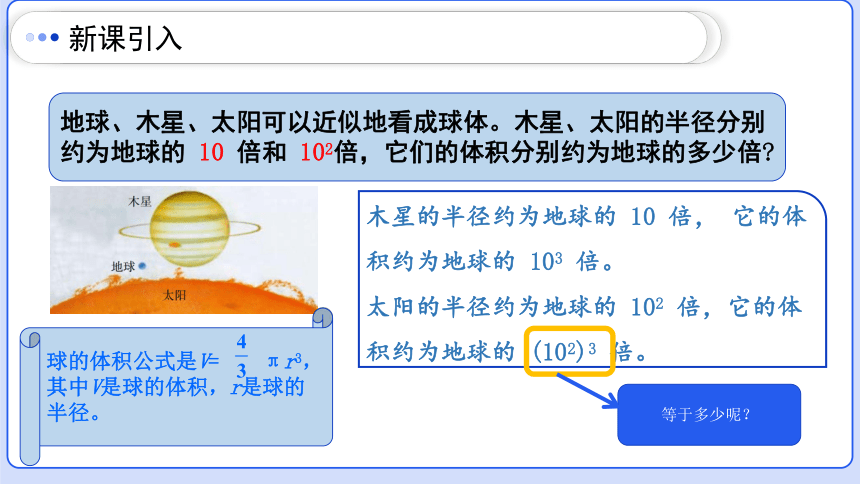
地球、木星、太阳可以近似地看成球体。木星、太阳的半径分别约为地球的 10 倍和 102倍,它们的体积分别约为地球的多少倍
球的体积公式是V= πr3,其中V是球的体积,r是球的半径。
木星的半径约为地球的 10 倍, 它的体积约为地球的 103 倍。
太阳的半径约为地球的 102 倍,它的体积约为地球的 (102)3 倍。
等于多少呢?
幂的乘方是指在一个幂的基础上再次进行乘方运算,即形如((am)n)的表达式。这里的(a)是底数,(m)是原指数,(n)是乘方后的指数。这种运算在数学中非常常见,尤其是在处理复杂计算和科学问题时,能够简化计算过程,提高计算效率。
幂的乘方的基本概念
幂的乘方的定义与意义
幂的乘方不仅在数学理论中占有重要地位,而且在实际生活中也有广泛的应用。例如,在计算复利、生物种群增长、放射性衰变等问题时,幂的乘方能够帮助我们快速准确地得到结果。通过学习幂的乘方,学生可以更好地理解数学与现实世界的联系,提高解决实际问题的能力。
幂的乘方的实际意义
幂的乘方的定义与意义
思考?
(1)(62)4
(2)(a2)3
(3)(am)2
(1)(62)4=62×62×62×62=62+2+2+2=62×4=68
(2)(a2)3=a2×a2×a2=a2+2+2=a2×3=a6
(3)(am)2=am×am=am+m=am×2=a2m
(am)n= (m,n都是正整数)
思考
(am)n = am · am· … · am · am
= am+m+…+m
= amn
n 个 am
n 个 m
(am)n= (m,n都是正整数)
(am)n=amn(m,n都是正整数)。
幂的乘方,底数 ,指数 。
不变
相乘
幂的乘方运算规则
Part.
02
幂的乘方的运算公式为((am)n = am n)。这个公式表明,当一个幂再次被乘方时,可以将原来的指数与新的指数相乘,得到最终的指数。这个规则是幂运算中的基本法则之一,掌握它对于解决复杂的数学问题至关重要。
01
幂的乘方的运算公式
幂的乘方的运算法则
为了更好地理解幂的乘方的运算规则,我们可以通过具体的例子来演示。例如,计算((23)2)时,根据运算公式,我们可以将指数3和2相乘,得到(23×2 = 26 = 64)。通过这样的例子,学生可以直观地看到幂的乘方运算的过程和结果,加深对这一规则的理解。
02
幂的乘方的运算示例
幂的乘方的运算法则
例题
(1)(72)4
(2)(c5)5
(3)(am)3
(4)-(x4)n
例题
解:(1)(72)4=72×4=78
(2)(c5)5=c5×5=c25
(3)(am)3=am 3=a3m
(4)-(x4)n=-x4 n=-x4n
幂的乘方与同底数幂的乘法对比
Part.
03
运算规则的不同
幂的乘方和同底数幂的乘法虽然都涉及幂的运算,但它们的运算规则有所不同。同底数幂的乘法是将指数相加,而幂的乘方是将指数相乘。例如,(am an = am+n),而((am)n = amn)。理解这两者的区别有助于学生在解决实际问题时正确应用相应的运算规则。
幂的乘方与同底数幂乘法的区别
应用场景的不同
幂的乘方和同底数幂的乘法在实际应用中也有不同的场景。同底数幂的乘法通常用于合并相同底数的幂,简化计算过程;而幂的乘方则用于处理多次乘方的情况,如计算复利或生物种群增长等。通过对比这两种运算,可以更好地理解它们在不同情境下的应用。
幂的乘方与同底数幂乘法的区别
例题
解:(y3)2 y=y3×2 y=y6 y=y7
(y3)2 y
幂的乘方的拓展应用
Part.
04
在物理学中,幂的乘方常用于描述各种自然现象和规律。例如,在计算物体的运动轨迹、能量转换或电磁场强度时,幂的乘方能够帮助我们快速准确地得到结果。通过学习幂的乘方,学生可以更好地理解物理现象背后的数学原理,提高解决物理问题的能力。
01
幂的乘方在物理中的应用
在化学中,幂的乘方同样发挥着重要作用。例如,在计算化学反应速率、溶液浓度或分子结构时,幂的乘方能够帮助我们简化计算过程,提高计算效率。通过将数学知识与化学知识相结合,学生可以更深入地理解化学反应的规律,为今后的学习和研究打下坚实的基础。
02
幂的乘方在化学中的应用
幂的乘方在科学计算中的应用
幂的乘方的常见误区与解决策略
Part.
05
在学习幂的乘方时,常常会混淆指数相加和相乘的规则。例如,有些学生可能会错误地认为((am)n = am+n),而不是正确的(amn)。
(a5)3≠a8
(a5)3=a15
指数相加与相乘的混淆
幂的乘方的常见误区
当底数为负数时,幂的乘方运算可能会出现错误。
例如,计算((- 2)3)2)时,学生可能会错误地得到(- 23 × 2 = - 26 = - 64),而正确的结果应该是((- 2)3 × 2 = (- 2)6 = 64)。
底数为负数时的运算错误
幂的乘方的常见误区
幂的乘方的练习与巩固
Part.
06
练一练
1.已知2x=6,4y=5,则2x+2y的值是 ( )
A.11 B.30 C.150 D.15
2.(-22)3=
3.(-x3)2 (-x2)3=
-26(或-64)
B
-x12
幂的乘方
2025
年 级:七年级 学 科:数学(北师版)
目录
幂的乘方概念引入
01
幂的乘方运算规则
02
幂的乘方与同底数幂的乘法对比
03
幂的乘方的拓展应用
04
幂的乘方的常见误区与解决策略
05
幂的乘方的练习与巩固
06
幂的乘方概念引入
Part.
01
复习提问
am · an= (m,n 都是正整数)
am+n
新课引入
地球、木星、太阳可以近似地看成球体。木星、太阳的半径分别约为地球的 10 倍和 102倍,它们的体积分别约为地球的多少倍
球的体积公式是V= πr3,其中V是球的体积,r是球的半径。
木星的半径约为地球的 10 倍, 它的体积约为地球的 103 倍。
太阳的半径约为地球的 102 倍,它的体积约为地球的 (102)3 倍。
等于多少呢?
幂的乘方是指在一个幂的基础上再次进行乘方运算,即形如((am)n)的表达式。这里的(a)是底数,(m)是原指数,(n)是乘方后的指数。这种运算在数学中非常常见,尤其是在处理复杂计算和科学问题时,能够简化计算过程,提高计算效率。
幂的乘方的基本概念
幂的乘方的定义与意义
幂的乘方不仅在数学理论中占有重要地位,而且在实际生活中也有广泛的应用。例如,在计算复利、生物种群增长、放射性衰变等问题时,幂的乘方能够帮助我们快速准确地得到结果。通过学习幂的乘方,学生可以更好地理解数学与现实世界的联系,提高解决实际问题的能力。
幂的乘方的实际意义
幂的乘方的定义与意义
思考?
(1)(62)4
(2)(a2)3
(3)(am)2
(1)(62)4=62×62×62×62=62+2+2+2=62×4=68
(2)(a2)3=a2×a2×a2=a2+2+2=a2×3=a6
(3)(am)2=am×am=am+m=am×2=a2m
(am)n= (m,n都是正整数)
思考
(am)n = am · am· … · am · am
= am+m+…+m
= amn
n 个 am
n 个 m
(am)n= (m,n都是正整数)
(am)n=amn(m,n都是正整数)。
幂的乘方,底数 ,指数 。
不变
相乘
幂的乘方运算规则
Part.
02
幂的乘方的运算公式为((am)n = am n)。这个公式表明,当一个幂再次被乘方时,可以将原来的指数与新的指数相乘,得到最终的指数。这个规则是幂运算中的基本法则之一,掌握它对于解决复杂的数学问题至关重要。
01
幂的乘方的运算公式
幂的乘方的运算法则
为了更好地理解幂的乘方的运算规则,我们可以通过具体的例子来演示。例如,计算((23)2)时,根据运算公式,我们可以将指数3和2相乘,得到(23×2 = 26 = 64)。通过这样的例子,学生可以直观地看到幂的乘方运算的过程和结果,加深对这一规则的理解。
02
幂的乘方的运算示例
幂的乘方的运算法则
例题
(1)(72)4
(2)(c5)5
(3)(am)3
(4)-(x4)n
例题
解:(1)(72)4=72×4=78
(2)(c5)5=c5×5=c25
(3)(am)3=am 3=a3m
(4)-(x4)n=-x4 n=-x4n
幂的乘方与同底数幂的乘法对比
Part.
03
运算规则的不同
幂的乘方和同底数幂的乘法虽然都涉及幂的运算,但它们的运算规则有所不同。同底数幂的乘法是将指数相加,而幂的乘方是将指数相乘。例如,(am an = am+n),而((am)n = amn)。理解这两者的区别有助于学生在解决实际问题时正确应用相应的运算规则。
幂的乘方与同底数幂乘法的区别
应用场景的不同
幂的乘方和同底数幂的乘法在实际应用中也有不同的场景。同底数幂的乘法通常用于合并相同底数的幂,简化计算过程;而幂的乘方则用于处理多次乘方的情况,如计算复利或生物种群增长等。通过对比这两种运算,可以更好地理解它们在不同情境下的应用。
幂的乘方与同底数幂乘法的区别
例题
解:(y3)2 y=y3×2 y=y6 y=y7
(y3)2 y
幂的乘方的拓展应用
Part.
04
在物理学中,幂的乘方常用于描述各种自然现象和规律。例如,在计算物体的运动轨迹、能量转换或电磁场强度时,幂的乘方能够帮助我们快速准确地得到结果。通过学习幂的乘方,学生可以更好地理解物理现象背后的数学原理,提高解决物理问题的能力。
01
幂的乘方在物理中的应用
在化学中,幂的乘方同样发挥着重要作用。例如,在计算化学反应速率、溶液浓度或分子结构时,幂的乘方能够帮助我们简化计算过程,提高计算效率。通过将数学知识与化学知识相结合,学生可以更深入地理解化学反应的规律,为今后的学习和研究打下坚实的基础。
02
幂的乘方在化学中的应用
幂的乘方在科学计算中的应用
幂的乘方的常见误区与解决策略
Part.
05
在学习幂的乘方时,常常会混淆指数相加和相乘的规则。例如,有些学生可能会错误地认为((am)n = am+n),而不是正确的(amn)。
(a5)3≠a8
(a5)3=a15
指数相加与相乘的混淆
幂的乘方的常见误区
当底数为负数时,幂的乘方运算可能会出现错误。
例如,计算((- 2)3)2)时,学生可能会错误地得到(- 23 × 2 = - 26 = - 64),而正确的结果应该是((- 2)3 × 2 = (- 2)6 = 64)。
底数为负数时的运算错误
幂的乘方的常见误区
幂的乘方的练习与巩固
Part.
06
练一练
1.已知2x=6,4y=5,则2x+2y的值是 ( )
A.11 B.30 C.150 D.15
2.(-22)3=
3.(-x3)2 (-x2)3=
-26(或-64)
B
-x12
同课章节目录
