23.4中位线(预习衔接.夯实基础.含解析)-2025-2026学年九年级上册数学华东师大版
文档属性
| 名称 | 23.4中位线(预习衔接.夯实基础.含解析)-2025-2026学年九年级上册数学华东师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 301.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 21:14:07 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
预习衔接.夯实基础 中位线
一.选择题(共5小题)
1.(2024秋 大连期中)如图,AD,CE都是△ABC的中线,连接ED,△ABC的面积是20cm2,则△CDE的面积是( )
A.2.5cm2 B.5cm2 C.7.5cm2 D.10cm2
2.(2024秋 南安市期中)为了倡导全民健身,某小区在公共活动区域安装了健身器材,其中跷跷板很受欢迎.如图,点O为跷跷板AB的中点,支柱OC垂直于地面,垂足为C,OC=0.6m.当跷跷板的一端A着地时,另一端B离地面的高度为( )
A.0.5m B.0.8m C.1m D.1.2m
3.(2024 兰州)如图,小张想估测被池塘隔开的A,B两处景观之间的距离,他先在AB外取一点C,然后步测出AC,BC的中点D,E,并步测出DE的长约为18m,由此估测A,B之间的距离约为( )
A.18m B.24m C.36m D.54m
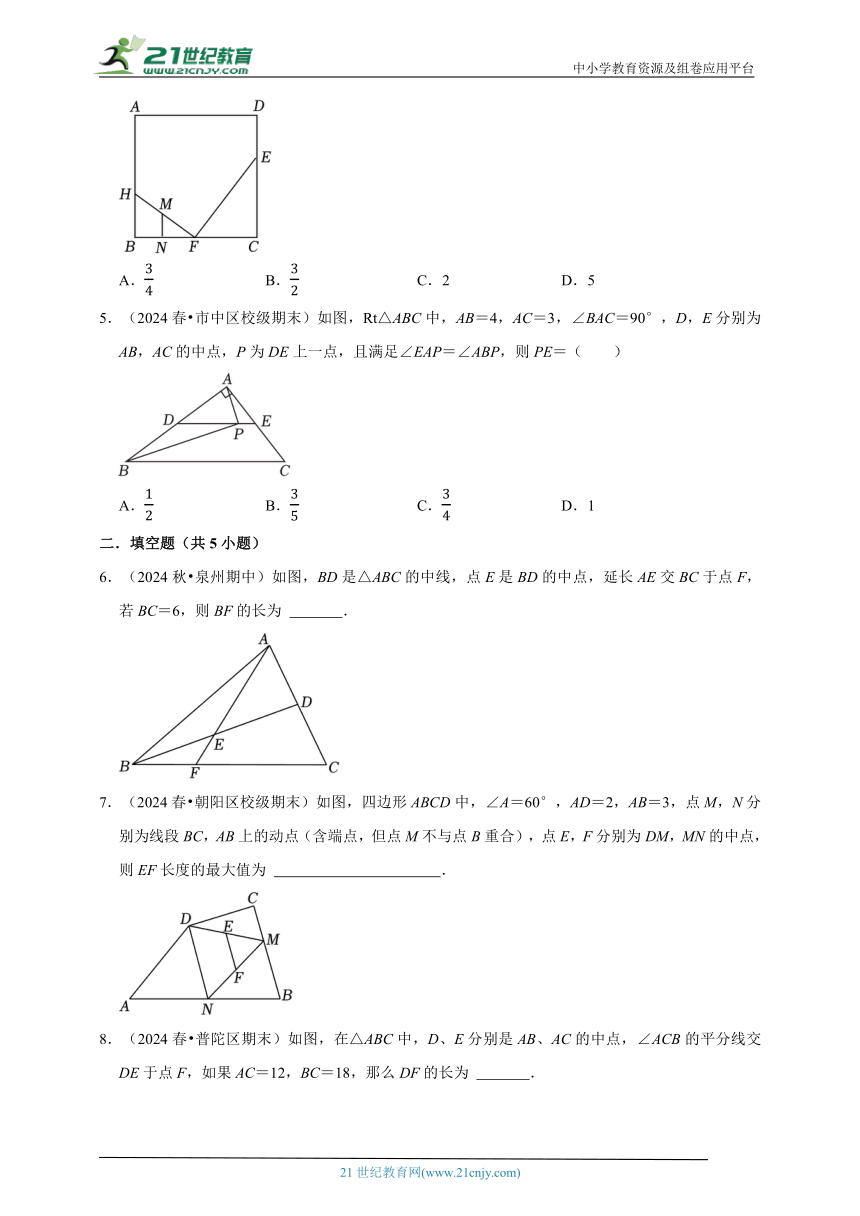
4.(2024秋 滕州市期中)如图所示,在边长为6的正方形ABCD中,E为CD上的点,F为BC的中点,过点F作HF⊥EF交AB于点H,点M,N分别是HF和BF的中点,若MN=1,则DE的长为( )
A. B. C.2 D.5
5.(2024春 市中区校级期末)如图,Rt△ABC中,AB=4,AC=3,∠BAC=90°,D,E分别为AB,AC的中点,P为DE上一点,且满足∠EAP=∠ABP,则PE=( )
A. B. C. D.1
二.填空题(共5小题)
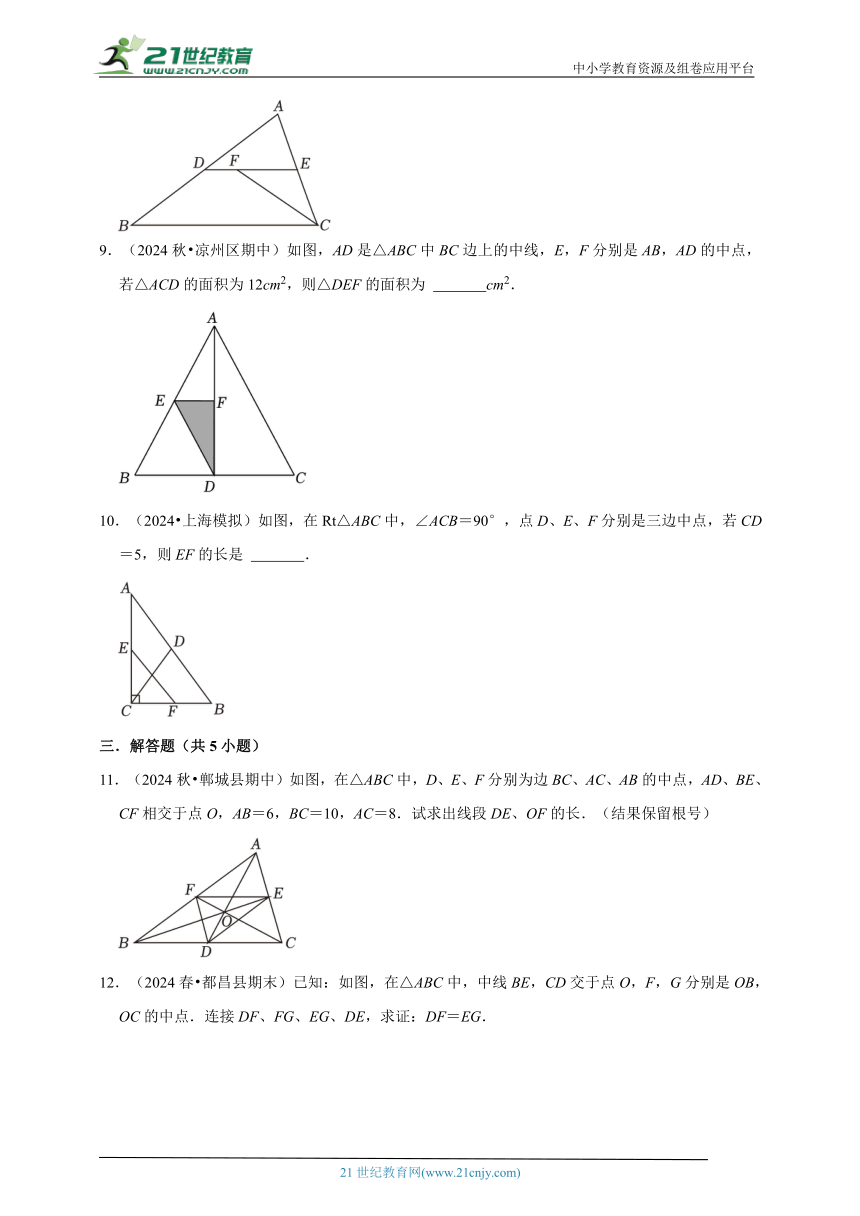
6.(2024秋 泉州期中)如图,BD是△ABC的中线,点E是BD的中点,延长AE交BC于点F,若BC=6,则BF的长为 .
7.(2024春 朝阳区校级期末)如图,四边形ABCD中,∠A=60°,AD=2,AB=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为 .
8.(2024春 普陀区期末)如图,在△ABC中,D、E分别是AB、AC的中点,∠ACB的平分线交DE于点F,如果AC=12,BC=18,那么DF的长为 .
9.(2024秋 凉州区期中)如图,AD是△ABC中BC边上的中线,E,F分别是AB,AD的中点,若△ACD的面积为12cm2,则△DEF的面积为 cm2.
10.(2024 上海模拟)如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别是三边中点,若CD=5,则EF的长是 .
三.解答题(共5小题)
11.(2024秋 郸城县期中)如图,在△ABC中,D、E、F分别为边BC、AC、AB的中点,AD、BE、CF相交于点O,AB=6,BC=10,AC=8.试求出线段DE、OF的长.(结果保留根号)
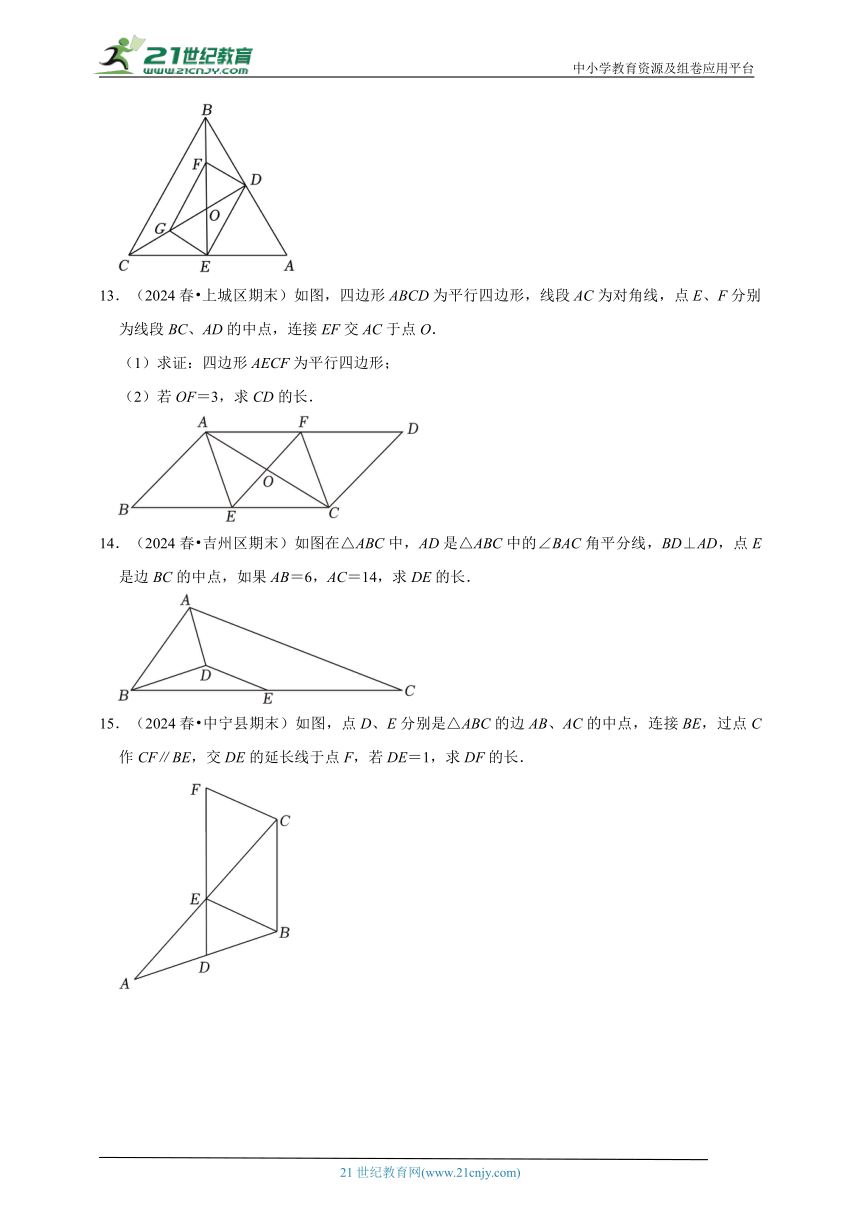
12.(2024春 都昌县期末)已知:如图,在△ABC中,中线BE,CD交于点O,F,G分别是OB,OC的中点.连接DF、FG、EG、DE,求证:DF=EG.
13.(2024春 上城区期末)如图,四边形ABCD为平行四边形,线段AC为对角线,点E、F分别为线段BC、AD的中点,连接EF交AC于点O.
(1)求证:四边形AECF为平行四边形;
(2)若OF=3,求CD的长.
14.(2024春 吉州区期末)如图在△ABC中,AD是△ABC中的∠BAC角平分线,BD⊥AD,点E是边BC的中点,如果AB=6,AC=14,求DE的长.
15.(2024春 中宁县期末)如图,点D、E分别是△ABC的边AB、AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若DE=1,求DF的长.
预习衔接.夯实基础 中位线
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 大连期中)如图,AD,CE都是△ABC的中线,连接ED,△ABC的面积是20cm2,则△CDE的面积是( )
A.2.5cm2 B.5cm2 C.7.5cm2 D.10cm2
【考点】三角形中位线定理;三角形的面积.
【专题】三角形;运算能力.
【答案】A
【分析】三角形的中线将三角形分成面积相等的两部分,三次利用该定理即可求得结果.
【解答】解:∵AD是△ABC的中线,
∴,
∵CE是△ABC的中线,
∴DE为△ABD的中线,
即,
∵DE为△BEC的中线,
∴S.
故选:A.
【点评】本题考查了利用三角形的中线求三角形的面积,掌握三角形中线的性质是解题的关键.
2.(2024秋 南安市期中)为了倡导全民健身,某小区在公共活动区域安装了健身器材,其中跷跷板很受欢迎.如图,点O为跷跷板AB的中点,支柱OC垂直于地面,垂足为C,OC=0.6m.当跷跷板的一端A着地时,另一端B离地面的高度为( )
A.0.5m B.0.8m C.1m D.1.2m
【考点】三角形中位线定理;相似三角形的判定与性质.
【专题】三角形;图形的相似.
【答案】D
【分析】过点B作BD垂直底面于点D,判断出OC是△ABD的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半可得BD=2OC.
【解答】解:如图,过点B作BD垂直底面于点D,
∵BD⊥AD,OC⊥AD,
∴BD∥OC,
∴△AOC∽△ABD,
∴,
∵点O为跷跷板AB的中点,
∴ACAD,
∴OC是△ABD的中位线,
∵OC=0.6m,
∴BD=2OC=1.2m,
故选:D.
【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,相似三角形的判定与性质,熟记定理是解题的关键.
3.(2024 兰州)如图,小张想估测被池塘隔开的A,B两处景观之间的距离,他先在AB外取一点C,然后步测出AC,BC的中点D,E,并步测出DE的长约为18m,由此估测A,B之间的距离约为( )
A.18m B.24m C.36m D.54m
【考点】三角形中位线定理.
【专题】三角形;推理能力.
【答案】C
【分析】依据题意,由D,E分别是边AC,BC的中点,首先判定DE是三角形的中位线,然后根据三角形的中位线定理求得AB的值即可
【解答】解:∵D、E分别是AC、BC的中点,
∴DE是△ABC的中位线.
∴根据三角形的中位线定理,得:AB=2DE=36m.
故选:C.
【点评】本题主要考查了三角形中位线定理的运用,解题时要能熟练掌握并能灵活运用三角形中位线定理是关键.
4.(2024秋 滕州市期中)如图所示,在边长为6的正方形ABCD中,E为CD上的点,F为BC的中点,过点F作HF⊥EF交AB于点H,点M,N分别是HF和BF的中点,若MN=1,则DE的长为( )
A. B. C.2 D.5
【考点】三角形中位线定理;正方形的性质;相似三角形的判定与性质.
【专题】三角形;矩形 菱形 正方形;图形的相似;推理能力.
【答案】B
【分析】根据三角形的中位线定理得HB=2MN=2,再由正方形的性质得由HF⊥EF,得∠HFE=90°,推导出∠BFH=∠CEF,进而证明△BFH∽△CEF,得,则CE=4.5,于是得到问题的答案.
【解答】解:∵点M,N分别是HF和BF的中点,
∴BN=FN,HM=FM,
∴MN是△HBF的中位线,
∵MN=1,
∴BH=2MN=2,
∵四边形ABCD是正方形,
∴BC=CD=6,∠B=∠C=90°,
∵F为BC的中点,
∴CF=BF=3,
∵HF⊥EF,
∴∠HFE=90°,
∴∠BFH=∠CEF,
∴△BFH∽△CEF,
∴,
∴,
∴CE=4.5,
∴,
故选:B.
【点评】此题重点考查正方形的性质,直角三角形的两个锐角互余、相似三角形的判定与性质、三角形的中位线定理等知识,证明△BFH∽△CEF是解题的关键.
5.(2024春 市中区校级期末)如图,Rt△ABC中,AB=4,AC=3,∠BAC=90°,D,E分别为AB,AC的中点,P为DE上一点,且满足∠EAP=∠ABP,则PE=( )
A. B. C. D.1
【考点】三角形中位线定理;全等三角形的判定与性质.
【专题】等腰三角形与直角三角形;推理能力.
【答案】A
【分析】根据直角三角形斜边上的中线的性质求出DP,根据勾股定理求出BC,根据三角形中位线定理求出DE,进而求出PE.
【解答】解:∵∠BAC=90°,
∴∠BAP+∠EAP=90°,
∵∠EAP=∠ABP,
∴∠ABP+∠EAP=90°,
∴∠APB=90°,
∵D为AB的中点,
∴DPAB=2,
在Rt△ABC中,AB=4,AC=3,
则BC5,
∵D,E分别为AB,AC的中点,
∴DE是△ABC的中位线,
∴DEBC,
∴PE=DE﹣DP,
故选:A.
【点评】本题考查的是三角形中位线定理,熟记三角形中位线等于第三边的一半是解题的关键.
二.填空题(共5小题)
6.(2024秋 泉州期中)如图,BD是△ABC的中线,点E是BD的中点,延长AE交BC于点F,若BC=6,则BF的长为 2 .
【考点】三角形中位线定理.
【专题】三角形;运算能力.
【答案】2.
【分析】取FC的中点H,连接DH,根据三角形中位线定理解答即可.
【解答】解:取FC的中点H,连接DH,
∵CD=DA,
∴DH是△ACF的中位线,
∴DH∥AF,
∵BE=ED,
∴EF是△BEF的中位线,
∴BF=FH,
∴,
故答案为:2.
【点评】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
7.(2024春 朝阳区校级期末)如图,四边形ABCD中,∠A=60°,AD=2,AB=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为 .
【考点】三角形中位线定理.
【专题】三角形;推理能力.
【答案】.
【分析】根据三角形的中位线定理得出 ,从而可知DN最大时,EF最大,因为N与B重合时DN最大,此时根据勾股定理求得DN,从而求得EF的最大值.连接DB,过点D作DH⊥AB 交AB于点H,再利用直角三角形的性质和勾股定理求解即可.
【解答】解:∵ED=EM,MF=FN,,
∴DN最大时,EF最大,
∴N与B重合时DN=DB最大,
在Rt△ADH中,
∵∠A=60°,
∴∠ADH=30°,
∴,,
∴BH=AB﹣AH=3﹣1=2,
∴,
∴.
故答案为:.
【点评】本题考查了三角形的中位线定理,勾股定理,含30度角的直角三角形的性质,利用三角形中位线求得是解题的关键.
8.(2024春 普陀区期末)如图,在△ABC中,D、E分别是AB、AC的中点,∠ACB的平分线交DE于点F,如果AC=12,BC=18,那么DF的长为 3 .
【考点】三角形中位线定理;角平分线的性质.
【专题】线段、角、相交线与平行线;三角形;运算能力;推理能力.
【答案】3.
【分析】根据三角形中位线定理得到DE∥BC,DEBC,求出EF,进而求出DF.
【解答】解:∵CF是∠ABC的平分线,
∴∠ACF=∠FCB,
∵点D、E分别为边AB、AC的中点,
∴DE∥BC,DEBC9,
∴∠EFC=∠FCB,
∴∠ACF=∠EFC,
∴EF=ECAC12=6,
∴DF=DE﹣EF=9﹣6=3.
故答案为:3.
【点评】本题考查的是三角形中位线定理,角平分线的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
9.(2024秋 凉州区期中)如图,AD是△ABC中BC边上的中线,E,F分别是AB,AD的中点,若△ACD的面积为12cm2,则△DEF的面积为 3 cm2.
【考点】三角形中位线定理;三角形的面积.
【专题】三角形;运算能力;推理能力.
【答案】3
【分析】根据三角形的中线把三角形分成两个面积相等的三角形解答即可.
【解答】解:∵AD是△ABC中BC边上的中线,
∴S△ABD=S△ACD,
∵△ACD的面积为12cm2,
∴,
∵点E是线段AB的中点,
∴,
∵点F是线段AD的中点,
∴.
故答案为:3.
【点评】本题考查三角形中线的定理,三角形的面积,熟练掌握三角形中位线定理是解题的关键.
10.(2024 上海模拟)如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别是三边中点,若CD=5,则EF的长是 5 .
【考点】三角形中位线定理.
【专题】三角形;推理能力.
【答案】5.
【分析】已知CD是Rt△ABC斜边AB的中线,那么AB=2CD;EF是△ABC的中位线,则EF应等于AB的一半.
【解答】解:∵△ABC是直角三角形,CD是斜边的中线,
∴CDAB,
又∵EF是△ABC的中位线,
∴AB=2CD=2×5=10.
∴EF10=5.
故答案为:5.
【点评】此题主要考查了三角形中位线定理以及直角三角形斜边上的中线等知识,用到的知识点为:(1)直角三角形斜边的中线等于斜边的一半;(2)三角形的中位线等于对应边的一半.
三.解答题(共5小题)
11.(2024秋 郸城县期中)如图,在△ABC中,D、E、F分别为边BC、AC、AB的中点,AD、BE、CF相交于点O,AB=6,BC=10,AC=8.试求出线段DE、OF的长.(结果保留根号)
【考点】三角形中位线定理;勾股定理的逆定理.
【专题】等腰三角形与直角三角形;几何直观;推理能力.
【答案】DE=3;OF.
【分析】由AB2+AC2=BC2,可知△ABC是直角三角形,且∠CAB=90°,由题意知,DE为△ABC的中位线,,则,由勾股定理得,,由题意知,O是△ABC的重心,则,求解作答即可.
【解答】解:在△ABC中,AB=6,BC=10,AC=8,
∵62+82=100=102,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,且∠CAB=90°,
∵D、E、F分别为边BC、AC、AB的中点,
∴DE为△ABC的中位线,,
∴,
在直角三角形ACF中,由勾股定理得:,
由题意知,O是△ABC的重心,
∴.
【点评】本题考查了三角形中位线定理,勾股定理的逆定理,熟练掌握勾股定理的逆定理是解题的关键.
12.(2024春 都昌县期末)已知:如图,在△ABC中,中线BE,CD交于点O,F,G分别是OB,OC的中点.连接DF、FG、EG、DE,求证:DF=EG.
【考点】三角形中位线定理.
【专题】证明题.
【答案】见试题解答内容
【分析】根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥BC,DEBC,FG∥BC,FGBC,从而得到DE∥FG且DE=FG,再根据一组对边平行且相等的四边形是平行四边形判断出四边形DEGF是平行四边形,然后根据平行四边形的对边相等证明即可.
【解答】证明:∵BE,CD都是△ABC的中线,
∴DE是△ABC的中位线,
∴DE∥BC,DEBC,
∵F,G分别是OB,OC的中点,
∴FG∥BC,FGBC,
∴DE∥FG且DE=FG,
∴四边形DEGF是平行四边形,
∴DF=EG.
【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的判定与性质,熟记定理并判断出四边形DEGF是平行四边形是解题的关键.
13.(2024春 上城区期末)如图,四边形ABCD为平行四边形,线段AC为对角线,点E、F分别为线段BC、AD的中点,连接EF交AC于点O.
(1)求证:四边形AECF为平行四边形;
(2)若OF=3,求CD的长.
【考点】三角形中位线定理;平行四边形的判定与性质.
【专题】图形的相似;推理能力.
【答案】(1)见解答;
(2)6.
【分析】(1)先根据平行四边形的性质得到AD=BC,AD∥BC,再证明AF=CE,然后根据平行四边形的判定方法得到结论;
(2)先根据平行四边形的性质得到OA=OC,则可判断OF为△ACD的中位线,然后根据三角形中位线定理求解.
【解答】(1)证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
∵点E、F分别为线段BC、AD的中点,
∴AFAD,CEBC,
∴AF=CE,
∵AF∥CE,
∴四边形AECF为平行四边形;
(2)解:∵四边形AECF为平行四边形,
∴OA=OC,
∵AF=DF,
∴OF为△ACD的中位线,
∴CD=2OF=2×3=6.
【点评】本题考查了三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.也考查了平行四边形的判定与性质.
14.(2024春 吉州区期末)如图在△ABC中,AD是△ABC中的∠BAC角平分线,BD⊥AD,点E是边BC的中点,如果AB=6,AC=14,求DE的长.
【考点】三角形中位线定理;全等三角形的判定与性质;等腰三角形的判定与性质.
【专题】三角形;图形的全等;推理能力.
【答案】4.
【分析】延长BD交AC于F,根据垂直的定义得到∠ADB=∠ADF=90°,根据角平分线的定义得到∠BAD=∠FAD,根据全等三角形的性质得到BD=DF,AF=AB=6,求得CF=AC﹣AF=8,根据三角形中位线定理即可得到结论.
【解答】解:延长BD交AC于F,
∵BD⊥AD,
∴∠ADB=∠ADF,
∵AD是△ABC中的∠BAC角平分线,
∴∠BAD=∠FAD,
在△BAD与△FAD中,
,
∴△BAD≌△FAD(ASA),
∴BD=DF,AF=AB=6,
∴CF=AC﹣AF=8,
∵点E是边BC的中点,
∴BE=CE,
∴CF=AC﹣AF=8,
∴DECF=4,
故DE的长为4.
【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,全等三角形的判定和性质,作辅助线构造出以DE为中位线的三角形是解题的关键.
15.(2024春 中宁县期末)如图,点D、E分别是△ABC的边AB、AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若DE=1,求DF的长.
【考点】三角形中位线定理.
【专题】三角形;多边形与平行四边形;推理能力.
【答案】3.
【分析】根据三角形中位线定理得到DE∥BC,BC=2DE=2,根据平行三角形的性质求出EF,计算即可.
【解答】解:∵点D、E分别是边AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,BC=2DE=2,
∵CF∥BE,EF∥BC,
∴四边形FEBC为平行四边形,
∴EF=BC=2,
∴DF=EF+DE=3.
【点评】本题考查的是三角形中位线定理、平行四边形的判定和性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.夯实基础 中位线
一.选择题(共5小题)
1.(2024秋 大连期中)如图,AD,CE都是△ABC的中线,连接ED,△ABC的面积是20cm2,则△CDE的面积是( )
A.2.5cm2 B.5cm2 C.7.5cm2 D.10cm2
2.(2024秋 南安市期中)为了倡导全民健身,某小区在公共活动区域安装了健身器材,其中跷跷板很受欢迎.如图,点O为跷跷板AB的中点,支柱OC垂直于地面,垂足为C,OC=0.6m.当跷跷板的一端A着地时,另一端B离地面的高度为( )
A.0.5m B.0.8m C.1m D.1.2m
3.(2024 兰州)如图,小张想估测被池塘隔开的A,B两处景观之间的距离,他先在AB外取一点C,然后步测出AC,BC的中点D,E,并步测出DE的长约为18m,由此估测A,B之间的距离约为( )
A.18m B.24m C.36m D.54m
4.(2024秋 滕州市期中)如图所示,在边长为6的正方形ABCD中,E为CD上的点,F为BC的中点,过点F作HF⊥EF交AB于点H,点M,N分别是HF和BF的中点,若MN=1,则DE的长为( )
A. B. C.2 D.5
5.(2024春 市中区校级期末)如图,Rt△ABC中,AB=4,AC=3,∠BAC=90°,D,E分别为AB,AC的中点,P为DE上一点,且满足∠EAP=∠ABP,则PE=( )
A. B. C. D.1
二.填空题(共5小题)
6.(2024秋 泉州期中)如图,BD是△ABC的中线,点E是BD的中点,延长AE交BC于点F,若BC=6,则BF的长为 .
7.(2024春 朝阳区校级期末)如图,四边形ABCD中,∠A=60°,AD=2,AB=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为 .
8.(2024春 普陀区期末)如图,在△ABC中,D、E分别是AB、AC的中点,∠ACB的平分线交DE于点F,如果AC=12,BC=18,那么DF的长为 .
9.(2024秋 凉州区期中)如图,AD是△ABC中BC边上的中线,E,F分别是AB,AD的中点,若△ACD的面积为12cm2,则△DEF的面积为 cm2.
10.(2024 上海模拟)如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别是三边中点,若CD=5,则EF的长是 .
三.解答题(共5小题)
11.(2024秋 郸城县期中)如图,在△ABC中,D、E、F分别为边BC、AC、AB的中点,AD、BE、CF相交于点O,AB=6,BC=10,AC=8.试求出线段DE、OF的长.(结果保留根号)
12.(2024春 都昌县期末)已知:如图,在△ABC中,中线BE,CD交于点O,F,G分别是OB,OC的中点.连接DF、FG、EG、DE,求证:DF=EG.
13.(2024春 上城区期末)如图,四边形ABCD为平行四边形,线段AC为对角线,点E、F分别为线段BC、AD的中点,连接EF交AC于点O.
(1)求证:四边形AECF为平行四边形;
(2)若OF=3,求CD的长.
14.(2024春 吉州区期末)如图在△ABC中,AD是△ABC中的∠BAC角平分线,BD⊥AD,点E是边BC的中点,如果AB=6,AC=14,求DE的长.
15.(2024春 中宁县期末)如图,点D、E分别是△ABC的边AB、AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若DE=1,求DF的长.
预习衔接.夯实基础 中位线
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 大连期中)如图,AD,CE都是△ABC的中线,连接ED,△ABC的面积是20cm2,则△CDE的面积是( )
A.2.5cm2 B.5cm2 C.7.5cm2 D.10cm2
【考点】三角形中位线定理;三角形的面积.
【专题】三角形;运算能力.
【答案】A
【分析】三角形的中线将三角形分成面积相等的两部分,三次利用该定理即可求得结果.
【解答】解:∵AD是△ABC的中线,
∴,
∵CE是△ABC的中线,
∴DE为△ABD的中线,
即,
∵DE为△BEC的中线,
∴S.
故选:A.
【点评】本题考查了利用三角形的中线求三角形的面积,掌握三角形中线的性质是解题的关键.
2.(2024秋 南安市期中)为了倡导全民健身,某小区在公共活动区域安装了健身器材,其中跷跷板很受欢迎.如图,点O为跷跷板AB的中点,支柱OC垂直于地面,垂足为C,OC=0.6m.当跷跷板的一端A着地时,另一端B离地面的高度为( )
A.0.5m B.0.8m C.1m D.1.2m
【考点】三角形中位线定理;相似三角形的判定与性质.
【专题】三角形;图形的相似.
【答案】D
【分析】过点B作BD垂直底面于点D,判断出OC是△ABD的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半可得BD=2OC.
【解答】解:如图,过点B作BD垂直底面于点D,
∵BD⊥AD,OC⊥AD,
∴BD∥OC,
∴△AOC∽△ABD,
∴,
∵点O为跷跷板AB的中点,
∴ACAD,
∴OC是△ABD的中位线,
∵OC=0.6m,
∴BD=2OC=1.2m,
故选:D.
【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,相似三角形的判定与性质,熟记定理是解题的关键.
3.(2024 兰州)如图,小张想估测被池塘隔开的A,B两处景观之间的距离,他先在AB外取一点C,然后步测出AC,BC的中点D,E,并步测出DE的长约为18m,由此估测A,B之间的距离约为( )
A.18m B.24m C.36m D.54m
【考点】三角形中位线定理.
【专题】三角形;推理能力.
【答案】C
【分析】依据题意,由D,E分别是边AC,BC的中点,首先判定DE是三角形的中位线,然后根据三角形的中位线定理求得AB的值即可
【解答】解:∵D、E分别是AC、BC的中点,
∴DE是△ABC的中位线.
∴根据三角形的中位线定理,得:AB=2DE=36m.
故选:C.
【点评】本题主要考查了三角形中位线定理的运用,解题时要能熟练掌握并能灵活运用三角形中位线定理是关键.
4.(2024秋 滕州市期中)如图所示,在边长为6的正方形ABCD中,E为CD上的点,F为BC的中点,过点F作HF⊥EF交AB于点H,点M,N分别是HF和BF的中点,若MN=1,则DE的长为( )
A. B. C.2 D.5
【考点】三角形中位线定理;正方形的性质;相似三角形的判定与性质.
【专题】三角形;矩形 菱形 正方形;图形的相似;推理能力.
【答案】B
【分析】根据三角形的中位线定理得HB=2MN=2,再由正方形的性质得由HF⊥EF,得∠HFE=90°,推导出∠BFH=∠CEF,进而证明△BFH∽△CEF,得,则CE=4.5,于是得到问题的答案.
【解答】解:∵点M,N分别是HF和BF的中点,
∴BN=FN,HM=FM,
∴MN是△HBF的中位线,
∵MN=1,
∴BH=2MN=2,
∵四边形ABCD是正方形,
∴BC=CD=6,∠B=∠C=90°,
∵F为BC的中点,
∴CF=BF=3,
∵HF⊥EF,
∴∠HFE=90°,
∴∠BFH=∠CEF,
∴△BFH∽△CEF,
∴,
∴,
∴CE=4.5,
∴,
故选:B.
【点评】此题重点考查正方形的性质,直角三角形的两个锐角互余、相似三角形的判定与性质、三角形的中位线定理等知识,证明△BFH∽△CEF是解题的关键.
5.(2024春 市中区校级期末)如图,Rt△ABC中,AB=4,AC=3,∠BAC=90°,D,E分别为AB,AC的中点,P为DE上一点,且满足∠EAP=∠ABP,则PE=( )
A. B. C. D.1
【考点】三角形中位线定理;全等三角形的判定与性质.
【专题】等腰三角形与直角三角形;推理能力.
【答案】A
【分析】根据直角三角形斜边上的中线的性质求出DP,根据勾股定理求出BC,根据三角形中位线定理求出DE,进而求出PE.
【解答】解:∵∠BAC=90°,
∴∠BAP+∠EAP=90°,
∵∠EAP=∠ABP,
∴∠ABP+∠EAP=90°,
∴∠APB=90°,
∵D为AB的中点,
∴DPAB=2,
在Rt△ABC中,AB=4,AC=3,
则BC5,
∵D,E分别为AB,AC的中点,
∴DE是△ABC的中位线,
∴DEBC,
∴PE=DE﹣DP,
故选:A.
【点评】本题考查的是三角形中位线定理,熟记三角形中位线等于第三边的一半是解题的关键.
二.填空题(共5小题)
6.(2024秋 泉州期中)如图,BD是△ABC的中线,点E是BD的中点,延长AE交BC于点F,若BC=6,则BF的长为 2 .
【考点】三角形中位线定理.
【专题】三角形;运算能力.
【答案】2.
【分析】取FC的中点H,连接DH,根据三角形中位线定理解答即可.
【解答】解:取FC的中点H,连接DH,
∵CD=DA,
∴DH是△ACF的中位线,
∴DH∥AF,
∵BE=ED,
∴EF是△BEF的中位线,
∴BF=FH,
∴,
故答案为:2.
【点评】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
7.(2024春 朝阳区校级期末)如图,四边形ABCD中,∠A=60°,AD=2,AB=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为 .
【考点】三角形中位线定理.
【专题】三角形;推理能力.
【答案】.
【分析】根据三角形的中位线定理得出 ,从而可知DN最大时,EF最大,因为N与B重合时DN最大,此时根据勾股定理求得DN,从而求得EF的最大值.连接DB,过点D作DH⊥AB 交AB于点H,再利用直角三角形的性质和勾股定理求解即可.
【解答】解:∵ED=EM,MF=FN,,
∴DN最大时,EF最大,
∴N与B重合时DN=DB最大,
在Rt△ADH中,
∵∠A=60°,
∴∠ADH=30°,
∴,,
∴BH=AB﹣AH=3﹣1=2,
∴,
∴.
故答案为:.
【点评】本题考查了三角形的中位线定理,勾股定理,含30度角的直角三角形的性质,利用三角形中位线求得是解题的关键.
8.(2024春 普陀区期末)如图,在△ABC中,D、E分别是AB、AC的中点,∠ACB的平分线交DE于点F,如果AC=12,BC=18,那么DF的长为 3 .
【考点】三角形中位线定理;角平分线的性质.
【专题】线段、角、相交线与平行线;三角形;运算能力;推理能力.
【答案】3.
【分析】根据三角形中位线定理得到DE∥BC,DEBC,求出EF,进而求出DF.
【解答】解:∵CF是∠ABC的平分线,
∴∠ACF=∠FCB,
∵点D、E分别为边AB、AC的中点,
∴DE∥BC,DEBC9,
∴∠EFC=∠FCB,
∴∠ACF=∠EFC,
∴EF=ECAC12=6,
∴DF=DE﹣EF=9﹣6=3.
故答案为:3.
【点评】本题考查的是三角形中位线定理,角平分线的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
9.(2024秋 凉州区期中)如图,AD是△ABC中BC边上的中线,E,F分别是AB,AD的中点,若△ACD的面积为12cm2,则△DEF的面积为 3 cm2.
【考点】三角形中位线定理;三角形的面积.
【专题】三角形;运算能力;推理能力.
【答案】3
【分析】根据三角形的中线把三角形分成两个面积相等的三角形解答即可.
【解答】解:∵AD是△ABC中BC边上的中线,
∴S△ABD=S△ACD,
∵△ACD的面积为12cm2,
∴,
∵点E是线段AB的中点,
∴,
∵点F是线段AD的中点,
∴.
故答案为:3.
【点评】本题考查三角形中线的定理,三角形的面积,熟练掌握三角形中位线定理是解题的关键.
10.(2024 上海模拟)如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别是三边中点,若CD=5,则EF的长是 5 .
【考点】三角形中位线定理.
【专题】三角形;推理能力.
【答案】5.
【分析】已知CD是Rt△ABC斜边AB的中线,那么AB=2CD;EF是△ABC的中位线,则EF应等于AB的一半.
【解答】解:∵△ABC是直角三角形,CD是斜边的中线,
∴CDAB,
又∵EF是△ABC的中位线,
∴AB=2CD=2×5=10.
∴EF10=5.
故答案为:5.
【点评】此题主要考查了三角形中位线定理以及直角三角形斜边上的中线等知识,用到的知识点为:(1)直角三角形斜边的中线等于斜边的一半;(2)三角形的中位线等于对应边的一半.
三.解答题(共5小题)
11.(2024秋 郸城县期中)如图,在△ABC中,D、E、F分别为边BC、AC、AB的中点,AD、BE、CF相交于点O,AB=6,BC=10,AC=8.试求出线段DE、OF的长.(结果保留根号)
【考点】三角形中位线定理;勾股定理的逆定理.
【专题】等腰三角形与直角三角形;几何直观;推理能力.
【答案】DE=3;OF.
【分析】由AB2+AC2=BC2,可知△ABC是直角三角形,且∠CAB=90°,由题意知,DE为△ABC的中位线,,则,由勾股定理得,,由题意知,O是△ABC的重心,则,求解作答即可.
【解答】解:在△ABC中,AB=6,BC=10,AC=8,
∵62+82=100=102,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,且∠CAB=90°,
∵D、E、F分别为边BC、AC、AB的中点,
∴DE为△ABC的中位线,,
∴,
在直角三角形ACF中,由勾股定理得:,
由题意知,O是△ABC的重心,
∴.
【点评】本题考查了三角形中位线定理,勾股定理的逆定理,熟练掌握勾股定理的逆定理是解题的关键.
12.(2024春 都昌县期末)已知:如图,在△ABC中,中线BE,CD交于点O,F,G分别是OB,OC的中点.连接DF、FG、EG、DE,求证:DF=EG.
【考点】三角形中位线定理.
【专题】证明题.
【答案】见试题解答内容
【分析】根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥BC,DEBC,FG∥BC,FGBC,从而得到DE∥FG且DE=FG,再根据一组对边平行且相等的四边形是平行四边形判断出四边形DEGF是平行四边形,然后根据平行四边形的对边相等证明即可.
【解答】证明:∵BE,CD都是△ABC的中线,
∴DE是△ABC的中位线,
∴DE∥BC,DEBC,
∵F,G分别是OB,OC的中点,
∴FG∥BC,FGBC,
∴DE∥FG且DE=FG,
∴四边形DEGF是平行四边形,
∴DF=EG.
【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的判定与性质,熟记定理并判断出四边形DEGF是平行四边形是解题的关键.
13.(2024春 上城区期末)如图,四边形ABCD为平行四边形,线段AC为对角线,点E、F分别为线段BC、AD的中点,连接EF交AC于点O.
(1)求证:四边形AECF为平行四边形;
(2)若OF=3,求CD的长.
【考点】三角形中位线定理;平行四边形的判定与性质.
【专题】图形的相似;推理能力.
【答案】(1)见解答;
(2)6.
【分析】(1)先根据平行四边形的性质得到AD=BC,AD∥BC,再证明AF=CE,然后根据平行四边形的判定方法得到结论;
(2)先根据平行四边形的性质得到OA=OC,则可判断OF为△ACD的中位线,然后根据三角形中位线定理求解.
【解答】(1)证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
∵点E、F分别为线段BC、AD的中点,
∴AFAD,CEBC,
∴AF=CE,
∵AF∥CE,
∴四边形AECF为平行四边形;
(2)解:∵四边形AECF为平行四边形,
∴OA=OC,
∵AF=DF,
∴OF为△ACD的中位线,
∴CD=2OF=2×3=6.
【点评】本题考查了三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.也考查了平行四边形的判定与性质.
14.(2024春 吉州区期末)如图在△ABC中,AD是△ABC中的∠BAC角平分线,BD⊥AD,点E是边BC的中点,如果AB=6,AC=14,求DE的长.
【考点】三角形中位线定理;全等三角形的判定与性质;等腰三角形的判定与性质.
【专题】三角形;图形的全等;推理能力.
【答案】4.
【分析】延长BD交AC于F,根据垂直的定义得到∠ADB=∠ADF=90°,根据角平分线的定义得到∠BAD=∠FAD,根据全等三角形的性质得到BD=DF,AF=AB=6,求得CF=AC﹣AF=8,根据三角形中位线定理即可得到结论.
【解答】解:延长BD交AC于F,
∵BD⊥AD,
∴∠ADB=∠ADF,
∵AD是△ABC中的∠BAC角平分线,
∴∠BAD=∠FAD,
在△BAD与△FAD中,
,
∴△BAD≌△FAD(ASA),
∴BD=DF,AF=AB=6,
∴CF=AC﹣AF=8,
∵点E是边BC的中点,
∴BE=CE,
∴CF=AC﹣AF=8,
∴DECF=4,
故DE的长为4.
【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,全等三角形的判定和性质,作辅助线构造出以DE为中位线的三角形是解题的关键.
15.(2024春 中宁县期末)如图,点D、E分别是△ABC的边AB、AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若DE=1,求DF的长.
【考点】三角形中位线定理.
【专题】三角形;多边形与平行四边形;推理能力.
【答案】3.
【分析】根据三角形中位线定理得到DE∥BC,BC=2DE=2,根据平行三角形的性质求出EF,计算即可.
【解答】解:∵点D、E分别是边AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,BC=2DE=2,
∵CF∥BE,EF∥BC,
∴四边形FEBC为平行四边形,
∴EF=BC=2,
∴DF=EF+DE=3.
【点评】本题考查的是三角形中位线定理、平行四边形的判定和性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
