23.5位似图形(预习衔接.夯实基础.含解析)-2025-2026学年九年级上册数学华东师大版
文档属性
| 名称 | 23.5位似图形(预习衔接.夯实基础.含解析)-2025-2026学年九年级上册数学华东师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 476.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 21:17:08 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
预习衔接.夯实基础 位似图形
一.选择题(共5小题)
1.(2024秋 宝安区期中)如图,已知△A'B'C'与△ABC是以点O为位似中心的位似图形,位似比为3:5,下列说法错误的是( )
A.AC∥A'C'
B.S△A'B′C′:S△ABC=9:25
C.△BCO~△B'C'O
D.OB′:BB′=5:3
2.(2024秋 大连期中)利用位似可以设计有立体感的美术字.如图,是某同学以点O为位似中心,设计“MATH”中字母“M”美术字的一种方法.若AB=5,A'B'=3,则的值为( )
A. B. C. D.
3.(2024秋 铁西区期中)如图,△ABC与△DEF位似,点O是位似中心,若OA:AD=1:2,DF﹣AC=8,则DF+AC为( )
A.8 B.12 C.16 D.18
4.(2024秋 武强县期中)如图,△ABC与△DEF是位似图形,点O是位似中心.若OA=2AD,△ABC的周长为4,则△DEF的周长为( )
A.6 B.8 C.9 D.12
5.(2024秋 饶阳县期中)如图,△ABC与△A′B′C′位似,点O为位似中心,且点O在边AA′上.若AA′=3OA,BC=5,则B′C′的长为( )
A.5 B.10 C.15 D.20
二.填空题(共5小题)
6.(2024秋 长春期中)如图,以点A为位似中心的四边形ABCD和四边形AB′C′D′面积比为9:4,若AB=6,则AB′的长为 .
7.(2024秋 农安县期中)按下列方法,将△ABC的三边缩小为原来的,如图所示,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F,连接DE,EF,FD得到△DEF,则下列说法正确的序号有 .
①△ABC与△DEF是位似图形;
②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长之比为2:1;
④△ABC与△DEF的面积之比为2:1.
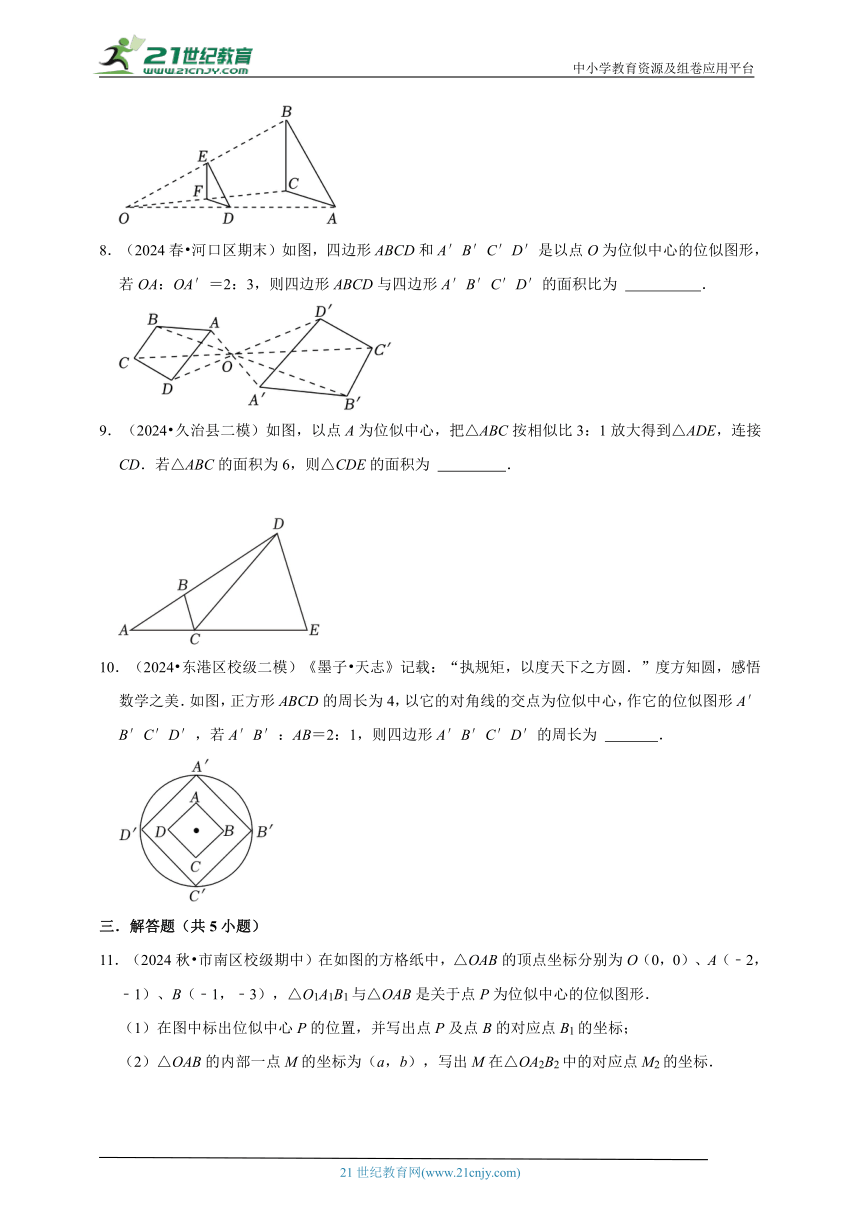
8.(2024春 河口区期末)如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′=2:3,则四边形ABCD与四边形A′B′C′D′的面积比为 .
9.(2024 久治县二模)如图,以点A为位似中心,把△ABC按相似比3:1放大得到△ADE,连接CD.若△ABC的面积为6,则△CDE的面积为 .
10.(2024 东港区校级二模)《墨子 天志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形ABCD的周长为4,以它的对角线的交点为位似中心,作它的位似图形A′B′C′D′,若A′B′:AB=2:1,则四边形A′B′C′D′的周长为 .
三.解答题(共5小题)
11.(2024秋 市南区校级期中)在如图的方格纸中,△OAB的顶点坐标分别为O(0,0)、A(﹣2,﹣1)、B(﹣1,﹣3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.
(1)在图中标出位似中心P的位置,并写出点P及点B的对应点B1的坐标;
(2)△OAB的内部一点M的坐标为(a,b),写出M在△OA2B2中的对应点M2的坐标.
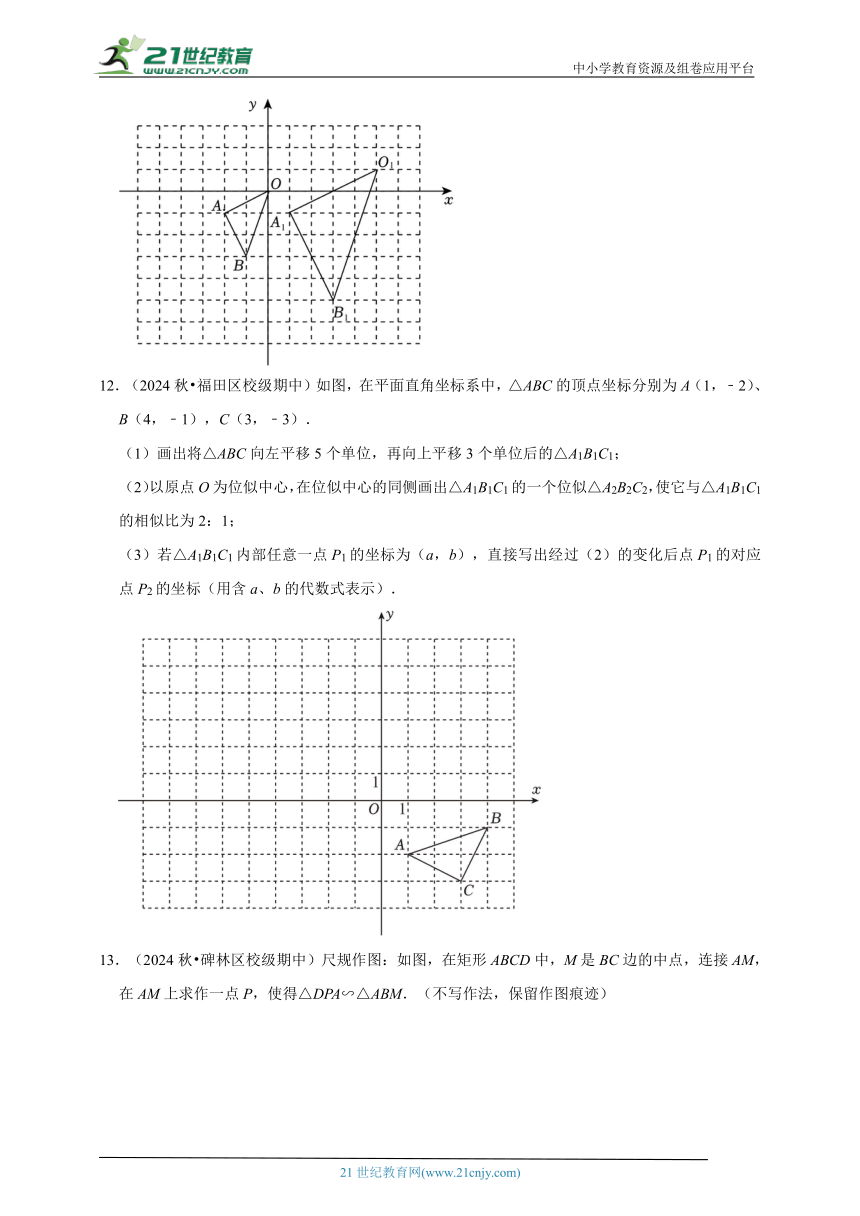
12.(2024秋 福田区校级期中)如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(1,﹣2)、B(4,﹣1),C(3,﹣3).
(1)画出将△ABC向左平移5个单位,再向上平移3个单位后的△A1B1C1;
(2)以原点O为位似中心,在位似中心的同侧画出△A1B1C1的一个位似△A2B2C2,使它与△A1B1C1的相似比为2:1;
(3)若△A1B1C1内部任意一点P1的坐标为(a,b),直接写出经过(2)的变化后点P1的对应点P2的坐标(用含a、b的代数式表示).
13.(2024秋 碑林区校级期中)尺规作图:如图,在矩形ABCD中,M是BC边的中点,连接AM,在AM上求作一点P,使得△DPA∽△ABM.(不写作法,保留作图痕迹)
14.(2024秋 碑林区校级期中)如图,在平面直角坐标系中,△ABC的顶点均在网格格点上,且点A、B、C的坐标分别为A(3,0),B(4,2),C(2,4).
(1)以点O为位似中心,在第一象限画出△ABC的位似图形△A1B1C1,使△A1B1C1与△ABC的相似比为2:1;
(2)在(1)的条件下,求△A1B1C1的面积.
15.(2024秋 泰兴市期中)如图,在△ABC中,AB=6,AC=10,点D是AB的中点.请用无刻度直尺和圆规在AC边上作出点E,使△ADE∽△ACB,并求AE的长.
预习衔接.夯实基础 位似图形
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 宝安区期中)如图,已知△A'B'C'与△ABC是以点O为位似中心的位似图形,位似比为3:5,下列说法错误的是( )
A.AC∥A'C'
B.S△A'B′C′:S△ABC=9:25
C.△BCO~△B'C'O
D.OB′:BB′=5:3
【考点】位似变换;平行线的判定.
【专题】图形的相似;几何直观;应用意识.
【答案】D
【分析】结合位似图形的定义、相似三角形的判定与性质逐项判断即可.
【解答】解:∵△A'B'C'与△ABC是以点O为位似中心的位似图形,位似比为3:5,
∴AC∥A'C',△A'B'C'∽△ABC,且相似比为3:5,
∴S△A'B'C':S△ABC=9:25.
故A,B选项正确,不符合题意;
∵△A'B'C'与△ABC是以点O为位似中心的位似图形,
∴BC∥B'C',
∴∠C'B'O=∠CBO,∠B'C'O=∠BCO,
∴△BCO~△B'C'O,
故C选项正确,不符合题意;
∵△A'B'C'与△ABC是以点O为位似中心的位似图形,位似比为3:5,
∴OB':OB=3:5,
∴OB′:BB′=3:2.
故D选项不正确,符合题意.
故选:D.
【点评】本题考查位似变换、平行线的判定,熟练掌握位似图形的定义、相似三角形的判定与性质是解答本题的关键.
2.(2024秋 大连期中)利用位似可以设计有立体感的美术字.如图,是某同学以点O为位似中心,设计“MATH”中字母“M”美术字的一种方法.若AB=5,A'B'=3,则的值为( )
A. B. C. D.
【考点】位似变换.
【专题】图形的相似;运算能力.
【答案】B
【分析】根据位似图形的性质知:,代入数值求解即可.
【解答】解:∵该图形是以点O为位似中心,
∴.
∵AB=5,A'B'=3,
∴.
故选:B.
【点评】本题考查的是位似变换.位似变换的两个图形相似.根据相似多边形对应边成比例.
3.(2024秋 铁西区期中)如图,△ABC与△DEF位似,点O是位似中心,若OA:AD=1:2,DF﹣AC=8,则DF+AC为( )
A.8 B.12 C.16 D.18
【考点】位似变换.
【专题】图形的相似;几何直观;推理能力.
【答案】C
【分析】首先根据题意可知,再结合位似图形的性质可得,结合DF﹣AC=8解得AC、DF的值,进而可得答案.
【解答】解:△ABC与△DEF位似,点O是位似中心,OA:AD=1:2,
∴,
∴,
∴DF=3AC,
∵DF﹣AC=8,
∴3AC﹣AC=2AC=8,
解得AC=4,
∴DF=3AC=12,
∴DF+AC=12+4=16.
故选:C.
【点评】本题主要考查了位似变换,熟练掌握位似图形的定义和性质是解题关键.
4.(2024秋 武强县期中)如图,△ABC与△DEF是位似图形,点O是位似中心.若OA=2AD,△ABC的周长为4,则△DEF的周长为( )
A.6 B.8 C.9 D.12
【考点】位似变换.
【专题】图形的相似;应用意识.
【答案】A
【分析】结合题意可得△ABC与△DEF的位似比为2:3,则△ABC与△DEF的周长比为2:3,进而可得答案.
【解答】解:∵OA=2AD,
∴OA:OD=2:3.
∵△ABC与△DEF是位似图形,点O是位似中心,
∴△ABC与△DEF的位似比为2:3,
∴△ABC与△DEF的周长比为2:3.
∵△ABC的周长为4,
∴△DEF的周长为6.
故选:A.
【点评】本题考查位似变换,熟练掌握位似的性质是解答本题的关键.
5.(2024秋 饶阳县期中)如图,△ABC与△A′B′C′位似,点O为位似中心,且点O在边AA′上.若AA′=3OA,BC=5,则B′C′的长为( )
A.5 B.10 C.15 D.20
【考点】位似变换.
【专题】图形的相似;推理能力.
【答案】B
【分析】根据位似图形的定义得到AC∥A′C′,得到△AOC∽△A′OC′,根据相似三角形的性质求出,进而求出,计算即可.
【解答】解:∵AA′=3OA,
∴OA:OA′=1:2,
∵△ABC与△A′B′C′位似,点O为位似中心,
∴AC∥A′C′,
∴△AOC∽△A′OC′,
∴,
∴,
∵BC=5,
∴B′C′=10,
故选:B.
【点评】本题考查的是位似变换,掌握位似图形的定义、相似三角形的性质是解题的关键.
二.填空题(共5小题)
6.(2024秋 长春期中)如图,以点A为位似中心的四边形ABCD和四边形AB′C′D′面积比为9:4,若AB=6,则AB′的长为 4 .
【考点】位似变换.
【专题】图形的相似;几何直观;应用意识.
【答案】4.
【分析】由题意得四边形ABCD与四边形AB′C′D′的相似比为3:2,即AB:AB'=3:2,进而可得答案.
【解答】解:∵以点A为位似中心的四边形ABCD和四边形AB′C′D′面积比为9:4,
∴四边形ABCD与四边形AB′C′D′的相似比为3:2,
∴AB:AB'=3:2,
∵AB=6,
∴AB′=4.
故答案为:4.
【点评】本题考查位似变换,熟练掌握位似的性质是解答本题的关键.
7.(2024秋 农安县期中)按下列方法,将△ABC的三边缩小为原来的,如图所示,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F,连接DE,EF,FD得到△DEF,则下列说法正确的序号有 ①②③ .
①△ABC与△DEF是位似图形;
②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长之比为2:1;
④△ABC与△DEF的面积之比为2:1.
【考点】位似变换.
【专题】图形的相似;推理能力.
【答案】①②③.
【分析】根据位似变换的定义和性质判断即可.
【解答】解:由题意可知:△ABC与△DEF是位似图形,故①说法正确;
△ABC与△DEF是相似图形,故②说法正确;
△ABC与△DEF的周长之比为2:1,故③说法正确;
△ABC与△DEF的面积之比为4:1,故④说法错误;
故答案为:①②③.
【点评】本题考查的是位似变换,位似是相似的特殊形式,位似比等于相似比,其对应的面积比等于相似比的平方.
8.(2024春 河口区期末)如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′=2:3,则四边形ABCD与四边形A′B′C′D′的面积比为 4:9 .
【考点】位似变换.
【专题】图形的相似;几何直观;推理能力.
【答案】4:9.
【分析】根据位似图形的性质和OA:OA′=2:3得到四边形ABCD和A′B′C′D′的相似比为2:3,即可得到答案.
【解答】解:∵四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,且OA:OA′=2:3,
∴四边形ABCD和A′B′C′D′的相似比为2:3,
∴四边形与四边形的面积比为4:9.
故答案为4:9.
【点评】此题考查了位似变换,掌握位似图形与相似图形的关系、相似多边形的性质是解题的关键.
9.(2024 久治县二模)如图,以点A为位似中心,把△ABC按相似比3:1放大得到△ADE,连接CD.若△ABC的面积为6,则△CDE的面积为 36 .
【考点】位似变换.
【专题】图形的相似;运算能力.
【答案】36.
【分析】根据位似变换的性质及三角形的面积公式求解.
【解答】解:∵△ABC按相似比3:1放大得到△ADE,
∴△ABC与△ADE的面积比为9:1,AB:DB=1:2,
∴△ADE的面积为54,△BDC的面积为12,
∴△CDE的面积为:54﹣6﹣12=36,
故答案为:36.
【点评】本题考查了位似变换,掌握位似变换的性质及三角形的面积公式的解题的关键.
10.(2024 东港区校级二模)《墨子 天志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形ABCD的周长为4,以它的对角线的交点为位似中心,作它的位似图形A′B′C′D′,若A′B′:AB=2:1,则四边形A′B′C′D′的周长为 8 .
【考点】位似变换;正方形的性质.
【专题】图形的相似;运算能力;推理能力.
【答案】8.
【分析】利用“相似多边形的周长之比等于相似比”求得答案.
【解答】解:根据题意知,正方形ABCD∽正方形A'B'C'D',且相似比为:AB:A'B'=2:1,
∴正方形ABCD的周长:四边形A'B'C'D'的周长=AB:A'B'=2:1.
∵正方形ABCD的周长为4,
∴四边形A′B′C′D′的周长为8.
故答案为:8.
【点评】本题考查位似变换,相似多边形的性质,圆的周长等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
三.解答题(共5小题)
11.(2024秋 市南区校级期中)在如图的方格纸中,△OAB的顶点坐标分别为O(0,0)、A(﹣2,﹣1)、B(﹣1,﹣3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.
(1)在图中标出位似中心P的位置,并写出点P及点B的对应点B1的坐标;
(2)△OAB的内部一点M的坐标为(a,b),写出M在△OA2B2中的对应点M2的坐标.
【考点】作图﹣位似变换.
【专题】作图题;平移、旋转与对称;几何直观.
【答案】(1)画图见解答;点P的坐标为(﹣5,﹣1),点B1的坐标为(3,﹣5).
(2)点M2的坐标为(2a+5,2b+1).
【分析】(1)连接O1O,A1A,B1B,并分别延长相交于点P,则点P即为所求,由图可得答案.
(2)根据题意可得点M2的坐标为(2a+5,2b+1).
【解答】解:(1)如图,连接O1O,A1A,B1B,并分别延长相交于点P,
则点P即为所求.
由图可得,点P的坐标为(﹣5,﹣1),点B1的坐标为(3,﹣5).
(2)由题意得,点M2的坐标为(2a+5,2b+1).
【点评】本题考查作图﹣位似变换,熟练掌握位似的性质是解答本题的关键.
12.(2024秋 福田区校级期中)如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(1,﹣2)、B(4,﹣1),C(3,﹣3).
(1)画出将△ABC向左平移5个单位,再向上平移3个单位后的△A1B1C1;
(2)以原点O为位似中心,在位似中心的同侧画出△A1B1C1的一个位似△A2B2C2,使它与△A1B1C1的相似比为2:1;
(3)若△A1B1C1内部任意一点P1的坐标为(a,b),直接写出经过(2)的变化后点P1的对应点P2的坐标(用含a、b的代数式表示).
【考点】作图﹣位似变换;作图﹣平移变换.
【专题】作图题;平移、旋转与对称;图形的相似;几何直观.
【答案】(1)见解答;
(2)见解答;
(3)点P2的坐标为:(2a,2b).
【分析】(1)利用平移的性质得出对应点坐标位置进而得出答案;
(2)画出一个以点O为位似中心的△A2B2C2,使得△A2B2C2与△A1B1C1的相似比为2即可;
(3)根据相似比即可求得.
【解答】解:(1)如图所示,△A1B1C1为所求三角形.
(2)如图所示,△A2B2C2为所求角形.
(3)由题意可知△A2B2C2∽△A2B2C2,且相似比为2:1,
∴当点P1的坐标为(a,b)时,对应点P2的坐标为:(2a,2b).
【点评】本题考查了平移作图,画位似图形,数形结合是解题的关键.
13.(2024秋 碑林区校级期中)尺规作图:如图,在矩形ABCD中,M是BC边的中点,连接AM,在AM上求作一点P,使得△DPA∽△ABM.(不写作法,保留作图痕迹)
【考点】作图﹣相似变换;矩形的性质.
【专题】作图题;几何直观.
【答案】见解析.
【分析】过点D作DP⊥AM于P,则点P即为所求.
【解答】解:如图所示,点P即为所求.
【点评】本题考查了作图﹣相似变换,矩形的性质,正确地作出图形是解题的关键.
14.(2024秋 碑林区校级期中)如图,在平面直角坐标系中,△ABC的顶点均在网格格点上,且点A、B、C的坐标分别为A(3,0),B(4,2),C(2,4).
(1)以点O为位似中心,在第一象限画出△ABC的位似图形△A1B1C1,使△A1B1C1与△ABC的相似比为2:1;
(2)在(1)的条件下,求△A1B1C1的面积.
【考点】作图﹣位似变换.
【专题】作图题;图形的相似;几何直观;运算能力.
【答案】(1)见解答.
(2)12.
【分析】(1)根据位似的性质作图即可.
(2)利用割补法求三角形的面积即可.
【解答】解:(1)如图所示,△A1B1C1即为所求.
(2)△A1B1C1的面积为24﹣4﹣8=12.
【点评】本题考查作图﹣位似变换,熟练掌握位似的性质是解答本题的关键.
15.(2024秋 泰兴市期中)如图,在△ABC中,AB=6,AC=10,点D是AB的中点.请用无刻度直尺和圆规在AC边上作出点E,使△ADE∽△ACB,并求AE的长.
【考点】作图﹣相似变换.
【专题】图形的相似;尺规作图;几何直观;推理能力.
【答案】作图见解析,AE=1.8.
【分析】以C为圆心,DA为半径作弧与CB,CA相交,两交点确定线段a,以D为圆心,DA为半径作弧,以A为圆心,线段a为半径作弧,两弧交于一点,连接点D与交点并延长与CA相交,即为点E;由△ADE∽△ACB得到,代入数据即可求解AE.
【解答】解:作图如下;
∵△ADE∽△ACB,
∴,
∵AB=6,AC=10,点D是AB的中点,
∴AD=3,
∴,
解得:AE=1.8.
【点评】本题考查了作图﹣相似变换,熟练掌握作一个角等于已知角的方法是解答本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.夯实基础 位似图形
一.选择题(共5小题)
1.(2024秋 宝安区期中)如图,已知△A'B'C'与△ABC是以点O为位似中心的位似图形,位似比为3:5,下列说法错误的是( )
A.AC∥A'C'
B.S△A'B′C′:S△ABC=9:25
C.△BCO~△B'C'O
D.OB′:BB′=5:3
2.(2024秋 大连期中)利用位似可以设计有立体感的美术字.如图,是某同学以点O为位似中心,设计“MATH”中字母“M”美术字的一种方法.若AB=5,A'B'=3,则的值为( )
A. B. C. D.
3.(2024秋 铁西区期中)如图,△ABC与△DEF位似,点O是位似中心,若OA:AD=1:2,DF﹣AC=8,则DF+AC为( )
A.8 B.12 C.16 D.18
4.(2024秋 武强县期中)如图,△ABC与△DEF是位似图形,点O是位似中心.若OA=2AD,△ABC的周长为4,则△DEF的周长为( )
A.6 B.8 C.9 D.12
5.(2024秋 饶阳县期中)如图,△ABC与△A′B′C′位似,点O为位似中心,且点O在边AA′上.若AA′=3OA,BC=5,则B′C′的长为( )
A.5 B.10 C.15 D.20
二.填空题(共5小题)
6.(2024秋 长春期中)如图,以点A为位似中心的四边形ABCD和四边形AB′C′D′面积比为9:4,若AB=6,则AB′的长为 .
7.(2024秋 农安县期中)按下列方法,将△ABC的三边缩小为原来的,如图所示,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F,连接DE,EF,FD得到△DEF,则下列说法正确的序号有 .
①△ABC与△DEF是位似图形;
②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长之比为2:1;
④△ABC与△DEF的面积之比为2:1.
8.(2024春 河口区期末)如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′=2:3,则四边形ABCD与四边形A′B′C′D′的面积比为 .
9.(2024 久治县二模)如图,以点A为位似中心,把△ABC按相似比3:1放大得到△ADE,连接CD.若△ABC的面积为6,则△CDE的面积为 .
10.(2024 东港区校级二模)《墨子 天志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形ABCD的周长为4,以它的对角线的交点为位似中心,作它的位似图形A′B′C′D′,若A′B′:AB=2:1,则四边形A′B′C′D′的周长为 .
三.解答题(共5小题)
11.(2024秋 市南区校级期中)在如图的方格纸中,△OAB的顶点坐标分别为O(0,0)、A(﹣2,﹣1)、B(﹣1,﹣3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.
(1)在图中标出位似中心P的位置,并写出点P及点B的对应点B1的坐标;
(2)△OAB的内部一点M的坐标为(a,b),写出M在△OA2B2中的对应点M2的坐标.
12.(2024秋 福田区校级期中)如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(1,﹣2)、B(4,﹣1),C(3,﹣3).
(1)画出将△ABC向左平移5个单位,再向上平移3个单位后的△A1B1C1;
(2)以原点O为位似中心,在位似中心的同侧画出△A1B1C1的一个位似△A2B2C2,使它与△A1B1C1的相似比为2:1;
(3)若△A1B1C1内部任意一点P1的坐标为(a,b),直接写出经过(2)的变化后点P1的对应点P2的坐标(用含a、b的代数式表示).
13.(2024秋 碑林区校级期中)尺规作图:如图,在矩形ABCD中,M是BC边的中点,连接AM,在AM上求作一点P,使得△DPA∽△ABM.(不写作法,保留作图痕迹)
14.(2024秋 碑林区校级期中)如图,在平面直角坐标系中,△ABC的顶点均在网格格点上,且点A、B、C的坐标分别为A(3,0),B(4,2),C(2,4).
(1)以点O为位似中心,在第一象限画出△ABC的位似图形△A1B1C1,使△A1B1C1与△ABC的相似比为2:1;
(2)在(1)的条件下,求△A1B1C1的面积.
15.(2024秋 泰兴市期中)如图,在△ABC中,AB=6,AC=10,点D是AB的中点.请用无刻度直尺和圆规在AC边上作出点E,使△ADE∽△ACB,并求AE的长.
预习衔接.夯实基础 位似图形
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 宝安区期中)如图,已知△A'B'C'与△ABC是以点O为位似中心的位似图形,位似比为3:5,下列说法错误的是( )
A.AC∥A'C'
B.S△A'B′C′:S△ABC=9:25
C.△BCO~△B'C'O
D.OB′:BB′=5:3
【考点】位似变换;平行线的判定.
【专题】图形的相似;几何直观;应用意识.
【答案】D
【分析】结合位似图形的定义、相似三角形的判定与性质逐项判断即可.
【解答】解:∵△A'B'C'与△ABC是以点O为位似中心的位似图形,位似比为3:5,
∴AC∥A'C',△A'B'C'∽△ABC,且相似比为3:5,
∴S△A'B'C':S△ABC=9:25.
故A,B选项正确,不符合题意;
∵△A'B'C'与△ABC是以点O为位似中心的位似图形,
∴BC∥B'C',
∴∠C'B'O=∠CBO,∠B'C'O=∠BCO,
∴△BCO~△B'C'O,
故C选项正确,不符合题意;
∵△A'B'C'与△ABC是以点O为位似中心的位似图形,位似比为3:5,
∴OB':OB=3:5,
∴OB′:BB′=3:2.
故D选项不正确,符合题意.
故选:D.
【点评】本题考查位似变换、平行线的判定,熟练掌握位似图形的定义、相似三角形的判定与性质是解答本题的关键.
2.(2024秋 大连期中)利用位似可以设计有立体感的美术字.如图,是某同学以点O为位似中心,设计“MATH”中字母“M”美术字的一种方法.若AB=5,A'B'=3,则的值为( )
A. B. C. D.
【考点】位似变换.
【专题】图形的相似;运算能力.
【答案】B
【分析】根据位似图形的性质知:,代入数值求解即可.
【解答】解:∵该图形是以点O为位似中心,
∴.
∵AB=5,A'B'=3,
∴.
故选:B.
【点评】本题考查的是位似变换.位似变换的两个图形相似.根据相似多边形对应边成比例.
3.(2024秋 铁西区期中)如图,△ABC与△DEF位似,点O是位似中心,若OA:AD=1:2,DF﹣AC=8,则DF+AC为( )
A.8 B.12 C.16 D.18
【考点】位似变换.
【专题】图形的相似;几何直观;推理能力.
【答案】C
【分析】首先根据题意可知,再结合位似图形的性质可得,结合DF﹣AC=8解得AC、DF的值,进而可得答案.
【解答】解:△ABC与△DEF位似,点O是位似中心,OA:AD=1:2,
∴,
∴,
∴DF=3AC,
∵DF﹣AC=8,
∴3AC﹣AC=2AC=8,
解得AC=4,
∴DF=3AC=12,
∴DF+AC=12+4=16.
故选:C.
【点评】本题主要考查了位似变换,熟练掌握位似图形的定义和性质是解题关键.
4.(2024秋 武强县期中)如图,△ABC与△DEF是位似图形,点O是位似中心.若OA=2AD,△ABC的周长为4,则△DEF的周长为( )
A.6 B.8 C.9 D.12
【考点】位似变换.
【专题】图形的相似;应用意识.
【答案】A
【分析】结合题意可得△ABC与△DEF的位似比为2:3,则△ABC与△DEF的周长比为2:3,进而可得答案.
【解答】解:∵OA=2AD,
∴OA:OD=2:3.
∵△ABC与△DEF是位似图形,点O是位似中心,
∴△ABC与△DEF的位似比为2:3,
∴△ABC与△DEF的周长比为2:3.
∵△ABC的周长为4,
∴△DEF的周长为6.
故选:A.
【点评】本题考查位似变换,熟练掌握位似的性质是解答本题的关键.
5.(2024秋 饶阳县期中)如图,△ABC与△A′B′C′位似,点O为位似中心,且点O在边AA′上.若AA′=3OA,BC=5,则B′C′的长为( )
A.5 B.10 C.15 D.20
【考点】位似变换.
【专题】图形的相似;推理能力.
【答案】B
【分析】根据位似图形的定义得到AC∥A′C′,得到△AOC∽△A′OC′,根据相似三角形的性质求出,进而求出,计算即可.
【解答】解:∵AA′=3OA,
∴OA:OA′=1:2,
∵△ABC与△A′B′C′位似,点O为位似中心,
∴AC∥A′C′,
∴△AOC∽△A′OC′,
∴,
∴,
∵BC=5,
∴B′C′=10,
故选:B.
【点评】本题考查的是位似变换,掌握位似图形的定义、相似三角形的性质是解题的关键.
二.填空题(共5小题)
6.(2024秋 长春期中)如图,以点A为位似中心的四边形ABCD和四边形AB′C′D′面积比为9:4,若AB=6,则AB′的长为 4 .
【考点】位似变换.
【专题】图形的相似;几何直观;应用意识.
【答案】4.
【分析】由题意得四边形ABCD与四边形AB′C′D′的相似比为3:2,即AB:AB'=3:2,进而可得答案.
【解答】解:∵以点A为位似中心的四边形ABCD和四边形AB′C′D′面积比为9:4,
∴四边形ABCD与四边形AB′C′D′的相似比为3:2,
∴AB:AB'=3:2,
∵AB=6,
∴AB′=4.
故答案为:4.
【点评】本题考查位似变换,熟练掌握位似的性质是解答本题的关键.
7.(2024秋 农安县期中)按下列方法,将△ABC的三边缩小为原来的,如图所示,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F,连接DE,EF,FD得到△DEF,则下列说法正确的序号有 ①②③ .
①△ABC与△DEF是位似图形;
②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长之比为2:1;
④△ABC与△DEF的面积之比为2:1.
【考点】位似变换.
【专题】图形的相似;推理能力.
【答案】①②③.
【分析】根据位似变换的定义和性质判断即可.
【解答】解:由题意可知:△ABC与△DEF是位似图形,故①说法正确;
△ABC与△DEF是相似图形,故②说法正确;
△ABC与△DEF的周长之比为2:1,故③说法正确;
△ABC与△DEF的面积之比为4:1,故④说法错误;
故答案为:①②③.
【点评】本题考查的是位似变换,位似是相似的特殊形式,位似比等于相似比,其对应的面积比等于相似比的平方.
8.(2024春 河口区期末)如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′=2:3,则四边形ABCD与四边形A′B′C′D′的面积比为 4:9 .
【考点】位似变换.
【专题】图形的相似;几何直观;推理能力.
【答案】4:9.
【分析】根据位似图形的性质和OA:OA′=2:3得到四边形ABCD和A′B′C′D′的相似比为2:3,即可得到答案.
【解答】解:∵四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,且OA:OA′=2:3,
∴四边形ABCD和A′B′C′D′的相似比为2:3,
∴四边形与四边形的面积比为4:9.
故答案为4:9.
【点评】此题考查了位似变换,掌握位似图形与相似图形的关系、相似多边形的性质是解题的关键.
9.(2024 久治县二模)如图,以点A为位似中心,把△ABC按相似比3:1放大得到△ADE,连接CD.若△ABC的面积为6,则△CDE的面积为 36 .
【考点】位似变换.
【专题】图形的相似;运算能力.
【答案】36.
【分析】根据位似变换的性质及三角形的面积公式求解.
【解答】解:∵△ABC按相似比3:1放大得到△ADE,
∴△ABC与△ADE的面积比为9:1,AB:DB=1:2,
∴△ADE的面积为54,△BDC的面积为12,
∴△CDE的面积为:54﹣6﹣12=36,
故答案为:36.
【点评】本题考查了位似变换,掌握位似变换的性质及三角形的面积公式的解题的关键.
10.(2024 东港区校级二模)《墨子 天志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形ABCD的周长为4,以它的对角线的交点为位似中心,作它的位似图形A′B′C′D′,若A′B′:AB=2:1,则四边形A′B′C′D′的周长为 8 .
【考点】位似变换;正方形的性质.
【专题】图形的相似;运算能力;推理能力.
【答案】8.
【分析】利用“相似多边形的周长之比等于相似比”求得答案.
【解答】解:根据题意知,正方形ABCD∽正方形A'B'C'D',且相似比为:AB:A'B'=2:1,
∴正方形ABCD的周长:四边形A'B'C'D'的周长=AB:A'B'=2:1.
∵正方形ABCD的周长为4,
∴四边形A′B′C′D′的周长为8.
故答案为:8.
【点评】本题考查位似变换,相似多边形的性质,圆的周长等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
三.解答题(共5小题)
11.(2024秋 市南区校级期中)在如图的方格纸中,△OAB的顶点坐标分别为O(0,0)、A(﹣2,﹣1)、B(﹣1,﹣3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.
(1)在图中标出位似中心P的位置,并写出点P及点B的对应点B1的坐标;
(2)△OAB的内部一点M的坐标为(a,b),写出M在△OA2B2中的对应点M2的坐标.
【考点】作图﹣位似变换.
【专题】作图题;平移、旋转与对称;几何直观.
【答案】(1)画图见解答;点P的坐标为(﹣5,﹣1),点B1的坐标为(3,﹣5).
(2)点M2的坐标为(2a+5,2b+1).
【分析】(1)连接O1O,A1A,B1B,并分别延长相交于点P,则点P即为所求,由图可得答案.
(2)根据题意可得点M2的坐标为(2a+5,2b+1).
【解答】解:(1)如图,连接O1O,A1A,B1B,并分别延长相交于点P,
则点P即为所求.
由图可得,点P的坐标为(﹣5,﹣1),点B1的坐标为(3,﹣5).
(2)由题意得,点M2的坐标为(2a+5,2b+1).
【点评】本题考查作图﹣位似变换,熟练掌握位似的性质是解答本题的关键.
12.(2024秋 福田区校级期中)如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(1,﹣2)、B(4,﹣1),C(3,﹣3).
(1)画出将△ABC向左平移5个单位,再向上平移3个单位后的△A1B1C1;
(2)以原点O为位似中心,在位似中心的同侧画出△A1B1C1的一个位似△A2B2C2,使它与△A1B1C1的相似比为2:1;
(3)若△A1B1C1内部任意一点P1的坐标为(a,b),直接写出经过(2)的变化后点P1的对应点P2的坐标(用含a、b的代数式表示).
【考点】作图﹣位似变换;作图﹣平移变换.
【专题】作图题;平移、旋转与对称;图形的相似;几何直观.
【答案】(1)见解答;
(2)见解答;
(3)点P2的坐标为:(2a,2b).
【分析】(1)利用平移的性质得出对应点坐标位置进而得出答案;
(2)画出一个以点O为位似中心的△A2B2C2,使得△A2B2C2与△A1B1C1的相似比为2即可;
(3)根据相似比即可求得.
【解答】解:(1)如图所示,△A1B1C1为所求三角形.
(2)如图所示,△A2B2C2为所求角形.
(3)由题意可知△A2B2C2∽△A2B2C2,且相似比为2:1,
∴当点P1的坐标为(a,b)时,对应点P2的坐标为:(2a,2b).
【点评】本题考查了平移作图,画位似图形,数形结合是解题的关键.
13.(2024秋 碑林区校级期中)尺规作图:如图,在矩形ABCD中,M是BC边的中点,连接AM,在AM上求作一点P,使得△DPA∽△ABM.(不写作法,保留作图痕迹)
【考点】作图﹣相似变换;矩形的性质.
【专题】作图题;几何直观.
【答案】见解析.
【分析】过点D作DP⊥AM于P,则点P即为所求.
【解答】解:如图所示,点P即为所求.
【点评】本题考查了作图﹣相似变换,矩形的性质,正确地作出图形是解题的关键.
14.(2024秋 碑林区校级期中)如图,在平面直角坐标系中,△ABC的顶点均在网格格点上,且点A、B、C的坐标分别为A(3,0),B(4,2),C(2,4).
(1)以点O为位似中心,在第一象限画出△ABC的位似图形△A1B1C1,使△A1B1C1与△ABC的相似比为2:1;
(2)在(1)的条件下,求△A1B1C1的面积.
【考点】作图﹣位似变换.
【专题】作图题;图形的相似;几何直观;运算能力.
【答案】(1)见解答.
(2)12.
【分析】(1)根据位似的性质作图即可.
(2)利用割补法求三角形的面积即可.
【解答】解:(1)如图所示,△A1B1C1即为所求.
(2)△A1B1C1的面积为24﹣4﹣8=12.
【点评】本题考查作图﹣位似变换,熟练掌握位似的性质是解答本题的关键.
15.(2024秋 泰兴市期中)如图,在△ABC中,AB=6,AC=10,点D是AB的中点.请用无刻度直尺和圆规在AC边上作出点E,使△ADE∽△ACB,并求AE的长.
【考点】作图﹣相似变换.
【专题】图形的相似;尺规作图;几何直观;推理能力.
【答案】作图见解析,AE=1.8.
【分析】以C为圆心,DA为半径作弧与CB,CA相交,两交点确定线段a,以D为圆心,DA为半径作弧,以A为圆心,线段a为半径作弧,两弧交于一点,连接点D与交点并延长与CA相交,即为点E;由△ADE∽△ACB得到,代入数据即可求解AE.
【解答】解:作图如下;
∵△ADE∽△ACB,
∴,
∵AB=6,AC=10,点D是AB的中点,
∴AD=3,
∴,
解得:AE=1.8.
【点评】本题考查了作图﹣相似变换,熟练掌握作一个角等于已知角的方法是解答本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
