23.6图形与坐标(预习衔接.夯实基础.含解析)-2025-2026学年九年级上册数学华东师大版
文档属性
| 名称 | 23.6图形与坐标(预习衔接.夯实基础.含解析)-2025-2026学年九年级上册数学华东师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 339.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 21:18:33 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
预习衔接.夯实基础 图形与坐标
一.选择题(共5小题)
1.(2024秋 南海区期中)点A(5,﹣2)关于y轴对称的点坐标是( )
A.(﹣5,﹣2) B.(5,2) C.(﹣5,2) D.(﹣2,5)
2.(2024秋 市南区校级期中)如图,小石同学在正方形网格中确定点A的坐标为(﹣6,4),点B的坐标为(0,2),则点C的坐标为( )
A.(2,﹣2) B.(﹣2,﹣2) C.(﹣1,﹣1) D.(1,﹣1)
3.(2024 冷水滩区校级模拟)“在生活的舞台上,我们都是不屈不挠的拳击手,面对无尽的挑战,挥洒汗水,拼搏向前!”今年的春节档《热辣滚烫》展现了角色坚韧不拔的精神面貌,小明、小华、小亮三人也观看了此电影.如图是利用平面直角坐标系画出的影院内分布图,若分别以正东、正北方向为x轴、y轴的正方向,建立平面直角坐标系xOy,他们是这样描述自己的座位:
①小明:表示我座位的坐标为(﹣2,3);
②小华:在小明的座位向右走4个座位,再向上走2个座位,就可以找到我了;
③小亮:小旗帜所在的位置就是我的座位了.
则表示小华、小亮座位的坐标分别为( )
A.(2,5),(2,﹣1) B.(﹣4,5),(﹣4,0)
C.(4,2),(4,7) D.(2,5),(2,0)
4.(2024秋 深圳期中)老师写出第二象限的一点的坐标(﹣2,☆),小明不小心,把纵坐标给弄脏看不清了,则☆挡住的纵坐标可能是( )
A.﹣1 B.﹣2 C.0 D.2
5.(2024秋 宝安区期中)剪纸是中国古代最古老的民间艺术之一,其中蕴含着图形的变换.如图是一张蕴含着轴对称变换的蝴蝶剪纸,点A与点B对称,点C与点D对称,将其放置在直角坐标系中,点A,B,C的坐标分别为(2,0),(4,0),(0.5,4),则点D的坐标为( )
A.(3.5,4) B.(5.5,4) C.(5,4) D.(6,4)
二.填空题(共5小题)
6.(2024秋 九原区期中)如图,过点A的直线L∥x轴,点B在x轴的正半轴上,OC平分∠AOB交L于点C(2,4),则A的坐标是 .
7.(2024秋 金水区校级月考)已知点P的坐标(2﹣a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是 .
8.(2024秋 威海期末)如图,围棋棋盘放在某平面直角坐标系中,已知黑棋(甲)的坐标为(1,1),黑棋(乙)的坐标为(﹣1,﹣2),则白棋(甲)的坐标为 .
9.(2024秋 招远市期末)如图,在平面直角坐标系中,将线段AB绕点A按逆时针方向旋转90°后,得到线段A'B',则点B'的坐标为 .
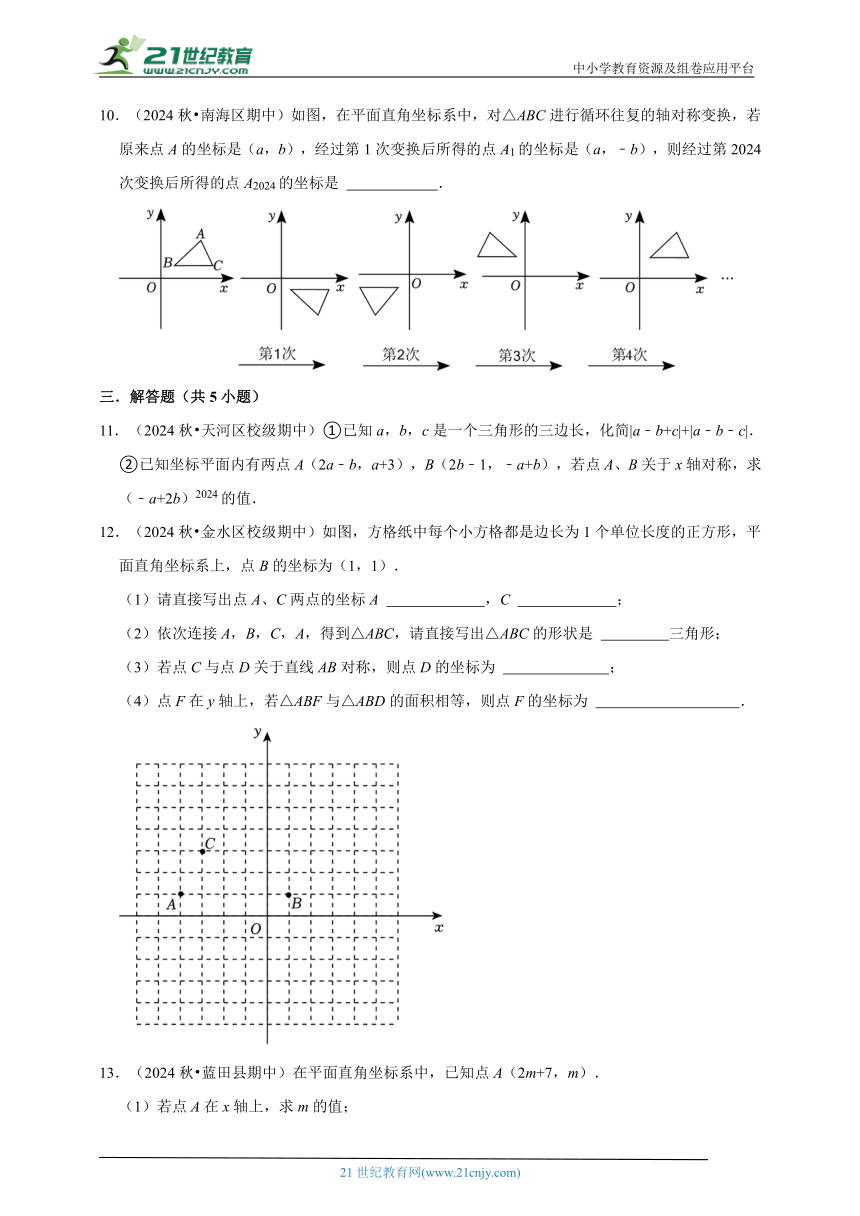
10.(2024秋 南海区期中)如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A的坐标是(a,b),经过第1次变换后所得的点A1的坐标是(a,﹣b),则经过第2024次变换后所得的点A2024的坐标是 .
三.解答题(共5小题)
11.(2024秋 天河区校级期中)①已知a,b,c是一个三角形的三边长,化简|a﹣b+c|+|a﹣b﹣c|.
②已知坐标平面内有两点A(2a﹣b,a+3),B(2b﹣1,﹣a+b),若点A、B关于x轴对称,求(﹣a+2b)2024的值.
12.(2024秋 金水区校级期中)如图,方格纸中每个小方格都是边长为1个单位长度的正方形,平面直角坐标系上,点B的坐标为(1,1).
(1)请直接写出点A、C两点的坐标A ,C ;
(2)依次连接A,B,C,A,得到△ABC,请直接写出△ABC的形状是 三角形;
(3)若点C与点D关于直线AB对称,则点D的坐标为 ;
(4)点F在y轴上,若△ABF与△ABD的面积相等,则点F的坐标为 .
13.(2024秋 蓝田县期中)在平面直角坐标系中,已知点A(2m+7,m).
(1)若点A在x轴上,求m的值;
(2)若点A在第四象限且到两坐标轴的距离之和为4,求m的值.
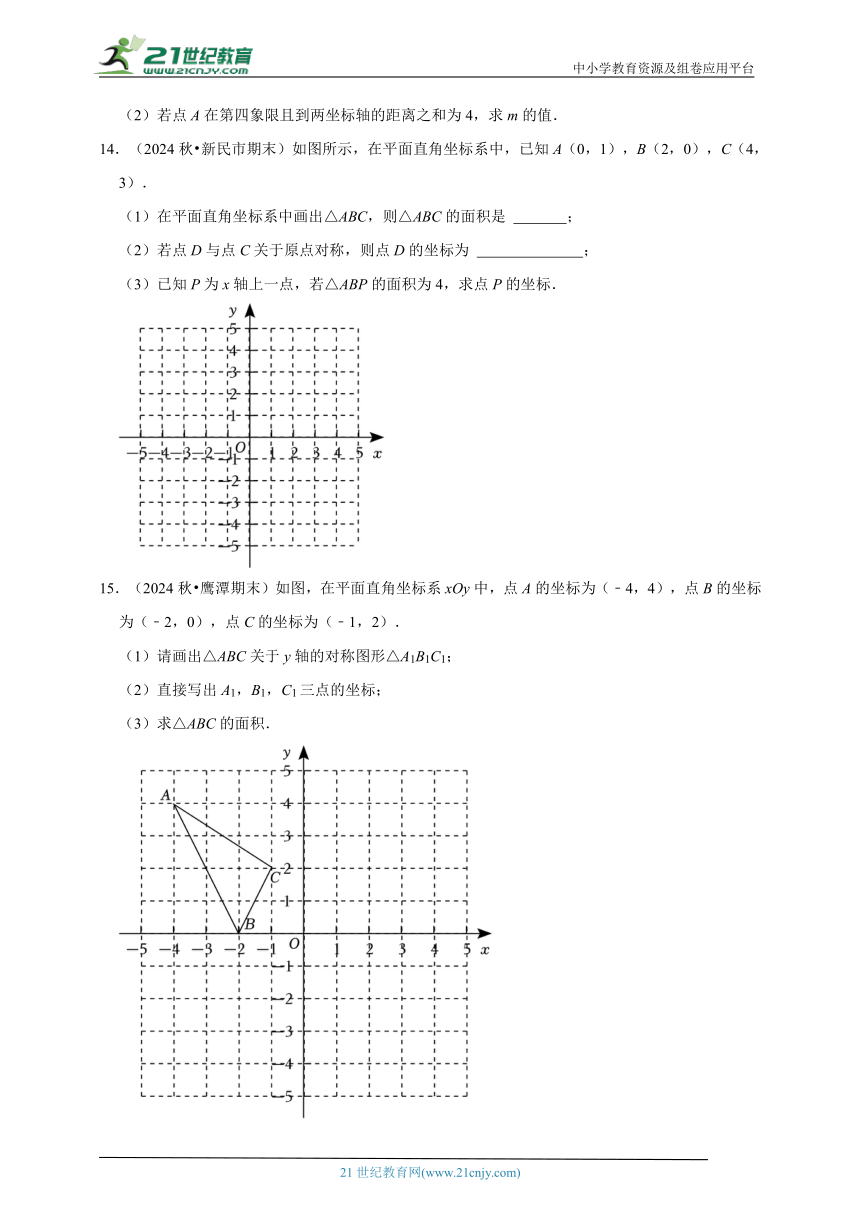
14.(2024秋 新民市期末)如图所示,在平面直角坐标系中,已知A(0,1),B(2,0),C(4,3).
(1)在平面直角坐标系中画出△ABC,则△ABC的面积是 ;
(2)若点D与点C关于原点对称,则点D的坐标为 ;
(3)已知P为x轴上一点,若△ABP的面积为4,求点P的坐标.
15.(2024秋 鹰潭期末)如图,在平面直角坐标系xOy中,点A的坐标为(﹣4,4),点B的坐标为(﹣2,0),点C的坐标为(﹣1,2).
(1)请画出△ABC关于y轴的对称图形△A1B1C1;
(2)直接写出A1,B1,C1三点的坐标;
(3)求△ABC的面积.
预习衔接.夯实基础 图形与坐标
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 南海区期中)点A(5,﹣2)关于y轴对称的点坐标是( )
A.(﹣5,﹣2) B.(5,2) C.(﹣5,2) D.(﹣2,5)
【考点】关于x轴、y轴对称的点的坐标.
【专题】平面直角坐标系;运算能力.
【答案】A
【分析】根据关于y轴对称的点,横坐标互为相反数,纵坐标相同即可求解.
【解答】解:点A(5,﹣2)关于y轴对称的点坐标是(﹣5,﹣2),
故选:A.
【点评】本题考查了关于y轴对称的点的坐标特征,掌握关于y轴对称的点的坐标特征是解题的关键.
2.(2024秋 市南区校级期中)如图,小石同学在正方形网格中确定点A的坐标为(﹣6,4),点B的坐标为(0,2),则点C的坐标为( )
A.(2,﹣2) B.(﹣2,﹣2) C.(﹣1,﹣1) D.(1,﹣1)
【考点】点的坐标.
【专题】平面直角坐标系;几何直观.
【答案】B
【分析】直接利用已知点坐标确定平面直角坐标系,进而得出答案.
【解答】解:如图所示:点C的坐标为(﹣2,﹣2).
故选:B.
【点评】此题主要考查了点的坐标,正确得出原点位置是解题的关键.
3.(2024 冷水滩区校级模拟)“在生活的舞台上,我们都是不屈不挠的拳击手,面对无尽的挑战,挥洒汗水,拼搏向前!”今年的春节档《热辣滚烫》展现了角色坚韧不拔的精神面貌,小明、小华、小亮三人也观看了此电影.如图是利用平面直角坐标系画出的影院内分布图,若分别以正东、正北方向为x轴、y轴的正方向,建立平面直角坐标系xOy,他们是这样描述自己的座位:
①小明:表示我座位的坐标为(﹣2,3);
②小华:在小明的座位向右走4个座位,再向上走2个座位,就可以找到我了;
③小亮:小旗帜所在的位置就是我的座位了.
则表示小华、小亮座位的坐标分别为( )
A.(2,5),(2,﹣1) B.(﹣4,5),(﹣4,0)
C.(4,2),(4,7) D.(2,5),(2,0)
【考点】坐标确定位置.
【专题】平面直角坐标系;几何直观.
【答案】D
【分析】直接利用以正东、正北方向为x轴、y轴的正方向,建立平面直角坐标系,进而分别分析得出答案.
【解答】解:建立平面直角坐标系如图,
∵小明座位的坐标为(﹣2,3),
又∵小华座位的坐标:在小明的座位向右走4个座位,再向上走2个座位,
∴小华座位的坐标为(2,5),
∵小旗帜位置的坐标为(2,0),
∴小亮座位的坐标为(2,0),
故选:D.
【点评】本题考查坐标确定位置,正确理解横纵坐标的意义是解题关键.
4.(2024秋 深圳期中)老师写出第二象限的一点的坐标(﹣2,☆),小明不小心,把纵坐标给弄脏看不清了,则☆挡住的纵坐标可能是( )
A.﹣1 B.﹣2 C.0 D.2
【考点】点的坐标.
【专题】平面直角坐标系;符号意识.
【答案】D
【分析】四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).根据平面直角坐标系内第二象限点的坐标的特点解答即可.
【解答】解:∵第二象限的一点的坐标(﹣2,☆),
∴☆>0,
只有选项D符合题意.
故选:D.
【点评】本题考查点的坐标.熟记各象限内点的坐标的符号是解决的关键.
5.(2024秋 宝安区期中)剪纸是中国古代最古老的民间艺术之一,其中蕴含着图形的变换.如图是一张蕴含着轴对称变换的蝴蝶剪纸,点A与点B对称,点C与点D对称,将其放置在直角坐标系中,点A,B,C的坐标分别为(2,0),(4,0),(0.5,4),则点D的坐标为( )
A.(3.5,4) B.(5.5,4) C.(5,4) D.(6,4)
【考点】坐标与图形变化﹣对称;坐标确定位置.
【专题】平移、旋转与对称;运算能力.
【答案】B
【分析】由点A与点B对称,求得对称轴为直线x=3,再根据点C与点D对称,即可求解.
【解答】解:∵(2,0)与(4,0)对称,
∴对称轴为直线,
∵C(0.5,4)与点D关于直线x=3对称,
∴点D的坐标为(5.5,4).
故选:B.
【点评】本题考查了轴对称的性质,熟练掌握对称点到对称轴的距离相等是解答本题的关键.
二.填空题(共5小题)
6.(2024秋 九原区期中)如图,过点A的直线L∥x轴,点B在x轴的正半轴上,OC平分∠AOB交L于点C(2,4),则A的坐标是 (﹣3,4) .
【考点】坐标与图形性质;角平分线的定义;平行线的性质;勾股定理.
【专题】平面直角坐标系;几何直观.
【答案】(﹣3,4).
【分析】先根据点C坐标得出点A的纵坐标,再结合平行线的性质及勾股定理即可解决问题.
【解答】解:令直线L与y轴的交点为M,
∵OC平分∠AOB,
∴∠AOC=∠BOC.
∵直线L∥x轴,
∴∠ACO=∠BOC,
∴∠AOC=∠BCO,
∴AO=AC.
∵点C的坐标为(2,4),
∴MC=2,OM=4,
∴AO=AC=AM+2.
在Rt△AMO中,
AO2=AM2+MO2,
∴(AM+2)2=AM2+42,
解得AM=3,
又∵直线L∥x轴,
∴点A的坐标为(﹣3,4).
故答案为:(﹣3,4).
【点评】本题主要考查了坐标与图形性质、平行线的性质、角平分线的定义及勾股定理,熟知平行线的性质、角平分线的定义及勾股定理是解题的关键.
7.(2024秋 金水区校级月考)已知点P的坐标(2﹣a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是 (3,3)或(6,﹣6) .
【考点】点的坐标.
【答案】见试题解答内容
【分析】点P到两坐标轴的距离相等就是横纵坐标相等或互为相反数,就可以得到方程求出a的值,从而求出点的坐标.
【解答】解:∵点P到两坐标轴的距离相等就是横纵坐标相等或互为相反数,
∴分以下两种情考虑:
①横纵坐标相等时,即当2﹣a=3a+6时,解得a=﹣1,
∴点P的坐标是(3,3);
②横纵坐标互为相反数时,即当(2﹣a)+(3a+6)=0时,解得a=﹣4,
∴点P的坐标是(6,﹣6).
故答案为(3,3)或(6,﹣6).
【点评】因为这个点到两坐标轴的距离相等,即到坐标轴形成的角的两边距离相等,所以这个点一定在各象限的角平分线上.
8.(2024秋 威海期末)如图,围棋棋盘放在某平面直角坐标系中,已知黑棋(甲)的坐标为(1,1),黑棋(乙)的坐标为(﹣1,﹣2),则白棋(甲)的坐标为 (﹣3,2) .
【考点】坐标确定位置.
【专题】平面直角坐标系;几何直观.
【答案】(﹣3,2).
【分析】先利用黑棋(甲)的坐标为(1,1)画出直角坐标系,然后可写出白棋(甲)的坐标.
【解答】解:如图,
白棋(甲)的坐标是(﹣3,2).
故答案为:(﹣3,2).
【点评】本题考查了坐标确定位置:平面内的点与有序实数对一一对应;记住平面内特殊位置的点的坐标特征.
9.(2024秋 招远市期末)如图,在平面直角坐标系中,将线段AB绕点A按逆时针方向旋转90°后,得到线段A'B',则点B'的坐标为 (4,1) .
【考点】坐标与图形变化﹣旋转.
【专题】平移、旋转与对称;推理能力.
【答案】(4,1).
【分析】根据题意画出旋转后的图形,借助于全等三角形即可解决问题.
【解答】解:将线段AB绕点A按逆时针方向旋转90°如图所示,
过点A作y轴的平行线分别与过点B作x轴的平行线和过点B′作x轴的平行线相交于点M,N,
∵∠BAB′=90°,
∴∠BAM+∠B′AN=90°,
又∵∠BAM+∠ABM=90°,
∴∠ABM=∠B′AN.
在△ABM和△B′AN中,
,
∴△ABM≌△B′AN(AAS),
∴B′N=AM=1,AN=BM=3,
∴点B′的坐标为(4,1).
故答案为:(4,1).
【点评】本题考查坐标与图形变化﹣旋转,熟知图形旋转的性质是解题的关键.
10.(2024秋 南海区期中)如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A的坐标是(a,b),经过第1次变换后所得的点A1的坐标是(a,﹣b),则经过第2024次变换后所得的点A2024的坐标是 (a,b) .
【考点】坐标与图形变化﹣对称;规律型:点的坐标;关于x轴、y轴对称的点的坐标.
【专题】规律型;平移、旋转与对称;推理能力.
【答案】(a,b).
【分析】图观察图形可知每四次对称为一个循环组依次循环,用2024除以4,然后根据商的情况确定出变换后的点A所在的象限,然后解答即可.
【解答】解:点A第一次关于x轴对称后在第四象限,
点A第二次关于y轴对称后在第三象限,
点A第三次关于x轴对称后在第二象限,
点A第四次关于y轴对称后在第一象限,
即点A回到原始位置,
所以,每四次对称为一个循环组依次循环,
∵2024÷4=506,
∴经过第2024次变换后所得的A点与第四次变换的位置相同,在第一象限,即回到原始位置,
坐标为(a,b).
故答案为:(a,b).
【点评】本题考查了轴对称的性质,点的坐标变换规律,读懂题目信息,观察出每四次对称为一个循环组依次循环是解题的关键,也是本题的难点.
三.解答题(共5小题)
11.(2024秋 天河区校级期中)①已知a,b,c是一个三角形的三边长,化简|a﹣b+c|+|a﹣b﹣c|.
②已知坐标平面内有两点A(2a﹣b,a+3),B(2b﹣1,﹣a+b),若点A、B关于x轴对称,求(﹣a+2b)2024的值.
【考点】关于x轴、y轴对称的点的坐标;绝对值;三角形三边关系.
【专题】平面直角坐标系;运算能力.
【答案】①2c;②1.
【分析】①根据三角形三边关系得到a﹣b﹣c<0,a﹣b+c>0,再去绝对值,合并同类项即可求解.
②根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”列方程组求出a、b的值,然后代入代数式进行计算即可得解.
【解答】解:①a﹣b﹣c=a﹣(b+c)<0,a﹣b+c=a+c﹣b>0,
|a﹣b+c|+|a﹣b﹣c|=a﹣b+c﹣a+b+c=2c.
②∵点A、B关于x轴对称,
∴,
∴,
∴(﹣a+2b)2024=(5﹣6)2024=1.
【点评】本题考查了解二元一次方程组,轴对称的性质,三角形三边关系,绝对值的性质,关于x、y轴对称的点的坐标特征:点P(x,y)关于x轴的对称点P′的坐标是(x,﹣y).点P(x,y)关于y轴的对称点P′的坐标是(﹣x,y),正确掌握相关性质内容是解题的关键.
12.(2024秋 金水区校级期中)如图,方格纸中每个小方格都是边长为1个单位长度的正方形,平面直角坐标系上,点B的坐标为(1,1).
(1)请直接写出点A、C两点的坐标A (﹣4,1) ,C (﹣3,3) ;
(2)依次连接A,B,C,A,得到△ABC,请直接写出△ABC的形状是 直角 三角形;
(3)若点C与点D关于直线AB对称,则点D的坐标为 (﹣3,﹣1) ;
(4)点F在y轴上,若△ABF与△ABD的面积相等,则点F的坐标为 (0,3)或(0,﹣1) .
【考点】坐标与图形变化﹣对称;勾股定理;勾股定理的逆定理.
【专题】平面直角坐标系;平移、旋转与对称;几何直观.
【答案】(1)(﹣4,1),(﹣3,3);
(2)直角;
(3)(﹣3,﹣1);
(4)(0,3)或(0,﹣1).
【分析】(1)根据所给平面直角坐标系,写出点A和点C的坐标即可解决问题.
(2)根据所给网格,利用勾股定理及其逆定理即可解决问题.
(3)根据轴对称的性质即可解决问题.
(4)根据△ABF与△ABD的面积相等,得出点F到AB的距离与点D到AB的距离相等,据此可解决问题.
【解答】解:(1)由所给平面直角坐标系可知,
点A坐标为(﹣4,1),点C坐标为(﹣3,3).
故答案为:(﹣4,1),(﹣3,3).
(2)如图所示,
由勾股定理得,
AC2=12+22=5,BC2=22+42=20,5≠20,
又因为AB2=52=25,
所以AC2+BC2=AB2,
所以△ABC是直角三角形,
故答案为:直角.
(3)因为3﹣1=2,1﹣2=﹣1,
所以点C关于直线AB的对称点D的坐标为(﹣3,﹣1).
故答案为:(﹣3,﹣1).
(4)因为△ABF与△ABD的面积相等,
所以点F到AB的距离与点D到AB的距离相等.
又因为1﹣(﹣1)=2,
则点F到AB的距离为2,
所以1+2=3,1﹣2=﹣1,
所以点F的坐标为(0,3)或(0,﹣1).
故答案为:(0,3)或(0,﹣1).
【点评】本题主要考查了坐标与图形变化﹣对称、勾股定理及勾股定理的逆定理,熟知轴对称的性质及勾股定理与其逆定理是解题的关键.
13.(2024秋 蓝田县期中)在平面直角坐标系中,已知点A(2m+7,m).
(1)若点A在x轴上,求m的值;
(2)若点A在第四象限且到两坐标轴的距离之和为4,求m的值.
【考点】点的坐标.
【专题】平面直角坐标系;运算能力.
【答案】(1)m=0;
(2)m=﹣3.
【分析】(1)根据x轴上的点的纵坐标为0可得答案;
(2)根据A到两坐标轴的距离之和为4列出绝对值方程,再根据A在第四象限去绝对值解方程即可.
【解答】解:(1)∵点A在x轴上,
∴m=0;
(2)∵点A(2m+7,m)在第四象限且到两坐标轴的距离之和为4,
∴A的横坐标为正,纵坐标为负,|2m+7|+|m|=4,
∴2m+7﹣m=4,
∴m=﹣3.
【点评】本题考查点的坐标,关键是掌握坐标轴上的点的坐标特征,点到坐标轴的距离.
14.(2024秋 新民市期末)如图所示,在平面直角坐标系中,已知A(0,1),B(2,0),C(4,3).
(1)在平面直角坐标系中画出△ABC,则△ABC的面积是 4 ;
(2)若点D与点C关于原点对称,则点D的坐标为 (﹣4,﹣3) ;
(3)已知P为x轴上一点,若△ABP的面积为4,求点P的坐标.
【考点】关于原点对称的点的坐标;三角形的面积.
【专题】平面直角坐标系;运算能力.
【答案】(1)4;
(2)(﹣4,﹣3);
(3)(10,0)或(﹣6,0).
【分析】(1)直接利用△ABC所在矩形面积减去周围三角形面积进而得出答案;
(2)利用关于原点对称点的性质得出答案;
(3)利用三角形面积求法得出符合题意的答案.
【解答】解:(1)如图所示:△ABC的面积是:3×4;
故答案为:4;
(2)点D与点C关于原点对称,则点D的坐标为:(﹣4,﹣3);
故答案为:(﹣4,﹣3);
(3)∵P为x轴上一点,△ABP的面积为4,
∴BP=8,
∴点P的横坐标为:2+8=10或2﹣8=﹣6,
故P点坐标为:(10,0)或(﹣6,0).
【点评】此题主要考查了三角形面积求法以及关于y轴对称点的性质,正确得出对应点位置是解题关键.
15.(2024秋 鹰潭期末)如图,在平面直角坐标系xOy中,点A的坐标为(﹣4,4),点B的坐标为(﹣2,0),点C的坐标为(﹣1,2).
(1)请画出△ABC关于y轴的对称图形△A1B1C1;
(2)直接写出A1,B1,C1三点的坐标;
(3)求△ABC的面积.
【考点】关于x轴、y轴对称的点的坐标;三角形的面积.
【专题】作图题;平面直角坐标系;几何直观.
【答案】见试题解答内容
【分析】(1)关于y轴对称的点,横坐标互为相反数,纵坐标不变;根据轴对称的性质作图即可;
(2)由(1)可得答案;
(3)利用割补法求三角形的面积即可.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)由(1)得A1(4,4),B1(2,0),C1(1,2);
(3)△ABC的面积为3×44.
【点评】本题考查作图﹣轴对称变换、三角形的面积,熟练掌握轴对称的性质是解答本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.夯实基础 图形与坐标
一.选择题(共5小题)
1.(2024秋 南海区期中)点A(5,﹣2)关于y轴对称的点坐标是( )
A.(﹣5,﹣2) B.(5,2) C.(﹣5,2) D.(﹣2,5)
2.(2024秋 市南区校级期中)如图,小石同学在正方形网格中确定点A的坐标为(﹣6,4),点B的坐标为(0,2),则点C的坐标为( )
A.(2,﹣2) B.(﹣2,﹣2) C.(﹣1,﹣1) D.(1,﹣1)
3.(2024 冷水滩区校级模拟)“在生活的舞台上,我们都是不屈不挠的拳击手,面对无尽的挑战,挥洒汗水,拼搏向前!”今年的春节档《热辣滚烫》展现了角色坚韧不拔的精神面貌,小明、小华、小亮三人也观看了此电影.如图是利用平面直角坐标系画出的影院内分布图,若分别以正东、正北方向为x轴、y轴的正方向,建立平面直角坐标系xOy,他们是这样描述自己的座位:
①小明:表示我座位的坐标为(﹣2,3);
②小华:在小明的座位向右走4个座位,再向上走2个座位,就可以找到我了;
③小亮:小旗帜所在的位置就是我的座位了.
则表示小华、小亮座位的坐标分别为( )
A.(2,5),(2,﹣1) B.(﹣4,5),(﹣4,0)
C.(4,2),(4,7) D.(2,5),(2,0)
4.(2024秋 深圳期中)老师写出第二象限的一点的坐标(﹣2,☆),小明不小心,把纵坐标给弄脏看不清了,则☆挡住的纵坐标可能是( )
A.﹣1 B.﹣2 C.0 D.2
5.(2024秋 宝安区期中)剪纸是中国古代最古老的民间艺术之一,其中蕴含着图形的变换.如图是一张蕴含着轴对称变换的蝴蝶剪纸,点A与点B对称,点C与点D对称,将其放置在直角坐标系中,点A,B,C的坐标分别为(2,0),(4,0),(0.5,4),则点D的坐标为( )
A.(3.5,4) B.(5.5,4) C.(5,4) D.(6,4)
二.填空题(共5小题)
6.(2024秋 九原区期中)如图,过点A的直线L∥x轴,点B在x轴的正半轴上,OC平分∠AOB交L于点C(2,4),则A的坐标是 .
7.(2024秋 金水区校级月考)已知点P的坐标(2﹣a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是 .
8.(2024秋 威海期末)如图,围棋棋盘放在某平面直角坐标系中,已知黑棋(甲)的坐标为(1,1),黑棋(乙)的坐标为(﹣1,﹣2),则白棋(甲)的坐标为 .
9.(2024秋 招远市期末)如图,在平面直角坐标系中,将线段AB绕点A按逆时针方向旋转90°后,得到线段A'B',则点B'的坐标为 .
10.(2024秋 南海区期中)如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A的坐标是(a,b),经过第1次变换后所得的点A1的坐标是(a,﹣b),则经过第2024次变换后所得的点A2024的坐标是 .
三.解答题(共5小题)
11.(2024秋 天河区校级期中)①已知a,b,c是一个三角形的三边长,化简|a﹣b+c|+|a﹣b﹣c|.
②已知坐标平面内有两点A(2a﹣b,a+3),B(2b﹣1,﹣a+b),若点A、B关于x轴对称,求(﹣a+2b)2024的值.
12.(2024秋 金水区校级期中)如图,方格纸中每个小方格都是边长为1个单位长度的正方形,平面直角坐标系上,点B的坐标为(1,1).
(1)请直接写出点A、C两点的坐标A ,C ;
(2)依次连接A,B,C,A,得到△ABC,请直接写出△ABC的形状是 三角形;
(3)若点C与点D关于直线AB对称,则点D的坐标为 ;
(4)点F在y轴上,若△ABF与△ABD的面积相等,则点F的坐标为 .
13.(2024秋 蓝田县期中)在平面直角坐标系中,已知点A(2m+7,m).
(1)若点A在x轴上,求m的值;
(2)若点A在第四象限且到两坐标轴的距离之和为4,求m的值.
14.(2024秋 新民市期末)如图所示,在平面直角坐标系中,已知A(0,1),B(2,0),C(4,3).
(1)在平面直角坐标系中画出△ABC,则△ABC的面积是 ;
(2)若点D与点C关于原点对称,则点D的坐标为 ;
(3)已知P为x轴上一点,若△ABP的面积为4,求点P的坐标.
15.(2024秋 鹰潭期末)如图,在平面直角坐标系xOy中,点A的坐标为(﹣4,4),点B的坐标为(﹣2,0),点C的坐标为(﹣1,2).
(1)请画出△ABC关于y轴的对称图形△A1B1C1;
(2)直接写出A1,B1,C1三点的坐标;
(3)求△ABC的面积.
预习衔接.夯实基础 图形与坐标
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 南海区期中)点A(5,﹣2)关于y轴对称的点坐标是( )
A.(﹣5,﹣2) B.(5,2) C.(﹣5,2) D.(﹣2,5)
【考点】关于x轴、y轴对称的点的坐标.
【专题】平面直角坐标系;运算能力.
【答案】A
【分析】根据关于y轴对称的点,横坐标互为相反数,纵坐标相同即可求解.
【解答】解:点A(5,﹣2)关于y轴对称的点坐标是(﹣5,﹣2),
故选:A.
【点评】本题考查了关于y轴对称的点的坐标特征,掌握关于y轴对称的点的坐标特征是解题的关键.
2.(2024秋 市南区校级期中)如图,小石同学在正方形网格中确定点A的坐标为(﹣6,4),点B的坐标为(0,2),则点C的坐标为( )
A.(2,﹣2) B.(﹣2,﹣2) C.(﹣1,﹣1) D.(1,﹣1)
【考点】点的坐标.
【专题】平面直角坐标系;几何直观.
【答案】B
【分析】直接利用已知点坐标确定平面直角坐标系,进而得出答案.
【解答】解:如图所示:点C的坐标为(﹣2,﹣2).
故选:B.
【点评】此题主要考查了点的坐标,正确得出原点位置是解题的关键.
3.(2024 冷水滩区校级模拟)“在生活的舞台上,我们都是不屈不挠的拳击手,面对无尽的挑战,挥洒汗水,拼搏向前!”今年的春节档《热辣滚烫》展现了角色坚韧不拔的精神面貌,小明、小华、小亮三人也观看了此电影.如图是利用平面直角坐标系画出的影院内分布图,若分别以正东、正北方向为x轴、y轴的正方向,建立平面直角坐标系xOy,他们是这样描述自己的座位:
①小明:表示我座位的坐标为(﹣2,3);
②小华:在小明的座位向右走4个座位,再向上走2个座位,就可以找到我了;
③小亮:小旗帜所在的位置就是我的座位了.
则表示小华、小亮座位的坐标分别为( )
A.(2,5),(2,﹣1) B.(﹣4,5),(﹣4,0)
C.(4,2),(4,7) D.(2,5),(2,0)
【考点】坐标确定位置.
【专题】平面直角坐标系;几何直观.
【答案】D
【分析】直接利用以正东、正北方向为x轴、y轴的正方向,建立平面直角坐标系,进而分别分析得出答案.
【解答】解:建立平面直角坐标系如图,
∵小明座位的坐标为(﹣2,3),
又∵小华座位的坐标:在小明的座位向右走4个座位,再向上走2个座位,
∴小华座位的坐标为(2,5),
∵小旗帜位置的坐标为(2,0),
∴小亮座位的坐标为(2,0),
故选:D.
【点评】本题考查坐标确定位置,正确理解横纵坐标的意义是解题关键.
4.(2024秋 深圳期中)老师写出第二象限的一点的坐标(﹣2,☆),小明不小心,把纵坐标给弄脏看不清了,则☆挡住的纵坐标可能是( )
A.﹣1 B.﹣2 C.0 D.2
【考点】点的坐标.
【专题】平面直角坐标系;符号意识.
【答案】D
【分析】四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).根据平面直角坐标系内第二象限点的坐标的特点解答即可.
【解答】解:∵第二象限的一点的坐标(﹣2,☆),
∴☆>0,
只有选项D符合题意.
故选:D.
【点评】本题考查点的坐标.熟记各象限内点的坐标的符号是解决的关键.
5.(2024秋 宝安区期中)剪纸是中国古代最古老的民间艺术之一,其中蕴含着图形的变换.如图是一张蕴含着轴对称变换的蝴蝶剪纸,点A与点B对称,点C与点D对称,将其放置在直角坐标系中,点A,B,C的坐标分别为(2,0),(4,0),(0.5,4),则点D的坐标为( )
A.(3.5,4) B.(5.5,4) C.(5,4) D.(6,4)
【考点】坐标与图形变化﹣对称;坐标确定位置.
【专题】平移、旋转与对称;运算能力.
【答案】B
【分析】由点A与点B对称,求得对称轴为直线x=3,再根据点C与点D对称,即可求解.
【解答】解:∵(2,0)与(4,0)对称,
∴对称轴为直线,
∵C(0.5,4)与点D关于直线x=3对称,
∴点D的坐标为(5.5,4).
故选:B.
【点评】本题考查了轴对称的性质,熟练掌握对称点到对称轴的距离相等是解答本题的关键.
二.填空题(共5小题)
6.(2024秋 九原区期中)如图,过点A的直线L∥x轴,点B在x轴的正半轴上,OC平分∠AOB交L于点C(2,4),则A的坐标是 (﹣3,4) .
【考点】坐标与图形性质;角平分线的定义;平行线的性质;勾股定理.
【专题】平面直角坐标系;几何直观.
【答案】(﹣3,4).
【分析】先根据点C坐标得出点A的纵坐标,再结合平行线的性质及勾股定理即可解决问题.
【解答】解:令直线L与y轴的交点为M,
∵OC平分∠AOB,
∴∠AOC=∠BOC.
∵直线L∥x轴,
∴∠ACO=∠BOC,
∴∠AOC=∠BCO,
∴AO=AC.
∵点C的坐标为(2,4),
∴MC=2,OM=4,
∴AO=AC=AM+2.
在Rt△AMO中,
AO2=AM2+MO2,
∴(AM+2)2=AM2+42,
解得AM=3,
又∵直线L∥x轴,
∴点A的坐标为(﹣3,4).
故答案为:(﹣3,4).
【点评】本题主要考查了坐标与图形性质、平行线的性质、角平分线的定义及勾股定理,熟知平行线的性质、角平分线的定义及勾股定理是解题的关键.
7.(2024秋 金水区校级月考)已知点P的坐标(2﹣a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是 (3,3)或(6,﹣6) .
【考点】点的坐标.
【答案】见试题解答内容
【分析】点P到两坐标轴的距离相等就是横纵坐标相等或互为相反数,就可以得到方程求出a的值,从而求出点的坐标.
【解答】解:∵点P到两坐标轴的距离相等就是横纵坐标相等或互为相反数,
∴分以下两种情考虑:
①横纵坐标相等时,即当2﹣a=3a+6时,解得a=﹣1,
∴点P的坐标是(3,3);
②横纵坐标互为相反数时,即当(2﹣a)+(3a+6)=0时,解得a=﹣4,
∴点P的坐标是(6,﹣6).
故答案为(3,3)或(6,﹣6).
【点评】因为这个点到两坐标轴的距离相等,即到坐标轴形成的角的两边距离相等,所以这个点一定在各象限的角平分线上.
8.(2024秋 威海期末)如图,围棋棋盘放在某平面直角坐标系中,已知黑棋(甲)的坐标为(1,1),黑棋(乙)的坐标为(﹣1,﹣2),则白棋(甲)的坐标为 (﹣3,2) .
【考点】坐标确定位置.
【专题】平面直角坐标系;几何直观.
【答案】(﹣3,2).
【分析】先利用黑棋(甲)的坐标为(1,1)画出直角坐标系,然后可写出白棋(甲)的坐标.
【解答】解:如图,
白棋(甲)的坐标是(﹣3,2).
故答案为:(﹣3,2).
【点评】本题考查了坐标确定位置:平面内的点与有序实数对一一对应;记住平面内特殊位置的点的坐标特征.
9.(2024秋 招远市期末)如图,在平面直角坐标系中,将线段AB绕点A按逆时针方向旋转90°后,得到线段A'B',则点B'的坐标为 (4,1) .
【考点】坐标与图形变化﹣旋转.
【专题】平移、旋转与对称;推理能力.
【答案】(4,1).
【分析】根据题意画出旋转后的图形,借助于全等三角形即可解决问题.
【解答】解:将线段AB绕点A按逆时针方向旋转90°如图所示,
过点A作y轴的平行线分别与过点B作x轴的平行线和过点B′作x轴的平行线相交于点M,N,
∵∠BAB′=90°,
∴∠BAM+∠B′AN=90°,
又∵∠BAM+∠ABM=90°,
∴∠ABM=∠B′AN.
在△ABM和△B′AN中,
,
∴△ABM≌△B′AN(AAS),
∴B′N=AM=1,AN=BM=3,
∴点B′的坐标为(4,1).
故答案为:(4,1).
【点评】本题考查坐标与图形变化﹣旋转,熟知图形旋转的性质是解题的关键.
10.(2024秋 南海区期中)如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A的坐标是(a,b),经过第1次变换后所得的点A1的坐标是(a,﹣b),则经过第2024次变换后所得的点A2024的坐标是 (a,b) .
【考点】坐标与图形变化﹣对称;规律型:点的坐标;关于x轴、y轴对称的点的坐标.
【专题】规律型;平移、旋转与对称;推理能力.
【答案】(a,b).
【分析】图观察图形可知每四次对称为一个循环组依次循环,用2024除以4,然后根据商的情况确定出变换后的点A所在的象限,然后解答即可.
【解答】解:点A第一次关于x轴对称后在第四象限,
点A第二次关于y轴对称后在第三象限,
点A第三次关于x轴对称后在第二象限,
点A第四次关于y轴对称后在第一象限,
即点A回到原始位置,
所以,每四次对称为一个循环组依次循环,
∵2024÷4=506,
∴经过第2024次变换后所得的A点与第四次变换的位置相同,在第一象限,即回到原始位置,
坐标为(a,b).
故答案为:(a,b).
【点评】本题考查了轴对称的性质,点的坐标变换规律,读懂题目信息,观察出每四次对称为一个循环组依次循环是解题的关键,也是本题的难点.
三.解答题(共5小题)
11.(2024秋 天河区校级期中)①已知a,b,c是一个三角形的三边长,化简|a﹣b+c|+|a﹣b﹣c|.
②已知坐标平面内有两点A(2a﹣b,a+3),B(2b﹣1,﹣a+b),若点A、B关于x轴对称,求(﹣a+2b)2024的值.
【考点】关于x轴、y轴对称的点的坐标;绝对值;三角形三边关系.
【专题】平面直角坐标系;运算能力.
【答案】①2c;②1.
【分析】①根据三角形三边关系得到a﹣b﹣c<0,a﹣b+c>0,再去绝对值,合并同类项即可求解.
②根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”列方程组求出a、b的值,然后代入代数式进行计算即可得解.
【解答】解:①a﹣b﹣c=a﹣(b+c)<0,a﹣b+c=a+c﹣b>0,
|a﹣b+c|+|a﹣b﹣c|=a﹣b+c﹣a+b+c=2c.
②∵点A、B关于x轴对称,
∴,
∴,
∴(﹣a+2b)2024=(5﹣6)2024=1.
【点评】本题考查了解二元一次方程组,轴对称的性质,三角形三边关系,绝对值的性质,关于x、y轴对称的点的坐标特征:点P(x,y)关于x轴的对称点P′的坐标是(x,﹣y).点P(x,y)关于y轴的对称点P′的坐标是(﹣x,y),正确掌握相关性质内容是解题的关键.
12.(2024秋 金水区校级期中)如图,方格纸中每个小方格都是边长为1个单位长度的正方形,平面直角坐标系上,点B的坐标为(1,1).
(1)请直接写出点A、C两点的坐标A (﹣4,1) ,C (﹣3,3) ;
(2)依次连接A,B,C,A,得到△ABC,请直接写出△ABC的形状是 直角 三角形;
(3)若点C与点D关于直线AB对称,则点D的坐标为 (﹣3,﹣1) ;
(4)点F在y轴上,若△ABF与△ABD的面积相等,则点F的坐标为 (0,3)或(0,﹣1) .
【考点】坐标与图形变化﹣对称;勾股定理;勾股定理的逆定理.
【专题】平面直角坐标系;平移、旋转与对称;几何直观.
【答案】(1)(﹣4,1),(﹣3,3);
(2)直角;
(3)(﹣3,﹣1);
(4)(0,3)或(0,﹣1).
【分析】(1)根据所给平面直角坐标系,写出点A和点C的坐标即可解决问题.
(2)根据所给网格,利用勾股定理及其逆定理即可解决问题.
(3)根据轴对称的性质即可解决问题.
(4)根据△ABF与△ABD的面积相等,得出点F到AB的距离与点D到AB的距离相等,据此可解决问题.
【解答】解:(1)由所给平面直角坐标系可知,
点A坐标为(﹣4,1),点C坐标为(﹣3,3).
故答案为:(﹣4,1),(﹣3,3).
(2)如图所示,
由勾股定理得,
AC2=12+22=5,BC2=22+42=20,5≠20,
又因为AB2=52=25,
所以AC2+BC2=AB2,
所以△ABC是直角三角形,
故答案为:直角.
(3)因为3﹣1=2,1﹣2=﹣1,
所以点C关于直线AB的对称点D的坐标为(﹣3,﹣1).
故答案为:(﹣3,﹣1).
(4)因为△ABF与△ABD的面积相等,
所以点F到AB的距离与点D到AB的距离相等.
又因为1﹣(﹣1)=2,
则点F到AB的距离为2,
所以1+2=3,1﹣2=﹣1,
所以点F的坐标为(0,3)或(0,﹣1).
故答案为:(0,3)或(0,﹣1).
【点评】本题主要考查了坐标与图形变化﹣对称、勾股定理及勾股定理的逆定理,熟知轴对称的性质及勾股定理与其逆定理是解题的关键.
13.(2024秋 蓝田县期中)在平面直角坐标系中,已知点A(2m+7,m).
(1)若点A在x轴上,求m的值;
(2)若点A在第四象限且到两坐标轴的距离之和为4,求m的值.
【考点】点的坐标.
【专题】平面直角坐标系;运算能力.
【答案】(1)m=0;
(2)m=﹣3.
【分析】(1)根据x轴上的点的纵坐标为0可得答案;
(2)根据A到两坐标轴的距离之和为4列出绝对值方程,再根据A在第四象限去绝对值解方程即可.
【解答】解:(1)∵点A在x轴上,
∴m=0;
(2)∵点A(2m+7,m)在第四象限且到两坐标轴的距离之和为4,
∴A的横坐标为正,纵坐标为负,|2m+7|+|m|=4,
∴2m+7﹣m=4,
∴m=﹣3.
【点评】本题考查点的坐标,关键是掌握坐标轴上的点的坐标特征,点到坐标轴的距离.
14.(2024秋 新民市期末)如图所示,在平面直角坐标系中,已知A(0,1),B(2,0),C(4,3).
(1)在平面直角坐标系中画出△ABC,则△ABC的面积是 4 ;
(2)若点D与点C关于原点对称,则点D的坐标为 (﹣4,﹣3) ;
(3)已知P为x轴上一点,若△ABP的面积为4,求点P的坐标.
【考点】关于原点对称的点的坐标;三角形的面积.
【专题】平面直角坐标系;运算能力.
【答案】(1)4;
(2)(﹣4,﹣3);
(3)(10,0)或(﹣6,0).
【分析】(1)直接利用△ABC所在矩形面积减去周围三角形面积进而得出答案;
(2)利用关于原点对称点的性质得出答案;
(3)利用三角形面积求法得出符合题意的答案.
【解答】解:(1)如图所示:△ABC的面积是:3×4;
故答案为:4;
(2)点D与点C关于原点对称,则点D的坐标为:(﹣4,﹣3);
故答案为:(﹣4,﹣3);
(3)∵P为x轴上一点,△ABP的面积为4,
∴BP=8,
∴点P的横坐标为:2+8=10或2﹣8=﹣6,
故P点坐标为:(10,0)或(﹣6,0).
【点评】此题主要考查了三角形面积求法以及关于y轴对称点的性质,正确得出对应点位置是解题关键.
15.(2024秋 鹰潭期末)如图,在平面直角坐标系xOy中,点A的坐标为(﹣4,4),点B的坐标为(﹣2,0),点C的坐标为(﹣1,2).
(1)请画出△ABC关于y轴的对称图形△A1B1C1;
(2)直接写出A1,B1,C1三点的坐标;
(3)求△ABC的面积.
【考点】关于x轴、y轴对称的点的坐标;三角形的面积.
【专题】作图题;平面直角坐标系;几何直观.
【答案】见试题解答内容
【分析】(1)关于y轴对称的点,横坐标互为相反数,纵坐标不变;根据轴对称的性质作图即可;
(2)由(1)可得答案;
(3)利用割补法求三角形的面积即可.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)由(1)得A1(4,4),B1(2,0),C1(1,2);
(3)△ABC的面积为3×44.
【点评】本题考查作图﹣轴对称变换、三角形的面积,熟练掌握轴对称的性质是解答本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
