24.4解直角三角形(预习衔接.夯实基础.含解析)-2025-2026学年九年级上册数学华东师大版
文档属性
| 名称 | 24.4解直角三角形(预习衔接.夯实基础.含解析)-2025-2026学年九年级上册数学华东师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 392.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 21:22:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
预习衔接.夯实基础 解直角三角形
一.选择题(共5小题)
1.(2024秋 莱芜区期中)如图,把一个长方形卡片ABCD放在每格宽度为1的横格纸中,恰好四个顶点都在横格线上,已知α=37°,则BC的长为(参考数据:)( )
A. B.4 C.5 D.
2.(2024秋 黄浦区期中)如图,在△ABC中,CD是边AB上的高,已知∠ACB=90°,BC=1.下列线段中,其长为sinA的是( )
A.BD B.AC C.BC D.AD
3.(2024秋 惠阳区期中)正定凌霄塔是全国重点文物保护单位.其造型优美端庄,八角九层,塔高约40米,如图①、如图②所示的正八边形是凌霄塔其中一层的平面示意图,其每个内角的度数为( )
A.80° B.100° C.120° D.135°
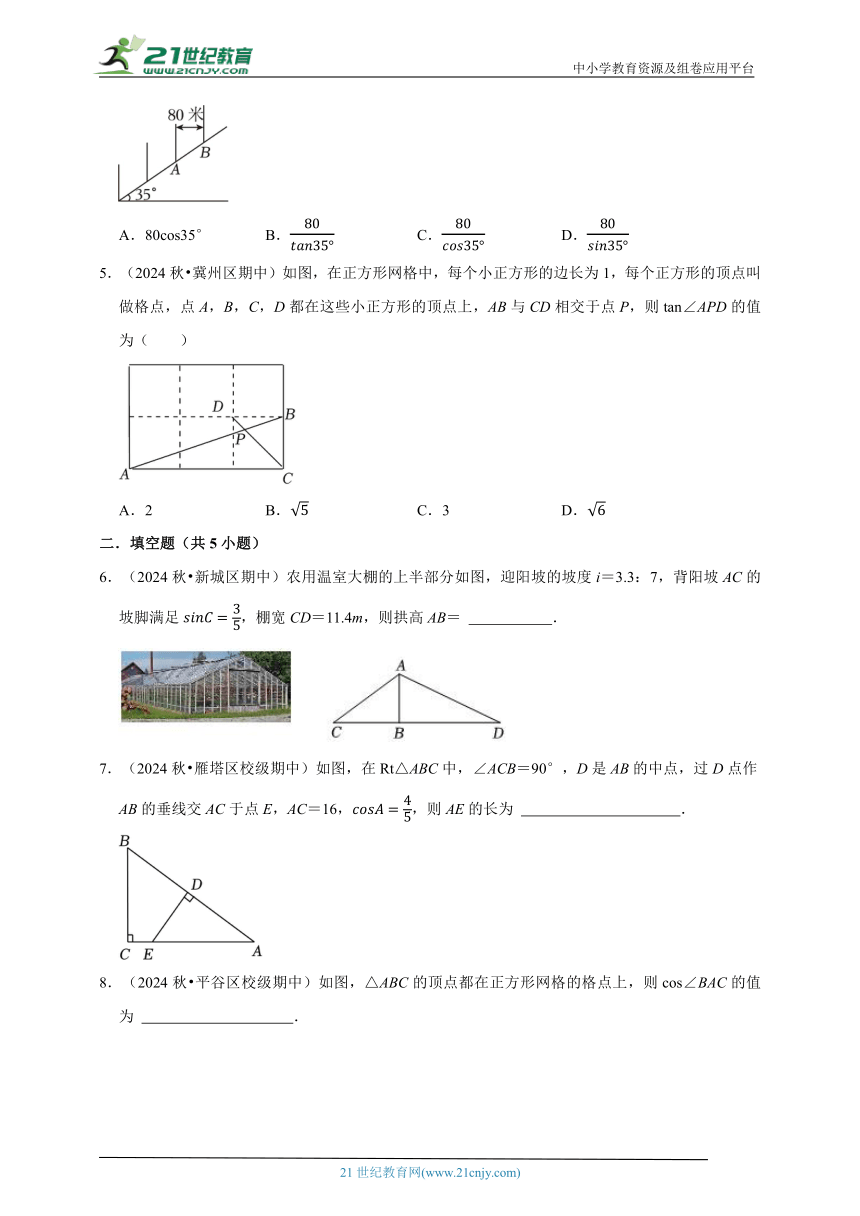
4.(2024 绥江县二模)如图,某登山队在攀登一座坡角为35°的山,每爬上一段山坡就会插一根标杆作为标记,每相邻两根标杆之间的水平距离为80米,那么这两根标杆在坡面上的距离AB为( )
A.80cos35° B. C. D.
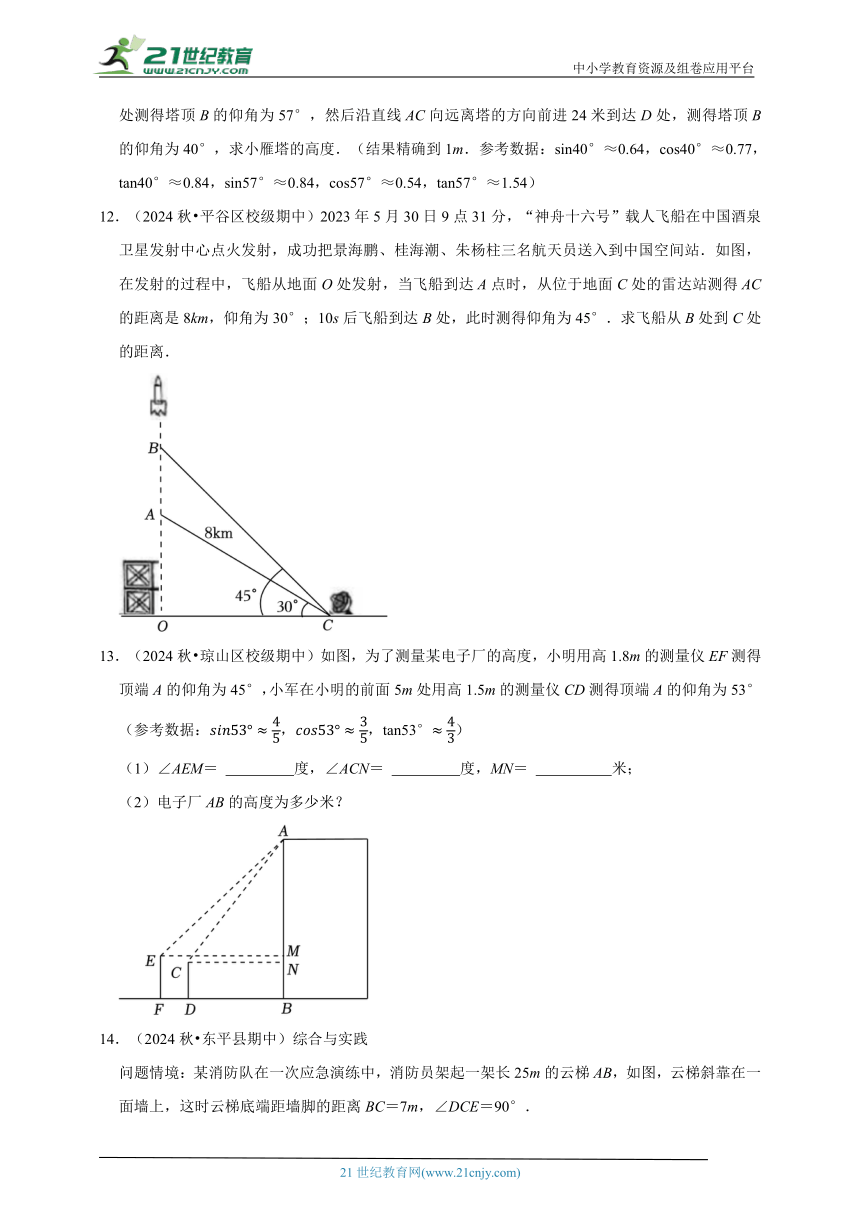
5.(2024秋 冀州区期中)如图,在正方形网格中,每个小正方形的边长为1,每个正方形的顶点叫做格点,点A,B,C,D都在这些小正方形的顶点上,AB与CD相交于点P,则tan∠APD的值为( )
A.2 B. C.3 D.
二.填空题(共5小题)
6.(2024秋 新城区期中)农用温室大棚的上半部分如图,迎阳坡的坡度i=3.3:7,背阳坡AC的坡脚满足,棚宽CD=11.4m,则拱高AB= .
7.(2024秋 雁塔区校级期中)如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,AC=16,,则AE的长为 .
8.(2024秋 平谷区校级期中)如图,△ABC的顶点都在正方形网格的格点上,则cos∠BAC的值为 .
9.(2024 梧州模拟)如图,要测量一座小山丘的高度,某同学在一平面内取A、B两点,且测得与山顶C点的仰角的角度为α、β,A、B两点的距离是a,过C点作CD⊥AB交AB的延长线于点D.则CD的高度h= .(用含有α、β、a的式子表示)
10.(2024秋 淮安区期中)为了测量一幢高楼的高度,在旗杆CD与楼之间选定一点P.测得旗杆顶C的视线PC与地面的夹角∠DPC=21°,测楼顶A的视线PA与地面的夹角∠APB=69°,量得点P到楼底的距离PB与旗杆CD的高度都等于12米,量得旗杆与楼之间距离为DB=30米,则高楼的高度大约为 米.
三.解答题(共5小题)
11.(2024秋 碑林区校级期中)小雁塔是中国早期方形密檐式砖塔的典型作品,塔形秀丽,被国务院公布为第一批全国重点文物保护单位.
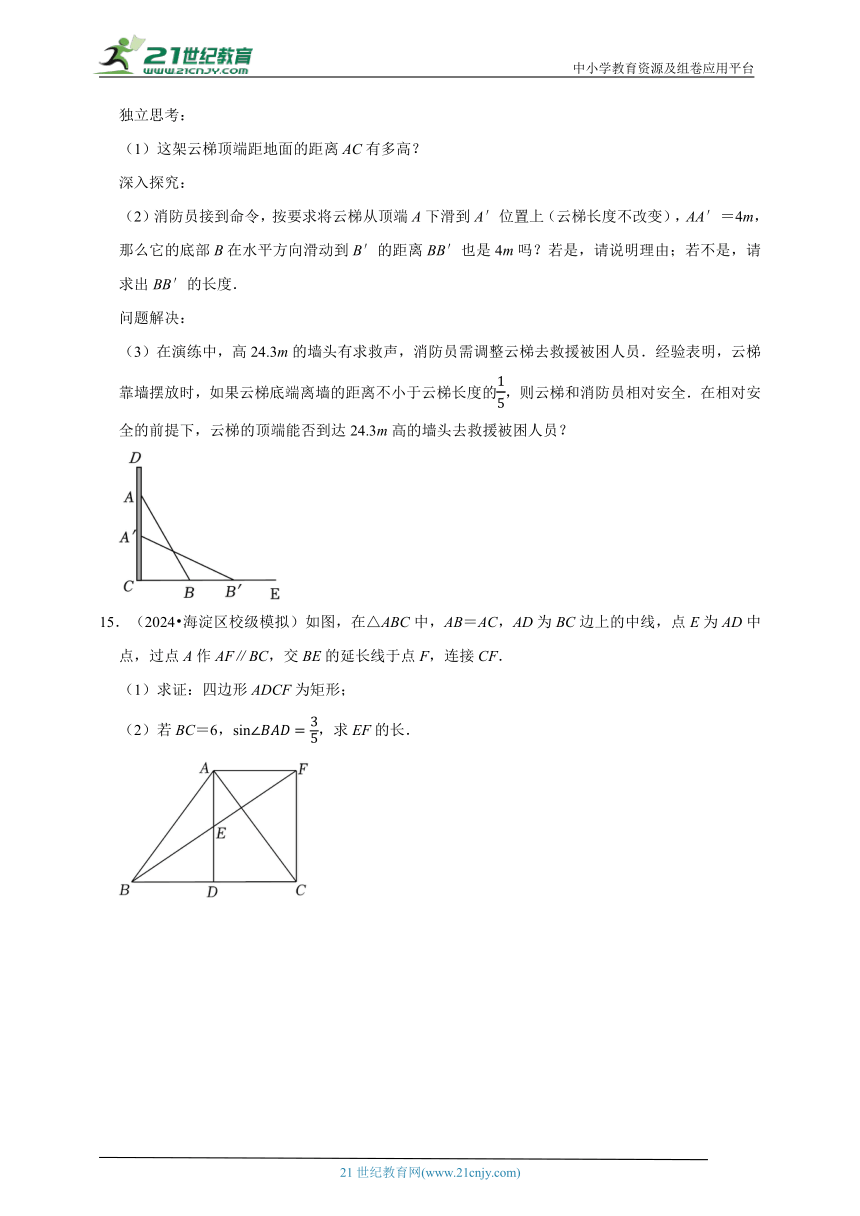
国庆假期,小红利用所学知识来测量塔的高度,测角仪和塔底A在同一水平面,如图,她先在C处测得塔顶B的仰角为57°,然后沿直线AC向远离塔的方向前进24米到达D处,测得塔顶B的仰角为40°,求小雁塔的高度.(结果精确到1m.参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin57°≈0.84,cos57°≈0.54,tan57°≈1.54)
12.(2024秋 平谷区校级期中)2023年5月30日9点31分,“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射,成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站.如图,在发射的过程中,飞船从地面O处发射,当飞船到达A点时,从位于地面C处的雷达站测得AC的距离是8km,仰角为30°;10s后飞船到达B处,此时测得仰角为45°.求飞船从B处到C处的距离.
13.(2024秋 琼山区校级期中)如图,为了测量某电子厂的高度,小明用高1.8m的测量仪EF测得顶端A的仰角为45°,小军在小明的前面5m处用高1.5m的测量仪CD测得顶端A的仰角为53°(参考数据:,,tan53°)
(1)∠AEM= 度,∠ACN= 度,MN= 米;
(2)电子厂AB的高度为多少米?
14.(2024秋 东平县期中)综合与实践
问题情境:某消防队在一次应急演练中,消防员架起一架长25m的云梯AB,如图,云梯斜靠在一面墙上,这时云梯底端距墙脚的距离BC=7m,∠DCE=90°.
独立思考:
(1)这架云梯顶端距地面的距离AC有多高?
深入探究:
(2)消防员接到命令,按要求将云梯从顶端A下滑到A′位置上(云梯长度不改变),AA′=4m,那么它的底部B在水平方向滑动到B′的距离BB′也是4m吗?若是,请说明理由;若不是,请求出BB′的长度.
问题解决:
(3)在演练中,高24.3m的墙头有求救声,消防员需调整云梯去救援被困人员.经验表明,云梯靠墙摆放时,如果云梯底端离墙的距离不小于云梯长度的,则云梯和消防员相对安全.在相对安全的前提下,云梯的顶端能否到达24.3m高的墙头去救援被困人员?
15.(2024 海淀区校级模拟)如图,在△ABC中,AB=AC,AD为BC边上的中线,点E为AD中点,过点A作AF∥BC,交BE的延长线于点F,连接CF.
(1)求证:四边形ADCF为矩形;
(2)若BC=6,sin,求EF的长.
预习衔接.夯实基础 解直角三角形
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 莱芜区期中)如图,把一个长方形卡片ABCD放在每格宽度为1的横格纸中,恰好四个顶点都在横格线上,已知α=37°,则BC的长为(参考数据:)( )
A. B.4 C.5 D.
【考点】解直角三角形的应用;锐角三角函数的定义.
【专题】图形的相似;推理能力.
【答案】C
【分析】过B点作横格线得垂线,交过A点、C点的横格线分别于E、F点,如图,BE=2,BF=4,再证明∠CBF=∠BAE=37°,接着在Rt△BFC中利用正切的定义求出CF的长,然后利用勾股定理计算出BC的长.
【解答】解:过B点作横格线得垂线,交过A点、C点的横格线分别于E、F点,如图,
则BE=2,BF=4,∠AEB=∠BFC=90°,
∵∠ABE+∠BAE=90°,∠ABE+∠CBF=90°,
∴∠CBF=∠BAE=37°,
在Rt△BFC中,tan∠CBFtan37°,
∴CF4=3,
∴BC5.
故选:C.
【点评】本题考查了解直角三角形的应用,构建Rt△ABE和Rt△BCF是解决问题的关键.
2.(2024秋 黄浦区期中)如图,在△ABC中,CD是边AB上的高,已知∠ACB=90°,BC=1.下列线段中,其长为sinA的是( )
A.BD B.AC C.BC D.AD
【考点】解直角三角形.
【专题】解直角三角形及其应用;运算能力.
【答案】A
【分析】根据“同角的余角相等”得出∠BCD=∠A,再根据正弦的定义即可解决问题.
【解答】解:∵CD是边AB上的高,
∴CD⊥AB,
∴∠A+∠ACD=90°.
又∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∴∠A=∠BCD.
在Rt△BCD中,
sin∠BCD.
∵BC=1,
∴sin∠BCD=BD,
即sinA=BD.
故选:A.
【点评】本题主要考查了解直角三角形,熟知正弦的定义及“同角的余角相等”是解题的关键.
3.(2024秋 惠阳区期中)正定凌霄塔是全国重点文物保护单位.其造型优美端庄,八角九层,塔高约40米,如图①、如图②所示的正八边形是凌霄塔其中一层的平面示意图,其每个内角的度数为( )
A.80° B.100° C.120° D.135°
【考点】解直角三角形的应用;多边形内角与外角.
【专题】正多边形与圆;运算能力;推理能力.
【答案】D
【分析】设图中的正多边形为正八边形ABCDEFGH,作出它的一个外角∠ABL,则8∠ABL=360°,求得∠ABL=45°,则∠ABC=135°,于是得到问题的答案.
【解答】解:如图②,延长CB到点L,
∵正多边形的每个外角都相等,八边形ABCDEFGH是正八边形,
∴8∠ABL=360°,
∴∠ABL=45°,
∴∠ABC=180°﹣∠ABL=180°﹣45°=135°,
∴正八边形ABCDEFGH的每个内角的度数都是135°,
故选:D.
【点评】此题重点考查多边形内角与外角、正多边形的性质等知识,正确地求出正八边形的一个外角的度数是解题的关键.
4.(2024 绥江县二模)如图,某登山队在攀登一座坡角为35°的山,每爬上一段山坡就会插一根标杆作为标记,每相邻两根标杆之间的水平距离为80米,那么这两根标杆在坡面上的距离AB为( )
A.80cos35° B. C. D.
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;应用意识.
【答案】C
【分析】根据余弦的定义计算,得到答案.
【解答】解:由题意可知:在Rt△ABC中,∠BAC=35°,AC=80米,
∵cos∠BAC,
∴AB(米),
故选:C.
【点评】本题考查的是解直角三角形的应用﹣坡度坡角问题,熟记锐角三角函数定义是解题的关键.
5.(2024秋 冀州区期中)如图,在正方形网格中,每个小正方形的边长为1,每个正方形的顶点叫做格点,点A,B,C,D都在这些小正方形的顶点上,AB与CD相交于点P,则tan∠APD的值为( )
A.2 B. C.3 D.
【考点】解直角三角形;正方形的性质;相似三角形的判定与性质.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;图形的相似;几何直观;推理能力.
【答案】A
【分析】连接BE交CD于点F,由正方形的性质得DF=CFCD,BFBE,CD=BE,BE⊥CD,进而得BF=CF=DF,证得△ACP∽△BDP,得DP:CP=BD:AC=1:3,从而得到DP=PFCFBF,进而利用正切定义解答即可.
【解答】解:如图,连接BE交CD于点F,
∵四边形BCED是正方形,
∴DF=CFCD,BFBE,CD=BE,BE⊥CD,
∴BF=CF=DF,
根据题意,AC∥BD,
∴∠ACP=∠BDP,∠DBP=∠CAP,
∴△ACP∽△BDP,
∴DP:CP=BD:AC=1:3,
∵BF=CF=DF,
∴DP:DF=1:2,
∴DP=PFCFBF,
在Rt△PBF中,tan∠BPF2,
∵∠APD=∠BPF,
∴tan∠APD=2.
故选:A.
【点评】本题主要考查了解直角三角形,正方形的性质,相似三角形的判定与性质,熟练掌握相似三角形的判定及性质是解题的关键.
二.填空题(共5小题)
6.(2024秋 新城区期中)农用温室大棚的上半部分如图,迎阳坡的坡度i=3.3:7,背阳坡AC的坡脚满足,棚宽CD=11.4m,则拱高AB= 3.3m .
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】3.3m.
【分析】设AB=h,根据正弦和勾股定理可得,再根据坡度可得,最后根据CD=CB+BD=11.4列方程求解即可.
【解答】解:设AB=h,
∵,
∴,
解得:,
∴,
∵迎阳坡的坡度i=3.3:7,
∴,即
,解得:,
∵CD=CB+BD=11.4,
∴,
解得:h=3.3.
故答案为:3.3m.
【点评】本题主要考查了解直角三角形的应用、正弦、坡度等知识点,灵活运用正弦和坡度的知识是解题的关键.
7.(2024秋 雁塔区校级期中)如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,AC=16,,则AE的长为 .
【考点】解直角三角形;线段垂直平分线的性质.
【专题】三角形;运算能力.
【答案】.
【分析】根据三角函数求出AB,从而由线段中点的定义求出AD,再由三角函数求出AE即可.
【解答】解:∵AC=16,
∴cosA,
∴AB=20,
∵D是AB的中点,
∴ADAB=10,
∴cosA,
∴AE.
故答案为:.
【点评】本题考查解直角三角形、线段垂直平分线的性质,掌握三角函数、线段中点的定义是解题的关键.
8.(2024秋 平谷区校级期中)如图,△ABC的顶点都在正方形网格的格点上,则cos∠BAC的值为 .
【考点】解直角三角形.
【专题】解直角三角形及其应用;应用意识.
【答案】.
【分析】根据锐角三角函数的定义即可求出答案.
【解答】解:过B作BH⊥AC交AC的延长线于H,
∴AB5,AH=3,
∴cos∠BAC,
故答案为:.
【点评】本题考查锐角三角函数,解题的关键是熟练运用锐角三角函数的定义,本题属于基础题型.
9.(2024 梧州模拟)如图,要测量一座小山丘的高度,某同学在一平面内取A、B两点,且测得与山顶C点的仰角的角度为α、β,A、B两点的距离是a,过C点作CD⊥AB交AB的延长线于点D.则CD的高度h= .(用含有α、β、a的式子表示)
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】.
【分析】根据垂直定义可得:∠CDA=90°,然后分别在Rt△ACD和Rt△CBD中,利用锐角三角函数的定义求出AD和BD的长,从而列出关于h的方程,进行计算即可解答.
【解答】解:∵CD⊥AB,
∴∠CDA=90°,
在Rt△ACD中,∠CAD=α,CD=h,
∴AD,
在Rt△CBD中,∠CBD=β,
∴BD,
∵AD﹣BD=AB,
∴a,
∴tanβh﹣tanαh=atanαtanβ,
∴h,
∴CD的高度h为,
故答案为:.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
10.(2024秋 淮安区期中)为了测量一幢高楼的高度,在旗杆CD与楼之间选定一点P.测得旗杆顶C的视线PC与地面的夹角∠DPC=21°,测楼顶A的视线PA与地面的夹角∠APB=69°,量得点P到楼底的距离PB与旗杆CD的高度都等于12米,量得旗杆与楼之间距离为DB=30米,则高楼的高度大约为 18 米.
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】18.
【分析】根据题意可得:CD⊥DB,AB⊥DB,从而可得∠CDP=∠ABP=90°,再利用直角三角形的两个锐角互余可得∠PAB=21°,从而可得∠PAB=∠CPD=21°,然后根据AAS证明△BAP≌△DPC,从而利用全等三角形的性质可得DP=AB=18米,即可解答.
【解答】解:由题意得:CD⊥DB,AB⊥DB,
∴∠CDP=∠ABP=90°,
∵∠APB=69°,
∴∠PAB=90°﹣∠APB=21°,
∵∠CPD=21°,
∴∠PAB=∠CPD=21°,
∵DB=30米,PB=12米,
∴DP=BD﹣BP=18(米),
在△BAP和△DPC中,
,
∴△BAP≌△DPC(AAS),
∴DP=AB=18米,
故答案为:18.
【点评】本题考查了解直角三角形,熟练掌握全等三角形的判定与性质是解题的关键.
三.解答题(共5小题)
11.(2024秋 碑林区校级期中)小雁塔是中国早期方形密檐式砖塔的典型作品,塔形秀丽,被国务院公布为第一批全国重点文物保护单位.
国庆假期,小红利用所学知识来测量塔的高度,测角仪和塔底A在同一水平面,如图,她先在C处测得塔顶B的仰角为57°,然后沿直线AC向远离塔的方向前进24米到达D处,测得塔顶B的仰角为40°,求小雁塔的高度.(结果精确到1m.参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin57°≈0.84,cos57°≈0.54,tan57°≈1.54)
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】小雁塔的高度约为44米.
【分析】根据题意可得:BA⊥AD,CD=24米,然后设AC=x米,则AD=(x+24)米,再分别在Rt△ABC和Rt△ABD中,利用锐角三角函数的定义求出AB的长,从而列出关于x的方程进行计算,即可解答.
【解答】解:由题意得:BA⊥AD,CD=24米,
设AC=x米,则AD=AC+CD=(x+24)米,
在Rt△ABC中,∠ACB=57°,
∴AB=AC tan57°≈1.54x(米),
在Rt△ABD中,∠ADB=40°,
∴AB=AD tan40°≈0.84(x+24),
∴1.54x=0.84(x+24),
解得:x=28.8,
∴AB=1.54x≈44(米),
∴小雁塔的高度约为44米.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
12.(2024秋 平谷区校级期中)2023年5月30日9点31分,“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射,成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站.如图,在发射的过程中,飞船从地面O处发射,当飞船到达A点时,从位于地面C处的雷达站测得AC的距离是8km,仰角为30°;10s后飞船到达B处,此时测得仰角为45°.求飞船从B处到C处的距离.
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;运算能力;应用意识.
【答案】4km.
【分析】根据题意可得:BO⊥OC,然后在Rt△AOC中,利用含30度角的直角三角形的性质可求出AO和OC的长,再在Rt△BOC中,解直角三角形即可求出BC.
【解答】解:由题意得:BO⊥OC,
在Rt△AOC中,AC=8km,∠ACO=30°,
∴AOAC=4km,
∴OC4km,
在Rt△BOC中,∠BCO=45°,
∴∠B=45°=∠BCO,
∴OB=OC=4km,
∴BC4km.
答:飞船从B处到C处的距离为4km.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
13.(2024秋 琼山区校级期中)如图,为了测量某电子厂的高度,小明用高1.8m的测量仪EF测得顶端A的仰角为45°,小军在小明的前面5m处用高1.5m的测量仪CD测得顶端A的仰角为53°(参考数据:,,tan53°)
(1)∠AEM= 45 度,∠ACN= 53 度,MN= 0.3 米;
(2)电子厂AB的高度为多少米?
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】(1)45;53;0.3;
(2)电子厂AB的高度为22.7m.
【分析】(1)根据题意可得:∠AEM=45°,∠ACN=53°,EF=BM=1.8m,CD=BN=1.5m,然后利用线段的和差关系进行计算,即可解答;
(2)根据题意可得:EM=BF,CN=BD,DF=5m,从而可设EM=BF=x m,则BD=CN=(x﹣5)m,然后分别在Rt△AEM和Rt△ACN中,利用锐角三角函数的定义求出AM和AN的长,从而列出关于x的方程进行计算,即可解答.
【解答】解:(1)由题意得:∠AEM=45°,∠ACN=53°,EF=BM=1.8m,CD=BN=1.5m,
∴MN=BM﹣BN=1.8﹣1.5=0.3(m),
故答案为:45;53;0.3;
(2)由题意得:EM=BF,CN=BD,DF=5m,
设EM=BF=x m,则BD=CN=(x﹣5)m,
在Rt△AEM中,∠AEM=45°,
∴AM=EM tan45°=x(m),
在Rt△ACN中,∠ACN=53°,
∴AN=CN tan53°(x﹣5)m,
∵AM+MB=AN+BN,
∴x+1.8(x﹣5)+1.5,
解得:x=20.9,
∴AM=20.9m,
∴AB=AM+BM=20.9+1.8=22.7(m),
∴电子厂AB的高度为22.7m.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
14.(2024秋 东平县期中)综合与实践
问题情境:某消防队在一次应急演练中,消防员架起一架长25m的云梯AB,如图,云梯斜靠在一面墙上,这时云梯底端距墙脚的距离BC=7m,∠DCE=90°.
独立思考:
(1)这架云梯顶端距地面的距离AC有多高?
深入探究:
(2)消防员接到命令,按要求将云梯从顶端A下滑到A′位置上(云梯长度不改变),AA′=4m,那么它的底部B在水平方向滑动到B′的距离BB′也是4m吗?若是,请说明理由;若不是,请求出BB′的长度.
问题解决:
(3)在演练中,高24.3m的墙头有求救声,消防员需调整云梯去救援被困人员.经验表明,云梯靠墙摆放时,如果云梯底端离墙的距离不小于云梯长度的,则云梯和消防员相对安全.在相对安全的前提下,云梯的顶端能否到达24.3m高的墙头去救援被困人员?
【考点】解直角三角形的应用;勾股定理的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】见试题解答内容
【分析】(1)由图可以看出梯子墙地可围成一个直角三角形,即梯子为斜边,将梯子底部到墙的距离线段对应为一个直角边,梯子顶端到地的距离线段对应为另一个直角边,所以梯子顶端到地的距离为252﹣72=242,所以梯子顶端到地为24米;
(2)求出BB'的长度即可;
(3)先求出梯子能够到达墙面的最大高度,再与24.3比较即可.
【解答】解:(1)在Rt△ACB中,
∴AC24m,
答:这架云梯顶端距地面的距离AC有24m.
(2)云梯的底部B在水平方向滑动到B′的距离BB′不是4m.理由如下:
由(1)可知AC=24m,
∴A′C=AC﹣AA′=24﹣4=20m.
在Rt△A′CB′中,
∴,
∴BB′=CB′﹣BC=15﹣7=8m.
(3)若云梯底端离墙的距离刚好为云梯长度的,
则能够到达墙面的最大高度为.
∵24.32=590.49<600,
∴,
∴在相对安全的前提下,云梯的顶端能到达24.3m高的墙头去救援被困人员.
【点评】本题考查勾股定理和解直角三角形,熟练掌握勾股定理是解题关键.
15.(2024 海淀区校级模拟)如图,在△ABC中,AB=AC,AD为BC边上的中线,点E为AD中点,过点A作AF∥BC,交BE的延长线于点F,连接CF.
(1)求证:四边形ADCF为矩形;
(2)若BC=6,sin,求EF的长.
【考点】解直角三角形;等腰三角形的性质;矩形的判定与性质.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;解直角三角形及其应用;运算能力;推理能力.
【答案】见试题解答内容
【分析】(1)先证△AFE≌△DBE(AAS),得出AF=BD,则AF=DC,得出四边形ADCF为平行四边形,再证∠ADC=90°,即可得出结论;
(2)BC=6,AD为BC边上的中线,则,在Rt△ABD 中,,求出,则,又根据点E为AD中点,求出,则EF可根据勾股定理可求.
【解答】(1)证明:∵AD是BC边上的中线,
∴BD=CD,
∵点E是AD的中点,
∴AE=ED,
∵AF∥BC,
∴∠AFE=∠DBE,∠FAE=∠BDE,
在△AFE和△DBE中,
,
∴△AFE≌△DBE(AAS),
∴AF=BD,
∴AF=DC,
又∵AF∥BC,
∴四边形ADCF为平行四边形,
∵AB=AC,AD为BC边上的中线,
∴AD⊥BC,
∴∠ADC=90°,
∴四边形ADCF为矩形;
(2)解:∵BC=6,AD为BC边上的中线,
∴,
∵在Rt△ABD 中,,
∴,
∴,
又∵点E为AD中点,
∴,
∴在 Rt△EBD中,,
∴.
【点评】本题考查了平行四边形的判定、矩形的判定与性质、全等三角形的判定与性质、勾股定理、等腰三角形的性质、锐角三角函数定义等知识;熟练掌握全等三角形的判定与性质和勾股定理是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.夯实基础 解直角三角形
一.选择题(共5小题)
1.(2024秋 莱芜区期中)如图,把一个长方形卡片ABCD放在每格宽度为1的横格纸中,恰好四个顶点都在横格线上,已知α=37°,则BC的长为(参考数据:)( )
A. B.4 C.5 D.
2.(2024秋 黄浦区期中)如图,在△ABC中,CD是边AB上的高,已知∠ACB=90°,BC=1.下列线段中,其长为sinA的是( )
A.BD B.AC C.BC D.AD
3.(2024秋 惠阳区期中)正定凌霄塔是全国重点文物保护单位.其造型优美端庄,八角九层,塔高约40米,如图①、如图②所示的正八边形是凌霄塔其中一层的平面示意图,其每个内角的度数为( )
A.80° B.100° C.120° D.135°
4.(2024 绥江县二模)如图,某登山队在攀登一座坡角为35°的山,每爬上一段山坡就会插一根标杆作为标记,每相邻两根标杆之间的水平距离为80米,那么这两根标杆在坡面上的距离AB为( )
A.80cos35° B. C. D.
5.(2024秋 冀州区期中)如图,在正方形网格中,每个小正方形的边长为1,每个正方形的顶点叫做格点,点A,B,C,D都在这些小正方形的顶点上,AB与CD相交于点P,则tan∠APD的值为( )
A.2 B. C.3 D.
二.填空题(共5小题)
6.(2024秋 新城区期中)农用温室大棚的上半部分如图,迎阳坡的坡度i=3.3:7,背阳坡AC的坡脚满足,棚宽CD=11.4m,则拱高AB= .
7.(2024秋 雁塔区校级期中)如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,AC=16,,则AE的长为 .
8.(2024秋 平谷区校级期中)如图,△ABC的顶点都在正方形网格的格点上,则cos∠BAC的值为 .
9.(2024 梧州模拟)如图,要测量一座小山丘的高度,某同学在一平面内取A、B两点,且测得与山顶C点的仰角的角度为α、β,A、B两点的距离是a,过C点作CD⊥AB交AB的延长线于点D.则CD的高度h= .(用含有α、β、a的式子表示)
10.(2024秋 淮安区期中)为了测量一幢高楼的高度,在旗杆CD与楼之间选定一点P.测得旗杆顶C的视线PC与地面的夹角∠DPC=21°,测楼顶A的视线PA与地面的夹角∠APB=69°,量得点P到楼底的距离PB与旗杆CD的高度都等于12米,量得旗杆与楼之间距离为DB=30米,则高楼的高度大约为 米.
三.解答题(共5小题)
11.(2024秋 碑林区校级期中)小雁塔是中国早期方形密檐式砖塔的典型作品,塔形秀丽,被国务院公布为第一批全国重点文物保护单位.
国庆假期,小红利用所学知识来测量塔的高度,测角仪和塔底A在同一水平面,如图,她先在C处测得塔顶B的仰角为57°,然后沿直线AC向远离塔的方向前进24米到达D处,测得塔顶B的仰角为40°,求小雁塔的高度.(结果精确到1m.参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin57°≈0.84,cos57°≈0.54,tan57°≈1.54)
12.(2024秋 平谷区校级期中)2023年5月30日9点31分,“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射,成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站.如图,在发射的过程中,飞船从地面O处发射,当飞船到达A点时,从位于地面C处的雷达站测得AC的距离是8km,仰角为30°;10s后飞船到达B处,此时测得仰角为45°.求飞船从B处到C处的距离.
13.(2024秋 琼山区校级期中)如图,为了测量某电子厂的高度,小明用高1.8m的测量仪EF测得顶端A的仰角为45°,小军在小明的前面5m处用高1.5m的测量仪CD测得顶端A的仰角为53°(参考数据:,,tan53°)
(1)∠AEM= 度,∠ACN= 度,MN= 米;
(2)电子厂AB的高度为多少米?
14.(2024秋 东平县期中)综合与实践
问题情境:某消防队在一次应急演练中,消防员架起一架长25m的云梯AB,如图,云梯斜靠在一面墙上,这时云梯底端距墙脚的距离BC=7m,∠DCE=90°.
独立思考:
(1)这架云梯顶端距地面的距离AC有多高?
深入探究:
(2)消防员接到命令,按要求将云梯从顶端A下滑到A′位置上(云梯长度不改变),AA′=4m,那么它的底部B在水平方向滑动到B′的距离BB′也是4m吗?若是,请说明理由;若不是,请求出BB′的长度.
问题解决:
(3)在演练中,高24.3m的墙头有求救声,消防员需调整云梯去救援被困人员.经验表明,云梯靠墙摆放时,如果云梯底端离墙的距离不小于云梯长度的,则云梯和消防员相对安全.在相对安全的前提下,云梯的顶端能否到达24.3m高的墙头去救援被困人员?
15.(2024 海淀区校级模拟)如图,在△ABC中,AB=AC,AD为BC边上的中线,点E为AD中点,过点A作AF∥BC,交BE的延长线于点F,连接CF.
(1)求证:四边形ADCF为矩形;
(2)若BC=6,sin,求EF的长.
预习衔接.夯实基础 解直角三角形
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 莱芜区期中)如图,把一个长方形卡片ABCD放在每格宽度为1的横格纸中,恰好四个顶点都在横格线上,已知α=37°,则BC的长为(参考数据:)( )
A. B.4 C.5 D.
【考点】解直角三角形的应用;锐角三角函数的定义.
【专题】图形的相似;推理能力.
【答案】C
【分析】过B点作横格线得垂线,交过A点、C点的横格线分别于E、F点,如图,BE=2,BF=4,再证明∠CBF=∠BAE=37°,接着在Rt△BFC中利用正切的定义求出CF的长,然后利用勾股定理计算出BC的长.
【解答】解:过B点作横格线得垂线,交过A点、C点的横格线分别于E、F点,如图,
则BE=2,BF=4,∠AEB=∠BFC=90°,
∵∠ABE+∠BAE=90°,∠ABE+∠CBF=90°,
∴∠CBF=∠BAE=37°,
在Rt△BFC中,tan∠CBFtan37°,
∴CF4=3,
∴BC5.
故选:C.
【点评】本题考查了解直角三角形的应用,构建Rt△ABE和Rt△BCF是解决问题的关键.
2.(2024秋 黄浦区期中)如图,在△ABC中,CD是边AB上的高,已知∠ACB=90°,BC=1.下列线段中,其长为sinA的是( )
A.BD B.AC C.BC D.AD
【考点】解直角三角形.
【专题】解直角三角形及其应用;运算能力.
【答案】A
【分析】根据“同角的余角相等”得出∠BCD=∠A,再根据正弦的定义即可解决问题.
【解答】解:∵CD是边AB上的高,
∴CD⊥AB,
∴∠A+∠ACD=90°.
又∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∴∠A=∠BCD.
在Rt△BCD中,
sin∠BCD.
∵BC=1,
∴sin∠BCD=BD,
即sinA=BD.
故选:A.
【点评】本题主要考查了解直角三角形,熟知正弦的定义及“同角的余角相等”是解题的关键.
3.(2024秋 惠阳区期中)正定凌霄塔是全国重点文物保护单位.其造型优美端庄,八角九层,塔高约40米,如图①、如图②所示的正八边形是凌霄塔其中一层的平面示意图,其每个内角的度数为( )
A.80° B.100° C.120° D.135°
【考点】解直角三角形的应用;多边形内角与外角.
【专题】正多边形与圆;运算能力;推理能力.
【答案】D
【分析】设图中的正多边形为正八边形ABCDEFGH,作出它的一个外角∠ABL,则8∠ABL=360°,求得∠ABL=45°,则∠ABC=135°,于是得到问题的答案.
【解答】解:如图②,延长CB到点L,
∵正多边形的每个外角都相等,八边形ABCDEFGH是正八边形,
∴8∠ABL=360°,
∴∠ABL=45°,
∴∠ABC=180°﹣∠ABL=180°﹣45°=135°,
∴正八边形ABCDEFGH的每个内角的度数都是135°,
故选:D.
【点评】此题重点考查多边形内角与外角、正多边形的性质等知识,正确地求出正八边形的一个外角的度数是解题的关键.
4.(2024 绥江县二模)如图,某登山队在攀登一座坡角为35°的山,每爬上一段山坡就会插一根标杆作为标记,每相邻两根标杆之间的水平距离为80米,那么这两根标杆在坡面上的距离AB为( )
A.80cos35° B. C. D.
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;应用意识.
【答案】C
【分析】根据余弦的定义计算,得到答案.
【解答】解:由题意可知:在Rt△ABC中,∠BAC=35°,AC=80米,
∵cos∠BAC,
∴AB(米),
故选:C.
【点评】本题考查的是解直角三角形的应用﹣坡度坡角问题,熟记锐角三角函数定义是解题的关键.
5.(2024秋 冀州区期中)如图,在正方形网格中,每个小正方形的边长为1,每个正方形的顶点叫做格点,点A,B,C,D都在这些小正方形的顶点上,AB与CD相交于点P,则tan∠APD的值为( )
A.2 B. C.3 D.
【考点】解直角三角形;正方形的性质;相似三角形的判定与性质.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;图形的相似;几何直观;推理能力.
【答案】A
【分析】连接BE交CD于点F,由正方形的性质得DF=CFCD,BFBE,CD=BE,BE⊥CD,进而得BF=CF=DF,证得△ACP∽△BDP,得DP:CP=BD:AC=1:3,从而得到DP=PFCFBF,进而利用正切定义解答即可.
【解答】解:如图,连接BE交CD于点F,
∵四边形BCED是正方形,
∴DF=CFCD,BFBE,CD=BE,BE⊥CD,
∴BF=CF=DF,
根据题意,AC∥BD,
∴∠ACP=∠BDP,∠DBP=∠CAP,
∴△ACP∽△BDP,
∴DP:CP=BD:AC=1:3,
∵BF=CF=DF,
∴DP:DF=1:2,
∴DP=PFCFBF,
在Rt△PBF中,tan∠BPF2,
∵∠APD=∠BPF,
∴tan∠APD=2.
故选:A.
【点评】本题主要考查了解直角三角形,正方形的性质,相似三角形的判定与性质,熟练掌握相似三角形的判定及性质是解题的关键.
二.填空题(共5小题)
6.(2024秋 新城区期中)农用温室大棚的上半部分如图,迎阳坡的坡度i=3.3:7,背阳坡AC的坡脚满足,棚宽CD=11.4m,则拱高AB= 3.3m .
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】3.3m.
【分析】设AB=h,根据正弦和勾股定理可得,再根据坡度可得,最后根据CD=CB+BD=11.4列方程求解即可.
【解答】解:设AB=h,
∵,
∴,
解得:,
∴,
∵迎阳坡的坡度i=3.3:7,
∴,即
,解得:,
∵CD=CB+BD=11.4,
∴,
解得:h=3.3.
故答案为:3.3m.
【点评】本题主要考查了解直角三角形的应用、正弦、坡度等知识点,灵活运用正弦和坡度的知识是解题的关键.
7.(2024秋 雁塔区校级期中)如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,AC=16,,则AE的长为 .
【考点】解直角三角形;线段垂直平分线的性质.
【专题】三角形;运算能力.
【答案】.
【分析】根据三角函数求出AB,从而由线段中点的定义求出AD,再由三角函数求出AE即可.
【解答】解:∵AC=16,
∴cosA,
∴AB=20,
∵D是AB的中点,
∴ADAB=10,
∴cosA,
∴AE.
故答案为:.
【点评】本题考查解直角三角形、线段垂直平分线的性质,掌握三角函数、线段中点的定义是解题的关键.
8.(2024秋 平谷区校级期中)如图,△ABC的顶点都在正方形网格的格点上,则cos∠BAC的值为 .
【考点】解直角三角形.
【专题】解直角三角形及其应用;应用意识.
【答案】.
【分析】根据锐角三角函数的定义即可求出答案.
【解答】解:过B作BH⊥AC交AC的延长线于H,
∴AB5,AH=3,
∴cos∠BAC,
故答案为:.
【点评】本题考查锐角三角函数,解题的关键是熟练运用锐角三角函数的定义,本题属于基础题型.
9.(2024 梧州模拟)如图,要测量一座小山丘的高度,某同学在一平面内取A、B两点,且测得与山顶C点的仰角的角度为α、β,A、B两点的距离是a,过C点作CD⊥AB交AB的延长线于点D.则CD的高度h= .(用含有α、β、a的式子表示)
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】.
【分析】根据垂直定义可得:∠CDA=90°,然后分别在Rt△ACD和Rt△CBD中,利用锐角三角函数的定义求出AD和BD的长,从而列出关于h的方程,进行计算即可解答.
【解答】解:∵CD⊥AB,
∴∠CDA=90°,
在Rt△ACD中,∠CAD=α,CD=h,
∴AD,
在Rt△CBD中,∠CBD=β,
∴BD,
∵AD﹣BD=AB,
∴a,
∴tanβh﹣tanαh=atanαtanβ,
∴h,
∴CD的高度h为,
故答案为:.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
10.(2024秋 淮安区期中)为了测量一幢高楼的高度,在旗杆CD与楼之间选定一点P.测得旗杆顶C的视线PC与地面的夹角∠DPC=21°,测楼顶A的视线PA与地面的夹角∠APB=69°,量得点P到楼底的距离PB与旗杆CD的高度都等于12米,量得旗杆与楼之间距离为DB=30米,则高楼的高度大约为 18 米.
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】18.
【分析】根据题意可得:CD⊥DB,AB⊥DB,从而可得∠CDP=∠ABP=90°,再利用直角三角形的两个锐角互余可得∠PAB=21°,从而可得∠PAB=∠CPD=21°,然后根据AAS证明△BAP≌△DPC,从而利用全等三角形的性质可得DP=AB=18米,即可解答.
【解答】解:由题意得:CD⊥DB,AB⊥DB,
∴∠CDP=∠ABP=90°,
∵∠APB=69°,
∴∠PAB=90°﹣∠APB=21°,
∵∠CPD=21°,
∴∠PAB=∠CPD=21°,
∵DB=30米,PB=12米,
∴DP=BD﹣BP=18(米),
在△BAP和△DPC中,
,
∴△BAP≌△DPC(AAS),
∴DP=AB=18米,
故答案为:18.
【点评】本题考查了解直角三角形,熟练掌握全等三角形的判定与性质是解题的关键.
三.解答题(共5小题)
11.(2024秋 碑林区校级期中)小雁塔是中国早期方形密檐式砖塔的典型作品,塔形秀丽,被国务院公布为第一批全国重点文物保护单位.
国庆假期,小红利用所学知识来测量塔的高度,测角仪和塔底A在同一水平面,如图,她先在C处测得塔顶B的仰角为57°,然后沿直线AC向远离塔的方向前进24米到达D处,测得塔顶B的仰角为40°,求小雁塔的高度.(结果精确到1m.参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin57°≈0.84,cos57°≈0.54,tan57°≈1.54)
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】小雁塔的高度约为44米.
【分析】根据题意可得:BA⊥AD,CD=24米,然后设AC=x米,则AD=(x+24)米,再分别在Rt△ABC和Rt△ABD中,利用锐角三角函数的定义求出AB的长,从而列出关于x的方程进行计算,即可解答.
【解答】解:由题意得:BA⊥AD,CD=24米,
设AC=x米,则AD=AC+CD=(x+24)米,
在Rt△ABC中,∠ACB=57°,
∴AB=AC tan57°≈1.54x(米),
在Rt△ABD中,∠ADB=40°,
∴AB=AD tan40°≈0.84(x+24),
∴1.54x=0.84(x+24),
解得:x=28.8,
∴AB=1.54x≈44(米),
∴小雁塔的高度约为44米.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
12.(2024秋 平谷区校级期中)2023年5月30日9点31分,“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射,成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站.如图,在发射的过程中,飞船从地面O处发射,当飞船到达A点时,从位于地面C处的雷达站测得AC的距离是8km,仰角为30°;10s后飞船到达B处,此时测得仰角为45°.求飞船从B处到C处的距离.
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;运算能力;应用意识.
【答案】4km.
【分析】根据题意可得:BO⊥OC,然后在Rt△AOC中,利用含30度角的直角三角形的性质可求出AO和OC的长,再在Rt△BOC中,解直角三角形即可求出BC.
【解答】解:由题意得:BO⊥OC,
在Rt△AOC中,AC=8km,∠ACO=30°,
∴AOAC=4km,
∴OC4km,
在Rt△BOC中,∠BCO=45°,
∴∠B=45°=∠BCO,
∴OB=OC=4km,
∴BC4km.
答:飞船从B处到C处的距离为4km.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
13.(2024秋 琼山区校级期中)如图,为了测量某电子厂的高度,小明用高1.8m的测量仪EF测得顶端A的仰角为45°,小军在小明的前面5m处用高1.5m的测量仪CD测得顶端A的仰角为53°(参考数据:,,tan53°)
(1)∠AEM= 45 度,∠ACN= 53 度,MN= 0.3 米;
(2)电子厂AB的高度为多少米?
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】(1)45;53;0.3;
(2)电子厂AB的高度为22.7m.
【分析】(1)根据题意可得:∠AEM=45°,∠ACN=53°,EF=BM=1.8m,CD=BN=1.5m,然后利用线段的和差关系进行计算,即可解答;
(2)根据题意可得:EM=BF,CN=BD,DF=5m,从而可设EM=BF=x m,则BD=CN=(x﹣5)m,然后分别在Rt△AEM和Rt△ACN中,利用锐角三角函数的定义求出AM和AN的长,从而列出关于x的方程进行计算,即可解答.
【解答】解:(1)由题意得:∠AEM=45°,∠ACN=53°,EF=BM=1.8m,CD=BN=1.5m,
∴MN=BM﹣BN=1.8﹣1.5=0.3(m),
故答案为:45;53;0.3;
(2)由题意得:EM=BF,CN=BD,DF=5m,
设EM=BF=x m,则BD=CN=(x﹣5)m,
在Rt△AEM中,∠AEM=45°,
∴AM=EM tan45°=x(m),
在Rt△ACN中,∠ACN=53°,
∴AN=CN tan53°(x﹣5)m,
∵AM+MB=AN+BN,
∴x+1.8(x﹣5)+1.5,
解得:x=20.9,
∴AM=20.9m,
∴AB=AM+BM=20.9+1.8=22.7(m),
∴电子厂AB的高度为22.7m.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
14.(2024秋 东平县期中)综合与实践
问题情境:某消防队在一次应急演练中,消防员架起一架长25m的云梯AB,如图,云梯斜靠在一面墙上,这时云梯底端距墙脚的距离BC=7m,∠DCE=90°.
独立思考:
(1)这架云梯顶端距地面的距离AC有多高?
深入探究:
(2)消防员接到命令,按要求将云梯从顶端A下滑到A′位置上(云梯长度不改变),AA′=4m,那么它的底部B在水平方向滑动到B′的距离BB′也是4m吗?若是,请说明理由;若不是,请求出BB′的长度.
问题解决:
(3)在演练中,高24.3m的墙头有求救声,消防员需调整云梯去救援被困人员.经验表明,云梯靠墙摆放时,如果云梯底端离墙的距离不小于云梯长度的,则云梯和消防员相对安全.在相对安全的前提下,云梯的顶端能否到达24.3m高的墙头去救援被困人员?
【考点】解直角三角形的应用;勾股定理的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】见试题解答内容
【分析】(1)由图可以看出梯子墙地可围成一个直角三角形,即梯子为斜边,将梯子底部到墙的距离线段对应为一个直角边,梯子顶端到地的距离线段对应为另一个直角边,所以梯子顶端到地的距离为252﹣72=242,所以梯子顶端到地为24米;
(2)求出BB'的长度即可;
(3)先求出梯子能够到达墙面的最大高度,再与24.3比较即可.
【解答】解:(1)在Rt△ACB中,
∴AC24m,
答:这架云梯顶端距地面的距离AC有24m.
(2)云梯的底部B在水平方向滑动到B′的距离BB′不是4m.理由如下:
由(1)可知AC=24m,
∴A′C=AC﹣AA′=24﹣4=20m.
在Rt△A′CB′中,
∴,
∴BB′=CB′﹣BC=15﹣7=8m.
(3)若云梯底端离墙的距离刚好为云梯长度的,
则能够到达墙面的最大高度为.
∵24.32=590.49<600,
∴,
∴在相对安全的前提下,云梯的顶端能到达24.3m高的墙头去救援被困人员.
【点评】本题考查勾股定理和解直角三角形,熟练掌握勾股定理是解题关键.
15.(2024 海淀区校级模拟)如图,在△ABC中,AB=AC,AD为BC边上的中线,点E为AD中点,过点A作AF∥BC,交BE的延长线于点F,连接CF.
(1)求证:四边形ADCF为矩形;
(2)若BC=6,sin,求EF的长.
【考点】解直角三角形;等腰三角形的性质;矩形的判定与性质.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;解直角三角形及其应用;运算能力;推理能力.
【答案】见试题解答内容
【分析】(1)先证△AFE≌△DBE(AAS),得出AF=BD,则AF=DC,得出四边形ADCF为平行四边形,再证∠ADC=90°,即可得出结论;
(2)BC=6,AD为BC边上的中线,则,在Rt△ABD 中,,求出,则,又根据点E为AD中点,求出,则EF可根据勾股定理可求.
【解答】(1)证明:∵AD是BC边上的中线,
∴BD=CD,
∵点E是AD的中点,
∴AE=ED,
∵AF∥BC,
∴∠AFE=∠DBE,∠FAE=∠BDE,
在△AFE和△DBE中,
,
∴△AFE≌△DBE(AAS),
∴AF=BD,
∴AF=DC,
又∵AF∥BC,
∴四边形ADCF为平行四边形,
∵AB=AC,AD为BC边上的中线,
∴AD⊥BC,
∴∠ADC=90°,
∴四边形ADCF为矩形;
(2)解:∵BC=6,AD为BC边上的中线,
∴,
∵在Rt△ABD 中,,
∴,
∴,
又∵点E为AD中点,
∴,
∴在 Rt△EBD中,,
∴.
【点评】本题考查了平行四边形的判定、矩形的判定与性质、全等三角形的判定与性质、勾股定理、等腰三角形的性质、锐角三角函数定义等知识;熟练掌握全等三角形的判定与性质和勾股定理是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
