第11章 整式的乘除(预习衔接.夯实基础.含解析)-2025-2026学年八年级上册数学华东师大版(2024)
文档属性
| 名称 | 第11章 整式的乘除(预习衔接.夯实基础.含解析)-2025-2026学年八年级上册数学华东师大版(2024) |

|
|
| 格式 | docx | ||
| 文件大小 | 63.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
预习衔接.夯实基础 整式的乘除
一.选择题(共5小题)
1.(2024秋 长宁区校级期中)下列等式中,哪些从左到右的变形是因式分解( )
A.(x+y)(x﹣2y)=x2﹣xy﹣2y2
B.
C.3x2﹣5x﹣2=(3x+1)(x﹣2)
D.3x2+6x+4=3(x+1)2+1
2.(2024秋 晋安区期中)下列计算正确的是( )
A.a2+a3=a5 B.a2 a3=a5
C.(a2)3=a5 D.(﹣a3)2=﹣a6
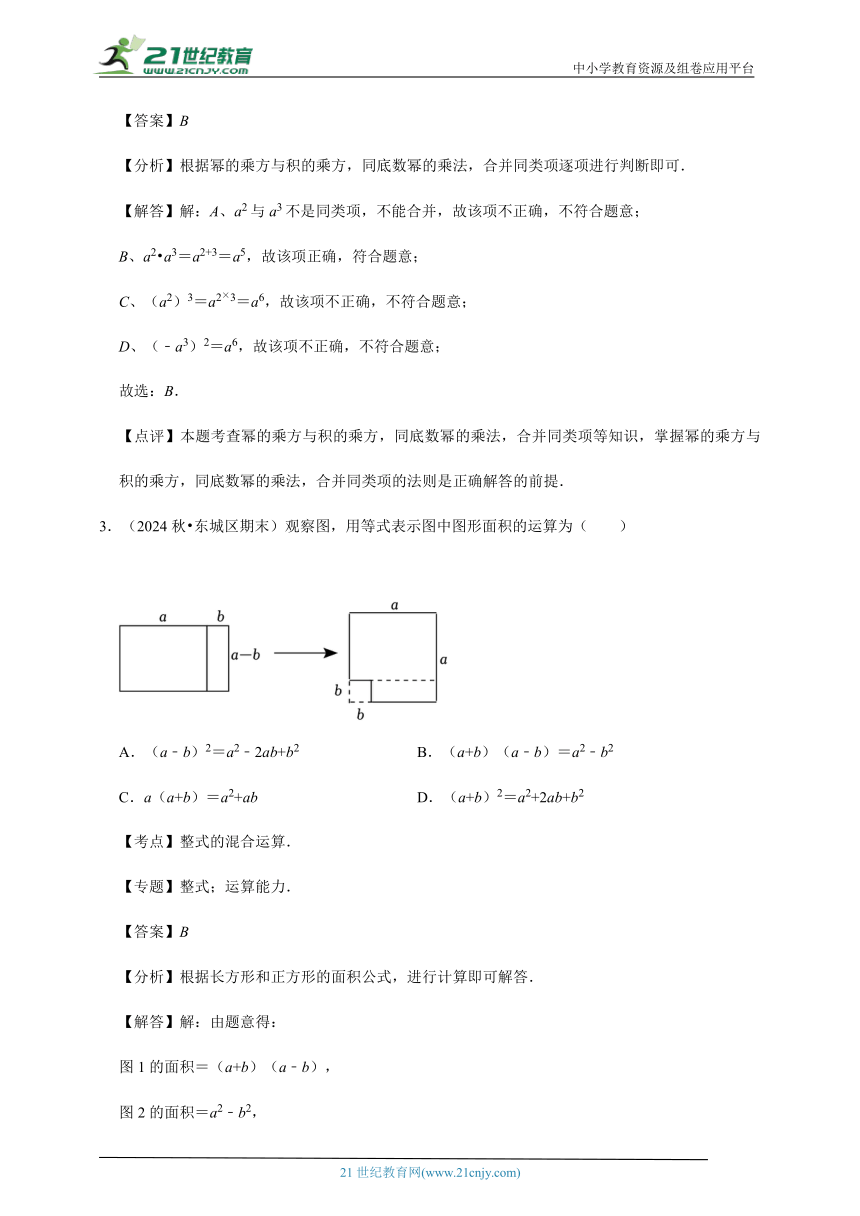
3.(2024秋 东城区期末)观察图,用等式表示图中图形面积的运算为( )
A.(a﹣b)2=a2﹣2ab+b2 B.(a+b)(a﹣b)=a2﹣b2
C.a(a+b)=a2+ab D.(a+b)2=a2+2ab+b2
4.(2024秋 西山区校级期中)计算( )
A.1 B.﹣2 C. D.
5.(2024秋 龙华区校级期中)若(2x﹣3)(x+2)=2x2+mx+n,则m与n的值分别是( )
A.﹣1,6 B.1,﹣6 C.﹣3,﹣2 D.﹣3,2
二.填空题(共5小题)
6.(2024秋 长宁区校级期中)因式分解:ax2y+axy2﹣axy= .
7.(2024春 惠山区期中)如果x2+mx+16完全平方式,则m的值等于 .
8.(2024秋 长宁区校级期中)计算: .
9.(2024秋 香坊区校级期中)已知x2+y2=10,xy=3,则(x+y)2= .
10.(2024秋 南岗区校级期中)已知:a+b=3,ab=5,则a2+b2﹣2a﹣2b+6= .
三.解答题(共5小题)
11.(2024秋 五华区校级期中)分解因式:
(1)xy3﹣xy;
(2)2(x﹣y)﹣4b(x﹣y).
12.(2024秋 东湖区校级期中)先化简,再求值:(2x+1)2﹣x(x﹣1)+(x+2)(x﹣2),其中x=1.
13.(2024秋 西山区校级期中)小红准备计算题目:(x2▅x+2)(x2﹣x),发现第一个因式的一次项系数被墨水遮挡住了,已知这个题目的正确答案是不含三次项的,请计算求出原题中被遮住的一次项系数.
14.(2024秋 徐汇区校级期中)阅读理解
(1)已知下列结果,填空:
(1+a)(1﹣a)=1﹣a2
(1+a)(1﹣a+a2)=1+a3
(1+a)(1﹣a+a2﹣a3)=1﹣a4
(1+a)(1﹣a+a2﹣a3+a4)=1+a5
…
(1+a)(1﹣a+a2﹣a3+…﹣a9)= .
(2)以(1)中最后的结果为参考,求下列代数式的值(结果可以含幂的形式)2﹣22+23﹣24+…+29= .
15.(2024秋 海安市期中)(1)先化简,再求值:(2x﹣3y)(2x+3y)﹣(2x﹣y)2,其中x=3,y=1;
(2)已知x2﹣y2=20,x﹣y=2,求xy的值.
预习衔接.夯实基础 整式的乘除
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 长宁区校级期中)下列等式中,哪些从左到右的变形是因式分解( )
A.(x+y)(x﹣2y)=x2﹣xy﹣2y2
B.
C.3x2﹣5x﹣2=(3x+1)(x﹣2)
D.3x2+6x+4=3(x+1)2+1
【考点】因式分解的意义;因式分解﹣十字相乘法等.
【专题】整式;运算能力.
【答案】C
【分析】根据因式分解的定义“将多项式化为几个整式的积的形式”,由此即可求解.
【解答】解:A.(x+y)(x﹣2y)=x2﹣xy﹣2y2,是整数的乘法,不是因式分解,不符合题意;
B.该式子等号右边不几个整式的积的形式,不是因式分解,不符合题意;
C.3x2﹣5x﹣2=(3x+1)(x﹣2),是因式分解,符合题意;
D.3x2+6x+4=3(x+1)2+1,等号右边不几个整式的积的形式,不是因式分解,不符合题意;
故选:C.
【点评】本题主要考查因式分解的概念,掌握其概念是解题的关键.
2.(2024秋 晋安区期中)下列计算正确的是( )
A.a2+a3=a5 B.a2 a3=a5
C.(a2)3=a5 D.(﹣a3)2=﹣a6
【考点】幂的乘方与积的乘方;合并同类项;同底数幂的乘法.
【专题】整式;运算能力.
【答案】B
【分析】根据幂的乘方与积的乘方,同底数幂的乘法,合并同类项逐项进行判断即可.
【解答】解:A、a2与a3不是同类项,不能合并,故该项不正确,不符合题意;
B、a2 a3=a2+3=a5,故该项正确,符合题意;
C、(a2)3=a2×3=a6,故该项不正确,不符合题意;
D、(﹣a3)2=a6,故该项不正确,不符合题意;
故选:B.
【点评】本题考查幂的乘方与积的乘方,同底数幂的乘法,合并同类项等知识,掌握幂的乘方与积的乘方,同底数幂的乘法,合并同类项的法则是正确解答的前提.
3.(2024秋 东城区期末)观察图,用等式表示图中图形面积的运算为( )
A.(a﹣b)2=a2﹣2ab+b2 B.(a+b)(a﹣b)=a2﹣b2
C.a(a+b)=a2+ab D.(a+b)2=a2+2ab+b2
【考点】整式的混合运算.
【专题】整式;运算能力.
【答案】B
【分析】根据长方形和正方形的面积公式,进行计算即可解答.
【解答】解:由题意得:
图1的面积=(a+b)(a﹣b),
图2的面积=a2﹣b2,
∴(a+b)(a﹣b)=a2﹣b2,
故选:B.
【点评】本题考查了整式的混合运算,熟练掌握长方形和正方形的面积公式是解题的关键.
4.(2024秋 西山区校级期中)计算( )
A.1 B.﹣2 C. D.
【考点】幂的乘方与积的乘方.
【专题】整式;运算能力.
【答案】A
【分析】根据幂的乘方与积的乘方法则进行解题即可.
【解答】解:原式=()2024×22024
=(2)2024
=12024
=1.
故选:A.
【点评】本题考查幂的乘方与积的乘方,熟练掌握运算法则是解题的关键.
5.(2024秋 龙华区校级期中)若(2x﹣3)(x+2)=2x2+mx+n,则m与n的值分别是( )
A.﹣1,6 B.1,﹣6 C.﹣3,﹣2 D.﹣3,2
【考点】多项式乘多项式.
【专题】整式;运算能力.
【答案】B
【分析】利用多项式乘多项式的法则进行运算,再比较即可求解.
【解答】解:∵(2x﹣3)(x+2)=2x2+mx+n,
∴2x2+x﹣6=2x2+mx+n,
∴m=1,n=﹣6.
故选:B.
【点评】本题主要考查多项式乘多项式,解答的关键是对相应的运算法则的掌握.
二.填空题(共5小题)
6.(2024秋 长宁区校级期中)因式分解:ax2y+axy2﹣axy= axy(x+y﹣1) .
【考点】提公因式法与公式法的综合运用.
【专题】整式;运算能力.
【答案】axy(x+y﹣1).
【分析】利用提公因式法因式分解即可.
【解答】解:原式=axy(x+y﹣1),
故答案为:axy(x+y﹣1).
【点评】本题考查提公因式法因式分解,熟练掌握因式分解的方法是解题的关键.
7.(2024春 惠山区期中)如果x2+mx+16完全平方式,则m的值等于 8或﹣8 .
【考点】完全平方式.
【专题】整式;运算能力.
【答案】8或﹣8.
【分析】根据完全平方式得出mx=±2 x y,再求出答案即可.
【解答】解:∵x2+mx+16完全平方式,
∴mx=±2 x y,
解得:m=8或﹣8.
故答案为:8或﹣8.
【点评】本题考查了完全平方式,能熟记完全平方式(完全平方式有a2+2ab+b2和a2﹣2ab+b2两个)是解此题的关键.
8.(2024秋 长宁区校级期中)计算: 4x4y﹣6x3y2+3x2y3 .
【考点】单项式乘多项式;单项式乘单项式.
【专题】整式;运算能力.
【答案】4x4y﹣6x3y2+3x2y3.
【分析】根据单项式乘多项式、单项式乘单项式的运算法则计算即可.
【解答】解:
=4x4y﹣6x3y2+3x2y3,
故答案为:4x4y﹣6x3y2+3x2y3.
【点评】本题考查了单项式乘多项式、单项式乘单项式,熟练掌握运算法则是解题的关键.
9.(2024秋 香坊区校级期中)已知x2+y2=10,xy=3,则(x+y)2= 16 .
【考点】完全平方公式.
【专题】整式;运算能力.
【答案】16.
【分析】利用完全平方公式计算即可.
【解答】解:∵x2+y2=10,xy=3,
∴(x+y)2=x2+2xy+y2=10+2×3=16,
故答案为:16.
【点评】此题考查了完全平方公式,(a+b)2=a2+2ab+b2,熟记公式是解题的关键.
10.(2024秋 南岗区校级期中)已知:a+b=3,ab=5,则a2+b2﹣2a﹣2b+6= ﹣1 .
【考点】完全平方公式.
【专题】整式;运算能力.
【答案】﹣1.
【分析】根据完全平方公式可得a2+b2=(a+b)2﹣2ab,再把a+b=3,ab=5代入计算即可.
【解答】解:∵a+b=3,ab=5,
∴a2+b2﹣2a﹣2b+6
=(a+b)2﹣2ab﹣2(a+b)+6
=32﹣2×5﹣2×3+6
=9﹣10﹣6+6
=﹣1.
故答案为:﹣1.
【点评】本题主要考查了完全平方公式,熟记公式是解答本题的关键.
三.解答题(共5小题)
11.(2024秋 五华区校级期中)分解因式:
(1)xy3﹣xy;
(2)2(x﹣y)﹣4b(x﹣y).
【考点】提公因式法与公式法的综合运用.
【专题】因式分解;运算能力.
【答案】(1)xy(y+1)(y﹣1);
(2)2(x﹣y)(1﹣2b).
【分析】(1)先提公因式,然后利用平方差公式分解因式即可;
(2)利用提公因式法分解因式即可.
【解答】解:(1)xy3﹣xy
=xy(y2﹣1)
=xy(y+1)(y﹣1);
(2)2(x﹣y)﹣4b(x﹣y)=2(x﹣y)(1﹣2b).
【点评】本题考查了因式分解,熟练掌握提公因式法、公式法分解因式是解题的关键.
12.(2024秋 东湖区校级期中)先化简,再求值:(2x+1)2﹣x(x﹣1)+(x+2)(x﹣2),其中x=1.
【考点】整式的混合运算—化简求值.
【专题】实数;运算能力.
【答案】4x2+5x﹣3,6.
【分析】根据完全平方公式、单项式乘多项式和平方差公式将题目中的式子展开,然后合并同类项,再将x的值代入化简后的式子计算即可.
【解答】解:(2x+1)2﹣x(x﹣1)+(x+2)(x﹣2)
=4x2+4x+1﹣x2+x+x2﹣4
=4x2+5x﹣3,
当x=1时,原式=4×12+5×1﹣3=6.
【点评】本题考查了整式的混合运算—化简求值,熟练掌握运算法则是解此题的关键.
13.(2024秋 西山区校级期中)小红准备计算题目:(x2▅x+2)(x2﹣x),发现第一个因式的一次项系数被墨水遮挡住了,已知这个题目的正确答案是不含三次项的,请计算求出原题中被遮住的一次项系数.
【考点】多项式乘多项式.
【专题】整式;运算能力.
【答案】1.
【分析】设一次项系数为m,然后根据多项式乘多项式的运算法则计算,再根据正确答案不含三次项得出m﹣1=0,即可求出m的值.
【解答】解:设一次项系数为m,
(x2+mx+2)(x2﹣x)
=x4﹣x3+mx3﹣mx2+2x2﹣2x
=x4+(m﹣1)x3+(2﹣m)x2﹣2x,
∵正确答案不含三次项,
∴m﹣1=0,
∴m=1.
【点评】本题考查了多项式乘多项式,熟练掌握运算法则是解题的关键.
14.(2024秋 徐汇区校级期中)阅读理解
(1)已知下列结果,填空:
(1+a)(1﹣a)=1﹣a2
(1+a)(1﹣a+a2)=1+a3
(1+a)(1﹣a+a2﹣a3)=1﹣a4
(1+a)(1﹣a+a2﹣a3+a4)=1+a5
…
(1+a)(1﹣a+a2﹣a3+…﹣a9)= 1﹣a10 .
(2)以(1)中最后的结果为参考,求下列代数式的值(结果可以含幂的形式)2﹣22+23﹣24+…+29= .
【考点】平方差公式;规律型:数字的变化类.
【专题】整式;运算能力.
【答案】(1)1﹣a10;
(2).
【分析】(1)仔细观察几个算式从中找到每一个算式的规律,即可得出结果;
(2)利用上述规律计算结果并保留幂的形式即可得到答案.
【解答】解:(1)(1+a)(1﹣a)=1﹣a2
(1+a)(1﹣a+a2)=1+a3
(1+a)(1﹣a+a2﹣a3)=1﹣a4
(1+a)(1﹣a+a2﹣a3+a4)=1+a5
…
(1+a)(1﹣a+a2﹣a3+…﹣a9)=1﹣a10,
故答案为:1﹣a10;
(2)原式=2(1﹣2+22﹣23+24+…+28)
(1+2)×(1﹣2+22﹣23+24+…+28)
.
故答案为:.
【点评】本题考查了数字的变化类题目,解决此类题目的关键是认真观察题目提供的算式,然后从中整理出规律,并利用此规律解题.
15.(2024秋 海安市期中)(1)先化简,再求值:(2x﹣3y)(2x+3y)﹣(2x﹣y)2,其中x=3,y=1;
(2)已知x2﹣y2=20,x﹣y=2,求xy的值.
【考点】整式的混合运算—化简求值.
【专题】计算题;整式;运算能力.
【答案】(1)4xy﹣10y2,2;
(2)24.
【分析】(1)先根据完全平方公式和平方差公式将式子化简,再代入x=3,y=1,求出值即可;
(2)根据平方差公式可求出x+y=10,再求出x和y的值,再代入计算即可.
【解答】解:(1)原式=4x2﹣9y2﹣4x2+4xy﹣y2
=4xy﹣10y2,
将x=3,y=1代入得,
原式=4×3×1﹣10×12=12﹣10=2;
(2)∵x2﹣y2=20,
∴(x+y)(x﹣y)=20,
∵x﹣y=2,
∴x+y=10,
∴x=6,y=4,
∴xy=6×4=24.
【点评】此题主要考查了整式的混合运算—化简求值,掌握平方差公式和完全平方公式将式子进行化简是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.夯实基础 整式的乘除
一.选择题(共5小题)
1.(2024秋 长宁区校级期中)下列等式中,哪些从左到右的变形是因式分解( )
A.(x+y)(x﹣2y)=x2﹣xy﹣2y2
B.
C.3x2﹣5x﹣2=(3x+1)(x﹣2)
D.3x2+6x+4=3(x+1)2+1
2.(2024秋 晋安区期中)下列计算正确的是( )
A.a2+a3=a5 B.a2 a3=a5
C.(a2)3=a5 D.(﹣a3)2=﹣a6
3.(2024秋 东城区期末)观察图,用等式表示图中图形面积的运算为( )
A.(a﹣b)2=a2﹣2ab+b2 B.(a+b)(a﹣b)=a2﹣b2
C.a(a+b)=a2+ab D.(a+b)2=a2+2ab+b2
4.(2024秋 西山区校级期中)计算( )
A.1 B.﹣2 C. D.
5.(2024秋 龙华区校级期中)若(2x﹣3)(x+2)=2x2+mx+n,则m与n的值分别是( )
A.﹣1,6 B.1,﹣6 C.﹣3,﹣2 D.﹣3,2
二.填空题(共5小题)
6.(2024秋 长宁区校级期中)因式分解:ax2y+axy2﹣axy= .
7.(2024春 惠山区期中)如果x2+mx+16完全平方式,则m的值等于 .
8.(2024秋 长宁区校级期中)计算: .
9.(2024秋 香坊区校级期中)已知x2+y2=10,xy=3,则(x+y)2= .
10.(2024秋 南岗区校级期中)已知:a+b=3,ab=5,则a2+b2﹣2a﹣2b+6= .
三.解答题(共5小题)
11.(2024秋 五华区校级期中)分解因式:
(1)xy3﹣xy;
(2)2(x﹣y)﹣4b(x﹣y).
12.(2024秋 东湖区校级期中)先化简,再求值:(2x+1)2﹣x(x﹣1)+(x+2)(x﹣2),其中x=1.
13.(2024秋 西山区校级期中)小红准备计算题目:(x2▅x+2)(x2﹣x),发现第一个因式的一次项系数被墨水遮挡住了,已知这个题目的正确答案是不含三次项的,请计算求出原题中被遮住的一次项系数.
14.(2024秋 徐汇区校级期中)阅读理解
(1)已知下列结果,填空:
(1+a)(1﹣a)=1﹣a2
(1+a)(1﹣a+a2)=1+a3
(1+a)(1﹣a+a2﹣a3)=1﹣a4
(1+a)(1﹣a+a2﹣a3+a4)=1+a5
…
(1+a)(1﹣a+a2﹣a3+…﹣a9)= .
(2)以(1)中最后的结果为参考,求下列代数式的值(结果可以含幂的形式)2﹣22+23﹣24+…+29= .
15.(2024秋 海安市期中)(1)先化简,再求值:(2x﹣3y)(2x+3y)﹣(2x﹣y)2,其中x=3,y=1;
(2)已知x2﹣y2=20,x﹣y=2,求xy的值.
预习衔接.夯实基础 整式的乘除
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 长宁区校级期中)下列等式中,哪些从左到右的变形是因式分解( )
A.(x+y)(x﹣2y)=x2﹣xy﹣2y2
B.
C.3x2﹣5x﹣2=(3x+1)(x﹣2)
D.3x2+6x+4=3(x+1)2+1
【考点】因式分解的意义;因式分解﹣十字相乘法等.
【专题】整式;运算能力.
【答案】C
【分析】根据因式分解的定义“将多项式化为几个整式的积的形式”,由此即可求解.
【解答】解:A.(x+y)(x﹣2y)=x2﹣xy﹣2y2,是整数的乘法,不是因式分解,不符合题意;
B.该式子等号右边不几个整式的积的形式,不是因式分解,不符合题意;
C.3x2﹣5x﹣2=(3x+1)(x﹣2),是因式分解,符合题意;
D.3x2+6x+4=3(x+1)2+1,等号右边不几个整式的积的形式,不是因式分解,不符合题意;
故选:C.
【点评】本题主要考查因式分解的概念,掌握其概念是解题的关键.
2.(2024秋 晋安区期中)下列计算正确的是( )
A.a2+a3=a5 B.a2 a3=a5
C.(a2)3=a5 D.(﹣a3)2=﹣a6
【考点】幂的乘方与积的乘方;合并同类项;同底数幂的乘法.
【专题】整式;运算能力.
【答案】B
【分析】根据幂的乘方与积的乘方,同底数幂的乘法,合并同类项逐项进行判断即可.
【解答】解:A、a2与a3不是同类项,不能合并,故该项不正确,不符合题意;
B、a2 a3=a2+3=a5,故该项正确,符合题意;
C、(a2)3=a2×3=a6,故该项不正确,不符合题意;
D、(﹣a3)2=a6,故该项不正确,不符合题意;
故选:B.
【点评】本题考查幂的乘方与积的乘方,同底数幂的乘法,合并同类项等知识,掌握幂的乘方与积的乘方,同底数幂的乘法,合并同类项的法则是正确解答的前提.
3.(2024秋 东城区期末)观察图,用等式表示图中图形面积的运算为( )
A.(a﹣b)2=a2﹣2ab+b2 B.(a+b)(a﹣b)=a2﹣b2
C.a(a+b)=a2+ab D.(a+b)2=a2+2ab+b2
【考点】整式的混合运算.
【专题】整式;运算能力.
【答案】B
【分析】根据长方形和正方形的面积公式,进行计算即可解答.
【解答】解:由题意得:
图1的面积=(a+b)(a﹣b),
图2的面积=a2﹣b2,
∴(a+b)(a﹣b)=a2﹣b2,
故选:B.
【点评】本题考查了整式的混合运算,熟练掌握长方形和正方形的面积公式是解题的关键.
4.(2024秋 西山区校级期中)计算( )
A.1 B.﹣2 C. D.
【考点】幂的乘方与积的乘方.
【专题】整式;运算能力.
【答案】A
【分析】根据幂的乘方与积的乘方法则进行解题即可.
【解答】解:原式=()2024×22024
=(2)2024
=12024
=1.
故选:A.
【点评】本题考查幂的乘方与积的乘方,熟练掌握运算法则是解题的关键.
5.(2024秋 龙华区校级期中)若(2x﹣3)(x+2)=2x2+mx+n,则m与n的值分别是( )
A.﹣1,6 B.1,﹣6 C.﹣3,﹣2 D.﹣3,2
【考点】多项式乘多项式.
【专题】整式;运算能力.
【答案】B
【分析】利用多项式乘多项式的法则进行运算,再比较即可求解.
【解答】解:∵(2x﹣3)(x+2)=2x2+mx+n,
∴2x2+x﹣6=2x2+mx+n,
∴m=1,n=﹣6.
故选:B.
【点评】本题主要考查多项式乘多项式,解答的关键是对相应的运算法则的掌握.
二.填空题(共5小题)
6.(2024秋 长宁区校级期中)因式分解:ax2y+axy2﹣axy= axy(x+y﹣1) .
【考点】提公因式法与公式法的综合运用.
【专题】整式;运算能力.
【答案】axy(x+y﹣1).
【分析】利用提公因式法因式分解即可.
【解答】解:原式=axy(x+y﹣1),
故答案为:axy(x+y﹣1).
【点评】本题考查提公因式法因式分解,熟练掌握因式分解的方法是解题的关键.
7.(2024春 惠山区期中)如果x2+mx+16完全平方式,则m的值等于 8或﹣8 .
【考点】完全平方式.
【专题】整式;运算能力.
【答案】8或﹣8.
【分析】根据完全平方式得出mx=±2 x y,再求出答案即可.
【解答】解:∵x2+mx+16完全平方式,
∴mx=±2 x y,
解得:m=8或﹣8.
故答案为:8或﹣8.
【点评】本题考查了完全平方式,能熟记完全平方式(完全平方式有a2+2ab+b2和a2﹣2ab+b2两个)是解此题的关键.
8.(2024秋 长宁区校级期中)计算: 4x4y﹣6x3y2+3x2y3 .
【考点】单项式乘多项式;单项式乘单项式.
【专题】整式;运算能力.
【答案】4x4y﹣6x3y2+3x2y3.
【分析】根据单项式乘多项式、单项式乘单项式的运算法则计算即可.
【解答】解:
=4x4y﹣6x3y2+3x2y3,
故答案为:4x4y﹣6x3y2+3x2y3.
【点评】本题考查了单项式乘多项式、单项式乘单项式,熟练掌握运算法则是解题的关键.
9.(2024秋 香坊区校级期中)已知x2+y2=10,xy=3,则(x+y)2= 16 .
【考点】完全平方公式.
【专题】整式;运算能力.
【答案】16.
【分析】利用完全平方公式计算即可.
【解答】解:∵x2+y2=10,xy=3,
∴(x+y)2=x2+2xy+y2=10+2×3=16,
故答案为:16.
【点评】此题考查了完全平方公式,(a+b)2=a2+2ab+b2,熟记公式是解题的关键.
10.(2024秋 南岗区校级期中)已知:a+b=3,ab=5,则a2+b2﹣2a﹣2b+6= ﹣1 .
【考点】完全平方公式.
【专题】整式;运算能力.
【答案】﹣1.
【分析】根据完全平方公式可得a2+b2=(a+b)2﹣2ab,再把a+b=3,ab=5代入计算即可.
【解答】解:∵a+b=3,ab=5,
∴a2+b2﹣2a﹣2b+6
=(a+b)2﹣2ab﹣2(a+b)+6
=32﹣2×5﹣2×3+6
=9﹣10﹣6+6
=﹣1.
故答案为:﹣1.
【点评】本题主要考查了完全平方公式,熟记公式是解答本题的关键.
三.解答题(共5小题)
11.(2024秋 五华区校级期中)分解因式:
(1)xy3﹣xy;
(2)2(x﹣y)﹣4b(x﹣y).
【考点】提公因式法与公式法的综合运用.
【专题】因式分解;运算能力.
【答案】(1)xy(y+1)(y﹣1);
(2)2(x﹣y)(1﹣2b).
【分析】(1)先提公因式,然后利用平方差公式分解因式即可;
(2)利用提公因式法分解因式即可.
【解答】解:(1)xy3﹣xy
=xy(y2﹣1)
=xy(y+1)(y﹣1);
(2)2(x﹣y)﹣4b(x﹣y)=2(x﹣y)(1﹣2b).
【点评】本题考查了因式分解,熟练掌握提公因式法、公式法分解因式是解题的关键.
12.(2024秋 东湖区校级期中)先化简,再求值:(2x+1)2﹣x(x﹣1)+(x+2)(x﹣2),其中x=1.
【考点】整式的混合运算—化简求值.
【专题】实数;运算能力.
【答案】4x2+5x﹣3,6.
【分析】根据完全平方公式、单项式乘多项式和平方差公式将题目中的式子展开,然后合并同类项,再将x的值代入化简后的式子计算即可.
【解答】解:(2x+1)2﹣x(x﹣1)+(x+2)(x﹣2)
=4x2+4x+1﹣x2+x+x2﹣4
=4x2+5x﹣3,
当x=1时,原式=4×12+5×1﹣3=6.
【点评】本题考查了整式的混合运算—化简求值,熟练掌握运算法则是解此题的关键.
13.(2024秋 西山区校级期中)小红准备计算题目:(x2▅x+2)(x2﹣x),发现第一个因式的一次项系数被墨水遮挡住了,已知这个题目的正确答案是不含三次项的,请计算求出原题中被遮住的一次项系数.
【考点】多项式乘多项式.
【专题】整式;运算能力.
【答案】1.
【分析】设一次项系数为m,然后根据多项式乘多项式的运算法则计算,再根据正确答案不含三次项得出m﹣1=0,即可求出m的值.
【解答】解:设一次项系数为m,
(x2+mx+2)(x2﹣x)
=x4﹣x3+mx3﹣mx2+2x2﹣2x
=x4+(m﹣1)x3+(2﹣m)x2﹣2x,
∵正确答案不含三次项,
∴m﹣1=0,
∴m=1.
【点评】本题考查了多项式乘多项式,熟练掌握运算法则是解题的关键.
14.(2024秋 徐汇区校级期中)阅读理解
(1)已知下列结果,填空:
(1+a)(1﹣a)=1﹣a2
(1+a)(1﹣a+a2)=1+a3
(1+a)(1﹣a+a2﹣a3)=1﹣a4
(1+a)(1﹣a+a2﹣a3+a4)=1+a5
…
(1+a)(1﹣a+a2﹣a3+…﹣a9)= 1﹣a10 .
(2)以(1)中最后的结果为参考,求下列代数式的值(结果可以含幂的形式)2﹣22+23﹣24+…+29= .
【考点】平方差公式;规律型:数字的变化类.
【专题】整式;运算能力.
【答案】(1)1﹣a10;
(2).
【分析】(1)仔细观察几个算式从中找到每一个算式的规律,即可得出结果;
(2)利用上述规律计算结果并保留幂的形式即可得到答案.
【解答】解:(1)(1+a)(1﹣a)=1﹣a2
(1+a)(1﹣a+a2)=1+a3
(1+a)(1﹣a+a2﹣a3)=1﹣a4
(1+a)(1﹣a+a2﹣a3+a4)=1+a5
…
(1+a)(1﹣a+a2﹣a3+…﹣a9)=1﹣a10,
故答案为:1﹣a10;
(2)原式=2(1﹣2+22﹣23+24+…+28)
(1+2)×(1﹣2+22﹣23+24+…+28)
.
故答案为:.
【点评】本题考查了数字的变化类题目,解决此类题目的关键是认真观察题目提供的算式,然后从中整理出规律,并利用此规律解题.
15.(2024秋 海安市期中)(1)先化简,再求值:(2x﹣3y)(2x+3y)﹣(2x﹣y)2,其中x=3,y=1;
(2)已知x2﹣y2=20,x﹣y=2,求xy的值.
【考点】整式的混合运算—化简求值.
【专题】计算题;整式;运算能力.
【答案】(1)4xy﹣10y2,2;
(2)24.
【分析】(1)先根据完全平方公式和平方差公式将式子化简,再代入x=3,y=1,求出值即可;
(2)根据平方差公式可求出x+y=10,再求出x和y的值,再代入计算即可.
【解答】解:(1)原式=4x2﹣9y2﹣4x2+4xy﹣y2
=4xy﹣10y2,
将x=3,y=1代入得,
原式=4×3×1﹣10×12=12﹣10=2;
(2)∵x2﹣y2=20,
∴(x+y)(x﹣y)=20,
∵x﹣y=2,
∴x+y=10,
∴x=6,y=4,
∴xy=6×4=24.
【点评】此题主要考查了整式的混合运算—化简求值,掌握平方差公式和完全平方公式将式子进行化简是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
