12.4.2线段垂直平分线(预习衔接.夯实基础.含解析)-2025-2026学年八年级上册数学华东师大版(2024)
文档属性
| 名称 | 12.4.2线段垂直平分线(预习衔接.夯实基础.含解析)-2025-2026学年八年级上册数学华东师大版(2024) |

|
|
| 格式 | docx | ||
| 文件大小 | 307.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 21:45:14 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
预习衔接.夯实基础 线段垂直平分线
一.选择题(共5小题)
1.(2024秋 海珠区校级期中)如图,在△ABC中,DE是边AC的垂直平分线,垂足为E,交BC于点D,若AB=6,BC=9,则△ABD的周长是( )
A.13 B.14 C.15 D.16
2.(2024秋 梁溪区校级期中)如图,某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.这所中学应建在( )
A.△ABC的三条中线的交点
B.△ABC三边的垂直平分线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
3.(2024秋 南浔区期末)在△ABC中,∠B=35°,∠C=50°,分别以点A、C为圆心,大于的长为半径画弧,过两弧的交点作直线,交BC于点P,连结AP,则∠BAP的度数是( )
A.35° B.40° C.45° D.50°
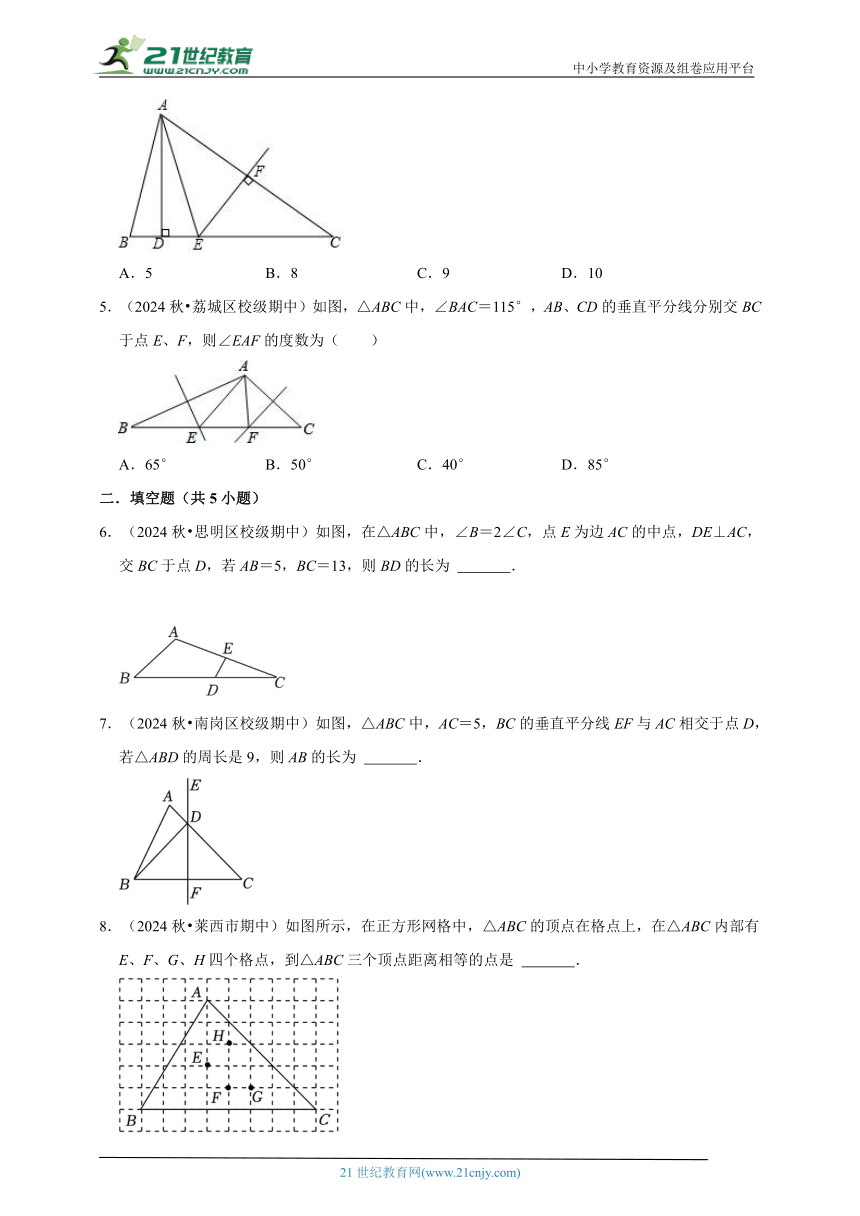
4.(2024春 禅城区期末)如图,△ABC中,AB=AE,且AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,若△ABC周长为16,AC=6,则DC为( )
A.5 B.8 C.9 D.10
5.(2024秋 荔城区校级期中)如图,△ABC中,∠BAC=115°,AB、CD的垂直平分线分别交BC于点E、F,则∠EAF的度数为( )
A.65° B.50° C.40° D.85°
二.填空题(共5小题)
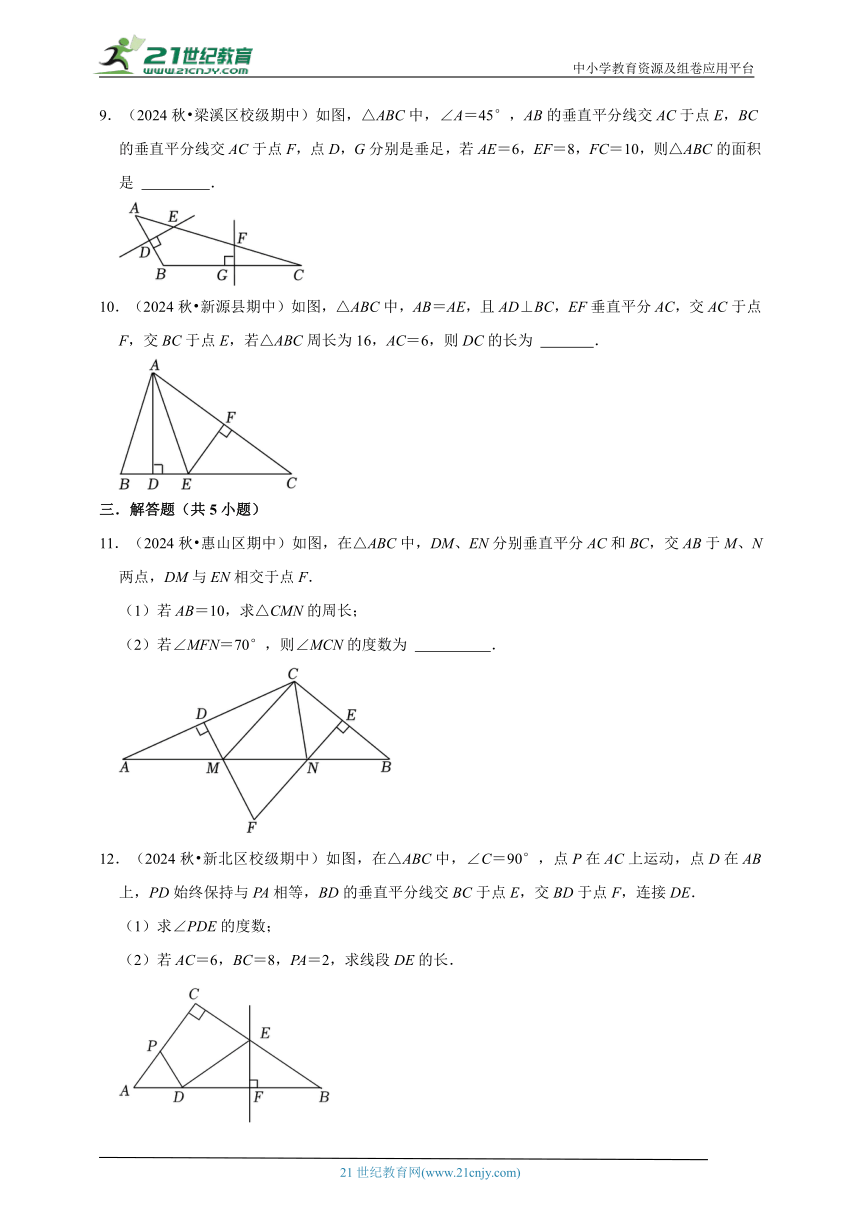
6.(2024秋 思明区校级期中)如图,在△ABC中,∠B=2∠C,点E为边AC的中点,DE⊥AC,交BC于点D,若AB=5,BC=13,则BD的长为 .
7.(2024秋 南岗区校级期中)如图,△ABC中,AC=5,BC的垂直平分线EF与AC相交于点D,若△ABD的周长是9,则AB的长为 .
8.(2024秋 莱西市期中)如图所示,在正方形网格中,△ABC的顶点在格点上,在△ABC内部有E、F、G、H四个格点,到△ABC三个顶点距离相等的点是 .
9.(2024秋 梁溪区校级期中)如图,△ABC中,∠A=45°,AB的垂直平分线交AC于点E,BC的垂直平分线交AC于点F,点D,G分别是垂足,若AE=6,EF=8,FC=10,则△ABC的面积是 .
10.(2024秋 新源县期中)如图,△ABC中,AB=AE,且AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,若△ABC周长为16,AC=6,则DC的长为 .
三.解答题(共5小题)
11.(2024秋 惠山区期中)如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.
(1)若AB=10,求△CMN的周长;
(2)若∠MFN=70°,则∠MCN的度数为 .
12.(2024秋 新北区校级期中)如图,在△ABC中,∠C=90°,点P在AC上运动,点D在AB上,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)求∠PDE的度数;
(2)若AC=6,BC=8,PA=2,求线段DE的长.
13.(2024秋 惠阳区期中)如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.
(1)求证:AB=EC;
(2)若△ABC的周长为20cm,AC=9cm,求DC长.
14.(2024春 新城区校级期末)如图,在△ABC中,EF是边AC的垂直平分线,AB=EC,D是BE的中点,∠BAD=28°,求∠BAC的度数.
15.(2024秋 潍坊期中)如图,在△ABC中,DE,DF分别垂直平分AC和BC,垂足分别为点E、F,DE交AB于点G,DF交AB于点H,连接CG,CH.
(1)若∠ACB=105°,则∠GCH的度数为 ;
(2)若∠GCH=β,求出∠D的度数(用含β的代数式表示);
(3)请在图上连接AD,BD,若△CGH的周长为7cm,△DAB的周长为15cm,求AD的长.
预习衔接.夯实基础 线段垂直平分线
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 海珠区校级期中)如图,在△ABC中,DE是边AC的垂直平分线,垂足为E,交BC于点D,若AB=6,BC=9,则△ABD的周长是( )
A.13 B.14 C.15 D.16
【考点】线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】C
【分析】根据线段垂直平分线的性质可得AD=CD,再根据三角形周长计算公式可推出△ABD的周长=AB+BD+AD=AB+BC,即可求解.
【解答】解:∵DE是边AC的垂直平分线,
∴CD=AD,
∵△ABD的周长=AB+BD+AD,
∴△ABD的周长=AB+BD+CD=AB+BC=6+9=15,
故选:C.
【点评】本题主要考查了线段垂直平分线的性质,熟记“线段垂直平分线上的点到线段两端的距离相等”是解题的关键.
2.(2024秋 梁溪区校级期中)如图,某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.这所中学应建在( )
A.△ABC的三条中线的交点
B.△ABC三边的垂直平分线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
【考点】线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;几何直观.
【答案】B
【分析】根据线段垂直平分线的性质“线段的垂直平分线上的点到线段的两个端点的距离相等”判断即可.
【解答】解:根据线段的垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等,
则学校应建在△ABC三条边的垂直平分线的交点处,
故选:B.
【点评】本题主要考查线段的垂直平分线的性质,解题的关键是熟练掌握线段垂直平分线的性质.
3.(2024秋 南浔区期末)在△ABC中,∠B=35°,∠C=50°,分别以点A、C为圆心,大于的长为半径画弧,过两弧的交点作直线,交BC于点P,连结AP,则∠BAP的度数是( )
A.35° B.40° C.45° D.50°
【考点】线段垂直平分线的性质;三角形内角和定理.
【专题】线段、角、相交线与平行线;几何直观;推理能力.
【答案】C
【分析】根据三角形内角和定理求出∠BAC,根据线段垂直平分线的性质得到PA=PC,进而得出∠PAC=∠C=50°,结合图形计算,得到答案.
【解答】解:在△ABC中,∠B=35°,∠C=50°,
则∠BAC=180°﹣∠B﹣∠C=95°,
根据线段垂直平分线的性质,得PA=PC,
∴∠PAC=∠C=50°,
∴∠BAP=∠BAC﹣∠PAC=95°﹣50°=45°,
故选:C.
【点评】本题考查的是线段垂直平分线的性质、三角形内角和定理、等边对等角,熟练掌握线段垂直平分线的性质是解答本题的关键.
4.(2024春 禅城区期末)如图,△ABC中,AB=AE,且AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,若△ABC周长为16,AC=6,则DC为( )
A.5 B.8 C.9 D.10
【考点】线段垂直平分线的性质.
【专题】三角形;推理能力.
【答案】A
【分析】根据三角形的周长公式求出AB+BC,根据线段垂直平分线的性质得到EA=EC,根据等腰三角形的性质得到BD=DE,结合图形计算,得到答案.
【解答】解:∵△ABC周长为16,
∴AB+BC+AC=16,
∵AC=6,
∴AB+BC=10,
∵EF垂直平分AC,
∴EA=EC,
∵AB=AE,AD⊥BC,
∴BD=DE,
∴AB+BD=AE+DE(AB+BC)=5,
∴DC=DE+EC=AE+DE=5,
故选:A.
【点评】本题考查的是线段垂直平分线的性质、等腰三角形的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
5.(2024秋 荔城区校级期中)如图,△ABC中,∠BAC=115°,AB、CD的垂直平分线分别交BC于点E、F,则∠EAF的度数为( )
A.65° B.50° C.40° D.85°
【考点】线段垂直平分线的性质.
【专题】整体思想;线段、角、相交线与平行线;推理能力.
【答案】B
【分析】利用垂直平分线的性质求EA=EB,则∠B=∠EAG,FA=FC,则∠C=∠FAH,再利用三角形的内角和计算.
【解答】解:∵AB、AC的垂直平分线分别交BC于点E、F,
∴EA=EB,则∠B=∠EAG,
设∠B=∠EAG=x,
∵FA=FC,则∠C=∠FAH,
设∠C=∠FAH=y,
∵∠BAC=115°,
∴x+y+∠EAF=115°,
根据三角形内角和定理,x+y+x+y+∠EAF=180°,
∵x+y=65°,
∴∠EAF=50°.
故选:B.
【点评】此题考查了线段垂直平分线的性质、等腰三角形的判定与性质以及三角形外角的性质.此题难度适中,注意掌握数形结合思想与整体思想的应用.
二.填空题(共5小题)
6.(2024秋 思明区校级期中)如图,在△ABC中,∠B=2∠C,点E为边AC的中点,DE⊥AC,交BC于点D,若AB=5,BC=13,则BD的长为 8 .
【考点】线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】8.
【分析】连接AD,根据线段垂直平分线的性质和等腰三角形的性质即可得到结论.
【解答】解:连接AD,
∵点E为边AC的中点,DE⊥AC,
∴AD=CD,
∴∠DAC=∠C,
∴∠ADB=∠DAC+∠C=2∠C,
∵∠B=2∠C,
∴∠B=∠ADB,
∴AB=AD=5,
∴CD=AD=5,
∴BD=BC﹣CD=8,
故答案为:8.
【点评】本题考查了线段垂直平分线的性质,等腰三角的性质,正确地作出辅助线是解题的关键.
7.(2024秋 南岗区校级期中)如图,△ABC中,AC=5,BC的垂直平分线EF与AC相交于点D,若△ABD的周长是9,则AB的长为 4 .
【考点】线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;运算能力.
【答案】4.
【分析】根据中垂线的性质,可得DC=DB,继而可利用△ABD的周长求出AB+AC即可求解.
【解答】解:∵EF垂直平分BC,
∴DB=DC,
∴△ABD的周长=AB+AD+BD=AB+AD+DC=AB+AC=9.
∵AC=5,
∴AB=9﹣5=4,
故答案为:4.
【点评】本题考查了线段垂直平分线的性质,注意掌握线段垂直平分线上任意一点,到线段两端点的距离相等.
8.(2024秋 莱西市期中)如图所示,在正方形网格中,△ABC的顶点在格点上,在△ABC内部有E、F、G、H四个格点,到△ABC三个顶点距离相等的点是 F .
【考点】线段垂直平分线的性质.
【专题】三角形;推理能力.
【答案】F.
【分析】根据线段的垂直平分线的性质解答即可.
【解答】解:分别作AC、BC的垂直平分线,两直线交于点F,
则点F到△ABC三个顶点距离相等,
故答案为:F.
【点评】本题考查的是线段的垂直平分线的性质,熟记线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
9.(2024秋 梁溪区校级期中)如图,△ABC中,∠A=45°,AB的垂直平分线交AC于点E,BC的垂直平分线交AC于点F,点D,G分别是垂足,若AE=6,EF=8,FC=10,则△ABC的面积是 72 .
【考点】线段垂直平分线的性质;三角形的面积.
【专题】线段、角、相交线与平行线;推理能力.
【答案】72.
【分析】连接BE,首先根据线段垂直平分线的性质,可证得AE=BE=6,再根据等腰三角形的性质及三角形内角和定理,即可证得BE⊥AC,据此即可求得.
【解答】解:如图:连接BE,
∵AB的垂直平分线交AC于点E,
∴AE=BE=6,
∴∠ABE=∠A=45°,
∴∠AEB=180°﹣∠A﹣∠ABE=180°﹣45°﹣45°=90°,
∴BE⊥AC,
∴
=72,
故答案为:72.
【点评】本题考查了线段垂直平分线的性质,三角形内角和定理,证得BE⊥AC是解决本题的关键.
10.(2024秋 新源县期中)如图,△ABC中,AB=AE,且AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,若△ABC周长为16,AC=6,则DC的长为 5 .
【考点】线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】5.
【分析】根据三角形的周长公式求出AB+BC,根据线段垂直平分线的性质可得EA=EC,由等腰三角形的性质可得BD=DE,结合图形,进行计算即可得到答案.
【解答】解:∵△ABC的周长为16,
∴AC+AB+BC=16,
∵AC=6,
∴AB+BC=10,
∵EF垂直平分AC,
∴EA=EC,
∵AD⊥BC,AB=AE,
∴BD=DE,AB=AE=CE,
∴AB+BC=AB+BE+CE=CE+2DE+CE=2CD+2DE=2(CE+DE)=2CD=10,
∴CD=5,
故答案为:5.
【点评】本题主要考查了线段垂直平分线的性质、等腰三角形的性质,熟练掌握线段垂直平分线的性质、等腰三角形的性质是解题的关键.
三.解答题(共5小题)
11.(2024秋 惠山区期中)如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.
(1)若AB=10,求△CMN的周长;
(2)若∠MFN=70°,则∠MCN的度数为 40° .
【考点】线段垂直平分线的性质.
【专题】三角形;推理能力.
【答案】(1)10;
(2)40°.
【分析】(1)根据线段垂直平分线的性质得到MA=MC,NC=NB,再根据三角形周长公式计算即可;
(2)根据三角形内角和定理得到∠FMN+∠FNM=110°,根据对顶角相等、直角三角形的性质求出∠A+∠B,根据等腰三角形的性质计算即可.
【解答】解:(1)∵DM是线段AC的垂直平分线,
∴MA=MC,
∵EN是线段BC的垂直平分线,
∴NC=NB,
∴△CMN的周长=MC+MN+NC=MA+MN+NB=AB=10;
(2)∵∠MFN=70°,
∴∠FMN+∠FNM=180°﹣70°=110°,
∴∠AMD+∠BNE=180°﹣70°=110°,
∵MD⊥AC,NE⊥AB,
∴∠A+∠B=180°﹣110°=70°,
∴∠BAC=180°﹣(∠A+∠B)=180°﹣70°=110°,
∵MA=MC,NC=NB,
∴∠MCA=∠A,∠NCB=∠B,
∴∠MCA+∠NCB=70°,
∴∠MCN=110°﹣70°=40°,
故答案为:40°.
【点评】本题考查的是线段的垂直平分线的性质,熟记线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
12.(2024秋 新北区校级期中)如图,在△ABC中,∠C=90°,点P在AC上运动,点D在AB上,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)求∠PDE的度数;
(2)若AC=6,BC=8,PA=2,求线段DE的长.
【考点】线段垂直平分线的性质.
【专题】等腰三角形与直角三角形;推理能力.
【答案】(1)90°;
(2).
【分析】(1)根据等腰三角形的性质得到∠A=∠PDA,根据三角形的外角性质得到∠CPD=2∠A,根据线段垂直平分线的性质得到ED=EB,得到∠B=∠EDB,得到∠CED=2∠B,根据四边形内角和等于360°计算即可;
(2)根据勾股定理列出方程,解方程得到答案.
【解答】解:(1)在△ABC中,∠C=90°,
则∠A+∠B=90°,
∵PD=PA,
∴∠A=∠PDA,
∴∠CPD=∠A+∠PDA=2∠A,
∵EF是BD的垂直平分线,
∴ED=EB,
∴∠B=∠EDB,
∴∠CED=∠B+∠EDB=2∠B,
∴∠CPD+∠CED=2(∠A+∠B)=180°,
∴∠PDE=360°﹣180°﹣90°=90°;
(2)如图,连接PE,
∵AC=6,PA=2,
∴PC=6﹣2=4,
∵BC=8,
∴CE=8﹣BE=8﹣DE,
则PC2+CE2=PD2+DE2,即42+(8﹣DE)2=22+DE2,
解得:DE.
【点评】本题考查的是线段的垂直平分线的性质,熟记线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
13.(2024秋 惠阳区期中)如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.
(1)求证:AB=EC;
(2)若△ABC的周长为20cm,AC=9cm,求DC长.
【考点】线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】(1)见解析;
(2)DC=5.5cm.
【分析】(1)根据线段垂直平分线的性质得到AE=EC,AB=AE,等量代换证明结论;
(2)根据三角形的周长公式得到AB+BC+AC=20,根据AB=EC,BD=DE计算,得到答案.
【解答】(1)证明:∵EF垂直平分AC,
∴AE=EC,
∵AD⊥BC,BD=DE,
∴AD垂直平分BE,
∴AB=AE,
∴AB=EC;
(2)解:∵△ABC的周长为20cm,
∴AB+BC+AC=20cm,
∵AC=9cm,
∴AB+BC=11cm,
∵AB=EC,BD=DE,
∴
=5.5cm.
【点评】本题考查线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
14.(2024春 新城区校级期末)如图,在△ABC中,EF是边AC的垂直平分线,AB=EC,D是BE的中点,∠BAD=28°,求∠BAC的度数.
【考点】线段垂直平分线的性质;等腰三角形的判定与性质.
【专题】等腰三角形与直角三角形;运算能力.
【答案】见试题解答内容
【分析】连接AE,根据线段垂直平分线的性质可得EA=EC,从而可得∠C=∠EAC,进而可得AB=AE,然后利用等腰三角形的三线合一性质可得∠BAD=∠DAE=28°,∠ADE=90°,从而可得∠AED=62°,再利用三角形的外角性质可得∠C=∠EAC=31°,最后利用角的和差关系进行计算,即可解答.
【解答】解:连接AE,
∵EF是边AC的垂直平分线,
∴EA=EC,
∴∠C=∠EAC,
∵AB=EC,
∴AB=AE,
∵D是BE的中点,
∴∠BAD=∠DAE=28°,∠ADE=90°,
∴∠AED=90°﹣∠EAD=62°,
∵∠AED是△ACE的一个外角,
∴∠AED=∠C+∠EAC=62°,
∴∠C=∠EAC=31°,
∴∠BAC=∠BAD+∠DAE+∠EAC=87°,
∴∠BAC的度数为87°.
【点评】本题考查了等腰三角形的判定与性质,线段垂直平分线的性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
15.(2024秋 潍坊期中)如图,在△ABC中,DE,DF分别垂直平分AC和BC,垂足分别为点E、F,DE交AB于点G,DF交AB于点H,连接CG,CH.
(1)若∠ACB=105°,则∠GCH的度数为 30° ;
(2)若∠GCH=β,求出∠D的度数(用含β的代数式表示);
(3)请在图上连接AD,BD,若△CGH的周长为7cm,△DAB的周长为15cm,求AD的长.
【考点】线段垂直平分线的性质;等腰三角形的性质.
【专题】等腰三角形与直角三角形;推理能力.
【答案】(1)30°;
(2)∴∠D;
(3)AD的长为4cm.
【分析】(1)根据线段垂直平分线的性质得AE=CE,BH=CH,则∠ACG=∠A,∠BCH=∠B,由三角形的内角和定理可得∠A+∠B=75°,根据角的和差即可求解;
(2)由三角形的内角和定理以及三角形外角的性质可得∠A+∠B,求出∠DGH+∠DHG=90°﹣∠A+90°﹣∠B=180°﹣(∠A+∠B)=180°180°﹣∠D,即可得出答案;
(3)根据线段垂直平分线的性质得AD=CD=BD,BH=CH,AG=CG,由△CGH的周长为7cm,可得AB=AG+GH+BH=CG+GH+CH=7cm,由△DAB的周长为15cm即可求解.
【解答】解:(1)∵DE,DF分别垂直平分AC和BC,
∴AE=CE,BH=CH,
∴∠ACG=∠A,∠BCH=∠B,
∵∠A+∠B=180°﹣∠ACB=180°﹣105°=75°,
∴∠ACG+∠BCH=75°,
∴∠GCH=∠ACB﹣(∠ACG+∠BCH)=30°,
故答案为:30°;
(2)∵∠ACG=∠A,∠BCH=∠B,
∴∠CGB=∠A+∠ACG=2∠A,∴∠CHG=∠B+∠BCH=2∠B,
∴∠A+∠B,
∵DE,DF分别垂直平分AC和BC,垂足分别为点E、F,
∴∠AGE=∠DGH=90°﹣∠A,∠BHF=∠DHG=90°﹣∠B,
∴∠DGH+∠DHG=90°﹣∠A+90°﹣∠B=180°﹣(∠A+∠B)=180°180°﹣∠D,
∴∠D;
(3)连接AD,BD,CD,
∵DE,DF分别垂直平分AC和BC,
∴AD=CD=BD,BH=CH,AG=CG,
∵△CGH的周长为7cm,
∴AB=AG+GH+BH=CG+GH+CH=7cm,
∵△DAB的周长为15cm,AD=BD,
∴AD(15﹣7)=4(cm),
∴AD的长为4cm.
【点评】本题考查了等腰三角形的性质,线段垂直平分线的性质,灵活运用这些性质解决问题是本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.夯实基础 线段垂直平分线
一.选择题(共5小题)
1.(2024秋 海珠区校级期中)如图,在△ABC中,DE是边AC的垂直平分线,垂足为E,交BC于点D,若AB=6,BC=9,则△ABD的周长是( )
A.13 B.14 C.15 D.16
2.(2024秋 梁溪区校级期中)如图,某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.这所中学应建在( )
A.△ABC的三条中线的交点
B.△ABC三边的垂直平分线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
3.(2024秋 南浔区期末)在△ABC中,∠B=35°,∠C=50°,分别以点A、C为圆心,大于的长为半径画弧,过两弧的交点作直线,交BC于点P,连结AP,则∠BAP的度数是( )
A.35° B.40° C.45° D.50°
4.(2024春 禅城区期末)如图,△ABC中,AB=AE,且AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,若△ABC周长为16,AC=6,则DC为( )
A.5 B.8 C.9 D.10
5.(2024秋 荔城区校级期中)如图,△ABC中,∠BAC=115°,AB、CD的垂直平分线分别交BC于点E、F,则∠EAF的度数为( )
A.65° B.50° C.40° D.85°
二.填空题(共5小题)
6.(2024秋 思明区校级期中)如图,在△ABC中,∠B=2∠C,点E为边AC的中点,DE⊥AC,交BC于点D,若AB=5,BC=13,则BD的长为 .
7.(2024秋 南岗区校级期中)如图,△ABC中,AC=5,BC的垂直平分线EF与AC相交于点D,若△ABD的周长是9,则AB的长为 .
8.(2024秋 莱西市期中)如图所示,在正方形网格中,△ABC的顶点在格点上,在△ABC内部有E、F、G、H四个格点,到△ABC三个顶点距离相等的点是 .
9.(2024秋 梁溪区校级期中)如图,△ABC中,∠A=45°,AB的垂直平分线交AC于点E,BC的垂直平分线交AC于点F,点D,G分别是垂足,若AE=6,EF=8,FC=10,则△ABC的面积是 .
10.(2024秋 新源县期中)如图,△ABC中,AB=AE,且AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,若△ABC周长为16,AC=6,则DC的长为 .
三.解答题(共5小题)
11.(2024秋 惠山区期中)如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.
(1)若AB=10,求△CMN的周长;
(2)若∠MFN=70°,则∠MCN的度数为 .
12.(2024秋 新北区校级期中)如图,在△ABC中,∠C=90°,点P在AC上运动,点D在AB上,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)求∠PDE的度数;
(2)若AC=6,BC=8,PA=2,求线段DE的长.
13.(2024秋 惠阳区期中)如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.
(1)求证:AB=EC;
(2)若△ABC的周长为20cm,AC=9cm,求DC长.
14.(2024春 新城区校级期末)如图,在△ABC中,EF是边AC的垂直平分线,AB=EC,D是BE的中点,∠BAD=28°,求∠BAC的度数.
15.(2024秋 潍坊期中)如图,在△ABC中,DE,DF分别垂直平分AC和BC,垂足分别为点E、F,DE交AB于点G,DF交AB于点H,连接CG,CH.
(1)若∠ACB=105°,则∠GCH的度数为 ;
(2)若∠GCH=β,求出∠D的度数(用含β的代数式表示);
(3)请在图上连接AD,BD,若△CGH的周长为7cm,△DAB的周长为15cm,求AD的长.
预习衔接.夯实基础 线段垂直平分线
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 海珠区校级期中)如图,在△ABC中,DE是边AC的垂直平分线,垂足为E,交BC于点D,若AB=6,BC=9,则△ABD的周长是( )
A.13 B.14 C.15 D.16
【考点】线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】C
【分析】根据线段垂直平分线的性质可得AD=CD,再根据三角形周长计算公式可推出△ABD的周长=AB+BD+AD=AB+BC,即可求解.
【解答】解:∵DE是边AC的垂直平分线,
∴CD=AD,
∵△ABD的周长=AB+BD+AD,
∴△ABD的周长=AB+BD+CD=AB+BC=6+9=15,
故选:C.
【点评】本题主要考查了线段垂直平分线的性质,熟记“线段垂直平分线上的点到线段两端的距离相等”是解题的关键.
2.(2024秋 梁溪区校级期中)如图,某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.这所中学应建在( )
A.△ABC的三条中线的交点
B.△ABC三边的垂直平分线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
【考点】线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;几何直观.
【答案】B
【分析】根据线段垂直平分线的性质“线段的垂直平分线上的点到线段的两个端点的距离相等”判断即可.
【解答】解:根据线段的垂直平分线的性质:线段的垂直平分线上的点到线段的两个端点的距离相等,
则学校应建在△ABC三条边的垂直平分线的交点处,
故选:B.
【点评】本题主要考查线段的垂直平分线的性质,解题的关键是熟练掌握线段垂直平分线的性质.
3.(2024秋 南浔区期末)在△ABC中,∠B=35°,∠C=50°,分别以点A、C为圆心,大于的长为半径画弧,过两弧的交点作直线,交BC于点P,连结AP,则∠BAP的度数是( )
A.35° B.40° C.45° D.50°
【考点】线段垂直平分线的性质;三角形内角和定理.
【专题】线段、角、相交线与平行线;几何直观;推理能力.
【答案】C
【分析】根据三角形内角和定理求出∠BAC,根据线段垂直平分线的性质得到PA=PC,进而得出∠PAC=∠C=50°,结合图形计算,得到答案.
【解答】解:在△ABC中,∠B=35°,∠C=50°,
则∠BAC=180°﹣∠B﹣∠C=95°,
根据线段垂直平分线的性质,得PA=PC,
∴∠PAC=∠C=50°,
∴∠BAP=∠BAC﹣∠PAC=95°﹣50°=45°,
故选:C.
【点评】本题考查的是线段垂直平分线的性质、三角形内角和定理、等边对等角,熟练掌握线段垂直平分线的性质是解答本题的关键.
4.(2024春 禅城区期末)如图,△ABC中,AB=AE,且AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,若△ABC周长为16,AC=6,则DC为( )
A.5 B.8 C.9 D.10
【考点】线段垂直平分线的性质.
【专题】三角形;推理能力.
【答案】A
【分析】根据三角形的周长公式求出AB+BC,根据线段垂直平分线的性质得到EA=EC,根据等腰三角形的性质得到BD=DE,结合图形计算,得到答案.
【解答】解:∵△ABC周长为16,
∴AB+BC+AC=16,
∵AC=6,
∴AB+BC=10,
∵EF垂直平分AC,
∴EA=EC,
∵AB=AE,AD⊥BC,
∴BD=DE,
∴AB+BD=AE+DE(AB+BC)=5,
∴DC=DE+EC=AE+DE=5,
故选:A.
【点评】本题考查的是线段垂直平分线的性质、等腰三角形的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
5.(2024秋 荔城区校级期中)如图,△ABC中,∠BAC=115°,AB、CD的垂直平分线分别交BC于点E、F,则∠EAF的度数为( )
A.65° B.50° C.40° D.85°
【考点】线段垂直平分线的性质.
【专题】整体思想;线段、角、相交线与平行线;推理能力.
【答案】B
【分析】利用垂直平分线的性质求EA=EB,则∠B=∠EAG,FA=FC,则∠C=∠FAH,再利用三角形的内角和计算.
【解答】解:∵AB、AC的垂直平分线分别交BC于点E、F,
∴EA=EB,则∠B=∠EAG,
设∠B=∠EAG=x,
∵FA=FC,则∠C=∠FAH,
设∠C=∠FAH=y,
∵∠BAC=115°,
∴x+y+∠EAF=115°,
根据三角形内角和定理,x+y+x+y+∠EAF=180°,
∵x+y=65°,
∴∠EAF=50°.
故选:B.
【点评】此题考查了线段垂直平分线的性质、等腰三角形的判定与性质以及三角形外角的性质.此题难度适中,注意掌握数形结合思想与整体思想的应用.
二.填空题(共5小题)
6.(2024秋 思明区校级期中)如图,在△ABC中,∠B=2∠C,点E为边AC的中点,DE⊥AC,交BC于点D,若AB=5,BC=13,则BD的长为 8 .
【考点】线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】8.
【分析】连接AD,根据线段垂直平分线的性质和等腰三角形的性质即可得到结论.
【解答】解:连接AD,
∵点E为边AC的中点,DE⊥AC,
∴AD=CD,
∴∠DAC=∠C,
∴∠ADB=∠DAC+∠C=2∠C,
∵∠B=2∠C,
∴∠B=∠ADB,
∴AB=AD=5,
∴CD=AD=5,
∴BD=BC﹣CD=8,
故答案为:8.
【点评】本题考查了线段垂直平分线的性质,等腰三角的性质,正确地作出辅助线是解题的关键.
7.(2024秋 南岗区校级期中)如图,△ABC中,AC=5,BC的垂直平分线EF与AC相交于点D,若△ABD的周长是9,则AB的长为 4 .
【考点】线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;运算能力.
【答案】4.
【分析】根据中垂线的性质,可得DC=DB,继而可利用△ABD的周长求出AB+AC即可求解.
【解答】解:∵EF垂直平分BC,
∴DB=DC,
∴△ABD的周长=AB+AD+BD=AB+AD+DC=AB+AC=9.
∵AC=5,
∴AB=9﹣5=4,
故答案为:4.
【点评】本题考查了线段垂直平分线的性质,注意掌握线段垂直平分线上任意一点,到线段两端点的距离相等.
8.(2024秋 莱西市期中)如图所示,在正方形网格中,△ABC的顶点在格点上,在△ABC内部有E、F、G、H四个格点,到△ABC三个顶点距离相等的点是 F .
【考点】线段垂直平分线的性质.
【专题】三角形;推理能力.
【答案】F.
【分析】根据线段的垂直平分线的性质解答即可.
【解答】解:分别作AC、BC的垂直平分线,两直线交于点F,
则点F到△ABC三个顶点距离相等,
故答案为:F.
【点评】本题考查的是线段的垂直平分线的性质,熟记线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
9.(2024秋 梁溪区校级期中)如图,△ABC中,∠A=45°,AB的垂直平分线交AC于点E,BC的垂直平分线交AC于点F,点D,G分别是垂足,若AE=6,EF=8,FC=10,则△ABC的面积是 72 .
【考点】线段垂直平分线的性质;三角形的面积.
【专题】线段、角、相交线与平行线;推理能力.
【答案】72.
【分析】连接BE,首先根据线段垂直平分线的性质,可证得AE=BE=6,再根据等腰三角形的性质及三角形内角和定理,即可证得BE⊥AC,据此即可求得.
【解答】解:如图:连接BE,
∵AB的垂直平分线交AC于点E,
∴AE=BE=6,
∴∠ABE=∠A=45°,
∴∠AEB=180°﹣∠A﹣∠ABE=180°﹣45°﹣45°=90°,
∴BE⊥AC,
∴
=72,
故答案为:72.
【点评】本题考查了线段垂直平分线的性质,三角形内角和定理,证得BE⊥AC是解决本题的关键.
10.(2024秋 新源县期中)如图,△ABC中,AB=AE,且AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,若△ABC周长为16,AC=6,则DC的长为 5 .
【考点】线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】5.
【分析】根据三角形的周长公式求出AB+BC,根据线段垂直平分线的性质可得EA=EC,由等腰三角形的性质可得BD=DE,结合图形,进行计算即可得到答案.
【解答】解:∵△ABC的周长为16,
∴AC+AB+BC=16,
∵AC=6,
∴AB+BC=10,
∵EF垂直平分AC,
∴EA=EC,
∵AD⊥BC,AB=AE,
∴BD=DE,AB=AE=CE,
∴AB+BC=AB+BE+CE=CE+2DE+CE=2CD+2DE=2(CE+DE)=2CD=10,
∴CD=5,
故答案为:5.
【点评】本题主要考查了线段垂直平分线的性质、等腰三角形的性质,熟练掌握线段垂直平分线的性质、等腰三角形的性质是解题的关键.
三.解答题(共5小题)
11.(2024秋 惠山区期中)如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.
(1)若AB=10,求△CMN的周长;
(2)若∠MFN=70°,则∠MCN的度数为 40° .
【考点】线段垂直平分线的性质.
【专题】三角形;推理能力.
【答案】(1)10;
(2)40°.
【分析】(1)根据线段垂直平分线的性质得到MA=MC,NC=NB,再根据三角形周长公式计算即可;
(2)根据三角形内角和定理得到∠FMN+∠FNM=110°,根据对顶角相等、直角三角形的性质求出∠A+∠B,根据等腰三角形的性质计算即可.
【解答】解:(1)∵DM是线段AC的垂直平分线,
∴MA=MC,
∵EN是线段BC的垂直平分线,
∴NC=NB,
∴△CMN的周长=MC+MN+NC=MA+MN+NB=AB=10;
(2)∵∠MFN=70°,
∴∠FMN+∠FNM=180°﹣70°=110°,
∴∠AMD+∠BNE=180°﹣70°=110°,
∵MD⊥AC,NE⊥AB,
∴∠A+∠B=180°﹣110°=70°,
∴∠BAC=180°﹣(∠A+∠B)=180°﹣70°=110°,
∵MA=MC,NC=NB,
∴∠MCA=∠A,∠NCB=∠B,
∴∠MCA+∠NCB=70°,
∴∠MCN=110°﹣70°=40°,
故答案为:40°.
【点评】本题考查的是线段的垂直平分线的性质,熟记线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
12.(2024秋 新北区校级期中)如图,在△ABC中,∠C=90°,点P在AC上运动,点D在AB上,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)求∠PDE的度数;
(2)若AC=6,BC=8,PA=2,求线段DE的长.
【考点】线段垂直平分线的性质.
【专题】等腰三角形与直角三角形;推理能力.
【答案】(1)90°;
(2).
【分析】(1)根据等腰三角形的性质得到∠A=∠PDA,根据三角形的外角性质得到∠CPD=2∠A,根据线段垂直平分线的性质得到ED=EB,得到∠B=∠EDB,得到∠CED=2∠B,根据四边形内角和等于360°计算即可;
(2)根据勾股定理列出方程,解方程得到答案.
【解答】解:(1)在△ABC中,∠C=90°,
则∠A+∠B=90°,
∵PD=PA,
∴∠A=∠PDA,
∴∠CPD=∠A+∠PDA=2∠A,
∵EF是BD的垂直平分线,
∴ED=EB,
∴∠B=∠EDB,
∴∠CED=∠B+∠EDB=2∠B,
∴∠CPD+∠CED=2(∠A+∠B)=180°,
∴∠PDE=360°﹣180°﹣90°=90°;
(2)如图,连接PE,
∵AC=6,PA=2,
∴PC=6﹣2=4,
∵BC=8,
∴CE=8﹣BE=8﹣DE,
则PC2+CE2=PD2+DE2,即42+(8﹣DE)2=22+DE2,
解得:DE.
【点评】本题考查的是线段的垂直平分线的性质,熟记线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
13.(2024秋 惠阳区期中)如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.
(1)求证:AB=EC;
(2)若△ABC的周长为20cm,AC=9cm,求DC长.
【考点】线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】(1)见解析;
(2)DC=5.5cm.
【分析】(1)根据线段垂直平分线的性质得到AE=EC,AB=AE,等量代换证明结论;
(2)根据三角形的周长公式得到AB+BC+AC=20,根据AB=EC,BD=DE计算,得到答案.
【解答】(1)证明:∵EF垂直平分AC,
∴AE=EC,
∵AD⊥BC,BD=DE,
∴AD垂直平分BE,
∴AB=AE,
∴AB=EC;
(2)解:∵△ABC的周长为20cm,
∴AB+BC+AC=20cm,
∵AC=9cm,
∴AB+BC=11cm,
∵AB=EC,BD=DE,
∴
=5.5cm.
【点评】本题考查线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
14.(2024春 新城区校级期末)如图,在△ABC中,EF是边AC的垂直平分线,AB=EC,D是BE的中点,∠BAD=28°,求∠BAC的度数.
【考点】线段垂直平分线的性质;等腰三角形的判定与性质.
【专题】等腰三角形与直角三角形;运算能力.
【答案】见试题解答内容
【分析】连接AE,根据线段垂直平分线的性质可得EA=EC,从而可得∠C=∠EAC,进而可得AB=AE,然后利用等腰三角形的三线合一性质可得∠BAD=∠DAE=28°,∠ADE=90°,从而可得∠AED=62°,再利用三角形的外角性质可得∠C=∠EAC=31°,最后利用角的和差关系进行计算,即可解答.
【解答】解:连接AE,
∵EF是边AC的垂直平分线,
∴EA=EC,
∴∠C=∠EAC,
∵AB=EC,
∴AB=AE,
∵D是BE的中点,
∴∠BAD=∠DAE=28°,∠ADE=90°,
∴∠AED=90°﹣∠EAD=62°,
∵∠AED是△ACE的一个外角,
∴∠AED=∠C+∠EAC=62°,
∴∠C=∠EAC=31°,
∴∠BAC=∠BAD+∠DAE+∠EAC=87°,
∴∠BAC的度数为87°.
【点评】本题考查了等腰三角形的判定与性质,线段垂直平分线的性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
15.(2024秋 潍坊期中)如图,在△ABC中,DE,DF分别垂直平分AC和BC,垂足分别为点E、F,DE交AB于点G,DF交AB于点H,连接CG,CH.
(1)若∠ACB=105°,则∠GCH的度数为 30° ;
(2)若∠GCH=β,求出∠D的度数(用含β的代数式表示);
(3)请在图上连接AD,BD,若△CGH的周长为7cm,△DAB的周长为15cm,求AD的长.
【考点】线段垂直平分线的性质;等腰三角形的性质.
【专题】等腰三角形与直角三角形;推理能力.
【答案】(1)30°;
(2)∴∠D;
(3)AD的长为4cm.
【分析】(1)根据线段垂直平分线的性质得AE=CE,BH=CH,则∠ACG=∠A,∠BCH=∠B,由三角形的内角和定理可得∠A+∠B=75°,根据角的和差即可求解;
(2)由三角形的内角和定理以及三角形外角的性质可得∠A+∠B,求出∠DGH+∠DHG=90°﹣∠A+90°﹣∠B=180°﹣(∠A+∠B)=180°180°﹣∠D,即可得出答案;
(3)根据线段垂直平分线的性质得AD=CD=BD,BH=CH,AG=CG,由△CGH的周长为7cm,可得AB=AG+GH+BH=CG+GH+CH=7cm,由△DAB的周长为15cm即可求解.
【解答】解:(1)∵DE,DF分别垂直平分AC和BC,
∴AE=CE,BH=CH,
∴∠ACG=∠A,∠BCH=∠B,
∵∠A+∠B=180°﹣∠ACB=180°﹣105°=75°,
∴∠ACG+∠BCH=75°,
∴∠GCH=∠ACB﹣(∠ACG+∠BCH)=30°,
故答案为:30°;
(2)∵∠ACG=∠A,∠BCH=∠B,
∴∠CGB=∠A+∠ACG=2∠A,∴∠CHG=∠B+∠BCH=2∠B,
∴∠A+∠B,
∵DE,DF分别垂直平分AC和BC,垂足分别为点E、F,
∴∠AGE=∠DGH=90°﹣∠A,∠BHF=∠DHG=90°﹣∠B,
∴∠DGH+∠DHG=90°﹣∠A+90°﹣∠B=180°﹣(∠A+∠B)=180°180°﹣∠D,
∴∠D;
(3)连接AD,BD,CD,
∵DE,DF分别垂直平分AC和BC,
∴AD=CD=BD,BH=CH,AG=CG,
∵△CGH的周长为7cm,
∴AB=AG+GH+BH=CG+GH+CH=7cm,
∵△DAB的周长为15cm,AD=BD,
∴AD(15﹣7)=4(cm),
∴AD的长为4cm.
【点评】本题考查了等腰三角形的性质,线段垂直平分线的性质,灵活运用这些性质解决问题是本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
