12.4.3角平分线(预习衔接.夯实基础.含解析)-2025-2026学年八年级上册数学华东师大版(2024)
文档属性
| 名称 | 12.4.3角平分线(预习衔接.夯实基础.含解析)-2025-2026学年八年级上册数学华东师大版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 738.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 21:34:19 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
预习衔接.夯实基础 角平分线
一.选择题(共5小题)
1.(2024秋 广州期中)如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于B,DF⊥AC于F,△ABC的面积是30,AB=13,AC=7,则DE的长( )
A.3 B.4 C.5 D.6
2.(2024秋 惠阳区期中)如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,S△ABC=8,DE=2,AB=5,则AC长是( )
A.6 B.5 C.4 D.3
3.(2024秋 鹤山市期中)如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=30,BD:CD=3:2,则点D到AB的距离为( )
A.18 B.12 C.15 D.16
4.(2024秋 越秀区校级期中)如图,一把直尺压住射线OB,另一把完全一样的直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的平分线.”他这样做的依据是( )
A.角平分线上的点到这个角两边的距离相等
B.角的内部到角的两边距离相等的点在角的平分线上
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
5.(2024秋 秦淮区期中)如图,△ABC的边AB=10,BC=12,O是△ABC三条角平分线的交点,若△ABO的面积为15,则△BCO的面积为( )
A.11 B.17 C.18 D.20
二.填空题(共5小题)
6.(2024秋 翁源县期中)如图,射线OE是∠AOB的平分线,C是射线OE上一点,CF⊥OA于点F.若D是射线OB上一点,且OD=CF=6,则△ODC的面积是 .
7.(2024秋 新吴区期中)如图,AD是△ABC的角平分线,DE⊥AB于点E,△ADC的面积=9,DE=2,则AC的长是 .
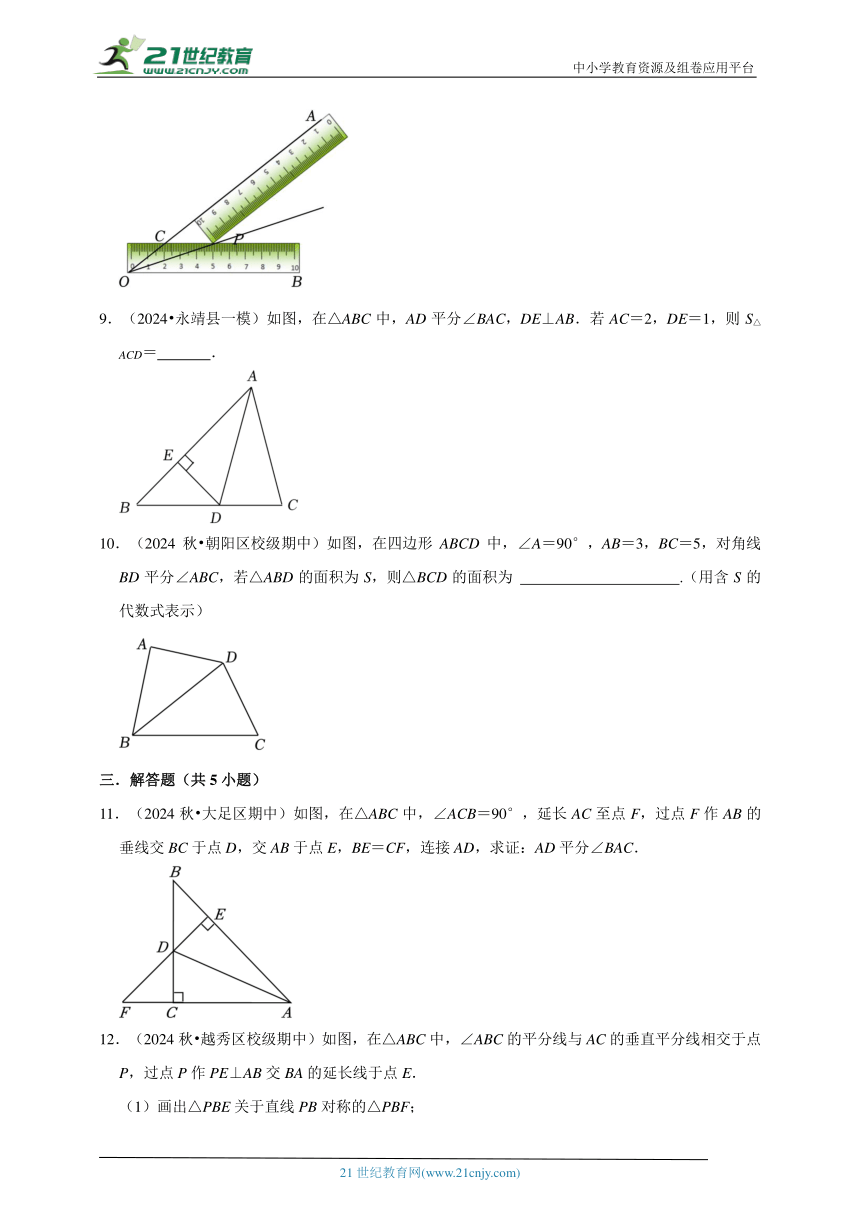
8.(2024 吉州区模拟)小明将两把完全相同的长方形直尺如图放置在∠AOB上,两把直尺的接触点为P,边OA与其中一把直尺边缘的交点为C,点C、P在这把直尺上的刻度读数分别是2、5,则OC的长度是 .
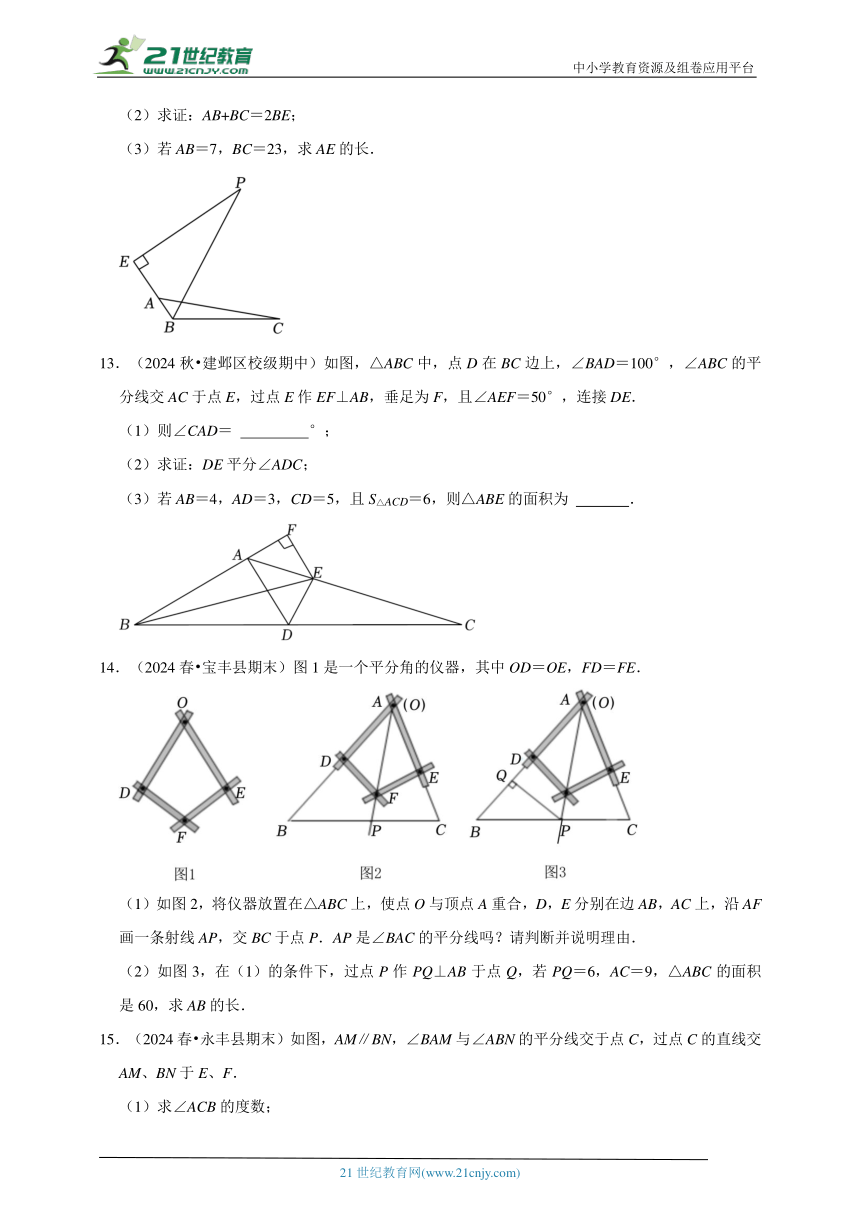
9.(2024 永靖县一模)如图,在△ABC中,AD平分∠BAC,DE⊥AB.若AC=2,DE=1,则S△ACD= .
10.(2024秋 朝阳区校级期中)如图,在四边形ABCD中,∠A=90°,AB=3,BC=5,对角线BD平分∠ABC,若△ABD的面积为S,则△BCD的面积为 .(用含S的代数式表示)
三.解答题(共5小题)
11.(2024秋 大足区期中)如图,在△ABC中,∠ACB=90°,延长AC至点F,过点F作AB的垂线交BC于点D,交AB于点E,BE=CF,连接AD,求证:AD平分∠BAC.
12.(2024秋 越秀区校级期中)如图,在△ABC中,∠ABC的平分线与AC的垂直平分线相交于点P,过点P作PE⊥AB交BA的延长线于点E.
(1)画出△PBE关于直线PB对称的△PBF;
(2)求证:AB+BC=2BE;
(3)若AB=7,BC=23,求AE的长.
13.(2024秋 建邺区校级期中)如图,△ABC中,点D在BC边上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)则∠CAD= °;
(2)求证:DE平分∠ADC;
(3)若AB=4,AD=3,CD=5,且S△ACD=6,则△ABE的面积为 .
14.(2024春 宝丰县期末)图1是一个平分角的仪器,其中OD=OE,FD=FE.
(1)如图2,将仪器放置在△ABC上,使点O与顶点A重合,D,E分别在边AB,AC上,沿AF画一条射线AP,交BC于点P.AP是∠BAC的平分线吗?请判断并说明理由.
(2)如图3,在(1)的条件下,过点P作PQ⊥AB于点Q,若PQ=6,AC=9,△ABC的面积是60,求AB的长.
15.(2024春 永丰县期末)如图,AM∥BN,∠BAM与∠ABN的平分线交于点C,过点C的直线交AM、BN于E、F.
(1)求∠ACB的度数;
(2)证明:CE=CF;
(3)若两平行线间的距离为4.8,线段AB长度为5,求AC BC的值.
预习衔接.夯实基础 角平分线
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 广州期中)如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于B,DF⊥AC于F,△ABC的面积是30,AB=13,AC=7,则DE的长( )
A.3 B.4 C.5 D.6
【考点】角平分线的性质.
【专题】三角形;推理能力.
【答案】A
【分析】根据角平分线的性质得到DE=DF,再根据三角形面积公式计算即可.
【解答】解:∵AD为∠BAC的平分线,DE⊥AB于B,DF⊥AC于F,
∴DE=DF,
∵△ABC的面积是30,AB=13,AC=7,
∴AB DEAC DF=30,即13 DE7 DE=30,
解得:DE=3,
故选:A.
【点评】本题考查的是角平分线的性质,角的平分线上的点到角的两边的距离相等.
2.(2024秋 惠阳区期中)如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,S△ABC=8,DE=2,AB=5,则AC长是( )
A.6 B.5 C.4 D.3
【考点】角平分线的性质.
【答案】D
【分析】根据角平分线性质求出DF,根据三角形面积公式求出△ABD的面积,求出△ADC面积,即可求出答案.
【解答】解:
过D作DF⊥AC于F,
∵AD是△ABC的角平分线,DE⊥AB,
∴DE=DF=2,
∵S△ADBAB×DE5×2=5,
∵△ABC的面积为8,
∴△ADC的面积为8﹣5=3,
∴AC×DF=3,
∴AC×2=3,
∴AC=3,
故选:D.
【点评】本题考查了角平分线性质,三角形的面积的应用,解此题的关键是求出DF长和三角形ADC的面积.
3.(2024秋 鹤山市期中)如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=30,BD:CD=3:2,则点D到AB的距离为( )
A.18 B.12 C.15 D.16
【考点】角平分线的性质.
【专题】等腰三角形与直角三角形;几何直观;推理能力.
【答案】B
【分析】作DE⊥AB于E,根据角平分线的性质得到CD=DE,根据题意求出CD的长即可.
【解答】解:作DE⊥AB于E,
∵BD:CD=3:2,BC=30,
∴CD=12,
∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴CD=DE=12,
故选:B.
【点评】本题主要考查角平分线的性质,由已知能够注意到D到AB的距离等于CD长是解决问题的关键.
4.(2024秋 越秀区校级期中)如图,一把直尺压住射线OB,另一把完全一样的直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的平分线.”他这样做的依据是( )
A.角平分线上的点到这个角两边的距离相等
B.角的内部到角的两边距离相等的点在角的平分线上
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
【考点】角平分线的性质;线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】B
【分析】根据角的内部到角的两边的距离相等的点在这个角的平分线上,可得OP平分∠AOB.
【解答】解:如图所示:过点P作PF⊥BO,PE⊥AO,
∵两把完全相同的长方形直尺的宽度相等,
∴PF=PE,
∴OP平分∠AOB,
所以B选项正确,符合题意,
故选:B.
【点评】此题主要考查了角平分线的性质,线段垂直平分线的性质,关键是掌握角的内部到角的两边的距离相等的点在这个角的平分线上.
5.(2024秋 秦淮区期中)如图,△ABC的边AB=10,BC=12,O是△ABC三条角平分线的交点,若△ABO的面积为15,则△BCO的面积为( )
A.11 B.17 C.18 D.20
【考点】角平分线的性质.
【专题】三角形;运算能力.
【答案】C
【分析】由角平分线的性质可得,点O到AB,BC,AC的距离相等,则△AOB、△BOC、△AOC面积的比实际为AB,BC,AC三边的比.
【解答】解:∵点O是三条角平分线的交点,
∴点O到BC,AB的距离相等,
∴△BOC的面积:△AOB面积=BC:AB=12:10=6:5.
∵△ABO的面积为15,
∴△BCO的面积为18.
故选:C.
【点评】此题主要考查角平分线的性质,解题的关键是理解角的平分线上的点到角的两边的距离相等.
二.填空题(共5小题)
6.(2024秋 翁源县期中)如图,射线OE是∠AOB的平分线,C是射线OE上一点,CF⊥OA于点F.若D是射线OB上一点,且OD=CF=6,则△ODC的面积是 18 .
【考点】角平分线的性质.
【专题】线段、角、相交线与平行线;三角形;推理能力.
【答案】18.
【分析】过C作CG⊥OB与G,由角平分线的性质推出CG=CF=6,由三角形面积公式得到△ODC的面积OD CG=18.
【解答】解:过C作CG⊥OB与G,
∵射线OE是∠AOB的平分线,CF⊥OA,
∴CG=CF=6,
∵OD=6,
∴△ODC的面积OD CG6×6=18.
故答案为:18.
【点评】本题考查角平分线的性质,三角形的面积,关键是由角平分线的性质推出CG=CF.
7.(2024秋 新吴区期中)如图,AD是△ABC的角平分线,DE⊥AB于点E,△ADC的面积=9,DE=2,则AC的长是 9 .
【考点】角平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】9.
【分析】根据题意得到DF=DE=2,再根据三角形面积公式即可求解.
【解答】解:过点D作DF⊥AC,交AC于点F,如图:
∵DF⊥AC,DE⊥AB,AD是△ABC的角平分线,DE=2,
∴DE=DF=2,
∵△ADC的面积AC DF=9,
∴AC=9,
故答案为:9.
【点评】本题考查了角平分线的性质,三角形面积公式,掌握角平分线的性质是解题的关键.
8.(2024 吉州区模拟)小明将两把完全相同的长方形直尺如图放置在∠AOB上,两把直尺的接触点为P,边OA与其中一把直尺边缘的交点为C,点C、P在这把直尺上的刻度读数分别是2、5,则OC的长度是 3cm .
【考点】角平分线的性质;平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】见试题解答内容
【分析】过P作PN⊥OB于N,由角平分线性质定理的逆定理推出PO平分∠AOB,得到∠COP=∠NOP,由平行线的性质推出∠CPO=∠NOP,得到∠COP=∠CPO,因此OC=PC,由PC=5﹣2=3(cm),即可得到OC的长度是3cm.
【解答】解:过P作PN⊥OB于N,
由题意得:PM=PN,
∵PM⊥OA,
∴PO平分∠AOB,
∴∠COP=∠NOP,
∵PC∥OB,
∴∠CPO=∠NOP,
∴∠COP=∠CPO,
∴OC=PC,
∵C、P在这把直尺上的刻度读数分别是2、5,
∴PC=5﹣2=3(cm),
∴OC的长度是3cm.
故答案为:3cm.
【点评】本题考查角平分线性质定理的逆定理,平行线的性质,关键是角平分线性质定理的逆定理证明PO平分∠AOB.
9.(2024 永靖县一模)如图,在△ABC中,AD平分∠BAC,DE⊥AB.若AC=2,DE=1,则S△ACD= 1 .
【考点】角平分线的性质.
【专题】三角形;运算能力.
【答案】见试题解答内容
【分析】过点D作DF⊥AC,垂足为F,根据角平分线的性质可得DE=DF=1,然后利用三角形的面积进行计算即可解答.
【解答】解:过点D作DF⊥AC,垂足为F,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF=1,
∵AC=2,
∴S△ACDAC DF
2×1
=1,
故答案为:1.
【点评】本题考查了角平分线的性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
10.(2024秋 朝阳区校级期中)如图,在四边形ABCD中,∠A=90°,AB=3,BC=5,对角线BD平分∠ABC,若△ABD的面积为S,则△BCD的面积为 .(用含S的代数式表示)
【考点】角平分线的性质;列代数式.
【专题】三角形;运算能力.
【答案】.
【分析】过点D作DE⊥BC,交BC于点E,利用角平分线的性质,得到DA=DE,利用S△BCDBC DE进行计算即可.
【解答】解:过点D作DE⊥BC,交BC于点E,
∵S△ABD AB AD=S,
∴AD,
∵∠A=90°,
∴DA⊥AB,
∵BD平分∠ABC,
∴DA=DE,
∴S△BCD BC DE5.
故答案为:.
【点评】本题考查角平分线的性质.熟练掌握角平分线上的点到角两边的距离相等,是解题的关键.
三.解答题(共5小题)
11.(2024秋 大足区期中)如图,在△ABC中,∠ACB=90°,延长AC至点F,过点F作AB的垂线交BC于点D,交AB于点E,BE=CF,连接AD,求证:AD平分∠BAC.
【考点】角平分线的性质;全等三角形的判定与性质.
【专题】三角形;图形的全等;几何直观;推理能力.
【答案】证明见解答过程.
【分析】先证明△DEB和△DCF全等得DE=DC,再根据角平分线的性质即可得出结论.
【解答】证明:∵FE⊥AB,∠ACB=90°,
∴∠DEB=∠DCF=90°,
在△DEB和△DCF中,
,
∴△DEB≌△DCF(AAS),
∴DE=DC,
∴点D在∠BAC的平分线上,
∴AD平分∠BAC.
【点评】此题主要考查了角平分线的性质,全等三角形的判定与性质,理解角平分线的性质,熟练掌握全等三角形的判定与性质是解决问题的关键.
12.(2024秋 越秀区校级期中)如图,在△ABC中,∠ABC的平分线与AC的垂直平分线相交于点P,过点P作PE⊥AB交BA的延长线于点E.
(1)画出△PBE关于直线PB对称的△PBF;
(2)求证:AB+BC=2BE;
(3)若AB=7,BC=23,求AE的长.
【考点】角平分线的性质;线段垂直平分线的性质;全等三角形的判定与性质.
【专题】线段、角、相交线与平行线;图形的全等;推理能力.
【答案】(1)见解析;
(2)见解析;
(3)8.
【分析】(1)由PB是∠ABC的平分线,且PE⊥AB,只需过点P作PF⊥BC于点F即可;
(2)连接PA,PC,证明Rt△PAE≌Rt△PHF(HL),得到CF=AE,进而得到AB+BC=AB+BF+CF=AB+BF+AE,结合BE=BF,即可得出结论;
(2)由(2)中结论即可求出BE=15,根据AE=BE﹣AB即可求解.
【解答】(1)解:如图所示,点P作PF⊥BC于点F,PF为所求,
∵PB是∠ABC的平分线,且PE⊥AB,PF⊥BC于点F,
∴PE=PF,∠PBE=∠PBF,
∵PB=PB,
∴Rt△PBE≌Rt△PBF(HL),
∴△PBE与△PBF关于直线PB对称;
(2)证明:连接PA,PC,
∵AC的垂直平分线过点P,
∴PA=PC,
∵∠PEB=∠PFC=90°,PE=PF,
∴Rt△PAE≌Rt△PCF(HL),
∴AE=CF,
∴AB+BC=AB+BF+CF=AB+BF+AE,
∵BE=BF,
∴AB+BC=AB+BE+AE=2BE;
(3)解:由(2)知AB+BC=2BE,
∵AB=7,BC=23,
∴AB+BC=2BE=30,
∴BE=15,
∴AE=BE﹣AB=8.
【点评】本题考查角平分线的性质,全等三角形的判定与性质,垂直平分线的性质,关键是全等三角形判定定理的应用.
13.(2024秋 建邺区校级期中)如图,△ABC中,点D在BC边上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)则∠CAD= 40 °;
(2)求证:DE平分∠ADC;
(3)若AB=4,AD=3,CD=5,且S△ACD=6,则△ABE的面积为 3 .
【考点】角平分线的性质;角平分线的定义;三角形的面积.
【专题】线段、角、相交线与平行线;三角形;运算能力.
【答案】(1)40;
(2)证明见解析;
(3)3.
【分析】(1)由直角三角形的性质求出∠EAF=90°﹣50°=40°,由平角定义得到∠CAD=40°;
(2)过E作EM⊥BC于M,EN⊥AD于N,由角平分线的性质推出EF=EN,EM=FE,得到EN=EM,即可证明DE平分∠ADC;
(3)由三角形面积公式得到(AD+CD)×EM=6,即可求出EM的出,即可求出△ABE的面积.
【解答】(1)解∵EF⊥AB,∠AEF=50°,
∴∠EAF=90°﹣50°=40°,
∵∠BAD=100°,
∴∠CAD=180°﹣100°﹣40°=40°;
故答案为:40;
(2)证明:过E作EM⊥BC于M,EN⊥AD于N,
∵∠EAF=∠CAD=40°,
∴AC平分∠DAF,
∵EN⊥AD,EF⊥AF,
∴EF=EN,
同理:EM=FE,
∴EN=EM,
∵EM⊥BC,EN⊥AD,
∴DE平分∠ADC;
(3)解:∵△ADE的面积+△CDE的面积=△ACD的面积,
∴AD ENCD EM=6,
∴(AD+CD)×EM=6,
∵AD=3,CD=5,
∴EM,
∴EF,
∴△ABE的面积AB EF43.
故答案为:3.
【点评】本题考查了角平分线的性质和定义,三角形的面积,熟练掌握角平分线上的点到角的两边的距离相等是解题关键.
14.(2024春 宝丰县期末)图1是一个平分角的仪器,其中OD=OE,FD=FE.
(1)如图2,将仪器放置在△ABC上,使点O与顶点A重合,D,E分别在边AB,AC上,沿AF画一条射线AP,交BC于点P.AP是∠BAC的平分线吗?请判断并说明理由.
(2)如图3,在(1)的条件下,过点P作PQ⊥AB于点Q,若PQ=6,AC=9,△ABC的面积是60,求AB的长.
【考点】角平分线的性质.
【专题】图形的全等;推理能力.
【答案】见试题解答内容
【分析】(1)是;理由:由(2)SSS判定△ADF≌△AEF,然后由该全等三角形的对应角相等证得结论;
(2)如图,过点P作PG⊥AC于点G.由三角形的面积公式作答即可.
【解答】解:(1)AP是∠BAC的平分线,理由如下:
在△ADF和△AEF中,
,
∴△ADF≌△AEF(SSS).
∴∠DAF=∠EAF,
∴AP平分∠BAC.
(2)如图,过点P作PG⊥AC于点G.
∵AP平分∠BAC,PQ⊥AB,
∴PG=PQ=6.
∵S△ABC=S△ABP+S△APCAB PQAC PG,
∴AB×69×6=60.
∴AB=11.
【点评】本题主要考查了全等三角形的判定与性质,三角形的面积公式以及角平分线的定义.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.
15.(2024春 永丰县期末)如图,AM∥BN,∠BAM与∠ABN的平分线交于点C,过点C的直线交AM、BN于E、F.
(1)求∠ACB的度数;
(2)证明:CE=CF;
(3)若两平行线间的距离为4.8,线段AB长度为5,求AC BC的值.
【考点】角平分线的性质;平行线之间的距离;全等三角形的判定与性质.
【专题】线段、角、相交线与平行线;三角形;图形的全等;几何直观;运算能力;推理能力.
【答案】(1)90°;
(2)答案见解答过程;
(3)12.
【分析】(1)过点C作CT∥AM,则AM∥BN∥CT,进而得∠1=∠CAM,∠2=∠CBN,∠BAM+∠ABN=180°,由此得∠ACB=∠CAM+∠CBN,再根据角平分线定义得∠CAM+∠CBN(∠BAM+∠ABN)=90°,据此可得∠ACB的度数;
(2)过点C作CP⊥AM于P,PC的延长线交BN于H,过点C作CK⊥AB于K,证明CH⊥BN,则∠CPE=∠CHF=90°,根据角平分线性质得CP=CK,CK=CH,则CP=CH=CK,由此可判定△CPE和△CHF全等,然后根据全等三角形的性质可得出结论;
(3)根据平行线间距离的定义得PH=4.8,由(2)可知CP=CH=CKPH=2.4,由(1)可知∠ACB=90°,然后根据三角形的面积公式可得出AC BC的值.
【解答】(1)解:过点C作CT∥AM,如图1所示:
∵AM∥BN,
∴AM∥BN∥CT,
∴∠1=∠CAM,∠2=∠CBN,∠BAM+∠ABN=180°,
∴∠1+∠2=∠CAM+∠CBN,
即∠ACB=∠CAM+∠CBN,
∵∠BAM与∠ABN的平分线交于点C,
∴∠CAM∠BAM,∠CBN∠ABN,
∴∠CAM+∠CBN(∠BAM+∠ABN)=90°,
∴∠ACB=90°;
(2)证明:过点C作CP⊥AM于P,PC的延长线交BN于H,过点C作CK⊥AB于K,如图所示:
∵AM∥BN,
∴CH⊥BN,
∴∠CPE=∠CHF=90°,
∵∠BAM与∠ABN的平分线交于点C,
∴CP=CK,CK=CH,
∴CP=CH=CK,
在△CPE和△CHF中,
,
∴△CPE≌△CHF(ASA),
∴CE=CF;
(3)解:∵平行线AM,BN之间的距离为4.8,
∴PH=4.8,
由(2)可知:CP=CH=CKPH=2.4,
由(1)可知:∠ACB=90°,
∴S△ABCAC BCAB CK,
∵AB=5,
∴AC BC=AB CK=5×2.4=12.
【点评】此题主要考查了角平分线的性质,平行线之间的距离,全等三角形的判定和性质,理解角平分线的性质,平行线之间的距离,熟练掌握全等三角形的判定和性质是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.夯实基础 角平分线
一.选择题(共5小题)
1.(2024秋 广州期中)如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于B,DF⊥AC于F,△ABC的面积是30,AB=13,AC=7,则DE的长( )
A.3 B.4 C.5 D.6
2.(2024秋 惠阳区期中)如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,S△ABC=8,DE=2,AB=5,则AC长是( )
A.6 B.5 C.4 D.3
3.(2024秋 鹤山市期中)如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=30,BD:CD=3:2,则点D到AB的距离为( )
A.18 B.12 C.15 D.16
4.(2024秋 越秀区校级期中)如图,一把直尺压住射线OB,另一把完全一样的直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的平分线.”他这样做的依据是( )
A.角平分线上的点到这个角两边的距离相等
B.角的内部到角的两边距离相等的点在角的平分线上
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
5.(2024秋 秦淮区期中)如图,△ABC的边AB=10,BC=12,O是△ABC三条角平分线的交点,若△ABO的面积为15,则△BCO的面积为( )
A.11 B.17 C.18 D.20
二.填空题(共5小题)
6.(2024秋 翁源县期中)如图,射线OE是∠AOB的平分线,C是射线OE上一点,CF⊥OA于点F.若D是射线OB上一点,且OD=CF=6,则△ODC的面积是 .
7.(2024秋 新吴区期中)如图,AD是△ABC的角平分线,DE⊥AB于点E,△ADC的面积=9,DE=2,则AC的长是 .
8.(2024 吉州区模拟)小明将两把完全相同的长方形直尺如图放置在∠AOB上,两把直尺的接触点为P,边OA与其中一把直尺边缘的交点为C,点C、P在这把直尺上的刻度读数分别是2、5,则OC的长度是 .
9.(2024 永靖县一模)如图,在△ABC中,AD平分∠BAC,DE⊥AB.若AC=2,DE=1,则S△ACD= .
10.(2024秋 朝阳区校级期中)如图,在四边形ABCD中,∠A=90°,AB=3,BC=5,对角线BD平分∠ABC,若△ABD的面积为S,则△BCD的面积为 .(用含S的代数式表示)
三.解答题(共5小题)
11.(2024秋 大足区期中)如图,在△ABC中,∠ACB=90°,延长AC至点F,过点F作AB的垂线交BC于点D,交AB于点E,BE=CF,连接AD,求证:AD平分∠BAC.
12.(2024秋 越秀区校级期中)如图,在△ABC中,∠ABC的平分线与AC的垂直平分线相交于点P,过点P作PE⊥AB交BA的延长线于点E.
(1)画出△PBE关于直线PB对称的△PBF;
(2)求证:AB+BC=2BE;
(3)若AB=7,BC=23,求AE的长.
13.(2024秋 建邺区校级期中)如图,△ABC中,点D在BC边上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)则∠CAD= °;
(2)求证:DE平分∠ADC;
(3)若AB=4,AD=3,CD=5,且S△ACD=6,则△ABE的面积为 .
14.(2024春 宝丰县期末)图1是一个平分角的仪器,其中OD=OE,FD=FE.
(1)如图2,将仪器放置在△ABC上,使点O与顶点A重合,D,E分别在边AB,AC上,沿AF画一条射线AP,交BC于点P.AP是∠BAC的平分线吗?请判断并说明理由.
(2)如图3,在(1)的条件下,过点P作PQ⊥AB于点Q,若PQ=6,AC=9,△ABC的面积是60,求AB的长.
15.(2024春 永丰县期末)如图,AM∥BN,∠BAM与∠ABN的平分线交于点C,过点C的直线交AM、BN于E、F.
(1)求∠ACB的度数;
(2)证明:CE=CF;
(3)若两平行线间的距离为4.8,线段AB长度为5,求AC BC的值.
预习衔接.夯实基础 角平分线
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 广州期中)如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于B,DF⊥AC于F,△ABC的面积是30,AB=13,AC=7,则DE的长( )
A.3 B.4 C.5 D.6
【考点】角平分线的性质.
【专题】三角形;推理能力.
【答案】A
【分析】根据角平分线的性质得到DE=DF,再根据三角形面积公式计算即可.
【解答】解:∵AD为∠BAC的平分线,DE⊥AB于B,DF⊥AC于F,
∴DE=DF,
∵△ABC的面积是30,AB=13,AC=7,
∴AB DEAC DF=30,即13 DE7 DE=30,
解得:DE=3,
故选:A.
【点评】本题考查的是角平分线的性质,角的平分线上的点到角的两边的距离相等.
2.(2024秋 惠阳区期中)如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,S△ABC=8,DE=2,AB=5,则AC长是( )
A.6 B.5 C.4 D.3
【考点】角平分线的性质.
【答案】D
【分析】根据角平分线性质求出DF,根据三角形面积公式求出△ABD的面积,求出△ADC面积,即可求出答案.
【解答】解:
过D作DF⊥AC于F,
∵AD是△ABC的角平分线,DE⊥AB,
∴DE=DF=2,
∵S△ADBAB×DE5×2=5,
∵△ABC的面积为8,
∴△ADC的面积为8﹣5=3,
∴AC×DF=3,
∴AC×2=3,
∴AC=3,
故选:D.
【点评】本题考查了角平分线性质,三角形的面积的应用,解此题的关键是求出DF长和三角形ADC的面积.
3.(2024秋 鹤山市期中)如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=30,BD:CD=3:2,则点D到AB的距离为( )
A.18 B.12 C.15 D.16
【考点】角平分线的性质.
【专题】等腰三角形与直角三角形;几何直观;推理能力.
【答案】B
【分析】作DE⊥AB于E,根据角平分线的性质得到CD=DE,根据题意求出CD的长即可.
【解答】解:作DE⊥AB于E,
∵BD:CD=3:2,BC=30,
∴CD=12,
∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴CD=DE=12,
故选:B.
【点评】本题主要考查角平分线的性质,由已知能够注意到D到AB的距离等于CD长是解决问题的关键.
4.(2024秋 越秀区校级期中)如图,一把直尺压住射线OB,另一把完全一样的直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的平分线.”他这样做的依据是( )
A.角平分线上的点到这个角两边的距离相等
B.角的内部到角的两边距离相等的点在角的平分线上
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
【考点】角平分线的性质;线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】B
【分析】根据角的内部到角的两边的距离相等的点在这个角的平分线上,可得OP平分∠AOB.
【解答】解:如图所示:过点P作PF⊥BO,PE⊥AO,
∵两把完全相同的长方形直尺的宽度相等,
∴PF=PE,
∴OP平分∠AOB,
所以B选项正确,符合题意,
故选:B.
【点评】此题主要考查了角平分线的性质,线段垂直平分线的性质,关键是掌握角的内部到角的两边的距离相等的点在这个角的平分线上.
5.(2024秋 秦淮区期中)如图,△ABC的边AB=10,BC=12,O是△ABC三条角平分线的交点,若△ABO的面积为15,则△BCO的面积为( )
A.11 B.17 C.18 D.20
【考点】角平分线的性质.
【专题】三角形;运算能力.
【答案】C
【分析】由角平分线的性质可得,点O到AB,BC,AC的距离相等,则△AOB、△BOC、△AOC面积的比实际为AB,BC,AC三边的比.
【解答】解:∵点O是三条角平分线的交点,
∴点O到BC,AB的距离相等,
∴△BOC的面积:△AOB面积=BC:AB=12:10=6:5.
∵△ABO的面积为15,
∴△BCO的面积为18.
故选:C.
【点评】此题主要考查角平分线的性质,解题的关键是理解角的平分线上的点到角的两边的距离相等.
二.填空题(共5小题)
6.(2024秋 翁源县期中)如图,射线OE是∠AOB的平分线,C是射线OE上一点,CF⊥OA于点F.若D是射线OB上一点,且OD=CF=6,则△ODC的面积是 18 .
【考点】角平分线的性质.
【专题】线段、角、相交线与平行线;三角形;推理能力.
【答案】18.
【分析】过C作CG⊥OB与G,由角平分线的性质推出CG=CF=6,由三角形面积公式得到△ODC的面积OD CG=18.
【解答】解:过C作CG⊥OB与G,
∵射线OE是∠AOB的平分线,CF⊥OA,
∴CG=CF=6,
∵OD=6,
∴△ODC的面积OD CG6×6=18.
故答案为:18.
【点评】本题考查角平分线的性质,三角形的面积,关键是由角平分线的性质推出CG=CF.
7.(2024秋 新吴区期中)如图,AD是△ABC的角平分线,DE⊥AB于点E,△ADC的面积=9,DE=2,则AC的长是 9 .
【考点】角平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】9.
【分析】根据题意得到DF=DE=2,再根据三角形面积公式即可求解.
【解答】解:过点D作DF⊥AC,交AC于点F,如图:
∵DF⊥AC,DE⊥AB,AD是△ABC的角平分线,DE=2,
∴DE=DF=2,
∵△ADC的面积AC DF=9,
∴AC=9,
故答案为:9.
【点评】本题考查了角平分线的性质,三角形面积公式,掌握角平分线的性质是解题的关键.
8.(2024 吉州区模拟)小明将两把完全相同的长方形直尺如图放置在∠AOB上,两把直尺的接触点为P,边OA与其中一把直尺边缘的交点为C,点C、P在这把直尺上的刻度读数分别是2、5,则OC的长度是 3cm .
【考点】角平分线的性质;平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】见试题解答内容
【分析】过P作PN⊥OB于N,由角平分线性质定理的逆定理推出PO平分∠AOB,得到∠COP=∠NOP,由平行线的性质推出∠CPO=∠NOP,得到∠COP=∠CPO,因此OC=PC,由PC=5﹣2=3(cm),即可得到OC的长度是3cm.
【解答】解:过P作PN⊥OB于N,
由题意得:PM=PN,
∵PM⊥OA,
∴PO平分∠AOB,
∴∠COP=∠NOP,
∵PC∥OB,
∴∠CPO=∠NOP,
∴∠COP=∠CPO,
∴OC=PC,
∵C、P在这把直尺上的刻度读数分别是2、5,
∴PC=5﹣2=3(cm),
∴OC的长度是3cm.
故答案为:3cm.
【点评】本题考查角平分线性质定理的逆定理,平行线的性质,关键是角平分线性质定理的逆定理证明PO平分∠AOB.
9.(2024 永靖县一模)如图,在△ABC中,AD平分∠BAC,DE⊥AB.若AC=2,DE=1,则S△ACD= 1 .
【考点】角平分线的性质.
【专题】三角形;运算能力.
【答案】见试题解答内容
【分析】过点D作DF⊥AC,垂足为F,根据角平分线的性质可得DE=DF=1,然后利用三角形的面积进行计算即可解答.
【解答】解:过点D作DF⊥AC,垂足为F,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF=1,
∵AC=2,
∴S△ACDAC DF
2×1
=1,
故答案为:1.
【点评】本题考查了角平分线的性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
10.(2024秋 朝阳区校级期中)如图,在四边形ABCD中,∠A=90°,AB=3,BC=5,对角线BD平分∠ABC,若△ABD的面积为S,则△BCD的面积为 .(用含S的代数式表示)
【考点】角平分线的性质;列代数式.
【专题】三角形;运算能力.
【答案】.
【分析】过点D作DE⊥BC,交BC于点E,利用角平分线的性质,得到DA=DE,利用S△BCDBC DE进行计算即可.
【解答】解:过点D作DE⊥BC,交BC于点E,
∵S△ABD AB AD=S,
∴AD,
∵∠A=90°,
∴DA⊥AB,
∵BD平分∠ABC,
∴DA=DE,
∴S△BCD BC DE5.
故答案为:.
【点评】本题考查角平分线的性质.熟练掌握角平分线上的点到角两边的距离相等,是解题的关键.
三.解答题(共5小题)
11.(2024秋 大足区期中)如图,在△ABC中,∠ACB=90°,延长AC至点F,过点F作AB的垂线交BC于点D,交AB于点E,BE=CF,连接AD,求证:AD平分∠BAC.
【考点】角平分线的性质;全等三角形的判定与性质.
【专题】三角形;图形的全等;几何直观;推理能力.
【答案】证明见解答过程.
【分析】先证明△DEB和△DCF全等得DE=DC,再根据角平分线的性质即可得出结论.
【解答】证明:∵FE⊥AB,∠ACB=90°,
∴∠DEB=∠DCF=90°,
在△DEB和△DCF中,
,
∴△DEB≌△DCF(AAS),
∴DE=DC,
∴点D在∠BAC的平分线上,
∴AD平分∠BAC.
【点评】此题主要考查了角平分线的性质,全等三角形的判定与性质,理解角平分线的性质,熟练掌握全等三角形的判定与性质是解决问题的关键.
12.(2024秋 越秀区校级期中)如图,在△ABC中,∠ABC的平分线与AC的垂直平分线相交于点P,过点P作PE⊥AB交BA的延长线于点E.
(1)画出△PBE关于直线PB对称的△PBF;
(2)求证:AB+BC=2BE;
(3)若AB=7,BC=23,求AE的长.
【考点】角平分线的性质;线段垂直平分线的性质;全等三角形的判定与性质.
【专题】线段、角、相交线与平行线;图形的全等;推理能力.
【答案】(1)见解析;
(2)见解析;
(3)8.
【分析】(1)由PB是∠ABC的平分线,且PE⊥AB,只需过点P作PF⊥BC于点F即可;
(2)连接PA,PC,证明Rt△PAE≌Rt△PHF(HL),得到CF=AE,进而得到AB+BC=AB+BF+CF=AB+BF+AE,结合BE=BF,即可得出结论;
(2)由(2)中结论即可求出BE=15,根据AE=BE﹣AB即可求解.
【解答】(1)解:如图所示,点P作PF⊥BC于点F,PF为所求,
∵PB是∠ABC的平分线,且PE⊥AB,PF⊥BC于点F,
∴PE=PF,∠PBE=∠PBF,
∵PB=PB,
∴Rt△PBE≌Rt△PBF(HL),
∴△PBE与△PBF关于直线PB对称;
(2)证明:连接PA,PC,
∵AC的垂直平分线过点P,
∴PA=PC,
∵∠PEB=∠PFC=90°,PE=PF,
∴Rt△PAE≌Rt△PCF(HL),
∴AE=CF,
∴AB+BC=AB+BF+CF=AB+BF+AE,
∵BE=BF,
∴AB+BC=AB+BE+AE=2BE;
(3)解:由(2)知AB+BC=2BE,
∵AB=7,BC=23,
∴AB+BC=2BE=30,
∴BE=15,
∴AE=BE﹣AB=8.
【点评】本题考查角平分线的性质,全等三角形的判定与性质,垂直平分线的性质,关键是全等三角形判定定理的应用.
13.(2024秋 建邺区校级期中)如图,△ABC中,点D在BC边上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)则∠CAD= 40 °;
(2)求证:DE平分∠ADC;
(3)若AB=4,AD=3,CD=5,且S△ACD=6,则△ABE的面积为 3 .
【考点】角平分线的性质;角平分线的定义;三角形的面积.
【专题】线段、角、相交线与平行线;三角形;运算能力.
【答案】(1)40;
(2)证明见解析;
(3)3.
【分析】(1)由直角三角形的性质求出∠EAF=90°﹣50°=40°,由平角定义得到∠CAD=40°;
(2)过E作EM⊥BC于M,EN⊥AD于N,由角平分线的性质推出EF=EN,EM=FE,得到EN=EM,即可证明DE平分∠ADC;
(3)由三角形面积公式得到(AD+CD)×EM=6,即可求出EM的出,即可求出△ABE的面积.
【解答】(1)解∵EF⊥AB,∠AEF=50°,
∴∠EAF=90°﹣50°=40°,
∵∠BAD=100°,
∴∠CAD=180°﹣100°﹣40°=40°;
故答案为:40;
(2)证明:过E作EM⊥BC于M,EN⊥AD于N,
∵∠EAF=∠CAD=40°,
∴AC平分∠DAF,
∵EN⊥AD,EF⊥AF,
∴EF=EN,
同理:EM=FE,
∴EN=EM,
∵EM⊥BC,EN⊥AD,
∴DE平分∠ADC;
(3)解:∵△ADE的面积+△CDE的面积=△ACD的面积,
∴AD ENCD EM=6,
∴(AD+CD)×EM=6,
∵AD=3,CD=5,
∴EM,
∴EF,
∴△ABE的面积AB EF43.
故答案为:3.
【点评】本题考查了角平分线的性质和定义,三角形的面积,熟练掌握角平分线上的点到角的两边的距离相等是解题关键.
14.(2024春 宝丰县期末)图1是一个平分角的仪器,其中OD=OE,FD=FE.
(1)如图2,将仪器放置在△ABC上,使点O与顶点A重合,D,E分别在边AB,AC上,沿AF画一条射线AP,交BC于点P.AP是∠BAC的平分线吗?请判断并说明理由.
(2)如图3,在(1)的条件下,过点P作PQ⊥AB于点Q,若PQ=6,AC=9,△ABC的面积是60,求AB的长.
【考点】角平分线的性质.
【专题】图形的全等;推理能力.
【答案】见试题解答内容
【分析】(1)是;理由:由(2)SSS判定△ADF≌△AEF,然后由该全等三角形的对应角相等证得结论;
(2)如图,过点P作PG⊥AC于点G.由三角形的面积公式作答即可.
【解答】解:(1)AP是∠BAC的平分线,理由如下:
在△ADF和△AEF中,
,
∴△ADF≌△AEF(SSS).
∴∠DAF=∠EAF,
∴AP平分∠BAC.
(2)如图,过点P作PG⊥AC于点G.
∵AP平分∠BAC,PQ⊥AB,
∴PG=PQ=6.
∵S△ABC=S△ABP+S△APCAB PQAC PG,
∴AB×69×6=60.
∴AB=11.
【点评】本题主要考查了全等三角形的判定与性质,三角形的面积公式以及角平分线的定义.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.
15.(2024春 永丰县期末)如图,AM∥BN,∠BAM与∠ABN的平分线交于点C,过点C的直线交AM、BN于E、F.
(1)求∠ACB的度数;
(2)证明:CE=CF;
(3)若两平行线间的距离为4.8,线段AB长度为5,求AC BC的值.
【考点】角平分线的性质;平行线之间的距离;全等三角形的判定与性质.
【专题】线段、角、相交线与平行线;三角形;图形的全等;几何直观;运算能力;推理能力.
【答案】(1)90°;
(2)答案见解答过程;
(3)12.
【分析】(1)过点C作CT∥AM,则AM∥BN∥CT,进而得∠1=∠CAM,∠2=∠CBN,∠BAM+∠ABN=180°,由此得∠ACB=∠CAM+∠CBN,再根据角平分线定义得∠CAM+∠CBN(∠BAM+∠ABN)=90°,据此可得∠ACB的度数;
(2)过点C作CP⊥AM于P,PC的延长线交BN于H,过点C作CK⊥AB于K,证明CH⊥BN,则∠CPE=∠CHF=90°,根据角平分线性质得CP=CK,CK=CH,则CP=CH=CK,由此可判定△CPE和△CHF全等,然后根据全等三角形的性质可得出结论;
(3)根据平行线间距离的定义得PH=4.8,由(2)可知CP=CH=CKPH=2.4,由(1)可知∠ACB=90°,然后根据三角形的面积公式可得出AC BC的值.
【解答】(1)解:过点C作CT∥AM,如图1所示:
∵AM∥BN,
∴AM∥BN∥CT,
∴∠1=∠CAM,∠2=∠CBN,∠BAM+∠ABN=180°,
∴∠1+∠2=∠CAM+∠CBN,
即∠ACB=∠CAM+∠CBN,
∵∠BAM与∠ABN的平分线交于点C,
∴∠CAM∠BAM,∠CBN∠ABN,
∴∠CAM+∠CBN(∠BAM+∠ABN)=90°,
∴∠ACB=90°;
(2)证明:过点C作CP⊥AM于P,PC的延长线交BN于H,过点C作CK⊥AB于K,如图所示:
∵AM∥BN,
∴CH⊥BN,
∴∠CPE=∠CHF=90°,
∵∠BAM与∠ABN的平分线交于点C,
∴CP=CK,CK=CH,
∴CP=CH=CK,
在△CPE和△CHF中,
,
∴△CPE≌△CHF(ASA),
∴CE=CF;
(3)解:∵平行线AM,BN之间的距离为4.8,
∴PH=4.8,
由(2)可知:CP=CH=CKPH=2.4,
由(1)可知:∠ACB=90°,
∴S△ABCAC BCAB CK,
∵AB=5,
∴AC BC=AB CK=5×2.4=12.
【点评】此题主要考查了角平分线的性质,平行线之间的距离,全等三角形的判定和性质,理解角平分线的性质,平行线之间的距离,熟练掌握全等三角形的判定和性质是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
