13.1勾股定理及其逆定理(预习衔接.夯实基础.含解析)-2025-2026学年八年级上册数学华东师大版(2024)
文档属性
| 名称 | 13.1勾股定理及其逆定理(预习衔接.夯实基础.含解析)-2025-2026学年八年级上册数学华东师大版(2024) |
|
|
| 格式 | docx | ||
| 文件大小 | 162.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 21:24:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
预习衔接.夯实基础 勾股定理及其逆定理
一.选择题(共5小题)
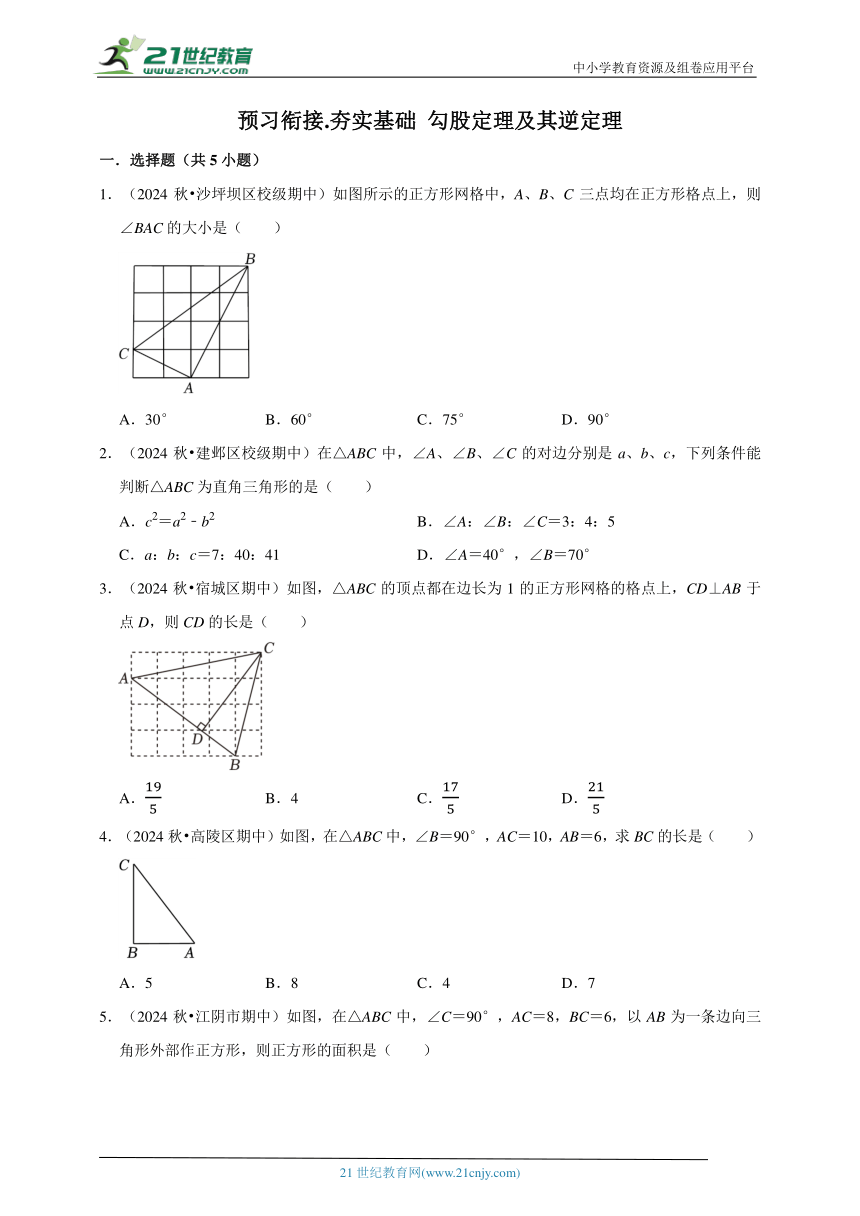
1.(2024秋 沙坪坝区校级期中)如图所示的正方形网格中,A、B、C三点均在正方形格点上,则∠BAC的大小是( )
A.30° B.60° C.75° D.90°
2.(2024秋 建邺区校级期中)在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列条件能判断△ABC为直角三角形的是( )
A.c2=a2﹣b2 B.∠A:∠B:∠C=3:4:5
C.a:b:c=7:40:41 D.∠A=40°,∠B=70°
3.(2024秋 宿城区期中)如图,△ABC的顶点都在边长为1的正方形网格的格点上,CD⊥AB于点D,则CD的长是( )
A. B.4 C. D.
4.(2024秋 高陵区期中)如图,在△ABC中,∠B=90°,AC=10,AB=6,求BC的长是( )
A.5 B.8 C.4 D.7
5.(2024秋 江阴市期中)如图,在△ABC中,∠C=90°,AC=8,BC=6,以AB为一条边向三角形外部作正方形,则正方形的面积是( )
A.100 B.80 C.48 D.24
二.解答题(共5小题)
6.(2024秋 深圳期中)如图,已知等腰△ABC的底边BC=13,D是腰AB上一点,且CD=5,BD=12.
(1)BD与AC垂直吗?请说明理由.
(2)求AD的长.
7.(2024秋 九原区期中)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,AB=13,BC=5,求AC、CD的长.
8.(2024秋 惠山区期中)水利是农业的命脉,开远民间历来重视兴修水利,坝区明代即已筑堰修渠,开通东沟、西沟,引泸江、南洞水灌溉农田,经历代不断修拓完善,成为城郊灌溉干渠.这些沟渠凝聚了一代又一代开远人的智慧和心血,历经岁月磨砺、时光雕琢,成为最美的风景,在开远东沟的一侧有一个花卉基地,基地到东沟原有两个取水点A,B,其中AB=AC,为方便花卉基地取水,决定在东沟新建一个取水点D(A、D、B在同一条直线上),并新修一条路CD,测得BC=39m,CD=36m,BD=15m.
(1)求证:CD⊥AB;
(2)求新路CD比原来的路AC少多少米.
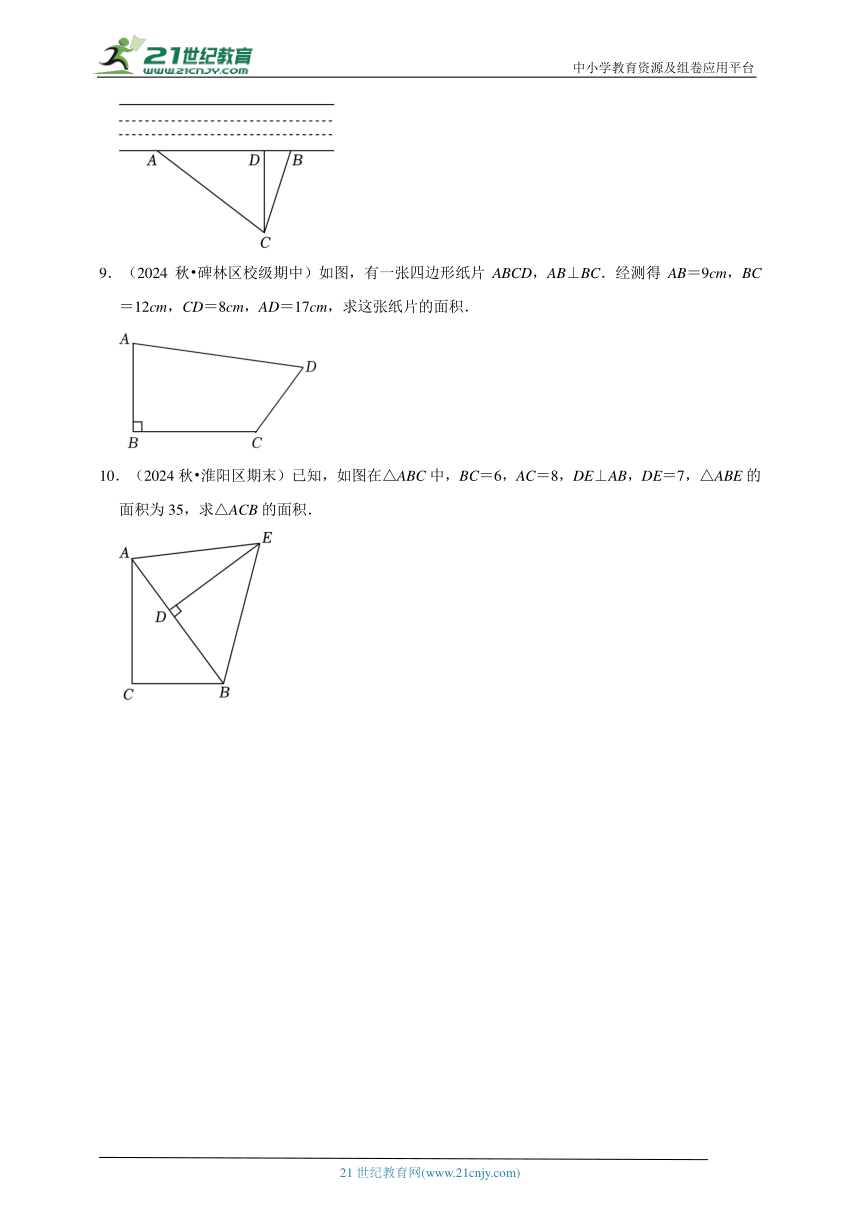
9.(2024秋 碑林区校级期中)如图,有一张四边形纸片ABCD,AB⊥BC.经测得AB=9cm,BC=12cm,CD=8cm,AD=17cm,求这张纸片的面积.
10.(2024秋 淮阳区期末)已知,如图在△ABC中,BC=6,AC=8,DE⊥AB,DE=7,△ABE的面积为35,求△ACB的面积.
预习衔接.夯实基础 勾股定理及其逆定理
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 沙坪坝区校级期中)如图所示的正方形网格中,A、B、C三点均在正方形格点上,则∠BAC的大小是( )
A.30° B.60° C.75° D.90°
【考点】勾股定理的逆定理;勾股定理.
【专题】等腰三角形与直角三角形;运算能力.
【答案】D
【分析】利用勾股定理的逆定理证明△ABC是直角三角形,从而可得∠BAC=90°,即可解答.
【解答】解:由题意得:AB2=22+42=20,AC2=12+22=5,BC2=32+42=25,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
∴∠BAC=90°,
故选:D.
【点评】本题考查了勾股定理,勾股定理的逆定理,熟练掌握勾股定理以及勾股定理的逆定理是解题的关键.
2.(2024秋 建邺区校级期中)在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列条件能判断△ABC为直角三角形的是( )
A.c2=a2﹣b2 B.∠A:∠B:∠C=3:4:5
C.a:b:c=7:40:41 D.∠A=40°,∠B=70°
【考点】勾股定理的逆定理;三角形内角和定理.
【专题】等腰三角形与直角三角形;推理能力.
【答案】A
【分析】根据勾股定理和三角形内角和定理对各选项进行逐一判断即可.
【解答】解:A、∵c2=a2﹣b2,
∴c2+b2=a2,
∴△ABC是直角三角形,符合题意;
B、∵∠A:∠B:∠C=3:4:5,∠A+∠B+∠C=180°,
∴最大角∠C180°=75°,
∴△ABC不是直角三角形,不符合题意;
C、∵72+402≠412,
∴△ABC不是直角三角形,不符合题意;
D、∵∠A=40°,∠B=70°,
∴∠C=180°﹣40°﹣70°=70°,
∴△ABC不是直角三角形,不符合题意.
故选:A.
【点评】本题考查的是勾股定理的逆定理及三角形内角和定理,熟知以上知识是解题的关键.
3.(2024秋 宿城区期中)如图,△ABC的顶点都在边长为1的正方形网格的格点上,CD⊥AB于点D,则CD的长是( )
A. B.4 C. D.
【考点】勾股定理.
【专题】等腰三角形与直角三角形;运算能力;推理能力.
【答案】A
【分析】通过勾股定理求出AB的长度,利用面积割补法求出△ABC的面积,再利用等面积求出CD即可.
【解答】解:如图,由勾股定理得 AB5,
∵S△ABC=S长方形CGHK﹣S△CKA﹣S△ABH﹣S△CBG=206﹣2,
又∵S△ABCAB CD,
∴5×CD,
∴CD,
故选:A.
【点评】本题考查了勾股定理,三角形的面积,熟练掌握勾股定理是解题的关键.
4.(2024秋 高陵区期中)如图,在△ABC中,∠B=90°,AC=10,AB=6,求BC的长是( )
A.5 B.8 C.4 D.7
【考点】勾股定理.
【专题】等腰三角形与直角三角形;几何直观;推理能力.
【答案】B
【分析】根据勾股定理得到AB2+BC2=AC2,代入计算即可得BC的值.
【解答】解:在△ABC中,∠B=90°,AC=10,AB=6,
由勾股定理得:AB2+BC2=AC2,
∴6+BC2=102,
∴BC=8(负值舍去),
故选:B.
【点评】本题考查了勾股定理,解答本题的关键是熟练运用数形结合的思想解决问题.
5.(2024秋 江阴市期中)如图,在△ABC中,∠C=90°,AC=8,BC=6,以AB为一条边向三角形外部作正方形,则正方形的面积是( )
A.100 B.80 C.48 D.24
【考点】勾股定理.
【专题】等腰三角形与直角三角形;运算能力;推理能力.
【答案】A
【分析】根据勾股定理和正方形的面积公式即可得到结论.
【解答】解:在△ABC中,∠C=90°,AC=8,BC=6,
∴AB2=AC2+BC2=82+62=100,
∴正方形的面积=AB2=100,
故选:A.
【点评】本题考查了勾股定理、正方形的面积计算等知识,熟练掌握勾股定理是解题的关键.
二.解答题(共5小题)
6.(2024秋 深圳期中)如图,已知等腰△ABC的底边BC=13,D是腰AB上一点,且CD=5,BD=12.
(1)BD与AC垂直吗?请说明理由.
(2)求AD的长.
【考点】勾股定理的逆定理;等腰三角形的性质;勾股定理.
【专题】等腰三角形与直角三角形;推理能力.
【答案】(1)垂直,理由见解析;
(2)11.9.
【分析】(1)由BC=13,CD=5,BD=12得出△BCD是直角三角形,故可得出BD⊥AC;
(2)设AD=x,则AC=AB=x+CD=x+5,再由勾股定理求出x的值即可.
【解答】解:(1)垂直,理由:
∵BC=13,CD=5,BD=12,132=52+122,
∴BC2=CD2+BD2,
∴△BDC为直角三角形且∠BDC=90°,
∴BD与AC垂直;
(2)由(1)知,BD⊥AC,
∵等腰△ABC的底边BC=13,D是腰AB上一点,且CD=5,BD=12,
∴设AD=x,则AC=AB=x+CD=x+5,
∴AD2+BD2=AB2,即x2+122=(x+5)2,
解得x=11.9,
∴AD=11.9.
【点评】此题考查等腰三角形的性质、勾股定理以及逆定理的应用,解题的关键是掌握以上知识.
7.(2024秋 九原区期中)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,AB=13,BC=5,求AC、CD的长.
【考点】勾股定理.
【专题】等腰三角形与直角三角形;推理能力.
【答案】.
【分析】在Rt△ABC中,勾股定理求得AC的长,进而等面积法求得CD,即可求解.
【解答】解:在Rt△ABC中,∠ACB=90°
12,
∵∠ACB=90°,CD⊥AB,
∴,
∴.
【点评】本题考查了勾股定理,熟练掌握勾股定理是解题的关键.
8.(2024秋 惠山区期中)水利是农业的命脉,开远民间历来重视兴修水利,坝区明代即已筑堰修渠,开通东沟、西沟,引泸江、南洞水灌溉农田,经历代不断修拓完善,成为城郊灌溉干渠.这些沟渠凝聚了一代又一代开远人的智慧和心血,历经岁月磨砺、时光雕琢,成为最美的风景,在开远东沟的一侧有一个花卉基地,基地到东沟原有两个取水点A,B,其中AB=AC,为方便花卉基地取水,决定在东沟新建一个取水点D(A、D、B在同一条直线上),并新修一条路CD,测得BC=39m,CD=36m,BD=15m.
(1)求证:CD⊥AB;
(2)求新路CD比原来的路AC少多少米.
【考点】勾股定理的逆定理;两点间的距离.
【专题】等腰三角形与直角三角形;推理能力.
【答案】(1)证明见解析;
(2)14.7米.
【分析】(1)根据勾股定理的逆定理解答即可;
(2)设AC=x m,则AD=(x﹣15)m,在直角△ACD中根据勾股定理求出x的值,进而可得出结论.
【解答】(1)证明:∵BC=39m,CD=36m,BD=15m,362+152=392,
∴CD2+BD2=CB2,
∴△CDB为直角三角形,
∴CD⊥AB;
(2)解:设AC=x m,则AD=(x﹣15)m,
∵CD⊥AB,∠ADC=90°,
∴CD2+AD2=AC2,即362+(x﹣15)2=x2,
解得x=50.7,
∴AC﹣CD=50.7﹣36=14.7(m),
答:新路CD比原来的路AC少14.7米.
【点评】此题考查了勾股定理的逆定理,两点间的距离,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解题的关键.
9.(2024秋 碑林区校级期中)如图,有一张四边形纸片ABCD,AB⊥BC.经测得AB=9cm,BC=12cm,CD=8cm,AD=17cm,求这张纸片的面积.
【考点】勾股定理的逆定理;勾股定理.
【专题】等腰三角形与直角三角形;推理能力.
【答案】114cm2.
【分析】根据勾股定理逆定理证得∠ACD=90°,由于四边形纸片ABCD的面积=S△ABC+S△ACD,根据三角形的面积公式即可求得结论.
【解答】解:如图,连接AC,
在Rt△ABC中,AB⊥BC,AB=9cm,BC=12cm,
∴.
∵CD2+AC2=82+152=172=AD2,
∴∠ACD=90°,
∴四边形纸片ABCD的面积=S△ABC+S△ACD
=54+60
=114(cm2).
所以这张纸片的面积为114cm2.
【点评】本题考查了勾股定理及其逆定理,三角形的面积,熟记定理是解题的关键.
10.(2024秋 淮阳区期末)已知,如图在△ABC中,BC=6,AC=8,DE⊥AB,DE=7,△ABE的面积为35,求△ACB的面积.
【考点】勾股定理的逆定理;三角形的面积.
【专题】等腰三角形与直角三角形.
【答案】见试题解答内容
【分析】根据三角形面积求出AB,推出AC、BC的平方和等于AB的平方,求出∠C=90°,根据三角形面积公式求出即可.
【解答】解:∵DE=7,△ABE的面积为35,
∴AB×7=35,
∴AB=10,
∵BC=6,AC=8,
∴AC2+BC2=AB2,
∴∠C=90°,
∴S△ABC6×8=24.
【点评】本题考查了三角形的面积,勾股定理的逆定理的应用,解此题的关键是求出△ABC是直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.夯实基础 勾股定理及其逆定理
一.选择题(共5小题)
1.(2024秋 沙坪坝区校级期中)如图所示的正方形网格中,A、B、C三点均在正方形格点上,则∠BAC的大小是( )
A.30° B.60° C.75° D.90°
2.(2024秋 建邺区校级期中)在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列条件能判断△ABC为直角三角形的是( )
A.c2=a2﹣b2 B.∠A:∠B:∠C=3:4:5
C.a:b:c=7:40:41 D.∠A=40°,∠B=70°
3.(2024秋 宿城区期中)如图,△ABC的顶点都在边长为1的正方形网格的格点上,CD⊥AB于点D,则CD的长是( )
A. B.4 C. D.
4.(2024秋 高陵区期中)如图,在△ABC中,∠B=90°,AC=10,AB=6,求BC的长是( )
A.5 B.8 C.4 D.7
5.(2024秋 江阴市期中)如图,在△ABC中,∠C=90°,AC=8,BC=6,以AB为一条边向三角形外部作正方形,则正方形的面积是( )
A.100 B.80 C.48 D.24
二.解答题(共5小题)
6.(2024秋 深圳期中)如图,已知等腰△ABC的底边BC=13,D是腰AB上一点,且CD=5,BD=12.
(1)BD与AC垂直吗?请说明理由.
(2)求AD的长.
7.(2024秋 九原区期中)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,AB=13,BC=5,求AC、CD的长.
8.(2024秋 惠山区期中)水利是农业的命脉,开远民间历来重视兴修水利,坝区明代即已筑堰修渠,开通东沟、西沟,引泸江、南洞水灌溉农田,经历代不断修拓完善,成为城郊灌溉干渠.这些沟渠凝聚了一代又一代开远人的智慧和心血,历经岁月磨砺、时光雕琢,成为最美的风景,在开远东沟的一侧有一个花卉基地,基地到东沟原有两个取水点A,B,其中AB=AC,为方便花卉基地取水,决定在东沟新建一个取水点D(A、D、B在同一条直线上),并新修一条路CD,测得BC=39m,CD=36m,BD=15m.
(1)求证:CD⊥AB;
(2)求新路CD比原来的路AC少多少米.
9.(2024秋 碑林区校级期中)如图,有一张四边形纸片ABCD,AB⊥BC.经测得AB=9cm,BC=12cm,CD=8cm,AD=17cm,求这张纸片的面积.
10.(2024秋 淮阳区期末)已知,如图在△ABC中,BC=6,AC=8,DE⊥AB,DE=7,△ABE的面积为35,求△ACB的面积.
预习衔接.夯实基础 勾股定理及其逆定理
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 沙坪坝区校级期中)如图所示的正方形网格中,A、B、C三点均在正方形格点上,则∠BAC的大小是( )
A.30° B.60° C.75° D.90°
【考点】勾股定理的逆定理;勾股定理.
【专题】等腰三角形与直角三角形;运算能力.
【答案】D
【分析】利用勾股定理的逆定理证明△ABC是直角三角形,从而可得∠BAC=90°,即可解答.
【解答】解:由题意得:AB2=22+42=20,AC2=12+22=5,BC2=32+42=25,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
∴∠BAC=90°,
故选:D.
【点评】本题考查了勾股定理,勾股定理的逆定理,熟练掌握勾股定理以及勾股定理的逆定理是解题的关键.
2.(2024秋 建邺区校级期中)在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列条件能判断△ABC为直角三角形的是( )
A.c2=a2﹣b2 B.∠A:∠B:∠C=3:4:5
C.a:b:c=7:40:41 D.∠A=40°,∠B=70°
【考点】勾股定理的逆定理;三角形内角和定理.
【专题】等腰三角形与直角三角形;推理能力.
【答案】A
【分析】根据勾股定理和三角形内角和定理对各选项进行逐一判断即可.
【解答】解:A、∵c2=a2﹣b2,
∴c2+b2=a2,
∴△ABC是直角三角形,符合题意;
B、∵∠A:∠B:∠C=3:4:5,∠A+∠B+∠C=180°,
∴最大角∠C180°=75°,
∴△ABC不是直角三角形,不符合题意;
C、∵72+402≠412,
∴△ABC不是直角三角形,不符合题意;
D、∵∠A=40°,∠B=70°,
∴∠C=180°﹣40°﹣70°=70°,
∴△ABC不是直角三角形,不符合题意.
故选:A.
【点评】本题考查的是勾股定理的逆定理及三角形内角和定理,熟知以上知识是解题的关键.
3.(2024秋 宿城区期中)如图,△ABC的顶点都在边长为1的正方形网格的格点上,CD⊥AB于点D,则CD的长是( )
A. B.4 C. D.
【考点】勾股定理.
【专题】等腰三角形与直角三角形;运算能力;推理能力.
【答案】A
【分析】通过勾股定理求出AB的长度,利用面积割补法求出△ABC的面积,再利用等面积求出CD即可.
【解答】解:如图,由勾股定理得 AB5,
∵S△ABC=S长方形CGHK﹣S△CKA﹣S△ABH﹣S△CBG=206﹣2,
又∵S△ABCAB CD,
∴5×CD,
∴CD,
故选:A.
【点评】本题考查了勾股定理,三角形的面积,熟练掌握勾股定理是解题的关键.
4.(2024秋 高陵区期中)如图,在△ABC中,∠B=90°,AC=10,AB=6,求BC的长是( )
A.5 B.8 C.4 D.7
【考点】勾股定理.
【专题】等腰三角形与直角三角形;几何直观;推理能力.
【答案】B
【分析】根据勾股定理得到AB2+BC2=AC2,代入计算即可得BC的值.
【解答】解:在△ABC中,∠B=90°,AC=10,AB=6,
由勾股定理得:AB2+BC2=AC2,
∴6+BC2=102,
∴BC=8(负值舍去),
故选:B.
【点评】本题考查了勾股定理,解答本题的关键是熟练运用数形结合的思想解决问题.
5.(2024秋 江阴市期中)如图,在△ABC中,∠C=90°,AC=8,BC=6,以AB为一条边向三角形外部作正方形,则正方形的面积是( )
A.100 B.80 C.48 D.24
【考点】勾股定理.
【专题】等腰三角形与直角三角形;运算能力;推理能力.
【答案】A
【分析】根据勾股定理和正方形的面积公式即可得到结论.
【解答】解:在△ABC中,∠C=90°,AC=8,BC=6,
∴AB2=AC2+BC2=82+62=100,
∴正方形的面积=AB2=100,
故选:A.
【点评】本题考查了勾股定理、正方形的面积计算等知识,熟练掌握勾股定理是解题的关键.
二.解答题(共5小题)
6.(2024秋 深圳期中)如图,已知等腰△ABC的底边BC=13,D是腰AB上一点,且CD=5,BD=12.
(1)BD与AC垂直吗?请说明理由.
(2)求AD的长.
【考点】勾股定理的逆定理;等腰三角形的性质;勾股定理.
【专题】等腰三角形与直角三角形;推理能力.
【答案】(1)垂直,理由见解析;
(2)11.9.
【分析】(1)由BC=13,CD=5,BD=12得出△BCD是直角三角形,故可得出BD⊥AC;
(2)设AD=x,则AC=AB=x+CD=x+5,再由勾股定理求出x的值即可.
【解答】解:(1)垂直,理由:
∵BC=13,CD=5,BD=12,132=52+122,
∴BC2=CD2+BD2,
∴△BDC为直角三角形且∠BDC=90°,
∴BD与AC垂直;
(2)由(1)知,BD⊥AC,
∵等腰△ABC的底边BC=13,D是腰AB上一点,且CD=5,BD=12,
∴设AD=x,则AC=AB=x+CD=x+5,
∴AD2+BD2=AB2,即x2+122=(x+5)2,
解得x=11.9,
∴AD=11.9.
【点评】此题考查等腰三角形的性质、勾股定理以及逆定理的应用,解题的关键是掌握以上知识.
7.(2024秋 九原区期中)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,AB=13,BC=5,求AC、CD的长.
【考点】勾股定理.
【专题】等腰三角形与直角三角形;推理能力.
【答案】.
【分析】在Rt△ABC中,勾股定理求得AC的长,进而等面积法求得CD,即可求解.
【解答】解:在Rt△ABC中,∠ACB=90°
12,
∵∠ACB=90°,CD⊥AB,
∴,
∴.
【点评】本题考查了勾股定理,熟练掌握勾股定理是解题的关键.
8.(2024秋 惠山区期中)水利是农业的命脉,开远民间历来重视兴修水利,坝区明代即已筑堰修渠,开通东沟、西沟,引泸江、南洞水灌溉农田,经历代不断修拓完善,成为城郊灌溉干渠.这些沟渠凝聚了一代又一代开远人的智慧和心血,历经岁月磨砺、时光雕琢,成为最美的风景,在开远东沟的一侧有一个花卉基地,基地到东沟原有两个取水点A,B,其中AB=AC,为方便花卉基地取水,决定在东沟新建一个取水点D(A、D、B在同一条直线上),并新修一条路CD,测得BC=39m,CD=36m,BD=15m.
(1)求证:CD⊥AB;
(2)求新路CD比原来的路AC少多少米.
【考点】勾股定理的逆定理;两点间的距离.
【专题】等腰三角形与直角三角形;推理能力.
【答案】(1)证明见解析;
(2)14.7米.
【分析】(1)根据勾股定理的逆定理解答即可;
(2)设AC=x m,则AD=(x﹣15)m,在直角△ACD中根据勾股定理求出x的值,进而可得出结论.
【解答】(1)证明:∵BC=39m,CD=36m,BD=15m,362+152=392,
∴CD2+BD2=CB2,
∴△CDB为直角三角形,
∴CD⊥AB;
(2)解:设AC=x m,则AD=(x﹣15)m,
∵CD⊥AB,∠ADC=90°,
∴CD2+AD2=AC2,即362+(x﹣15)2=x2,
解得x=50.7,
∴AC﹣CD=50.7﹣36=14.7(m),
答:新路CD比原来的路AC少14.7米.
【点评】此题考查了勾股定理的逆定理,两点间的距离,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解题的关键.
9.(2024秋 碑林区校级期中)如图,有一张四边形纸片ABCD,AB⊥BC.经测得AB=9cm,BC=12cm,CD=8cm,AD=17cm,求这张纸片的面积.
【考点】勾股定理的逆定理;勾股定理.
【专题】等腰三角形与直角三角形;推理能力.
【答案】114cm2.
【分析】根据勾股定理逆定理证得∠ACD=90°,由于四边形纸片ABCD的面积=S△ABC+S△ACD,根据三角形的面积公式即可求得结论.
【解答】解:如图,连接AC,
在Rt△ABC中,AB⊥BC,AB=9cm,BC=12cm,
∴.
∵CD2+AC2=82+152=172=AD2,
∴∠ACD=90°,
∴四边形纸片ABCD的面积=S△ABC+S△ACD
=54+60
=114(cm2).
所以这张纸片的面积为114cm2.
【点评】本题考查了勾股定理及其逆定理,三角形的面积,熟记定理是解题的关键.
10.(2024秋 淮阳区期末)已知,如图在△ABC中,BC=6,AC=8,DE⊥AB,DE=7,△ABE的面积为35,求△ACB的面积.
【考点】勾股定理的逆定理;三角形的面积.
【专题】等腰三角形与直角三角形.
【答案】见试题解答内容
【分析】根据三角形面积求出AB,推出AC、BC的平方和等于AB的平方,求出∠C=90°,根据三角形面积公式求出即可.
【解答】解:∵DE=7,△ABE的面积为35,
∴AB×7=35,
∴AB=10,
∵BC=6,AC=8,
∴AC2+BC2=AB2,
∴∠C=90°,
∴S△ABC6×8=24.
【点评】本题考查了三角形的面积,勾股定理的逆定理的应用,解此题的关键是求出△ABC是直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
