13.2勾股定理的应用(预习衔接.夯实基础.含解析)-2025-2026学年八年级上册数学华东师大版(2024)
文档属性
| 名称 | 13.2勾股定理的应用(预习衔接.夯实基础.含解析)-2025-2026学年八年级上册数学华东师大版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 453.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 21:27:49 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
预习衔接.夯实基础 勾股定理的应用
一.选择题(共5小题)
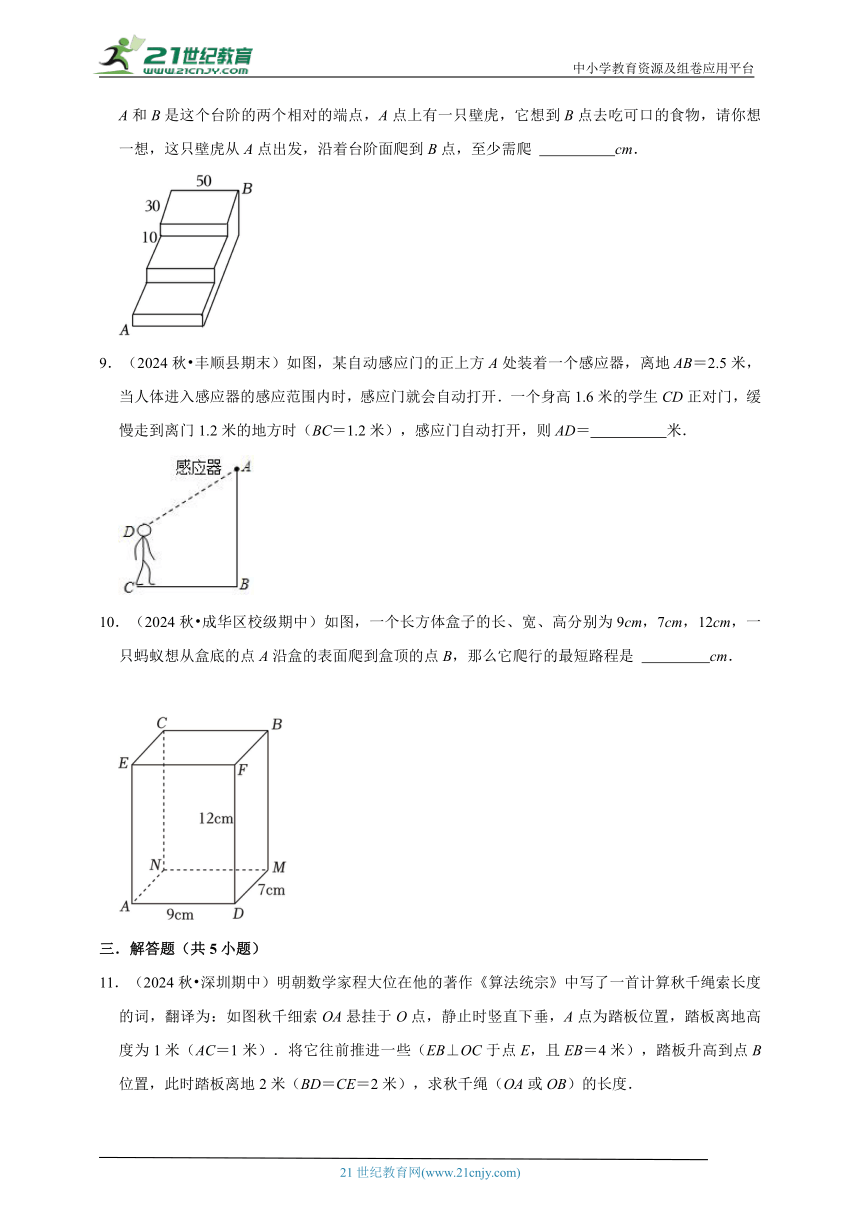
1.(2024秋 成都期中)一架长5m的梯子,如图那样斜靠在一面墙上,梯子的底端离墙1.4m,如果梯子的顶端下滑0.8m,那么他的底部滑行了( )
A.0.8m B.1m C.1.2m D.1.6m
2.(2024秋 昆都仑区校级期中)如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为( )cm(杯壁厚度不计).
A.22cm B.21cm C.20cm D.27cm
3.(2024秋 城阳区期末)如图,四边形ABCD是长方形地面,长AB=10m,宽AD=5m,中间竖有一堵砖墙高MN=1m,一只蚂蚱从点A爬到点C,它必须翻过中间那堵墙,则它至少要走( )
A.13m B.m C.5m D.12m
4.(2024春 齐河县期末)如图,在离水面点A高度为8m的岸上点C处,有人用绳子拉船靠岸,开始时绳子BC的长为17m,此人以1m/s的速度收绳,7s后船移动到点D的位置,则船向岸边移动了( )(假设绳子是直的)
A.9米 B.8米 C.7米 D.6米
5.(2024秋 嵩县期末)勾股定理是人类数学文化的一颗璀璨明珠,是用代数思想解决几何问题最重要的工具,也是数形结合的纽带之一.如图,当秋千静止时,踏板离地的垂直高度BE=1m,将它往前推4m至C处时(即水平距离CD=4m),踏板离地的垂直高度CF=3m,它的绳索始终拉直,则绳索AC的长是( )
A.4m B.5m C.6m D.8m
二.填空题(共5小题)
6.(2024春 汕头期中)如图,圆柱体的高为6cm,底面周长为6cm,在圆柱下底面A处有一只蚂蚁,想吃到和它相对的侧面B处的食物,已知B处距上底2cm,则蚂蚁沿侧面爬行的最短路径是 cm.
7.(2024秋 宝安区期中)如图,一天傍晚,小方和家人去小区遛狗,小方观察发现,她站直身体时,牵绳的手离地面高度为AB=1.3米,小狗的高CD=0.3米,小狗与小方的距离AC=2.4米.(绳子一直是直的)牵狗绳BD的长 .
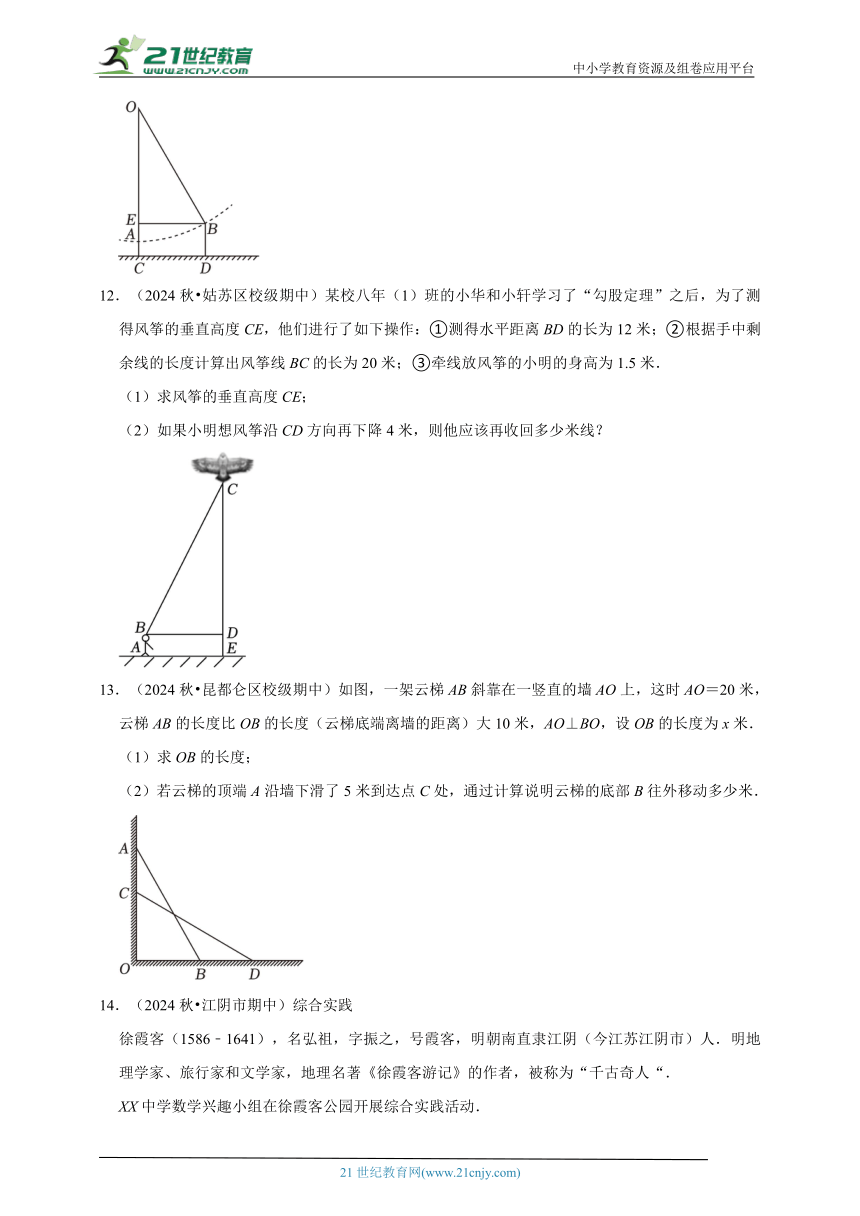
8.(2024秋 荥阳市期中)如图是一个三级台阶,它的每一级的长、宽和高分别是50cm,30cm,10cm,A和B是这个台阶的两个相对的端点,A点上有一只壁虎,它想到B点去吃可口的食物,请你想一想,这只壁虎从A点出发,沿着台阶面爬到B点,至少需爬 cm.
9.(2024秋 丰顺县期末)如图,某自动感应门的正上方A处装着一个感应器,离地AB=2.5米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),感应门自动打开,则AD= 米.
10.(2024秋 成华区校级期中)如图,一个长方体盒子的长、宽、高分别为9cm,7cm,12cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,那么它爬行的最短路程是 cm.
三.解答题(共5小题)
11.(2024秋 深圳期中)明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词,翻译为:如图秋千细索OA悬挂于O点,静止时竖直下垂,A点为踏板位置,踏板离地高度为1米(AC=1米).将它往前推进一些(EB⊥OC于点E,且EB=4米),踏板升高到点B位置,此时踏板离地2米(BD=CE=2米),求秋千绳(OA或OB)的长度.
12.(2024秋 姑苏区校级期中)某校八年(1)班的小华和小轩学习了“勾股定理”之后,为了测得风筝的垂直高度CE,他们进行了如下操作:①测得水平距离BD的长为12米;②根据手中剩余线的长度计算出风筝线BC的长为20米;③牵线放风筝的小明的身高为1.5米.
(1)求风筝的垂直高度CE;
(2)如果小明想风筝沿CD方向再下降4米,则他应该再收回多少米线?
13.(2024秋 昆都仑区校级期中)如图,一架云梯AB斜靠在一竖直的墙AO上,这时AO=20米,云梯AB的长度比OB的长度(云梯底端离墙的距离)大10米,AO⊥BO,设OB的长度为x米.
(1)求OB的长度;
(2)若云梯的顶端A沿墙下滑了5米到达点C处,通过计算说明云梯的底部B往外移动多少米.
14.(2024秋 江阴市期中)综合实践
徐霞客(1586﹣1641),名弘祖,字振之,号霞客,明朝南直隶江阴(今江苏江阴市)人.明地理学家、旅行家和文学家,地理名著《徐霞客游记》的作者,被称为“千古奇人“.
XX中学数学兴趣小组在徐霞客公园开展综合实践活动.
主题:检测雕塑(如图)底座正面的边AD和边BC是否分别垂直于底边CD.
素材:一个雕塑,一把卷尺
步骤1:利用卷尺测量边AD,底边CD的长度,并测量出点A,C之间的距离;
步骤2:通过计算验证底座正面的边AD和边BC是否分别垂直于底边CD.
解决问题:
通过测量得到边AD的长是60厘米,边CD的长是80厘米,AC的长是100厘米,边AD垂直于边CD吗?为什么?
15.(2024秋 城阳区期中)如图,五一假期,数学兴趣小组的同学来到城阳区澜湾艺术公园露营、放风筝,他们想知道风筝离地面的垂直高度,于是利用所学数学知识来解决实际问题,实践报告如下:
活动课题 探究风筝离地面的垂直高度
活动工具 直角三角板、皮尺等
活动过程 小组成员测量了相关数据,并画出了如图所示的示意图,测得水平距离BC的长为15米,根据手中剩余线的长度计算出风筝线AB的长为17米,牵线放风筝的手到地面的距离为1.5米.(即CD=BE=1.5米)
问题解决 (1)求风筝离地面的垂直高度. (2)如果小明想要把风筝沿射线DA方向再上升12米,且BC长度不变,那么他应该再放出多少米线?
请你帮助兴趣小组解决以上问题.
预习衔接.夯实基础 勾股定理的应用
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 成都期中)一架长5m的梯子,如图那样斜靠在一面墙上,梯子的底端离墙1.4m,如果梯子的顶端下滑0.8m,那么他的底部滑行了( )
A.0.8m B.1m C.1.2m D.1.6m
【考点】勾股定理的应用.
【专题】等腰三角形与直角三角形;运算能力;应用意识.
【答案】D
【分析】根据梯子长度不会变这个等量关系,根据BC求AC,根据AD、AC求CD,根据CD计算CE,根据CE,BC计算BE,即可解题.
【解答】解:由题意知AB=DE=5m,BC=1.4m,AD=0.8m,
在Rt△ABC中,AC为直角边,
∴AC4.8(m),
已知AD=0.8m,则CD=4.8﹣0.8=4(m),
在Rt△CDE中,CE为直角边,
∴CE3(m),
∴BE=3﹣1.4=1.6(m),
故选:D.
【点评】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.
2.(2024秋 昆都仑区校级期中)如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为( )cm(杯壁厚度不计).
A.22cm B.21cm C.20cm D.27cm
【考点】平面展开﹣最短路径问题.
【专题】展开与折叠;推理能力.
【答案】C
【分析】将杯子侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.
【解答】解:如图:
将杯子侧面展开,作A关于EF的对称点A′,
连接A′B,交EF于点F,此时点A′、F、B在同一条直线上,
则AF+BF为蚂蚁从外壁A处到内壁B处的最短距离,即A′B的长度,
依题意,A′D=32÷2=16(cm),BD=3+(14﹣5)=12(cm)
此时.
∴蚂蚁从外壁A处到内壁B处的最短距离为20cm,
故选:C.
【点评】本题考查了平面展开﹣﹣﹣最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.
3.(2024秋 城阳区期末)如图,四边形ABCD是长方形地面,长AB=10m,宽AD=5m,中间竖有一堵砖墙高MN=1m,一只蚂蚱从点A爬到点C,它必须翻过中间那堵墙,则它至少要走( )
A.13m B.m C.5m D.12m
【考点】平面展开﹣最短路径问题.
【专题】等腰三角形与直角三角形;应用意识.
【答案】A
【分析】连接AC,利用勾股定理求出AC的长,再把中间的墙平面展开,使原来的矩形长度增加而宽度不变,求出新矩形的对角线长即可.
【解答】解:如图所示,将图展开,图形长度增加2MN,
原图长度增加2米,则AB=10+2=12(m),
连接AC,
∵四边形ABCD是长方形,AB=12m,宽AD=5m,
∴AC13(m),
∴蚂蚱从A点爬到C点,它至少要走13m的路程.
故选:A.
【点评】本题考查的是平面展开最短路线问题及勾股定理,根据题意画出图形是解答此题的关键.
4.(2024春 齐河县期末)如图,在离水面点A高度为8m的岸上点C处,有人用绳子拉船靠岸,开始时绳子BC的长为17m,此人以1m/s的速度收绳,7s后船移动到点D的位置,则船向岸边移动了( )(假设绳子是直的)
A.9米 B.8米 C.7米 D.6米
【考点】勾股定理的应用.
【专题】等腰三角形与直角三角形;运算能力;应用意识.
【答案】A
【分析】由勾股定理求出AB=15m,再由勾股定理求出AD=6m,即可解决问题.
【解答】解:在Rt△ABC中,∠CAB=90°,BC=17m,AC=8m,
∴AB15(m),
∵此人以1m/s的速度收绳,7s后船移动到点D的位置,
∴CD=17﹣1×7=10(m),
在Rt△ACD中,由勾股定理得:AD6(m),
∴BD=AB﹣AD=15﹣6=9(m),
即船向岸边移动了9m,
故选:A.
【点评】本题考查勾股定理的运用,熟练掌握勾股定理,求出AB和AD的长是解题的关键.
5.(2024秋 嵩县期末)勾股定理是人类数学文化的一颗璀璨明珠,是用代数思想解决几何问题最重要的工具,也是数形结合的纽带之一.如图,当秋千静止时,踏板离地的垂直高度BE=1m,将它往前推4m至C处时(即水平距离CD=4m),踏板离地的垂直高度CF=3m,它的绳索始终拉直,则绳索AC的长是( )
A.4m B.5m C.6m D.8m
【考点】勾股定理的应用.
【专题】解直角三角形及其应用;运算能力;推理能力.
【答案】B
【分析】设AC的长为x,则AB=AC=x m,故AD=AB﹣BD=(x﹣2)m.在直角△ADC中利用勾股定理即可求解.
【解答】解:由题意可知,CF=3m,BE=1m,
∴BD=2m.
设AC的长为x m,则AB=AC=x (m),
所以AD=AB﹣BD=(x﹣2)m.
在直角△ADC中,AD2+CD2=AC2,即(x﹣2)2+42=x2,
解得:x=5.
故选:B.
【点评】本题考查勾股定理的实际应用.找到直角三角形,利用勾股定理即可.
二.填空题(共5小题)
6.(2024春 汕头期中)如图,圆柱体的高为6cm,底面周长为6cm,在圆柱下底面A处有一只蚂蚁,想吃到和它相对的侧面B处的食物,已知B处距上底2cm,则蚂蚁沿侧面爬行的最短路径是 5 cm.
【考点】平面展开﹣最短路径问题.
【专题】展开与折叠;运算能力.
【答案】5.
【分析】先把圆柱的侧面展开得其侧面展开图,则A,H所在的长方形的长为圆柱的高6cm,宽为底面圆周长的一半,BC=CH﹣BH=4cm,蚂蚁经过的最短距离为连接A,B的线段长,由勾股定理求得AB的长.
【解答】解:如图,将圆柱的侧面沿过A点的一条母线剪开,
连接AB,则线段AB的长就是蚂蚁爬行的最短距离,C、H分别是AE、DF的中点,
∵底面周长是6cm,
∴AC=3cm,
∵CH=6cm,BH=2cm,
∴BC=4cm,
∴,
故答案为:5.
【点评】本题考查平面展开﹣最短路径问题,勾股定理的应用,正确利用展开图进行计算是解题关键.
7.(2024秋 宝安区期中)如图,一天傍晚,小方和家人去小区遛狗,小方观察发现,她站直身体时,牵绳的手离地面高度为AB=1.3米,小狗的高CD=0.3米,小狗与小方的距离AC=2.4米.(绳子一直是直的)牵狗绳BD的长 2.6米 .
【考点】勾股定理的应用.
【专题】等腰三角形与直角三角形;应用意识.
【答案】2.6米.
【分析】过点D作DE⊥AB于点E,可得DE=AC=2.4,AE=CD=0.3,DE=1,再根据勾股定理求解即可
【解答】解:如图,过点D作DE⊥AB于点E,
则AE=CD=0.3米,DE=AC=2.4米,
∴BE=AB﹣AE=1米,
∴BD2.6(米).
所以此时牵狗绳BD的长为2.6米.
故答案为:2.6米.
【点评】本题考查勾股定理的应用,理解并掌握勾股定理是解决问题的关键.
8.(2024秋 荥阳市期中)如图是一个三级台阶,它的每一级的长、宽和高分别是50cm,30cm,10cm,A和B是这个台阶的两个相对的端点,A点上有一只壁虎,它想到B点去吃可口的食物,请你想一想,这只壁虎从A点出发,沿着台阶面爬到B点,至少需爬 130 cm.
【考点】平面展开﹣最短路径问题.
【专题】等腰三角形与直角三角形;应用意识.
【答案】130.
【分析】此类题目只需要将其展开便可直观的得出解题思路.将台阶展开得到的是一个矩形,蚂蚁要从B点到A点的最短距离,便是矩形的对角线,利用勾股定理即可解出答案.
【解答】解:将台阶展开,如图,
∵因为BC=30×3+10×3=120,AC=50,
∴AB2=AC2+BC2=16900,
∴AB=130(cm),
∴壁虎爬行的最短线路为130cm.
故答案为:130.
【点评】本题主要考查了平面展开﹣最短路径问题,勾股定理,解题关键是画出求A到B的最短路径的展开图.
9.(2024秋 丰顺县期末)如图,某自动感应门的正上方A处装着一个感应器,离地AB=2.5米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),感应门自动打开,则AD= 1.5 米.
【考点】勾股定理的应用.
【专题】等腰三角形与直角三角形;运算能力.
【答案】见试题解答内容
【分析】过点D作DE⊥AB于点E,构造Rt△ADE,利用勾股定理求得AD的长度即可.
【解答】解:如图,过点D作DE⊥AB于点E,
∵AB=2.5米,BE=CD=1.6米,ED=BC=1.2米,则AE=AB﹣BE=2.5﹣1.6=0.9(米).
在Rt△ADE中,由勾股定理得到:AD1.5(米)
故答案为:1.5.
【点评】本题考查了勾股定理的应用,解题的关键是作出辅助线,构造直角三角形,利用勾股定理求得线段AD的长度.
10.(2024秋 成华区校级期中)如图,一个长方体盒子的长、宽、高分别为9cm,7cm,12cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,那么它爬行的最短路程是 20 cm.
【考点】平面展开﹣最短路径问题;勾股定理的应用.
【专题】等腰三角形与直角三角形;展开与折叠;推理能力.
【答案】20cm.
【分析】分为三种情况展开,根据勾股定理求出线段AB的长度,再进行比较即可.
【解答】解:①如图1,展开后连接AB,则AB就是在表面上从A到B的最短距离,
在Rt△ABM中,由勾股定理得:AB20(cm);
②如图2,展开后连接AB,则AB就是在表面上从A到B的最短距离,
在Rt△ADB中,由勾股定理得:AB(cm);
③如图3,展开后连接AB,则AB就是在表面上A到B的最短距离,
在Rt△ANB中,由勾股定理得:AB7(cm).
∴蚂蚁爬行的最短路程是20cm.
【点评】本题考查了平面展开﹣最短路线问题和勾股定理等知识点,关键是能画出展开图形并能求出符合条件的最短路线.
三.解答题(共5小题)
11.(2024秋 深圳期中)明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词,翻译为:如图秋千细索OA悬挂于O点,静止时竖直下垂,A点为踏板位置,踏板离地高度为1米(AC=1米).将它往前推进一些(EB⊥OC于点E,且EB=4米),踏板升高到点B位置,此时踏板离地2米(BD=CE=2米),求秋千绳(OA或OB)的长度.
【考点】勾股定理的应用.
【专题】等腰三角形与直角三角形;运算能力;应用意识.
【答案】8.5米.
【分析】设OB=OA=x米,则OE=OA﹣AE=(x﹣1)米,在Rt△OBE中,由勾股定理列出方程,解方程即可.
【解答】解:设OB=OA=x米,
∵AE=CE﹣AC=2﹣1=1(米),
∴OE=OA﹣AE=(x﹣1)米,
在Rt△OBE中,由勾股定理得:OB2=EB2+OE2,
即x2=42+(x﹣1)2,
解得:x=8.5,
答:秋千绳(OA或OB)的长度为8.5米.
【点评】本题主要考查了勾股定理的应用,根据勾股定理列出方程是解题的关键.
12.(2024秋 姑苏区校级期中)某校八年(1)班的小华和小轩学习了“勾股定理”之后,为了测得风筝的垂直高度CE,他们进行了如下操作:①测得水平距离BD的长为12米;②根据手中剩余线的长度计算出风筝线BC的长为20米;③牵线放风筝的小明的身高为1.5米.
(1)求风筝的垂直高度CE;
(2)如果小明想风筝沿CD方向再下降4米,则他应该再收回多少米线?
【考点】勾股定理的应用.
【专题】等腰三角形与直角三角形;运算能力;应用意识.
【答案】(1)风筝的高度CE为17.5米;
(2)他应该再收回(20﹣12)米.
【分析】(1)利用勾股定理求出CD的长,再加上DE的长度,即可求出CE的高度;
(2)根据勾股定理即可得到结论.
【解答】解:(1)在Rt△CDB中,
由勾股定理得,CD2=BC2﹣BD2=202﹣122=256,
所以,CD=16(负值舍去),
所以,CE=CD+DE=16+1.5=17.5(米),
答:风筝的高度CE为17.5米;
(2)如图所示:在DC上取一点M,使CM=4米,连接BM,
由题意得,CM=4米,
∴DM=12米,
在Rt△MDB中,
∴BM12(米),
∴BC﹣BM=(20﹣12)米,
∴他应该再收回(20﹣12)米.
【点评】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.
13.(2024秋 昆都仑区校级期中)如图,一架云梯AB斜靠在一竖直的墙AO上,这时AO=20米,云梯AB的长度比OB的长度(云梯底端离墙的距离)大10米,AO⊥BO,设OB的长度为x米.
(1)求OB的长度;
(2)若云梯的顶端A沿墙下滑了5米到达点C处,通过计算说明云梯的底部B往外移动多少米.
【考点】勾股定理的应用.
【专题】等腰三角形与直角三角形;运算能力;推理能力.
【答案】(1)OB的长度为15米;
(2)云梯的底部B往外移动了5米.
【分析】(1)根据勾股定理得出方程求解即可;
(2)由勾股定理求出OD的长即可得出结论.
【解答】解:(1)由题意知,AB=(x+10)米,
在Rt△AOB中,由勾股定理得,
OB2+OA2=AB2,
即x2+202=(x+10)2,
解得x=15,
∴OB的长度为15米;
(2)由题意知,OC=AO﹣AC=20﹣5=15(米),CD=AB=25米,
在Rt△OCD中,由勾股定理得,
OC2+OD2=CD2,
即152+OD2=252,
解得OD=20米(负值舍去),
∴BD=20﹣15=5(米),
∴云梯的底部B往外移动了5米.
【点评】本题考查了勾股定理的应用,熟记勾股定理是解题的关键.
14.(2024秋 江阴市期中)综合实践
徐霞客(1586﹣1641),名弘祖,字振之,号霞客,明朝南直隶江阴(今江苏江阴市)人.明地理学家、旅行家和文学家,地理名著《徐霞客游记》的作者,被称为“千古奇人“.
XX中学数学兴趣小组在徐霞客公园开展综合实践活动.
主题:检测雕塑(如图)底座正面的边AD和边BC是否分别垂直于底边CD.
素材:一个雕塑,一把卷尺
步骤1:利用卷尺测量边AD,底边CD的长度,并测量出点A,C之间的距离;
步骤2:通过计算验证底座正面的边AD和边BC是否分别垂直于底边CD.
解决问题:
通过测量得到边AD的长是60厘米,边CD的长是80厘米,AC的长是100厘米,边AD垂直于边CD吗?为什么?
【考点】勾股定理的应用;有理数的减法.
【专题】三角形;等腰三角形与直角三角形;运算能力.
【答案】垂直,理由见解析.
【分析】根据勾股定理逆定理进行检验即可;
【解答】解:垂直.
理由如下:∵AD=60厘米,CD=80厘米,AC=100厘米,
而602+802=1002,
∴AD2+CD2=AC2,
∴△ACD是直角三角形,
∴AD⊥CD.
【点评】本题考查的是勾股定理的应用,熟记勾股定理是解题的关键.
15.(2024秋 城阳区期中)如图,五一假期,数学兴趣小组的同学来到城阳区澜湾艺术公园露营、放风筝,他们想知道风筝离地面的垂直高度,于是利用所学数学知识来解决实际问题,实践报告如下:
活动课题 探究风筝离地面的垂直高度
活动工具 直角三角板、皮尺等
活动过程 小组成员测量了相关数据,并画出了如图所示的示意图,测得水平距离BC的长为15米,根据手中剩余线的长度计算出风筝线AB的长为17米,牵线放风筝的手到地面的距离为1.5米.(即CD=BE=1.5米)
问题解决 (1)求风筝离地面的垂直高度. (2)如果小明想要把风筝沿射线DA方向再上升12米,且BC长度不变,那么他应该再放出多少米线?
请你帮助兴趣小组解决以上问题.
【考点】勾股定理的应用.
【专题】等腰三角形与直角三角形;运算能力;应用意识.
【答案】(1)风筝离地面的垂直高度为9.5米;
(2)他应该再放出8米长的线.
【分析】(1)在Rt△ABC中,利用勾股定理求出的AC长,即可得到结论;
(2)在Rt△A′BC中,根据勾股定理求出A′B,即可得到结论.
【解答】解:(1)在Rt△ABC中,∠ACB=90°,BC=15米,AB=17米,
由勾股定理得:AC8(米),
∴AD=AC+CD=8+1.5=9.5(米),
答:风筝离地面的垂直高度为9.5米;
(2)如图,当风筝沿DA方向再上升12米时,A'C=12+8=20(米),
在Rt△A′BC中,∠A'CB=90°,BC=15米,
由勾股定理得:A′B25(米),
∴A'B﹣AB=25﹣17=8(米),
答:小明应该再放出8米长的线.
【点评】本题考查了勾股定理的应用,熟练掌握勾股定理,求出AC、A'B的长是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.夯实基础 勾股定理的应用
一.选择题(共5小题)
1.(2024秋 成都期中)一架长5m的梯子,如图那样斜靠在一面墙上,梯子的底端离墙1.4m,如果梯子的顶端下滑0.8m,那么他的底部滑行了( )
A.0.8m B.1m C.1.2m D.1.6m
2.(2024秋 昆都仑区校级期中)如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为( )cm(杯壁厚度不计).
A.22cm B.21cm C.20cm D.27cm
3.(2024秋 城阳区期末)如图,四边形ABCD是长方形地面,长AB=10m,宽AD=5m,中间竖有一堵砖墙高MN=1m,一只蚂蚱从点A爬到点C,它必须翻过中间那堵墙,则它至少要走( )
A.13m B.m C.5m D.12m
4.(2024春 齐河县期末)如图,在离水面点A高度为8m的岸上点C处,有人用绳子拉船靠岸,开始时绳子BC的长为17m,此人以1m/s的速度收绳,7s后船移动到点D的位置,则船向岸边移动了( )(假设绳子是直的)
A.9米 B.8米 C.7米 D.6米
5.(2024秋 嵩县期末)勾股定理是人类数学文化的一颗璀璨明珠,是用代数思想解决几何问题最重要的工具,也是数形结合的纽带之一.如图,当秋千静止时,踏板离地的垂直高度BE=1m,将它往前推4m至C处时(即水平距离CD=4m),踏板离地的垂直高度CF=3m,它的绳索始终拉直,则绳索AC的长是( )
A.4m B.5m C.6m D.8m
二.填空题(共5小题)
6.(2024春 汕头期中)如图,圆柱体的高为6cm,底面周长为6cm,在圆柱下底面A处有一只蚂蚁,想吃到和它相对的侧面B处的食物,已知B处距上底2cm,则蚂蚁沿侧面爬行的最短路径是 cm.
7.(2024秋 宝安区期中)如图,一天傍晚,小方和家人去小区遛狗,小方观察发现,她站直身体时,牵绳的手离地面高度为AB=1.3米,小狗的高CD=0.3米,小狗与小方的距离AC=2.4米.(绳子一直是直的)牵狗绳BD的长 .
8.(2024秋 荥阳市期中)如图是一个三级台阶,它的每一级的长、宽和高分别是50cm,30cm,10cm,A和B是这个台阶的两个相对的端点,A点上有一只壁虎,它想到B点去吃可口的食物,请你想一想,这只壁虎从A点出发,沿着台阶面爬到B点,至少需爬 cm.
9.(2024秋 丰顺县期末)如图,某自动感应门的正上方A处装着一个感应器,离地AB=2.5米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),感应门自动打开,则AD= 米.
10.(2024秋 成华区校级期中)如图,一个长方体盒子的长、宽、高分别为9cm,7cm,12cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,那么它爬行的最短路程是 cm.
三.解答题(共5小题)
11.(2024秋 深圳期中)明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词,翻译为:如图秋千细索OA悬挂于O点,静止时竖直下垂,A点为踏板位置,踏板离地高度为1米(AC=1米).将它往前推进一些(EB⊥OC于点E,且EB=4米),踏板升高到点B位置,此时踏板离地2米(BD=CE=2米),求秋千绳(OA或OB)的长度.
12.(2024秋 姑苏区校级期中)某校八年(1)班的小华和小轩学习了“勾股定理”之后,为了测得风筝的垂直高度CE,他们进行了如下操作:①测得水平距离BD的长为12米;②根据手中剩余线的长度计算出风筝线BC的长为20米;③牵线放风筝的小明的身高为1.5米.
(1)求风筝的垂直高度CE;
(2)如果小明想风筝沿CD方向再下降4米,则他应该再收回多少米线?
13.(2024秋 昆都仑区校级期中)如图,一架云梯AB斜靠在一竖直的墙AO上,这时AO=20米,云梯AB的长度比OB的长度(云梯底端离墙的距离)大10米,AO⊥BO,设OB的长度为x米.
(1)求OB的长度;
(2)若云梯的顶端A沿墙下滑了5米到达点C处,通过计算说明云梯的底部B往外移动多少米.
14.(2024秋 江阴市期中)综合实践
徐霞客(1586﹣1641),名弘祖,字振之,号霞客,明朝南直隶江阴(今江苏江阴市)人.明地理学家、旅行家和文学家,地理名著《徐霞客游记》的作者,被称为“千古奇人“.
XX中学数学兴趣小组在徐霞客公园开展综合实践活动.
主题:检测雕塑(如图)底座正面的边AD和边BC是否分别垂直于底边CD.
素材:一个雕塑,一把卷尺
步骤1:利用卷尺测量边AD,底边CD的长度,并测量出点A,C之间的距离;
步骤2:通过计算验证底座正面的边AD和边BC是否分别垂直于底边CD.
解决问题:
通过测量得到边AD的长是60厘米,边CD的长是80厘米,AC的长是100厘米,边AD垂直于边CD吗?为什么?
15.(2024秋 城阳区期中)如图,五一假期,数学兴趣小组的同学来到城阳区澜湾艺术公园露营、放风筝,他们想知道风筝离地面的垂直高度,于是利用所学数学知识来解决实际问题,实践报告如下:
活动课题 探究风筝离地面的垂直高度
活动工具 直角三角板、皮尺等
活动过程 小组成员测量了相关数据,并画出了如图所示的示意图,测得水平距离BC的长为15米,根据手中剩余线的长度计算出风筝线AB的长为17米,牵线放风筝的手到地面的距离为1.5米.(即CD=BE=1.5米)
问题解决 (1)求风筝离地面的垂直高度. (2)如果小明想要把风筝沿射线DA方向再上升12米,且BC长度不变,那么他应该再放出多少米线?
请你帮助兴趣小组解决以上问题.
预习衔接.夯实基础 勾股定理的应用
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 成都期中)一架长5m的梯子,如图那样斜靠在一面墙上,梯子的底端离墙1.4m,如果梯子的顶端下滑0.8m,那么他的底部滑行了( )
A.0.8m B.1m C.1.2m D.1.6m
【考点】勾股定理的应用.
【专题】等腰三角形与直角三角形;运算能力;应用意识.
【答案】D
【分析】根据梯子长度不会变这个等量关系,根据BC求AC,根据AD、AC求CD,根据CD计算CE,根据CE,BC计算BE,即可解题.
【解答】解:由题意知AB=DE=5m,BC=1.4m,AD=0.8m,
在Rt△ABC中,AC为直角边,
∴AC4.8(m),
已知AD=0.8m,则CD=4.8﹣0.8=4(m),
在Rt△CDE中,CE为直角边,
∴CE3(m),
∴BE=3﹣1.4=1.6(m),
故选:D.
【点评】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.
2.(2024秋 昆都仑区校级期中)如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为( )cm(杯壁厚度不计).
A.22cm B.21cm C.20cm D.27cm
【考点】平面展开﹣最短路径问题.
【专题】展开与折叠;推理能力.
【答案】C
【分析】将杯子侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.
【解答】解:如图:
将杯子侧面展开,作A关于EF的对称点A′,
连接A′B,交EF于点F,此时点A′、F、B在同一条直线上,
则AF+BF为蚂蚁从外壁A处到内壁B处的最短距离,即A′B的长度,
依题意,A′D=32÷2=16(cm),BD=3+(14﹣5)=12(cm)
此时.
∴蚂蚁从外壁A处到内壁B处的最短距离为20cm,
故选:C.
【点评】本题考查了平面展开﹣﹣﹣最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.
3.(2024秋 城阳区期末)如图,四边形ABCD是长方形地面,长AB=10m,宽AD=5m,中间竖有一堵砖墙高MN=1m,一只蚂蚱从点A爬到点C,它必须翻过中间那堵墙,则它至少要走( )
A.13m B.m C.5m D.12m
【考点】平面展开﹣最短路径问题.
【专题】等腰三角形与直角三角形;应用意识.
【答案】A
【分析】连接AC,利用勾股定理求出AC的长,再把中间的墙平面展开,使原来的矩形长度增加而宽度不变,求出新矩形的对角线长即可.
【解答】解:如图所示,将图展开,图形长度增加2MN,
原图长度增加2米,则AB=10+2=12(m),
连接AC,
∵四边形ABCD是长方形,AB=12m,宽AD=5m,
∴AC13(m),
∴蚂蚱从A点爬到C点,它至少要走13m的路程.
故选:A.
【点评】本题考查的是平面展开最短路线问题及勾股定理,根据题意画出图形是解答此题的关键.
4.(2024春 齐河县期末)如图,在离水面点A高度为8m的岸上点C处,有人用绳子拉船靠岸,开始时绳子BC的长为17m,此人以1m/s的速度收绳,7s后船移动到点D的位置,则船向岸边移动了( )(假设绳子是直的)
A.9米 B.8米 C.7米 D.6米
【考点】勾股定理的应用.
【专题】等腰三角形与直角三角形;运算能力;应用意识.
【答案】A
【分析】由勾股定理求出AB=15m,再由勾股定理求出AD=6m,即可解决问题.
【解答】解:在Rt△ABC中,∠CAB=90°,BC=17m,AC=8m,
∴AB15(m),
∵此人以1m/s的速度收绳,7s后船移动到点D的位置,
∴CD=17﹣1×7=10(m),
在Rt△ACD中,由勾股定理得:AD6(m),
∴BD=AB﹣AD=15﹣6=9(m),
即船向岸边移动了9m,
故选:A.
【点评】本题考查勾股定理的运用,熟练掌握勾股定理,求出AB和AD的长是解题的关键.
5.(2024秋 嵩县期末)勾股定理是人类数学文化的一颗璀璨明珠,是用代数思想解决几何问题最重要的工具,也是数形结合的纽带之一.如图,当秋千静止时,踏板离地的垂直高度BE=1m,将它往前推4m至C处时(即水平距离CD=4m),踏板离地的垂直高度CF=3m,它的绳索始终拉直,则绳索AC的长是( )
A.4m B.5m C.6m D.8m
【考点】勾股定理的应用.
【专题】解直角三角形及其应用;运算能力;推理能力.
【答案】B
【分析】设AC的长为x,则AB=AC=x m,故AD=AB﹣BD=(x﹣2)m.在直角△ADC中利用勾股定理即可求解.
【解答】解:由题意可知,CF=3m,BE=1m,
∴BD=2m.
设AC的长为x m,则AB=AC=x (m),
所以AD=AB﹣BD=(x﹣2)m.
在直角△ADC中,AD2+CD2=AC2,即(x﹣2)2+42=x2,
解得:x=5.
故选:B.
【点评】本题考查勾股定理的实际应用.找到直角三角形,利用勾股定理即可.
二.填空题(共5小题)
6.(2024春 汕头期中)如图,圆柱体的高为6cm,底面周长为6cm,在圆柱下底面A处有一只蚂蚁,想吃到和它相对的侧面B处的食物,已知B处距上底2cm,则蚂蚁沿侧面爬行的最短路径是 5 cm.
【考点】平面展开﹣最短路径问题.
【专题】展开与折叠;运算能力.
【答案】5.
【分析】先把圆柱的侧面展开得其侧面展开图,则A,H所在的长方形的长为圆柱的高6cm,宽为底面圆周长的一半,BC=CH﹣BH=4cm,蚂蚁经过的最短距离为连接A,B的线段长,由勾股定理求得AB的长.
【解答】解:如图,将圆柱的侧面沿过A点的一条母线剪开,
连接AB,则线段AB的长就是蚂蚁爬行的最短距离,C、H分别是AE、DF的中点,
∵底面周长是6cm,
∴AC=3cm,
∵CH=6cm,BH=2cm,
∴BC=4cm,
∴,
故答案为:5.
【点评】本题考查平面展开﹣最短路径问题,勾股定理的应用,正确利用展开图进行计算是解题关键.
7.(2024秋 宝安区期中)如图,一天傍晚,小方和家人去小区遛狗,小方观察发现,她站直身体时,牵绳的手离地面高度为AB=1.3米,小狗的高CD=0.3米,小狗与小方的距离AC=2.4米.(绳子一直是直的)牵狗绳BD的长 2.6米 .
【考点】勾股定理的应用.
【专题】等腰三角形与直角三角形;应用意识.
【答案】2.6米.
【分析】过点D作DE⊥AB于点E,可得DE=AC=2.4,AE=CD=0.3,DE=1,再根据勾股定理求解即可
【解答】解:如图,过点D作DE⊥AB于点E,
则AE=CD=0.3米,DE=AC=2.4米,
∴BE=AB﹣AE=1米,
∴BD2.6(米).
所以此时牵狗绳BD的长为2.6米.
故答案为:2.6米.
【点评】本题考查勾股定理的应用,理解并掌握勾股定理是解决问题的关键.
8.(2024秋 荥阳市期中)如图是一个三级台阶,它的每一级的长、宽和高分别是50cm,30cm,10cm,A和B是这个台阶的两个相对的端点,A点上有一只壁虎,它想到B点去吃可口的食物,请你想一想,这只壁虎从A点出发,沿着台阶面爬到B点,至少需爬 130 cm.
【考点】平面展开﹣最短路径问题.
【专题】等腰三角形与直角三角形;应用意识.
【答案】130.
【分析】此类题目只需要将其展开便可直观的得出解题思路.将台阶展开得到的是一个矩形,蚂蚁要从B点到A点的最短距离,便是矩形的对角线,利用勾股定理即可解出答案.
【解答】解:将台阶展开,如图,
∵因为BC=30×3+10×3=120,AC=50,
∴AB2=AC2+BC2=16900,
∴AB=130(cm),
∴壁虎爬行的最短线路为130cm.
故答案为:130.
【点评】本题主要考查了平面展开﹣最短路径问题,勾股定理,解题关键是画出求A到B的最短路径的展开图.
9.(2024秋 丰顺县期末)如图,某自动感应门的正上方A处装着一个感应器,离地AB=2.5米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),感应门自动打开,则AD= 1.5 米.
【考点】勾股定理的应用.
【专题】等腰三角形与直角三角形;运算能力.
【答案】见试题解答内容
【分析】过点D作DE⊥AB于点E,构造Rt△ADE,利用勾股定理求得AD的长度即可.
【解答】解:如图,过点D作DE⊥AB于点E,
∵AB=2.5米,BE=CD=1.6米,ED=BC=1.2米,则AE=AB﹣BE=2.5﹣1.6=0.9(米).
在Rt△ADE中,由勾股定理得到:AD1.5(米)
故答案为:1.5.
【点评】本题考查了勾股定理的应用,解题的关键是作出辅助线,构造直角三角形,利用勾股定理求得线段AD的长度.
10.(2024秋 成华区校级期中)如图,一个长方体盒子的长、宽、高分别为9cm,7cm,12cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,那么它爬行的最短路程是 20 cm.
【考点】平面展开﹣最短路径问题;勾股定理的应用.
【专题】等腰三角形与直角三角形;展开与折叠;推理能力.
【答案】20cm.
【分析】分为三种情况展开,根据勾股定理求出线段AB的长度,再进行比较即可.
【解答】解:①如图1,展开后连接AB,则AB就是在表面上从A到B的最短距离,
在Rt△ABM中,由勾股定理得:AB20(cm);
②如图2,展开后连接AB,则AB就是在表面上从A到B的最短距离,
在Rt△ADB中,由勾股定理得:AB(cm);
③如图3,展开后连接AB,则AB就是在表面上A到B的最短距离,
在Rt△ANB中,由勾股定理得:AB7(cm).
∴蚂蚁爬行的最短路程是20cm.
【点评】本题考查了平面展开﹣最短路线问题和勾股定理等知识点,关键是能画出展开图形并能求出符合条件的最短路线.
三.解答题(共5小题)
11.(2024秋 深圳期中)明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词,翻译为:如图秋千细索OA悬挂于O点,静止时竖直下垂,A点为踏板位置,踏板离地高度为1米(AC=1米).将它往前推进一些(EB⊥OC于点E,且EB=4米),踏板升高到点B位置,此时踏板离地2米(BD=CE=2米),求秋千绳(OA或OB)的长度.
【考点】勾股定理的应用.
【专题】等腰三角形与直角三角形;运算能力;应用意识.
【答案】8.5米.
【分析】设OB=OA=x米,则OE=OA﹣AE=(x﹣1)米,在Rt△OBE中,由勾股定理列出方程,解方程即可.
【解答】解:设OB=OA=x米,
∵AE=CE﹣AC=2﹣1=1(米),
∴OE=OA﹣AE=(x﹣1)米,
在Rt△OBE中,由勾股定理得:OB2=EB2+OE2,
即x2=42+(x﹣1)2,
解得:x=8.5,
答:秋千绳(OA或OB)的长度为8.5米.
【点评】本题主要考查了勾股定理的应用,根据勾股定理列出方程是解题的关键.
12.(2024秋 姑苏区校级期中)某校八年(1)班的小华和小轩学习了“勾股定理”之后,为了测得风筝的垂直高度CE,他们进行了如下操作:①测得水平距离BD的长为12米;②根据手中剩余线的长度计算出风筝线BC的长为20米;③牵线放风筝的小明的身高为1.5米.
(1)求风筝的垂直高度CE;
(2)如果小明想风筝沿CD方向再下降4米,则他应该再收回多少米线?
【考点】勾股定理的应用.
【专题】等腰三角形与直角三角形;运算能力;应用意识.
【答案】(1)风筝的高度CE为17.5米;
(2)他应该再收回(20﹣12)米.
【分析】(1)利用勾股定理求出CD的长,再加上DE的长度,即可求出CE的高度;
(2)根据勾股定理即可得到结论.
【解答】解:(1)在Rt△CDB中,
由勾股定理得,CD2=BC2﹣BD2=202﹣122=256,
所以,CD=16(负值舍去),
所以,CE=CD+DE=16+1.5=17.5(米),
答:风筝的高度CE为17.5米;
(2)如图所示:在DC上取一点M,使CM=4米,连接BM,
由题意得,CM=4米,
∴DM=12米,
在Rt△MDB中,
∴BM12(米),
∴BC﹣BM=(20﹣12)米,
∴他应该再收回(20﹣12)米.
【点评】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.
13.(2024秋 昆都仑区校级期中)如图,一架云梯AB斜靠在一竖直的墙AO上,这时AO=20米,云梯AB的长度比OB的长度(云梯底端离墙的距离)大10米,AO⊥BO,设OB的长度为x米.
(1)求OB的长度;
(2)若云梯的顶端A沿墙下滑了5米到达点C处,通过计算说明云梯的底部B往外移动多少米.
【考点】勾股定理的应用.
【专题】等腰三角形与直角三角形;运算能力;推理能力.
【答案】(1)OB的长度为15米;
(2)云梯的底部B往外移动了5米.
【分析】(1)根据勾股定理得出方程求解即可;
(2)由勾股定理求出OD的长即可得出结论.
【解答】解:(1)由题意知,AB=(x+10)米,
在Rt△AOB中,由勾股定理得,
OB2+OA2=AB2,
即x2+202=(x+10)2,
解得x=15,
∴OB的长度为15米;
(2)由题意知,OC=AO﹣AC=20﹣5=15(米),CD=AB=25米,
在Rt△OCD中,由勾股定理得,
OC2+OD2=CD2,
即152+OD2=252,
解得OD=20米(负值舍去),
∴BD=20﹣15=5(米),
∴云梯的底部B往外移动了5米.
【点评】本题考查了勾股定理的应用,熟记勾股定理是解题的关键.
14.(2024秋 江阴市期中)综合实践
徐霞客(1586﹣1641),名弘祖,字振之,号霞客,明朝南直隶江阴(今江苏江阴市)人.明地理学家、旅行家和文学家,地理名著《徐霞客游记》的作者,被称为“千古奇人“.
XX中学数学兴趣小组在徐霞客公园开展综合实践活动.
主题:检测雕塑(如图)底座正面的边AD和边BC是否分别垂直于底边CD.
素材:一个雕塑,一把卷尺
步骤1:利用卷尺测量边AD,底边CD的长度,并测量出点A,C之间的距离;
步骤2:通过计算验证底座正面的边AD和边BC是否分别垂直于底边CD.
解决问题:
通过测量得到边AD的长是60厘米,边CD的长是80厘米,AC的长是100厘米,边AD垂直于边CD吗?为什么?
【考点】勾股定理的应用;有理数的减法.
【专题】三角形;等腰三角形与直角三角形;运算能力.
【答案】垂直,理由见解析.
【分析】根据勾股定理逆定理进行检验即可;
【解答】解:垂直.
理由如下:∵AD=60厘米,CD=80厘米,AC=100厘米,
而602+802=1002,
∴AD2+CD2=AC2,
∴△ACD是直角三角形,
∴AD⊥CD.
【点评】本题考查的是勾股定理的应用,熟记勾股定理是解题的关键.
15.(2024秋 城阳区期中)如图,五一假期,数学兴趣小组的同学来到城阳区澜湾艺术公园露营、放风筝,他们想知道风筝离地面的垂直高度,于是利用所学数学知识来解决实际问题,实践报告如下:
活动课题 探究风筝离地面的垂直高度
活动工具 直角三角板、皮尺等
活动过程 小组成员测量了相关数据,并画出了如图所示的示意图,测得水平距离BC的长为15米,根据手中剩余线的长度计算出风筝线AB的长为17米,牵线放风筝的手到地面的距离为1.5米.(即CD=BE=1.5米)
问题解决 (1)求风筝离地面的垂直高度. (2)如果小明想要把风筝沿射线DA方向再上升12米,且BC长度不变,那么他应该再放出多少米线?
请你帮助兴趣小组解决以上问题.
【考点】勾股定理的应用.
【专题】等腰三角形与直角三角形;运算能力;应用意识.
【答案】(1)风筝离地面的垂直高度为9.5米;
(2)他应该再放出8米长的线.
【分析】(1)在Rt△ABC中,利用勾股定理求出的AC长,即可得到结论;
(2)在Rt△A′BC中,根据勾股定理求出A′B,即可得到结论.
【解答】解:(1)在Rt△ABC中,∠ACB=90°,BC=15米,AB=17米,
由勾股定理得:AC8(米),
∴AD=AC+CD=8+1.5=9.5(米),
答:风筝离地面的垂直高度为9.5米;
(2)如图,当风筝沿DA方向再上升12米时,A'C=12+8=20(米),
在Rt△A′BC中,∠A'CB=90°,BC=15米,
由勾股定理得:A′B25(米),
∴A'B﹣AB=25﹣17=8(米),
答:小明应该再放出8米长的线.
【点评】本题考查了勾股定理的应用,熟练掌握勾股定理,求出AC、A'B的长是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
