2.2代数式的值(预习衔接.夯实基础.含解析)-2025-2026学年七年级上册数学华东师大版(2024)
文档属性
| 名称 | 2.2代数式的值(预习衔接.夯实基础.含解析)-2025-2026学年七年级上册数学华东师大版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 151.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 21:25:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
预习衔接.夯实基础 代数式的值
一.选择题(共5小题)
1.(2024秋 旺苍县期中)如果代数式x﹣2y﹣2的值为2,那么代数式3﹣2x+4y的值是( )
A.﹣2 B.0 C.3 D.﹣5
2.(2024秋 西乡塘区校级期中)当a=﹣2时,代数式﹣3a+5的值是( )
A.11 B.0 C.﹣1 D.﹣11
3.(2024秋 金水区校级期中)若代数式2x2﹣3x的值是6,则代数式1+4x2﹣6x的值是( )
A.﹣12 B.13 C.﹣11 D.11
4.(2024秋 南海区期中)按如图的“数值转换机”计算:若开始输入的x值为3,计算2x+1的值最后输出的结果是( )
A.3 B.7 C.15 D.31
5.(2024秋 龙岗区期中)如图是一个数值转换机,若输入a的值为3,则输出的结果应是( )
A. B. C. D.
二.填空题(共5小题)
6.(2024秋 深圳校级期中)若a,b互为倒数,a,c互为相反数,且d的绝对值为2,则代数式的值为 .
7.(2024秋 同安区期中)若代数式x+2y的值是3,则代数式2x+4y﹣2的值是 .
8.(2024秋 晋江市期中)当x=1时,代数式ax3﹣3bx+2值是﹣4,则当x=﹣1时,代数式ax3﹣3bx﹣5值是 .
9.(2024秋 金牛区校级期中)已知(x+2)(x﹣2)﹣2x=1,则2x2﹣4x+3的值为 .
10.(2024秋 合肥期中)若|a+3|+(b﹣2)2=0,则代数式(a﹣b)2的值为 .
三.解答题(共5小题)
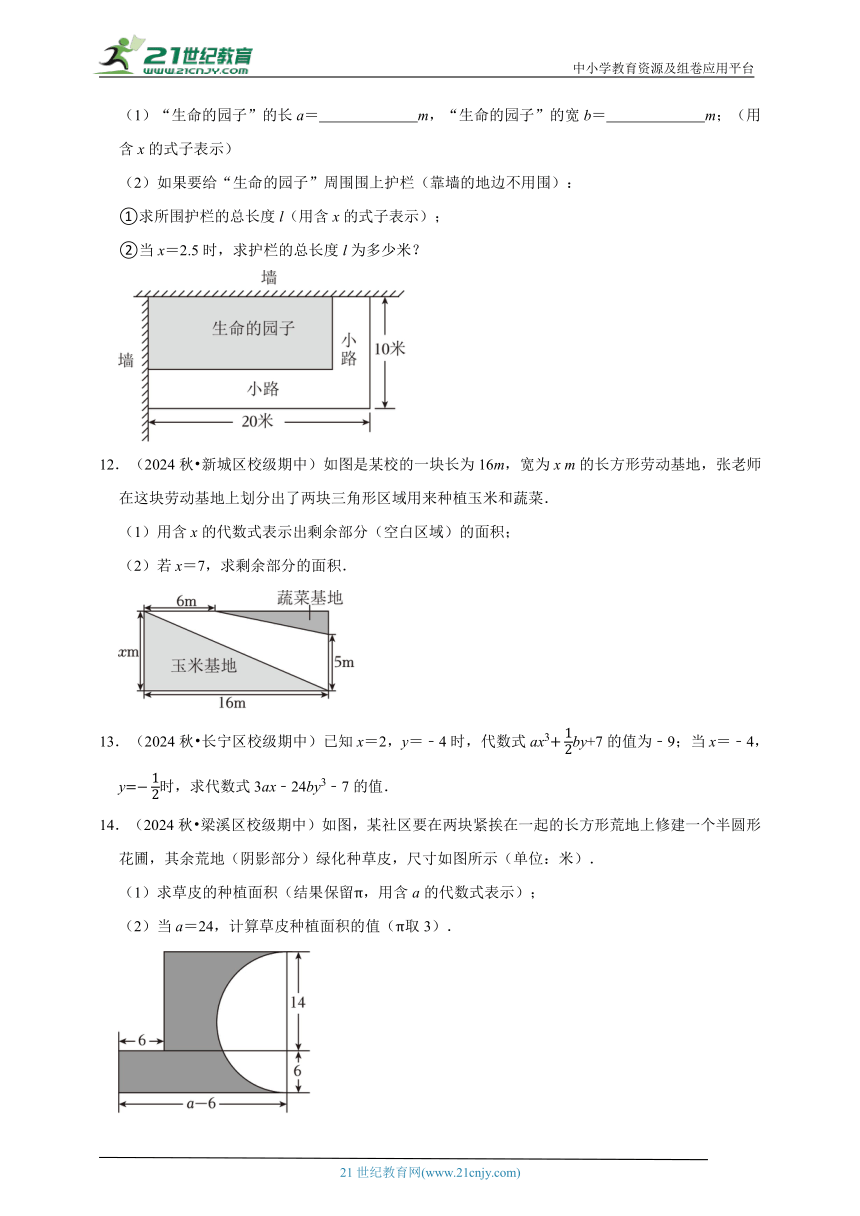
11.(2024秋 天河区校级期中)学校有一块长为20m,宽为10m的长方形空地,现在打算利用这块空地打造一个“生命的园子”(学生自主花园).如图,空地有两面是墙,在不靠墙的两面均需留出宽为x m的小路,余下的长方形部分做为“生命的园子”,种植各种瓜果蔬菜.
(1)“生命的园子”的长a= m,“生命的园子”的宽b= m;(用含x的式子表示)
(2)如果要给“生命的园子”周围围上护栏(靠墙的地边不用围):
①求所围护栏的总长度l(用含x的式子表示);
②当x=2.5时,求护栏的总长度l为多少米?
12.(2024秋 新城区校级期中)如图是某校的一块长为16m,宽为x m的长方形劳动基地,张老师在这块劳动基地上划分出了两块三角形区域用来种植玉米和蔬菜.
(1)用含x的代数式表示出剩余部分(空白区域)的面积;
(2)若x=7,求剩余部分的面积.
13.(2024秋 长宁区校级期中)已知x=2,y=﹣4时,代数式ax3by+7的值为﹣9;当x=﹣4,y时,求代数式3ax﹣24by3﹣7的值.
14.(2024秋 梁溪区校级期中)如图,某社区要在两块紧挨在一起的长方形荒地上修建一个半圆形花圃,其余荒地(阴影部分)绿化种草皮,尺寸如图所示(单位:米).
(1)求草皮的种植面积(结果保留π,用含a的代数式表示);
(2)当a=24,计算草皮种植面积的值(π取3).
15.(2024秋 朝阳区校级期中)【教材呈现】下题是华师版七年级上册数学教材第120页的部分内容.代数式.x2+x+3的值为7,则代数式2x2+2x﹣3的值为 .
【阅读理解】小芳在做作业时采用的方法如下:由题意得x2+x+3=7,则有x2+x=4,
∴2x2+2x﹣3=2(x2+x)﹣3=2×4﹣3=5,
∴代数式:2x2+2x﹣3的值为5.
【方法运用】
(1)若代数式x2+x+1的值为8,则代数式﹣2x2﹣2x+4的值为 .
(2)若当x=2时,ax3+bx+5的值为15,求当x=﹣2时,ax3+bx+3的值.
【拓展应用】
若m2+2mn=﹣2,mn﹣n2=﹣4,则代数式4m2+7mn+n2的值为 .
预习衔接.夯实基础 代数式的值
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 旺苍县期中)如果代数式x﹣2y﹣2的值为2,那么代数式3﹣2x+4y的值是( )
A.﹣2 B.0 C.3 D.﹣5
【考点】代数式求值.
【专题】计算题;整体思想;整式;运算能力.
【答案】D.
【分析】根据已知条件将要求代数式变形,然后整体代入求值即可.
【解答】解:∵3﹣2x+4y=﹣2x+4y+3,
∵x﹣2y﹣2=2,
∴x﹣2y=4,
∴当x﹣2y=4时,原式=﹣2x+4y+3=﹣2(x﹣2y)+3=﹣2×4+3=﹣5.
故选:D.
【点评】本题考查代数式求值,把代数式中的字母用具体的数代替,按照代数式规定的运算,计算的结果就是代数式的值.
2.(2024秋 西乡塘区校级期中)当a=﹣2时,代数式﹣3a+5的值是( )
A.11 B.0 C.﹣1 D.﹣11
【考点】代数式求值.
【专题】计算题;整式;运算能力.
【答案】A.
【分析】利用代入法,代入所求的式子即可.
【解答】解:当a=﹣2时,原式=﹣3×(﹣2)+5=11.
故选:A.
【点评】本题考查代数式求值,把代数式中的字母用具体的数代替,按照代数式规定的运算,计算的结果就是代数式的值.
3.(2024秋 金水区校级期中)若代数式2x2﹣3x的值是6,则代数式1+4x2﹣6x的值是( )
A.﹣12 B.13 C.﹣11 D.11
【考点】代数式求值.
【专题】计算题;整体思想;整式;运算能力.
【答案】B.
【分析】根据已知条件将要求代数式变形,然后整体代入求值即可.
【解答】解:当2x2﹣3x=6时,原式=2(2x2﹣3x)+1=2×6+1=13.
故选:B.
【点评】本题考查代数式求值,把代数式中的字母用具体的数代替,按照代数式规定的运算,计算的结果就是代数式的值.
4.(2024秋 南海区期中)按如图的“数值转换机”计算:若开始输入的x值为3,计算2x+1的值最后输出的结果是( )
A.3 B.7 C.15 D.31
【考点】代数式求值.
【专题】整式;运算能力.
【答案】C
【分析】依据程序图进行运算即可.
【解答】解:开始输入的x值为3,
∵2x+1=2×3+1=7,
将x=7再次输入得:
2×7+1=15,
∴2x+1的值最后输出的结果是15,
故选:C.
【点评】本题主要考查了有理数的混合运算,求代数式的值,本题是操作性题目,理解程序图的实际意义是解题的关键.
5.(2024秋 龙岗区期中)如图是一个数值转换机,若输入a的值为3,则输出的结果应是( )
A. B. C. D.
【考点】代数式求值;有理数的混合运算.
【专题】实数;整式;运算能力.
【答案】B
【分析】根据题意列式计算即可.
【解答】解:若输入a的值为3,
则(32﹣4)
=(9﹣4)
=5
,
故选:B.
【点评】本题考查代数式求值及有理数的混合运算,熟练掌握相关运算法则是解题的关键.
二.填空题(共5小题)
6.(2024秋 深圳校级期中)若a,b互为倒数,a,c互为相反数,且d的绝对值为2,则代数式的值为 或 .
【考点】代数式求值;相反数;绝对值;倒数.
【专题】整式;运算能力.
【答案】或.
【分析】由题意知,ab=1,a+c=0,|d|=2,则d=±2,d2=4,分d=2,d=﹣2,两种情况计算求解即可.
【解答】解:由条件可知:ab=1,a+c=0,|d|=2,d=±2,d2=4,
分类讨论如下:
当d=2时,原式=4﹣2;
当d=﹣2时,原式=4﹣(﹣2);
综上所述,代数式的值为或.
故答案为:或.
【点评】本题考查了倒数,相反数,绝对值,代数式求值.熟练掌握倒数,相反数,绝对值是解题的关键.
7.(2024秋 同安区期中)若代数式x+2y的值是3,则代数式2x+4y﹣2的值是 4 .
【考点】代数式求值.
【专题】计算题;整体思想;整式;运算能力.
【答案】4.
【分析】根据已知条件将要求代数式变形,然后整体代入求值即可.
【解答】解:当x+2y=3时,原式=2(x+2y)﹣2=2×3﹣2=4.
故答案为:4.
【点评】本题考查代数式求值,把代数式中的字母用具体的数代替,按照代数式规定的运算,计算的结果就是代数式的值.
8.(2024秋 晋江市期中)当x=1时,代数式ax3﹣3bx+2值是﹣4,则当x=﹣1时,代数式ax3﹣3bx﹣5值是 1 .
【考点】代数式求值.
【专题】实数;运算能力.
【答案】1.
【分析】把x=1代入ax3﹣3bx+2=﹣4,求出a﹣3b,再把x=﹣1代入ax3﹣3bx﹣5,然后写成含有a﹣3b的形式,最后整体代入求值即可.
【解答】解:∵当x=1时,ax3﹣3bx+2=﹣4,
∴a﹣3b=﹣6,
当x=﹣1时,
ax3﹣3bx﹣5
=(﹣1)3a﹣3b×(﹣1)﹣5
=﹣a+3b﹣5
=﹣(a﹣3b)﹣5
=﹣(﹣6)﹣5
=6﹣5
=1,
故答案为:1.
【点评】本题主要考查考查了代数式求值,解题关键是熟练掌握利用整体代入求值法求代数式的值.
9.(2024秋 金牛区校级期中)已知(x+2)(x﹣2)﹣2x=1,则2x2﹣4x+3的值为 13 .
【考点】代数式求值.
【专题】数与式;运算能力.
【答案】13.
【分析】先利用平方差公式求出x2﹣2x=5,再代入计算即可得.
【解答】解:∵(x+2)(x﹣2)﹣2x=x2﹣4﹣2x=1,
∴x2﹣2x=5,
∴2x2﹣4x+3=2(x2﹣2x)+3=2×5+3=13,
故答案为:13.
【点评】本题考查了平方差公式、代数式求值,熟练掌握整体思想是解题关键.
10.(2024秋 合肥期中)若|a+3|+(b﹣2)2=0,则代数式(a﹣b)2的值为 25 .
【考点】代数式求值;非负数的性质:绝对值;非负数的性质:偶次方.
【专题】计算题;实数;运算能力.
【答案】25.
【分析】根据非负数的性质列出方程求出未知数的值,再代入所求代数式计算即可.
【解答】解:∵|a+3|+(b﹣2)2=0,
∴a+3=0,b﹣2=0,
∴a=﹣3,b=2,
∴(a﹣b)2=(﹣3﹣2)2=25.
故答案为:25.
【点评】本题考查了非负数的性质:掌握几个非负数的和为0,则这几个非负数分别等于0,并正确得出未知数的值是解题的关键.
三.解答题(共5小题)
11.(2024秋 天河区校级期中)学校有一块长为20m,宽为10m的长方形空地,现在打算利用这块空地打造一个“生命的园子”(学生自主花园).如图,空地有两面是墙,在不靠墙的两面均需留出宽为x m的小路,余下的长方形部分做为“生命的园子”,种植各种瓜果蔬菜.
(1)“生命的园子”的长a= (20﹣x) m,“生命的园子”的宽b= (10﹣x) m;(用含x的式子表示)
(2)如果要给“生命的园子”周围围上护栏(靠墙的地边不用围):
①求所围护栏的总长度l(用含x的式子表示);
②当x=2.5时,求护栏的总长度l为多少米?
【考点】代数式求值;列代数式.
【专题】整式;运算能力.
【答案】(1)(20﹣x),(10﹣x);
(2)①30﹣2x;
②25.
【分析】(1)根据长和宽分别减去小路的宽,可得答案;
(2)先根据(1)中的答案,求出“生命的园子”的周长的一半,再代入计算即可.
【解答】解:(1)根据题意,可知a=(20﹣x)m,b=(10﹣x)m,
故答案为:(20﹣x),(10﹣x);
(2)①围护栏的总长度为l=(20﹣x)+(10﹣x)
=20﹣x+10﹣x
=30﹣2x,
答:所围护栏的总长度为(30﹣2x)米;
②当x=2.5时,原式=30﹣2×2.5=30﹣5=25(米),
答:护栏的总长度为25米.
【点评】本题主要考查了求代数式的值,涉及到整式的加减运算,熟练掌握代数式的表示方法,以及整式加减运算法则是解题的关键.
12.(2024秋 新城区校级期中)如图是某校的一块长为16m,宽为x m的长方形劳动基地,张老师在这块劳动基地上划分出了两块三角形区域用来种植玉米和蔬菜.
(1)用含x的代数式表示出剩余部分(空白区域)的面积;
(2)若x=7,求剩余部分的面积.
【考点】代数式求值;列代数式.
【专题】整式;运算能力.
【答案】(1)(3x+25)m2;
(2)46m2.
【分析】(1)空白部分面积等于长方形面积减去玉米基地和蔬菜基地的面积之和,据此列式求解即可;
(2)根据(1)所求,代值计算即可得到答案.
【解答】解:(1)由题意,长方形的面积为:16x(m2),
玉米基地的面积为:16x=8x(m2),蔬菜基地的面积为:(16﹣6)(x﹣5)=5(x﹣5)(m2),
∴空白区域的面积=16x﹣8x﹣5(x﹣5)
=16x﹣8x﹣5x+25
=(3x+25)m2;
(2)将x=7代入3x+25中,得3×7+25=46(m2),
答:剩余部分的面积为46m2.
【点评】本题考查了整式加减的应用,代数式求值,熟练掌握整式的加减运算法则是解题的关键.
13.(2024秋 长宁区校级期中)已知x=2,y=﹣4时,代数式ax3by+7的值为﹣9;当x=﹣4,y时,求代数式3ax﹣24by3﹣7的值.
【考点】代数式求值.
【专题】整式;运算能力.
【答案】17.
【分析】由题意可得8a﹣2b+7=﹣9,即4a﹣b=﹣8,将x=﹣4,y代入3ax﹣24by3﹣7并变形后代入数值计算即可.
【解答】解:∵x=2,y=﹣4时,代数式ax3by+7的值为﹣9,
∴8a﹣2b+7=﹣9,
整理得:4a﹣b=﹣8,
当x=﹣4,y时,
3ax﹣24by3﹣7
=﹣12a+3b﹣7
=﹣3(4a﹣b)﹣7
=﹣3×(﹣8)﹣7
=24﹣7
=17.
【点评】本题考查代数式求值,结合已知条件求得4a﹣b=﹣8是解题的关键.
14.(2024秋 梁溪区校级期中)如图,某社区要在两块紧挨在一起的长方形荒地上修建一个半圆形花圃,其余荒地(阴影部分)绿化种草皮,尺寸如图所示(单位:米).
(1)求草皮的种植面积(结果保留π,用含a的代数式表示);
(2)当a=24,计算草皮种植面积的值(π取3).
【考点】代数式求值;列代数式.
【专题】整式;运算能力.
【答案】(1)S阴影=(20a﹣204﹣50π)平方米;(2)126平方米.
【分析】(1)根据图形表示出正方形ABCD和长方形EFGC的边长,半圆的半径,然后根据“S阴影=S长方形ABCD+S长方形EFGC﹣S半圆”列出代数式即可;
(2)当a=24米,π取3代入(1)的代数式求值即可.
【解答】解:(1)如图所示:
∵四边形ABCD和是四边形EFGC均为长方形,
∴AB=CD,CE=FG=(a﹣6)米,BC=AD=14米,CG=EF=6米,
又∵DE=6,
∴CD=CE﹣DE=a﹣6﹣6=(a﹣12)米,BG=BC+CG=14+6=20米,
∴半圆的半径为10米,
∴S阴影=S长方形ABCD+S长方形EFGC﹣S半圆,
即S阴影=14(a﹣12)+6(a﹣6)π×102=(20a﹣204﹣50π)平方米;
(2)当a=24米,π取3时,
S阴影=20×24﹣204﹣50×3=126(平方米).
【点评】此题主要考查了列代数式,求代数式的值,准确识图,熟练掌握长方形和圆的面积计算公式是解决问题的关键.
15.(2024秋 朝阳区校级期中)【教材呈现】下题是华师版七年级上册数学教材第120页的部分内容.代数式.x2+x+3的值为7,则代数式2x2+2x﹣3的值为 5 .
【阅读理解】小芳在做作业时采用的方法如下:由题意得x2+x+3=7,则有x2+x=4,
∴2x2+2x﹣3=2(x2+x)﹣3=2×4﹣3=5,
∴代数式:2x2+2x﹣3的值为5.
【方法运用】
(1)若代数式x2+x+1的值为8,则代数式﹣2x2﹣2x+4的值为 ﹣10 .
(2)若当x=2时,ax3+bx+5的值为15,求当x=﹣2时,ax3+bx+3的值.
【拓展应用】
若m2+2mn=﹣2,mn﹣n2=﹣4,则代数式4m2+7mn+n2的值为 ﹣4 .
【考点】代数式求值.
【专题】整式;运算能力.
【答案】材料呈现:5;(1)﹣10;(2)﹣7;拓展应用:﹣4.
【分析】(1)利用题干给定的方法,利用整体思想代入求值即可;
(2)利用题干给定的方法,利用整体思想代入求值即可;
拓展应用:根据4(m2+2mn)﹣(mn﹣n2),即可求解.
【解答】解:材料呈现:∵x2+x+3=7,
∴x2+x=4,即2x2+2x=8,
∴2x2+2x﹣3=8﹣3=5,
故答案为:5;
(1)∵x2+x+1=8,
∴x2+x=7,
∴﹣2x2﹣2x+4=﹣2(x2+x)+4=﹣2×7+4=﹣10,
故答案为:﹣10;
(2)∵当x=2时,ax3+bx+5的值为15,
∴23a+2b+5=15,
∴8a+2b=10,
∴当x=﹣2时,
ax3+bx+3,
=(﹣2)3a﹣2b+3,
=﹣8a﹣2b+3,
=﹣(8a+2b)+3,
=﹣10+3,
=﹣7;
拓展应用:∵m2+2mn=﹣2,mn﹣n2=﹣4,mn﹣n2=﹣4,
∴4(m2+2mn)﹣(mn﹣n2)=4×(﹣2)﹣(﹣4),
4m2+8mn﹣mn+n2=﹣4,
4m2+7mn+n2=﹣4,
故答案为:﹣4.
【点评】本题考查了代数式求值,掌握代数式求值的方法是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.夯实基础 代数式的值
一.选择题(共5小题)
1.(2024秋 旺苍县期中)如果代数式x﹣2y﹣2的值为2,那么代数式3﹣2x+4y的值是( )
A.﹣2 B.0 C.3 D.﹣5
2.(2024秋 西乡塘区校级期中)当a=﹣2时,代数式﹣3a+5的值是( )
A.11 B.0 C.﹣1 D.﹣11
3.(2024秋 金水区校级期中)若代数式2x2﹣3x的值是6,则代数式1+4x2﹣6x的值是( )
A.﹣12 B.13 C.﹣11 D.11
4.(2024秋 南海区期中)按如图的“数值转换机”计算:若开始输入的x值为3,计算2x+1的值最后输出的结果是( )
A.3 B.7 C.15 D.31
5.(2024秋 龙岗区期中)如图是一个数值转换机,若输入a的值为3,则输出的结果应是( )
A. B. C. D.
二.填空题(共5小题)
6.(2024秋 深圳校级期中)若a,b互为倒数,a,c互为相反数,且d的绝对值为2,则代数式的值为 .
7.(2024秋 同安区期中)若代数式x+2y的值是3,则代数式2x+4y﹣2的值是 .
8.(2024秋 晋江市期中)当x=1时,代数式ax3﹣3bx+2值是﹣4,则当x=﹣1时,代数式ax3﹣3bx﹣5值是 .
9.(2024秋 金牛区校级期中)已知(x+2)(x﹣2)﹣2x=1,则2x2﹣4x+3的值为 .
10.(2024秋 合肥期中)若|a+3|+(b﹣2)2=0,则代数式(a﹣b)2的值为 .
三.解答题(共5小题)
11.(2024秋 天河区校级期中)学校有一块长为20m,宽为10m的长方形空地,现在打算利用这块空地打造一个“生命的园子”(学生自主花园).如图,空地有两面是墙,在不靠墙的两面均需留出宽为x m的小路,余下的长方形部分做为“生命的园子”,种植各种瓜果蔬菜.
(1)“生命的园子”的长a= m,“生命的园子”的宽b= m;(用含x的式子表示)
(2)如果要给“生命的园子”周围围上护栏(靠墙的地边不用围):
①求所围护栏的总长度l(用含x的式子表示);
②当x=2.5时,求护栏的总长度l为多少米?
12.(2024秋 新城区校级期中)如图是某校的一块长为16m,宽为x m的长方形劳动基地,张老师在这块劳动基地上划分出了两块三角形区域用来种植玉米和蔬菜.
(1)用含x的代数式表示出剩余部分(空白区域)的面积;
(2)若x=7,求剩余部分的面积.
13.(2024秋 长宁区校级期中)已知x=2,y=﹣4时,代数式ax3by+7的值为﹣9;当x=﹣4,y时,求代数式3ax﹣24by3﹣7的值.
14.(2024秋 梁溪区校级期中)如图,某社区要在两块紧挨在一起的长方形荒地上修建一个半圆形花圃,其余荒地(阴影部分)绿化种草皮,尺寸如图所示(单位:米).
(1)求草皮的种植面积(结果保留π,用含a的代数式表示);
(2)当a=24,计算草皮种植面积的值(π取3).
15.(2024秋 朝阳区校级期中)【教材呈现】下题是华师版七年级上册数学教材第120页的部分内容.代数式.x2+x+3的值为7,则代数式2x2+2x﹣3的值为 .
【阅读理解】小芳在做作业时采用的方法如下:由题意得x2+x+3=7,则有x2+x=4,
∴2x2+2x﹣3=2(x2+x)﹣3=2×4﹣3=5,
∴代数式:2x2+2x﹣3的值为5.
【方法运用】
(1)若代数式x2+x+1的值为8,则代数式﹣2x2﹣2x+4的值为 .
(2)若当x=2时,ax3+bx+5的值为15,求当x=﹣2时,ax3+bx+3的值.
【拓展应用】
若m2+2mn=﹣2,mn﹣n2=﹣4,则代数式4m2+7mn+n2的值为 .
预习衔接.夯实基础 代数式的值
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 旺苍县期中)如果代数式x﹣2y﹣2的值为2,那么代数式3﹣2x+4y的值是( )
A.﹣2 B.0 C.3 D.﹣5
【考点】代数式求值.
【专题】计算题;整体思想;整式;运算能力.
【答案】D.
【分析】根据已知条件将要求代数式变形,然后整体代入求值即可.
【解答】解:∵3﹣2x+4y=﹣2x+4y+3,
∵x﹣2y﹣2=2,
∴x﹣2y=4,
∴当x﹣2y=4时,原式=﹣2x+4y+3=﹣2(x﹣2y)+3=﹣2×4+3=﹣5.
故选:D.
【点评】本题考查代数式求值,把代数式中的字母用具体的数代替,按照代数式规定的运算,计算的结果就是代数式的值.
2.(2024秋 西乡塘区校级期中)当a=﹣2时,代数式﹣3a+5的值是( )
A.11 B.0 C.﹣1 D.﹣11
【考点】代数式求值.
【专题】计算题;整式;运算能力.
【答案】A.
【分析】利用代入法,代入所求的式子即可.
【解答】解:当a=﹣2时,原式=﹣3×(﹣2)+5=11.
故选:A.
【点评】本题考查代数式求值,把代数式中的字母用具体的数代替,按照代数式规定的运算,计算的结果就是代数式的值.
3.(2024秋 金水区校级期中)若代数式2x2﹣3x的值是6,则代数式1+4x2﹣6x的值是( )
A.﹣12 B.13 C.﹣11 D.11
【考点】代数式求值.
【专题】计算题;整体思想;整式;运算能力.
【答案】B.
【分析】根据已知条件将要求代数式变形,然后整体代入求值即可.
【解答】解:当2x2﹣3x=6时,原式=2(2x2﹣3x)+1=2×6+1=13.
故选:B.
【点评】本题考查代数式求值,把代数式中的字母用具体的数代替,按照代数式规定的运算,计算的结果就是代数式的值.
4.(2024秋 南海区期中)按如图的“数值转换机”计算:若开始输入的x值为3,计算2x+1的值最后输出的结果是( )
A.3 B.7 C.15 D.31
【考点】代数式求值.
【专题】整式;运算能力.
【答案】C
【分析】依据程序图进行运算即可.
【解答】解:开始输入的x值为3,
∵2x+1=2×3+1=7,
将x=7再次输入得:
2×7+1=15,
∴2x+1的值最后输出的结果是15,
故选:C.
【点评】本题主要考查了有理数的混合运算,求代数式的值,本题是操作性题目,理解程序图的实际意义是解题的关键.
5.(2024秋 龙岗区期中)如图是一个数值转换机,若输入a的值为3,则输出的结果应是( )
A. B. C. D.
【考点】代数式求值;有理数的混合运算.
【专题】实数;整式;运算能力.
【答案】B
【分析】根据题意列式计算即可.
【解答】解:若输入a的值为3,
则(32﹣4)
=(9﹣4)
=5
,
故选:B.
【点评】本题考查代数式求值及有理数的混合运算,熟练掌握相关运算法则是解题的关键.
二.填空题(共5小题)
6.(2024秋 深圳校级期中)若a,b互为倒数,a,c互为相反数,且d的绝对值为2,则代数式的值为 或 .
【考点】代数式求值;相反数;绝对值;倒数.
【专题】整式;运算能力.
【答案】或.
【分析】由题意知,ab=1,a+c=0,|d|=2,则d=±2,d2=4,分d=2,d=﹣2,两种情况计算求解即可.
【解答】解:由条件可知:ab=1,a+c=0,|d|=2,d=±2,d2=4,
分类讨论如下:
当d=2时,原式=4﹣2;
当d=﹣2时,原式=4﹣(﹣2);
综上所述,代数式的值为或.
故答案为:或.
【点评】本题考查了倒数,相反数,绝对值,代数式求值.熟练掌握倒数,相反数,绝对值是解题的关键.
7.(2024秋 同安区期中)若代数式x+2y的值是3,则代数式2x+4y﹣2的值是 4 .
【考点】代数式求值.
【专题】计算题;整体思想;整式;运算能力.
【答案】4.
【分析】根据已知条件将要求代数式变形,然后整体代入求值即可.
【解答】解:当x+2y=3时,原式=2(x+2y)﹣2=2×3﹣2=4.
故答案为:4.
【点评】本题考查代数式求值,把代数式中的字母用具体的数代替,按照代数式规定的运算,计算的结果就是代数式的值.
8.(2024秋 晋江市期中)当x=1时,代数式ax3﹣3bx+2值是﹣4,则当x=﹣1时,代数式ax3﹣3bx﹣5值是 1 .
【考点】代数式求值.
【专题】实数;运算能力.
【答案】1.
【分析】把x=1代入ax3﹣3bx+2=﹣4,求出a﹣3b,再把x=﹣1代入ax3﹣3bx﹣5,然后写成含有a﹣3b的形式,最后整体代入求值即可.
【解答】解:∵当x=1时,ax3﹣3bx+2=﹣4,
∴a﹣3b=﹣6,
当x=﹣1时,
ax3﹣3bx﹣5
=(﹣1)3a﹣3b×(﹣1)﹣5
=﹣a+3b﹣5
=﹣(a﹣3b)﹣5
=﹣(﹣6)﹣5
=6﹣5
=1,
故答案为:1.
【点评】本题主要考查考查了代数式求值,解题关键是熟练掌握利用整体代入求值法求代数式的值.
9.(2024秋 金牛区校级期中)已知(x+2)(x﹣2)﹣2x=1,则2x2﹣4x+3的值为 13 .
【考点】代数式求值.
【专题】数与式;运算能力.
【答案】13.
【分析】先利用平方差公式求出x2﹣2x=5,再代入计算即可得.
【解答】解:∵(x+2)(x﹣2)﹣2x=x2﹣4﹣2x=1,
∴x2﹣2x=5,
∴2x2﹣4x+3=2(x2﹣2x)+3=2×5+3=13,
故答案为:13.
【点评】本题考查了平方差公式、代数式求值,熟练掌握整体思想是解题关键.
10.(2024秋 合肥期中)若|a+3|+(b﹣2)2=0,则代数式(a﹣b)2的值为 25 .
【考点】代数式求值;非负数的性质:绝对值;非负数的性质:偶次方.
【专题】计算题;实数;运算能力.
【答案】25.
【分析】根据非负数的性质列出方程求出未知数的值,再代入所求代数式计算即可.
【解答】解:∵|a+3|+(b﹣2)2=0,
∴a+3=0,b﹣2=0,
∴a=﹣3,b=2,
∴(a﹣b)2=(﹣3﹣2)2=25.
故答案为:25.
【点评】本题考查了非负数的性质:掌握几个非负数的和为0,则这几个非负数分别等于0,并正确得出未知数的值是解题的关键.
三.解答题(共5小题)
11.(2024秋 天河区校级期中)学校有一块长为20m,宽为10m的长方形空地,现在打算利用这块空地打造一个“生命的园子”(学生自主花园).如图,空地有两面是墙,在不靠墙的两面均需留出宽为x m的小路,余下的长方形部分做为“生命的园子”,种植各种瓜果蔬菜.
(1)“生命的园子”的长a= (20﹣x) m,“生命的园子”的宽b= (10﹣x) m;(用含x的式子表示)
(2)如果要给“生命的园子”周围围上护栏(靠墙的地边不用围):
①求所围护栏的总长度l(用含x的式子表示);
②当x=2.5时,求护栏的总长度l为多少米?
【考点】代数式求值;列代数式.
【专题】整式;运算能力.
【答案】(1)(20﹣x),(10﹣x);
(2)①30﹣2x;
②25.
【分析】(1)根据长和宽分别减去小路的宽,可得答案;
(2)先根据(1)中的答案,求出“生命的园子”的周长的一半,再代入计算即可.
【解答】解:(1)根据题意,可知a=(20﹣x)m,b=(10﹣x)m,
故答案为:(20﹣x),(10﹣x);
(2)①围护栏的总长度为l=(20﹣x)+(10﹣x)
=20﹣x+10﹣x
=30﹣2x,
答:所围护栏的总长度为(30﹣2x)米;
②当x=2.5时,原式=30﹣2×2.5=30﹣5=25(米),
答:护栏的总长度为25米.
【点评】本题主要考查了求代数式的值,涉及到整式的加减运算,熟练掌握代数式的表示方法,以及整式加减运算法则是解题的关键.
12.(2024秋 新城区校级期中)如图是某校的一块长为16m,宽为x m的长方形劳动基地,张老师在这块劳动基地上划分出了两块三角形区域用来种植玉米和蔬菜.
(1)用含x的代数式表示出剩余部分(空白区域)的面积;
(2)若x=7,求剩余部分的面积.
【考点】代数式求值;列代数式.
【专题】整式;运算能力.
【答案】(1)(3x+25)m2;
(2)46m2.
【分析】(1)空白部分面积等于长方形面积减去玉米基地和蔬菜基地的面积之和,据此列式求解即可;
(2)根据(1)所求,代值计算即可得到答案.
【解答】解:(1)由题意,长方形的面积为:16x(m2),
玉米基地的面积为:16x=8x(m2),蔬菜基地的面积为:(16﹣6)(x﹣5)=5(x﹣5)(m2),
∴空白区域的面积=16x﹣8x﹣5(x﹣5)
=16x﹣8x﹣5x+25
=(3x+25)m2;
(2)将x=7代入3x+25中,得3×7+25=46(m2),
答:剩余部分的面积为46m2.
【点评】本题考查了整式加减的应用,代数式求值,熟练掌握整式的加减运算法则是解题的关键.
13.(2024秋 长宁区校级期中)已知x=2,y=﹣4时,代数式ax3by+7的值为﹣9;当x=﹣4,y时,求代数式3ax﹣24by3﹣7的值.
【考点】代数式求值.
【专题】整式;运算能力.
【答案】17.
【分析】由题意可得8a﹣2b+7=﹣9,即4a﹣b=﹣8,将x=﹣4,y代入3ax﹣24by3﹣7并变形后代入数值计算即可.
【解答】解:∵x=2,y=﹣4时,代数式ax3by+7的值为﹣9,
∴8a﹣2b+7=﹣9,
整理得:4a﹣b=﹣8,
当x=﹣4,y时,
3ax﹣24by3﹣7
=﹣12a+3b﹣7
=﹣3(4a﹣b)﹣7
=﹣3×(﹣8)﹣7
=24﹣7
=17.
【点评】本题考查代数式求值,结合已知条件求得4a﹣b=﹣8是解题的关键.
14.(2024秋 梁溪区校级期中)如图,某社区要在两块紧挨在一起的长方形荒地上修建一个半圆形花圃,其余荒地(阴影部分)绿化种草皮,尺寸如图所示(单位:米).
(1)求草皮的种植面积(结果保留π,用含a的代数式表示);
(2)当a=24,计算草皮种植面积的值(π取3).
【考点】代数式求值;列代数式.
【专题】整式;运算能力.
【答案】(1)S阴影=(20a﹣204﹣50π)平方米;(2)126平方米.
【分析】(1)根据图形表示出正方形ABCD和长方形EFGC的边长,半圆的半径,然后根据“S阴影=S长方形ABCD+S长方形EFGC﹣S半圆”列出代数式即可;
(2)当a=24米,π取3代入(1)的代数式求值即可.
【解答】解:(1)如图所示:
∵四边形ABCD和是四边形EFGC均为长方形,
∴AB=CD,CE=FG=(a﹣6)米,BC=AD=14米,CG=EF=6米,
又∵DE=6,
∴CD=CE﹣DE=a﹣6﹣6=(a﹣12)米,BG=BC+CG=14+6=20米,
∴半圆的半径为10米,
∴S阴影=S长方形ABCD+S长方形EFGC﹣S半圆,
即S阴影=14(a﹣12)+6(a﹣6)π×102=(20a﹣204﹣50π)平方米;
(2)当a=24米,π取3时,
S阴影=20×24﹣204﹣50×3=126(平方米).
【点评】此题主要考查了列代数式,求代数式的值,准确识图,熟练掌握长方形和圆的面积计算公式是解决问题的关键.
15.(2024秋 朝阳区校级期中)【教材呈现】下题是华师版七年级上册数学教材第120页的部分内容.代数式.x2+x+3的值为7,则代数式2x2+2x﹣3的值为 5 .
【阅读理解】小芳在做作业时采用的方法如下:由题意得x2+x+3=7,则有x2+x=4,
∴2x2+2x﹣3=2(x2+x)﹣3=2×4﹣3=5,
∴代数式:2x2+2x﹣3的值为5.
【方法运用】
(1)若代数式x2+x+1的值为8,则代数式﹣2x2﹣2x+4的值为 ﹣10 .
(2)若当x=2时,ax3+bx+5的值为15,求当x=﹣2时,ax3+bx+3的值.
【拓展应用】
若m2+2mn=﹣2,mn﹣n2=﹣4,则代数式4m2+7mn+n2的值为 ﹣4 .
【考点】代数式求值.
【专题】整式;运算能力.
【答案】材料呈现:5;(1)﹣10;(2)﹣7;拓展应用:﹣4.
【分析】(1)利用题干给定的方法,利用整体思想代入求值即可;
(2)利用题干给定的方法,利用整体思想代入求值即可;
拓展应用:根据4(m2+2mn)﹣(mn﹣n2),即可求解.
【解答】解:材料呈现:∵x2+x+3=7,
∴x2+x=4,即2x2+2x=8,
∴2x2+2x﹣3=8﹣3=5,
故答案为:5;
(1)∵x2+x+1=8,
∴x2+x=7,
∴﹣2x2﹣2x+4=﹣2(x2+x)+4=﹣2×7+4=﹣10,
故答案为:﹣10;
(2)∵当x=2时,ax3+bx+5的值为15,
∴23a+2b+5=15,
∴8a+2b=10,
∴当x=﹣2时,
ax3+bx+3,
=(﹣2)3a﹣2b+3,
=﹣8a﹣2b+3,
=﹣(8a+2b)+3,
=﹣10+3,
=﹣7;
拓展应用:∵m2+2mn=﹣2,mn﹣n2=﹣4,mn﹣n2=﹣4,
∴4(m2+2mn)﹣(mn﹣n2)=4×(﹣2)﹣(﹣4),
4m2+8mn﹣mn+n2=﹣4,
4m2+7mn+n2=﹣4,
故答案为:﹣4.
【点评】本题考查了代数式求值,掌握代数式求值的方法是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
