1.1 积的乘方 课件(共24张PPT) 北师大版(2024)数学七年级下册
文档属性
| 名称 | 1.1 积的乘方 课件(共24张PPT) 北师大版(2024)数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 36.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 18:51:13 | ||
图片预览








文档简介
(共24张PPT)
积的乘方教学课件
2025
年 级:七年级 学 科:数学(北师版)
目 录
积的乘方概念引入
积的乘方公式推导
积的乘方应用实例
积的乘方练习与巩固
积的乘方常见错误分析
积的乘方的拓展学习
01
02
03
04
05
06
积的乘方的实践应用
07
复习提问
1.同底数幂的乘法:
am · an= (m,n 都是正整数)
2.幂的乘方
(am )n= (m,n 都是正整数)
am+n
amn
积的乘方概念引入
Part.
01
新课引入
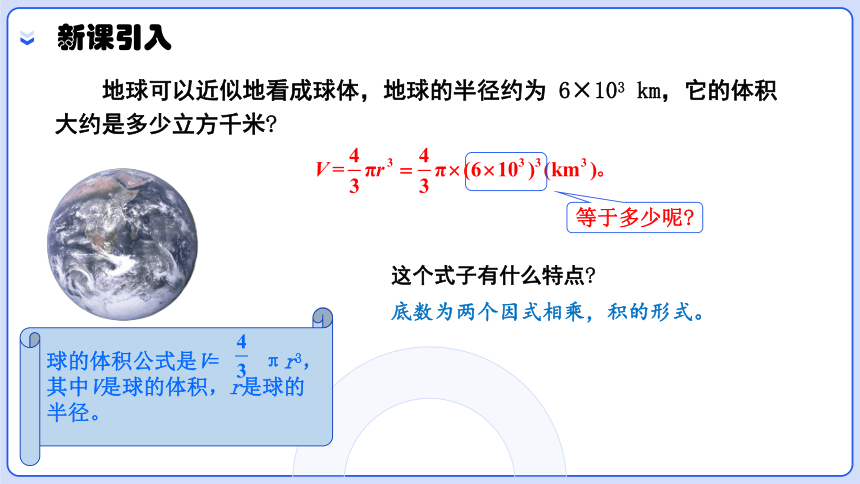
地球可以近似地看成球体,地球的半径约为 6×103 km,它的体积大约是多少立方千米
球的体积公式是V= πr3,其中V是球的体积,r是球的半径。
等于多少呢
这个式子有什么特点
底数为两个因式相乘,积的形式。
思考
(1) (3×5)4 = 3 ( ) · 5 ( );
(2) (3×5)m = 3 ( ) · 5 ( )。
(1) (3×5)4 =(3×5)×(3×5)×(3×5)×(3×5)
= 34×54
4
4
= (3×3×3×3)×(5×5×5×5)
乘方的意义
乘法交换律
乘法结合律
同底数幂的乘法法则
思考
(1) (3×5)4 = 3 ( ) · 5 ( );
(2) (3×5)m = 3 ( ) · 5 ( )。
4
4
= 3m×5m
m
m
(2) (3×5)m = (3×5)×(3×5)×…×(3×5)
m 个 (3×5)
m 个 5
= (3×3×…×3)×(5×5×…×5)
m 个 3
两个数的积的乘方,与这两个数各自的乘方的积相等。
积的乘方公式推导
Part.
02
公式推导
【猜想】 (ab)n=_______(n为正整数)。
anbn
(ab)n = (ab) · (ab) · … · (ab)
= (a · a · … · a)· ( b · b · … · b)
= anbn
n 个 ab
n 个 a
n 个 b
积的乘方等于_______________________。
每个因式分别乘方后的积
公式推导的步骤
积的乘方公式推导主要基于幂运算的基本性质。首先,将多个数相乘的结果表示为一个积,然后对这个积进行幂运算。将积的乘方转化为每个因数分别进行幂运算,再将结果相乘。这一过程不仅验证了积的乘方公式的正确性,也为其应用提供了理论基础。
公式的形式化表达
积的乘方公式可以形式化地表示为:(ab)n = an bn,其中a和b为任意实数,n为正整数。这一公式表明,积的乘方等于各因数分别乘方后的积。通过这一公式,可以将复杂的乘法运算转化为简单的幂运算,从而提高计算效率,减少计算错误。
积的乘方公式的基本形式
积的乘方应用实例
Part.
03
例4 计算:
解:(1) (3x)2 = 32x2 = 9x2;
(2) (– 2b)5 = (– 2)5b5 = – 32b5;
(3) (– 2xy)4 = (– 2)4x4y4 = 16x4y4;
(4) (3a2)n = 3n(a2)n = 3na2n 。
(1) (3x)2; (2) (– 2b) 5;
(3) (– 2xy)4; (4) (3a2)n 。
在实际问题中,积的乘方常用于计算面积和体积。例如,计算长方体的体积时,可以将长、宽、高相乘,再进行幂运算。通过积的乘方公式,可以将这一过程简化为各边长分别乘方后再相乘,从而快速得到结果。这种方法不仅提高了计算效率,也减少了计算错误的可能性。
计算面积和体积
积的乘方在实际问题中的应用
积的乘方在解决增长率问题时也具有重要作用。例如,计算复利时,需要将本金和利率相乘,再进行幂运算。通过积的乘方公式,可以将这一过程转化为本金和利率分别乘方后再相乘,从而快速得到复利结果。这种方法在金融领域具有广泛的应用价值。
解决增长率问题
积的乘方在实际问题中的应用
积的乘方练习与巩固
Part.
04
练一练
1.计算(3m3)2的结果是
2.计算(m3n)2的结果是
3.计算(-4ab2c3)3
积的乘方常见错误分析
Part.
05
混淆积的乘方与幂的乘方
在积的乘方计算中,常常会混淆积的乘方与幂的乘方。积的乘方是指多个数相乘后的结果再进行幂运算,而幂的乘方则是指一个幂再进行幂运算。这两种运算虽然都涉及幂运算,但计算方法和结果截然不同。
积的乘方计算中的常见错误
忽略括号的影响
另一个常见的错误是忽略括号的影响。在积的乘方计算中,括号决定了运算的顺序和范围。如果忽略了括号,可能会导致计算结果错误。例如,计算(2×3)2时,正确的结果应该是36,而如果忽略了括号,直接计算2×32,结果就会变成18。因此,学生需要特别注意括号的作用,确保计算的准确性。
积的乘方计算中的常见错误
积的乘方的拓展学习
Part.
06
拓展
想一想:三个或三个以上的因数的积的乘方等于什么
(abc)n = anbncn(n 是正整数)
幂运算是一种特殊的乘法运算,表示相同因数的连乘。在数学中,幂运算由底数和指数组成,底数是相乘的数,指数是相乘的次数。积的乘方则是指多个数相乘后的结果再进行幂运算,它是幂运算的一种扩展形式,能够简化复杂的乘法运算过程。
幂运算的基本概念
积的乘方指的是将多个数相乘得到的积,再进行幂运算的过程。这一过程可以转化为每个因数分别进行幂运算,然后再将结果相乘。这种转化不仅简化了计算步骤,还使得复杂的乘法运算变得更加直观和易于理解。积的乘方在解决实际问题时具有重要的应用价值。
积的乘方的定义
积的乘方与幂的关系
积的乘方的实践应用
Part.
07
在物理问题中,积的乘方常用于计算力、能量、速度等物理量。例如,计算物体的动能时,需要将质量与速度的平方相乘,再进行幂运算。通过积的乘方公式,可以将这一过程简化为质量和速度分别乘方后再相乘,从而快速得到结果。这种方法在物理计算中具有重要的应用价值。
物理问题中的应用
在化学问题中,积的乘方也发挥着重要作用。例如,计算化学反应的速率时,需要将反应物的浓度相乘,再进行幂运算。通过积的乘方公式,可以将这一过程转化为各反应物浓度分别乘方后再相乘,从而快速得到反应速率。这种方法在化学计算中具有广泛的应用价值。
化学问题中的应用
积的乘方在科学计算中的应用
积的乘方教学课件
2025
年 级:七年级 学 科:数学(北师版)
目 录
积的乘方概念引入
积的乘方公式推导
积的乘方应用实例
积的乘方练习与巩固
积的乘方常见错误分析
积的乘方的拓展学习
01
02
03
04
05
06
积的乘方的实践应用
07
复习提问
1.同底数幂的乘法:
am · an= (m,n 都是正整数)
2.幂的乘方
(am )n= (m,n 都是正整数)
am+n
amn
积的乘方概念引入
Part.
01
新课引入
地球可以近似地看成球体,地球的半径约为 6×103 km,它的体积大约是多少立方千米
球的体积公式是V= πr3,其中V是球的体积,r是球的半径。
等于多少呢
这个式子有什么特点
底数为两个因式相乘,积的形式。
思考
(1) (3×5)4 = 3 ( ) · 5 ( );
(2) (3×5)m = 3 ( ) · 5 ( )。
(1) (3×5)4 =(3×5)×(3×5)×(3×5)×(3×5)
= 34×54
4
4
= (3×3×3×3)×(5×5×5×5)
乘方的意义
乘法交换律
乘法结合律
同底数幂的乘法法则
思考
(1) (3×5)4 = 3 ( ) · 5 ( );
(2) (3×5)m = 3 ( ) · 5 ( )。
4
4
= 3m×5m
m
m
(2) (3×5)m = (3×5)×(3×5)×…×(3×5)
m 个 (3×5)
m 个 5
= (3×3×…×3)×(5×5×…×5)
m 个 3
两个数的积的乘方,与这两个数各自的乘方的积相等。
积的乘方公式推导
Part.
02
公式推导
【猜想】 (ab)n=_______(n为正整数)。
anbn
(ab)n = (ab) · (ab) · … · (ab)
= (a · a · … · a)· ( b · b · … · b)
= anbn
n 个 ab
n 个 a
n 个 b
积的乘方等于_______________________。
每个因式分别乘方后的积
公式推导的步骤
积的乘方公式推导主要基于幂运算的基本性质。首先,将多个数相乘的结果表示为一个积,然后对这个积进行幂运算。将积的乘方转化为每个因数分别进行幂运算,再将结果相乘。这一过程不仅验证了积的乘方公式的正确性,也为其应用提供了理论基础。
公式的形式化表达
积的乘方公式可以形式化地表示为:(ab)n = an bn,其中a和b为任意实数,n为正整数。这一公式表明,积的乘方等于各因数分别乘方后的积。通过这一公式,可以将复杂的乘法运算转化为简单的幂运算,从而提高计算效率,减少计算错误。
积的乘方公式的基本形式
积的乘方应用实例
Part.
03
例4 计算:
解:(1) (3x)2 = 32x2 = 9x2;
(2) (– 2b)5 = (– 2)5b5 = – 32b5;
(3) (– 2xy)4 = (– 2)4x4y4 = 16x4y4;
(4) (3a2)n = 3n(a2)n = 3na2n 。
(1) (3x)2; (2) (– 2b) 5;
(3) (– 2xy)4; (4) (3a2)n 。
在实际问题中,积的乘方常用于计算面积和体积。例如,计算长方体的体积时,可以将长、宽、高相乘,再进行幂运算。通过积的乘方公式,可以将这一过程简化为各边长分别乘方后再相乘,从而快速得到结果。这种方法不仅提高了计算效率,也减少了计算错误的可能性。
计算面积和体积
积的乘方在实际问题中的应用
积的乘方在解决增长率问题时也具有重要作用。例如,计算复利时,需要将本金和利率相乘,再进行幂运算。通过积的乘方公式,可以将这一过程转化为本金和利率分别乘方后再相乘,从而快速得到复利结果。这种方法在金融领域具有广泛的应用价值。
解决增长率问题
积的乘方在实际问题中的应用
积的乘方练习与巩固
Part.
04
练一练
1.计算(3m3)2的结果是
2.计算(m3n)2的结果是
3.计算(-4ab2c3)3
积的乘方常见错误分析
Part.
05
混淆积的乘方与幂的乘方
在积的乘方计算中,常常会混淆积的乘方与幂的乘方。积的乘方是指多个数相乘后的结果再进行幂运算,而幂的乘方则是指一个幂再进行幂运算。这两种运算虽然都涉及幂运算,但计算方法和结果截然不同。
积的乘方计算中的常见错误
忽略括号的影响
另一个常见的错误是忽略括号的影响。在积的乘方计算中,括号决定了运算的顺序和范围。如果忽略了括号,可能会导致计算结果错误。例如,计算(2×3)2时,正确的结果应该是36,而如果忽略了括号,直接计算2×32,结果就会变成18。因此,学生需要特别注意括号的作用,确保计算的准确性。
积的乘方计算中的常见错误
积的乘方的拓展学习
Part.
06
拓展
想一想:三个或三个以上的因数的积的乘方等于什么
(abc)n = anbncn(n 是正整数)
幂运算是一种特殊的乘法运算,表示相同因数的连乘。在数学中,幂运算由底数和指数组成,底数是相乘的数,指数是相乘的次数。积的乘方则是指多个数相乘后的结果再进行幂运算,它是幂运算的一种扩展形式,能够简化复杂的乘法运算过程。
幂运算的基本概念
积的乘方指的是将多个数相乘得到的积,再进行幂运算的过程。这一过程可以转化为每个因数分别进行幂运算,然后再将结果相乘。这种转化不仅简化了计算步骤,还使得复杂的乘法运算变得更加直观和易于理解。积的乘方在解决实际问题时具有重要的应用价值。
积的乘方的定义
积的乘方与幂的关系
积的乘方的实践应用
Part.
07
在物理问题中,积的乘方常用于计算力、能量、速度等物理量。例如,计算物体的动能时,需要将质量与速度的平方相乘,再进行幂运算。通过积的乘方公式,可以将这一过程简化为质量和速度分别乘方后再相乘,从而快速得到结果。这种方法在物理计算中具有重要的应用价值。
物理问题中的应用
在化学问题中,积的乘方也发挥着重要作用。例如,计算化学反应的速率时,需要将反应物的浓度相乘,再进行幂运算。通过积的乘方公式,可以将这一过程转化为各反应物浓度分别乘方后再相乘,从而快速得到反应速率。这种方法在化学计算中具有广泛的应用价值。
化学问题中的应用
积的乘方在科学计算中的应用
同课章节目录
