广东省惠州市博罗县2024-2025学年下学期八年级期末数学试卷(无答案)
文档属性
| 名称 | 广东省惠州市博罗县2024-2025学年下学期八年级期末数学试卷(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 144.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 00:00:00 | ||
图片预览

文档简介
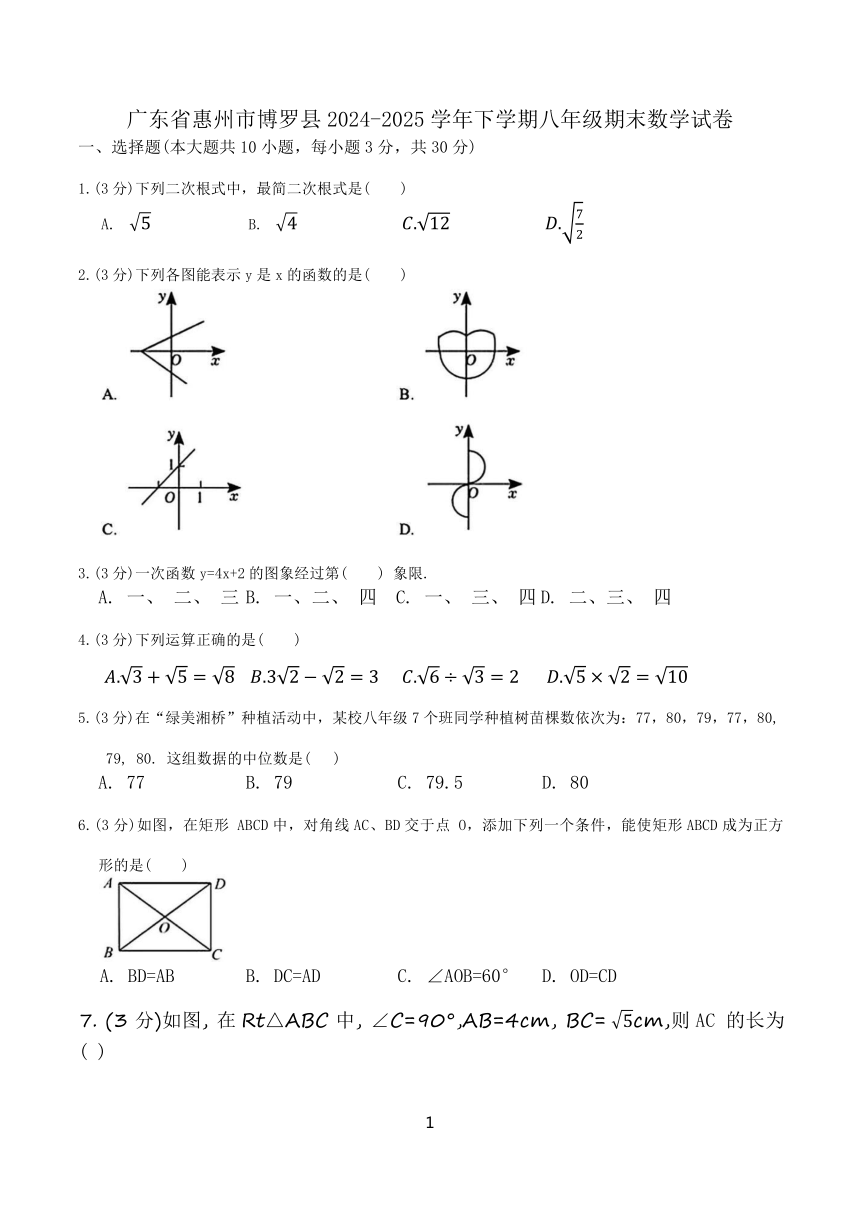
广东省惠州市博罗县2024-2025学年下学期八年级期末数学试卷
一、选择题(本大题共10小题,每小题3分,共30分)
1.(3分)下列二次根式中,最简二次根式是( )
A. B.
2.(3分)下列各图能表示y是x的函数的是( )
3.(3分)一次函数y=4x+2的图象经过第( ) 象限.
A. 一、 二、 三 B. 一、二、 四 C. 一、 三、 四 D. 二、三、 四
4.(3分)下列运算正确的是( )
5.(3分)在“绿美湘桥”种植活动中,某校八年级7个班同学种植树苗棵数依次为:77,80,79,77,80, 79, 80. 这组数据的中位数是( )
A. 77 B. 79 C. 79.5 D. 80
6.(3分)如图,在矩形 ABCD中,对角线AC、BD交于点 O,添加下列一个条件,能使矩形ABCD成为正方形的是( )
A. BD=AB B. DC=AD C. ∠AOB=60° D. OD=CD
7. (3分)如图, 在Rt△ABC中, ∠C=90°,AB=4cm, BC= cm,则AC 的长为( )
A. 3cm D. 1cm
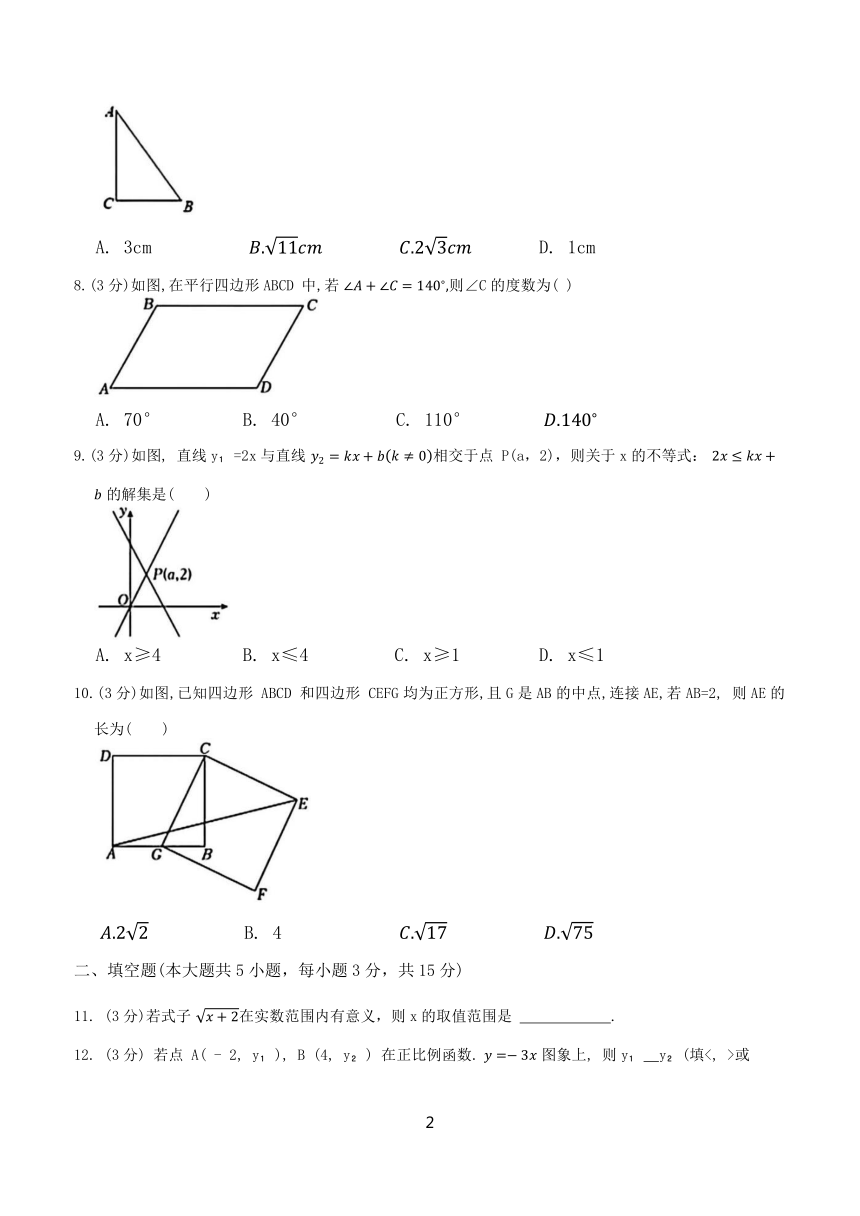
8.(3分)如图,在平行四边形ABCD 中,若 则∠C的度数为( )
A. 70° B. 40° C. 110°
9.(3分)如图, 直线y =2x与直线 相交于点 P(a,2),则关于x的不等式: 的解集是( )
A. x≥4 B. x≤4 C. x≥1 D. x≤1
10.(3分)如图,已知四边形 ABCD 和四边形 CEFG均为正方形,且G是AB的中点,连接AE,若AB=2, 则AE的长为( )
B. 4
二、填空题(本大题共5小题,每小题3分,共15分)
11. (3分)若式子 在实数范围内有意义,则x的取值范围是 .
12. (3分) 若点 A( - 2, y ), B (4, y ) 在正比例函数. 图象上, 则y y (填<, >或
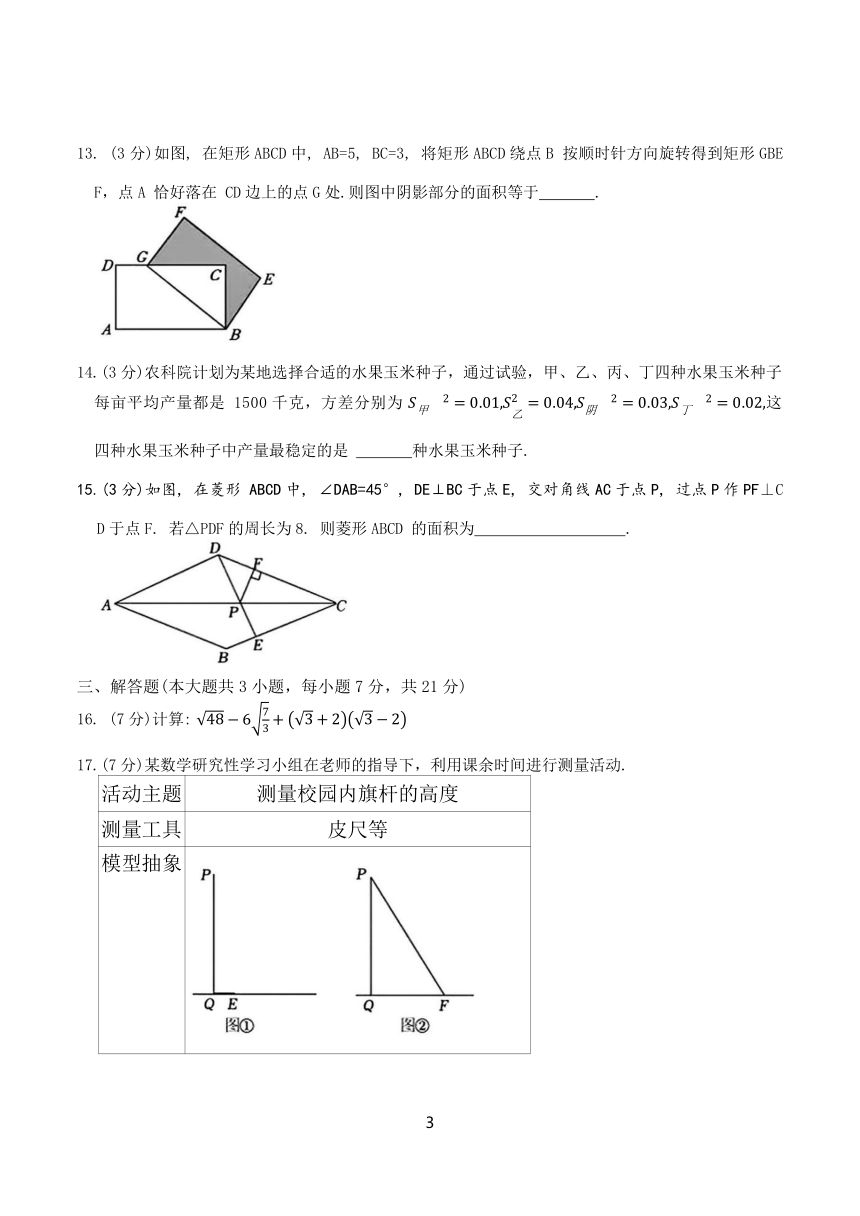
13. (3分)如图, 在矩形ABCD中, AB=5, BC=3, 将矩形ABCD绕点B 按顺时针方向旋转得到矩形GBEF,点A 恰好落在 CD边上的点G处.则图中阴影部分的面积等于 .
14.(3分)农科院计划为某地选择合适的水果玉米种子,通过试验,甲、乙、丙、丁四种水果玉米种子每亩平均产量都是 1500千克,方差分别为 这四种水果玉米种子中产量最稳定的是 种水果玉米种子.
15.(3分)如图, 在菱形 ABCD中, ∠DAB=45°, DE⊥BC于点E, 交对角线AC于点P, 过点P作PF⊥CD于点F. 若△PDF的周长为8. 则菱形ABCD 的面积为 .
三、解答题(本大题共3小题,每小题7分,共21分)
16. (7分)计算:
17.(7分)某数学研究性学习小组在老师的指导下,利用课余时间进行测量活动.
活动主题 测量校园内旗杆的高度
测量工具 皮尺等
模型抽象
注:线段PQ表示旗杆,PQ垂直地面于点Q.
测绘过程 第一次操作:如图①,将系在旗杆顶端的绳子自然下垂到地面,绳子多出的一段在地面拉直后记作QE,用皮尺量出QE的长度;第二次操作:如图②,将绳子拉直,绳子末端落在地面上的点 F处,用皮尺量出QF的长度.
数据信息 图①中QE 的长度为 3m;图②中QF的长度为 9m.
请根据表格中提供的信息,求学校旗杆的高度
18.(7分)已知一次函数的图象经过点 (1,4)和(-2, -5),求这个函数的解析式.
四、解答题(本大题共3小题,每小题9分,共27分)
19.(9分)“防溺水安全”是校园安全教育工作的重点之一,某校为提高学生的安全意识,组织学生举行了一次以“远离溺水·珍爱生命”为主题的防溺水安全知识竞赛,成绩分别为A,B,C,D四个等级,其中相应等级的得分依次记为10分,9分、8分,7分.学校分别从七、八年级各抽取25名学生的竞赛成绩整理并绘制成如下统计图表,请根据提供的信息解答下列问题:
年级 平均分 中位数 众数 方差
七年级 8.76 a 9 1.06
八年级 8.76 8 b 1.38
(1) 根据以上信息可以求出: a= ,b= .
(2)若该校七、八年级各有500人参加本次知识竞赛,且规定9分及以上的成绩为优秀,请估计该校七、八年级参加本次知识竞赛的学生中成绩为优秀的学生共有多少人
20.(9分)为了更好服务我市创建‘国家卫生城市”工作,某商场购进A,B两种新型号的垃圾箱共100个进行销售,两种新型号垃圾箱的进价和售价如表所示,设商场购进A型垃圾箱x个(x为正整数 ),
且所购进的两种型号垃圾箱能全部卖出,获得的总利润为 w元.
(1)求总利润w关于x的函数关系式
(2)如果购进两种垃圾箱的总费用不超过6000元,那么该商场如何进货才能获利最多 并求出最大利润.
A 型垃圾箱 B型垃圾箱
进价(元/个) 62 54
售价(元/个) 76 60
21. (9分)如图, 已知在△ABC中, ∠BAC=90°, D是BC的中点, E是AD的中点, 过点A作AF∥BC交 BE的延长线于点 F,连接 CF.
(1) 求证: 四边形 ADCF是菱形;
(2)若AC=8, 菱形 ADCF的面积为40, 求AB的长
五、解答题(本大题共2小题,22小题13分,23小题14分,共27分)
22. (13分)综合与实践
正方形 ABCD中,AC为对角线,点P 在线段AC上运动,以PD 为边作正方形DPFE,连接CE;
【初步探究】
(1)如图1,当点P在线段 AC上时,AP与CE 的数量关系是 ;AP与 CE的位置关系为 ; CD, PC, CE三者的数量关系为 ;
【探索发现】
(2)当点P 在线段 AC延长线上运动时,如图2,探究线段CD,PC和CE 三者之间数量关系,并说明理由;
【拓展延伸】
(3)如图3, 连接AE, 若 则CP 的长为 .
23. (14分) 如图1, 直线 与x轴,y轴分别交于点A,B,直线 与直线AB交于点C,与y轴交于点 D.
(1)求点 C的坐标.
(2)求 的面积
(3)如图2,P是y轴正半轴上的一点,Q 是直线AB上的一点,连接PQ.
①若 轴,且点 A 关于直线PQ 的对称点. 恰好落在直线CD上,求PQ的长②若BDC与 全等(点Q不与点 C重合),请写出所有满足要求的点Q坐标 (直接写出答案)
一、选择题(本大题共10小题,每小题3分,共30分)
1.(3分)下列二次根式中,最简二次根式是( )
A. B.
2.(3分)下列各图能表示y是x的函数的是( )
3.(3分)一次函数y=4x+2的图象经过第( ) 象限.
A. 一、 二、 三 B. 一、二、 四 C. 一、 三、 四 D. 二、三、 四
4.(3分)下列运算正确的是( )
5.(3分)在“绿美湘桥”种植活动中,某校八年级7个班同学种植树苗棵数依次为:77,80,79,77,80, 79, 80. 这组数据的中位数是( )
A. 77 B. 79 C. 79.5 D. 80
6.(3分)如图,在矩形 ABCD中,对角线AC、BD交于点 O,添加下列一个条件,能使矩形ABCD成为正方形的是( )
A. BD=AB B. DC=AD C. ∠AOB=60° D. OD=CD
7. (3分)如图, 在Rt△ABC中, ∠C=90°,AB=4cm, BC= cm,则AC 的长为( )
A. 3cm D. 1cm
8.(3分)如图,在平行四边形ABCD 中,若 则∠C的度数为( )
A. 70° B. 40° C. 110°
9.(3分)如图, 直线y =2x与直线 相交于点 P(a,2),则关于x的不等式: 的解集是( )
A. x≥4 B. x≤4 C. x≥1 D. x≤1
10.(3分)如图,已知四边形 ABCD 和四边形 CEFG均为正方形,且G是AB的中点,连接AE,若AB=2, 则AE的长为( )
B. 4
二、填空题(本大题共5小题,每小题3分,共15分)
11. (3分)若式子 在实数范围内有意义,则x的取值范围是 .
12. (3分) 若点 A( - 2, y ), B (4, y ) 在正比例函数. 图象上, 则y y (填<, >或
13. (3分)如图, 在矩形ABCD中, AB=5, BC=3, 将矩形ABCD绕点B 按顺时针方向旋转得到矩形GBEF,点A 恰好落在 CD边上的点G处.则图中阴影部分的面积等于 .
14.(3分)农科院计划为某地选择合适的水果玉米种子,通过试验,甲、乙、丙、丁四种水果玉米种子每亩平均产量都是 1500千克,方差分别为 这四种水果玉米种子中产量最稳定的是 种水果玉米种子.
15.(3分)如图, 在菱形 ABCD中, ∠DAB=45°, DE⊥BC于点E, 交对角线AC于点P, 过点P作PF⊥CD于点F. 若△PDF的周长为8. 则菱形ABCD 的面积为 .
三、解答题(本大题共3小题,每小题7分,共21分)
16. (7分)计算:
17.(7分)某数学研究性学习小组在老师的指导下,利用课余时间进行测量活动.
活动主题 测量校园内旗杆的高度
测量工具 皮尺等
模型抽象
注:线段PQ表示旗杆,PQ垂直地面于点Q.
测绘过程 第一次操作:如图①,将系在旗杆顶端的绳子自然下垂到地面,绳子多出的一段在地面拉直后记作QE,用皮尺量出QE的长度;第二次操作:如图②,将绳子拉直,绳子末端落在地面上的点 F处,用皮尺量出QF的长度.
数据信息 图①中QE 的长度为 3m;图②中QF的长度为 9m.
请根据表格中提供的信息,求学校旗杆的高度
18.(7分)已知一次函数的图象经过点 (1,4)和(-2, -5),求这个函数的解析式.
四、解答题(本大题共3小题,每小题9分,共27分)
19.(9分)“防溺水安全”是校园安全教育工作的重点之一,某校为提高学生的安全意识,组织学生举行了一次以“远离溺水·珍爱生命”为主题的防溺水安全知识竞赛,成绩分别为A,B,C,D四个等级,其中相应等级的得分依次记为10分,9分、8分,7分.学校分别从七、八年级各抽取25名学生的竞赛成绩整理并绘制成如下统计图表,请根据提供的信息解答下列问题:
年级 平均分 中位数 众数 方差
七年级 8.76 a 9 1.06
八年级 8.76 8 b 1.38
(1) 根据以上信息可以求出: a= ,b= .
(2)若该校七、八年级各有500人参加本次知识竞赛,且规定9分及以上的成绩为优秀,请估计该校七、八年级参加本次知识竞赛的学生中成绩为优秀的学生共有多少人
20.(9分)为了更好服务我市创建‘国家卫生城市”工作,某商场购进A,B两种新型号的垃圾箱共100个进行销售,两种新型号垃圾箱的进价和售价如表所示,设商场购进A型垃圾箱x个(x为正整数 ),
且所购进的两种型号垃圾箱能全部卖出,获得的总利润为 w元.
(1)求总利润w关于x的函数关系式
(2)如果购进两种垃圾箱的总费用不超过6000元,那么该商场如何进货才能获利最多 并求出最大利润.
A 型垃圾箱 B型垃圾箱
进价(元/个) 62 54
售价(元/个) 76 60
21. (9分)如图, 已知在△ABC中, ∠BAC=90°, D是BC的中点, E是AD的中点, 过点A作AF∥BC交 BE的延长线于点 F,连接 CF.
(1) 求证: 四边形 ADCF是菱形;
(2)若AC=8, 菱形 ADCF的面积为40, 求AB的长
五、解答题(本大题共2小题,22小题13分,23小题14分,共27分)
22. (13分)综合与实践
正方形 ABCD中,AC为对角线,点P 在线段AC上运动,以PD 为边作正方形DPFE,连接CE;
【初步探究】
(1)如图1,当点P在线段 AC上时,AP与CE 的数量关系是 ;AP与 CE的位置关系为 ; CD, PC, CE三者的数量关系为 ;
【探索发现】
(2)当点P 在线段 AC延长线上运动时,如图2,探究线段CD,PC和CE 三者之间数量关系,并说明理由;
【拓展延伸】
(3)如图3, 连接AE, 若 则CP 的长为 .
23. (14分) 如图1, 直线 与x轴,y轴分别交于点A,B,直线 与直线AB交于点C,与y轴交于点 D.
(1)求点 C的坐标.
(2)求 的面积
(3)如图2,P是y轴正半轴上的一点,Q 是直线AB上的一点,连接PQ.
①若 轴,且点 A 关于直线PQ 的对称点. 恰好落在直线CD上,求PQ的长②若BDC与 全等(点Q不与点 C重合),请写出所有满足要求的点Q坐标 (直接写出答案)
同课章节目录
