冀教版(2024)七年级数学下册 6.2 二元一次方程组的解法 课件(共17张PPT)
文档属性
| 名称 | 冀教版(2024)七年级数学下册 6.2 二元一次方程组的解法 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 07:37:02 | ||
图片预览





文档简介
(共17张PPT)
6.2 二元一次方程组的解法
陌
1、理解加减消元法的含义.
2、会用加减法解二元一次方程组.
3、初步体会解二元一次方程组的基本思想——
“消元”.
学习目标
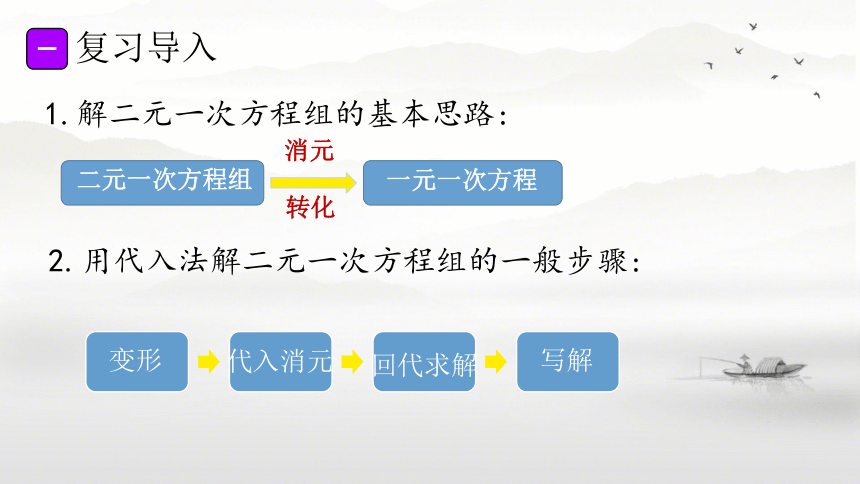
一
复习导入
1.解二元一次方程组的基本思路:
二元一次方程组
消元
转化
一元一次方程
2.用代入法解二元一次方程组的一般步骤:
变形
代入消元
回代求解
写解
5x+3y=16 ①
2x-3y=-2 ②
{
解:①+②,得
7x=14,
x=2.
把x=2代入①,得
10+3y=16,
y=2.
∴原方程组的解为
{
x=2
y=2.
例4
解方程组
解方程组
解:①-②,得
3y=6,
y=2.
把y=2代入②,得
3x-2=1,
x=1.
∴原方程组的解为
观察比较:
1.可以用②-①吗?
2.①-②与②-①相比,哪个较好呢?
注意:两式相减应以未知数的系数得正数为宜。
②
①
做一做
将二元一次方程组中两个方程相加 (或相减 ,或进行适当变形后再加减 ),消去一个未知数 ,得到一元一次方程 ,通过求解一元一次方程,再求得二元一次方程组的解 ,这种解方程组的方法叫做加减消元法 ,简称 加减法。
应用这种解法解方程组
的前提条件是什么?
两个二元一次方程中同一
个未知数的系数相反或相等.
什么条件下用加法、
什么条件下用减法?
某个未知数的系数互为相反数
时用加法,系数相等时用减法.
小结
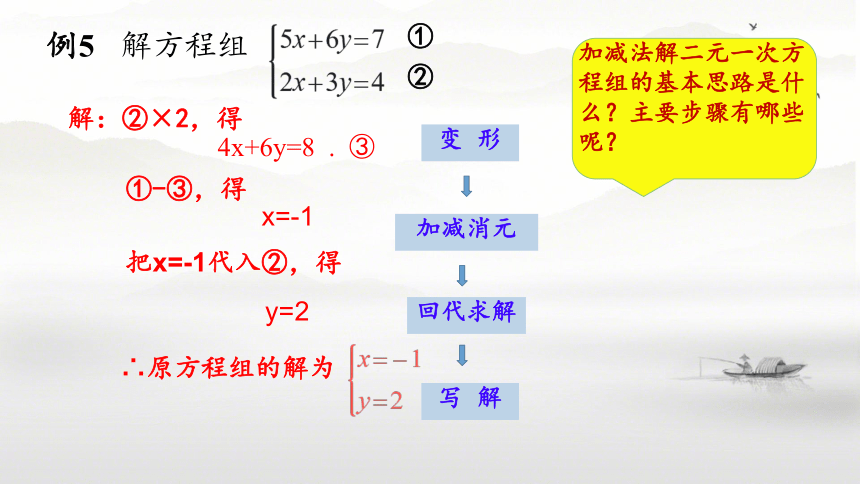
例5
解方程组
①
②
解:②×2,得
4x+6y=8 . ③
①-③,得
x=-1
把x=-1代入②,得
y=2
∴原方程组的解为
加减法解二元一次方程组的基本思路是什么?主要步骤有哪些呢?
变 形
加减消元
回代求解
写 解
二元一次
方程组
一元一次
方程
一元一次
方程的解
得解
加减消元
7x=14
求
解
x= 2
代入
5 × 2+3y=16
求
解
y= 2
得解
小结
课本13页 练习 第1题、第2题
课本13页 A组 第1题(1)(2)
对应练习
1.已知方程组
则x+y的值为( ).
A.-1 B.0 C.2 D.3
2.已知方程组
与
有相同的解,
求m、n的值.
当堂练习
A
课堂总结
课后作业
解
6.2 二元一次方程组的解法
陌
1、理解加减消元法的含义.
2、会用加减法解二元一次方程组.
3、初步体会解二元一次方程组的基本思想——
“消元”.
学习目标
一
复习导入
1.解二元一次方程组的基本思路:
二元一次方程组
消元
转化
一元一次方程
2.用代入法解二元一次方程组的一般步骤:
变形
代入消元
回代求解
写解
5x+3y=16 ①
2x-3y=-2 ②
{
解:①+②,得
7x=14,
x=2.
把x=2代入①,得
10+3y=16,
y=2.
∴原方程组的解为
{
x=2
y=2.
例4
解方程组
解方程组
解:①-②,得
3y=6,
y=2.
把y=2代入②,得
3x-2=1,
x=1.
∴原方程组的解为
观察比较:
1.可以用②-①吗?
2.①-②与②-①相比,哪个较好呢?
注意:两式相减应以未知数的系数得正数为宜。
②
①
做一做
将二元一次方程组中两个方程相加 (或相减 ,或进行适当变形后再加减 ),消去一个未知数 ,得到一元一次方程 ,通过求解一元一次方程,再求得二元一次方程组的解 ,这种解方程组的方法叫做加减消元法 ,简称 加减法。
应用这种解法解方程组
的前提条件是什么?
两个二元一次方程中同一
个未知数的系数相反或相等.
什么条件下用加法、
什么条件下用减法?
某个未知数的系数互为相反数
时用加法,系数相等时用减法.
小结
例5
解方程组
①
②
解:②×2,得
4x+6y=8 . ③
①-③,得
x=-1
把x=-1代入②,得
y=2
∴原方程组的解为
加减法解二元一次方程组的基本思路是什么?主要步骤有哪些呢?
变 形
加减消元
回代求解
写 解
二元一次
方程组
一元一次
方程
一元一次
方程的解
得解
加减消元
7x=14
求
解
x= 2
代入
5 × 2+3y=16
求
解
y= 2
得解
小结
课本13页 练习 第1题、第2题
课本13页 A组 第1题(1)(2)
对应练习
1.已知方程组
则x+y的值为( ).
A.-1 B.0 C.2 D.3
2.已知方程组
与
有相同的解,
求m、n的值.
当堂练习
A
课堂总结
课后作业
解
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
