冀教版(2024)七年级数学下册 10.2三角形的外角及其性质 课件(共25张PPT)
文档属性
| 名称 | 冀教版(2024)七年级数学下册 10.2三角形的外角及其性质 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 601.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 00:00:00 | ||
图片预览



文档简介
(共25张PPT)
第十章 三角形
三角形的外角及其性质
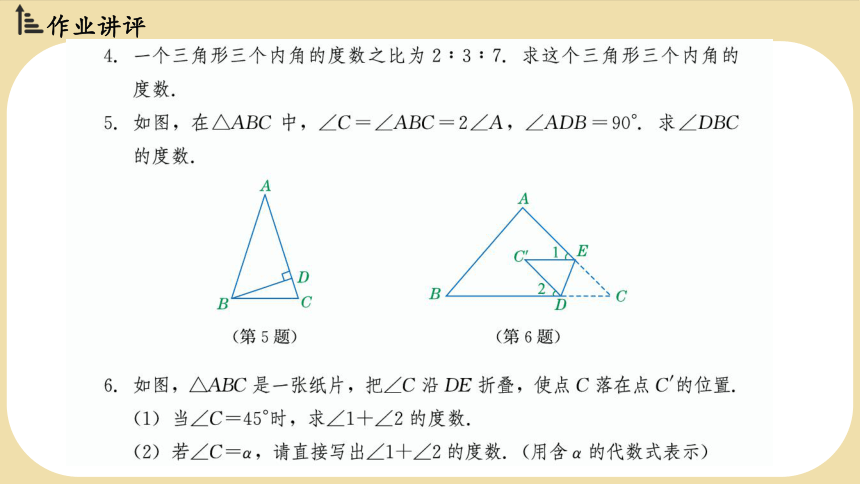
作业讲评
知识回顾
1.什么是三角形的内角?其和等于多少?
三角形相邻两边组成的角叫做三角形的内角,它们的和是180 °
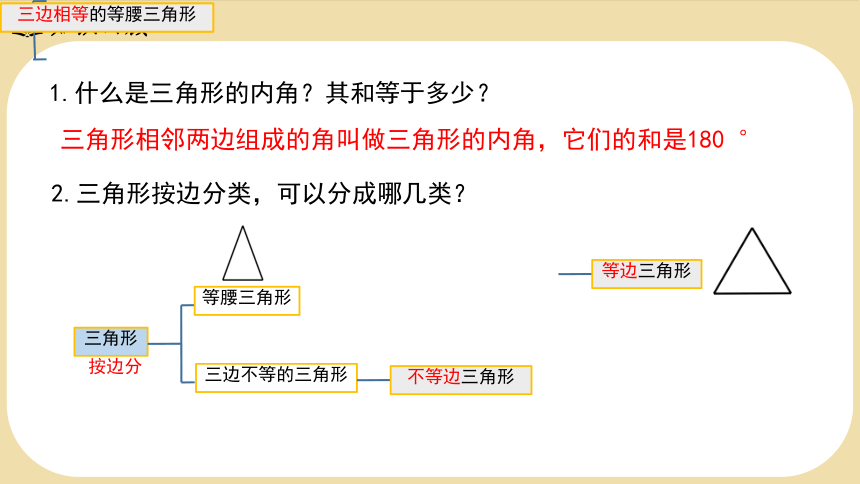
2.三角形按边分类,可以分成哪几类?
两边相等的等腰三角形
三边相等的等腰三角形
等边三角形
三角形
等腰三角形
三边不等的三角形
按边分
不等边三角形
课堂导入
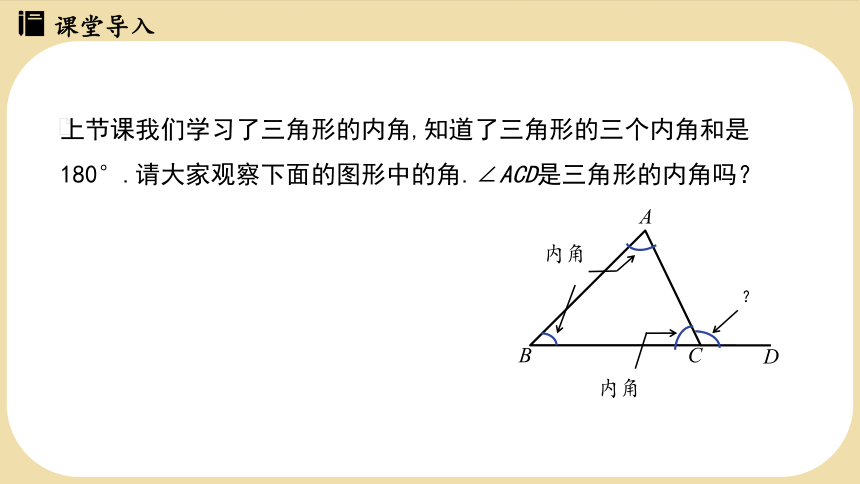
上节课我们学习了三角形的内角,知道了三角形的三个内角和是180°.请大家观察下面的图形中的角.∠ACD是三角形的内角吗?
A
D
C
B
?
内角
内角
新知探究
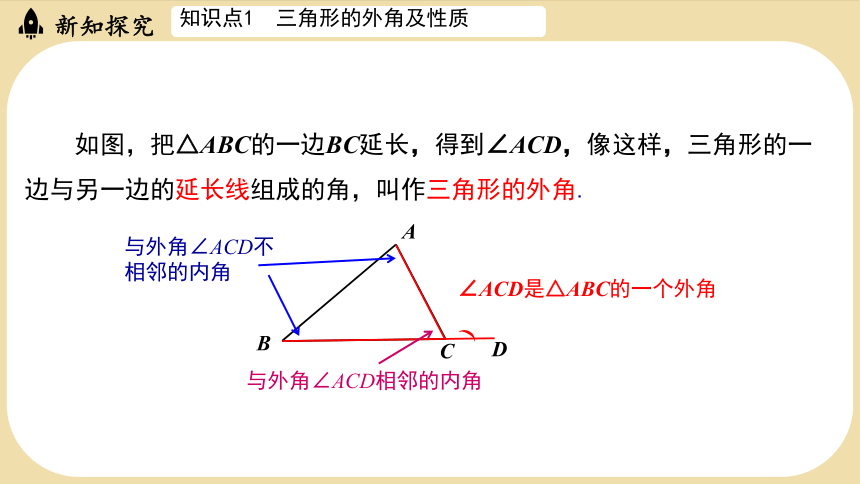
如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫作三角形的外角.
A
B
C
D
(
∠ACD是△ABC的一个外角
与外角∠ACD不相邻的内角
与外角∠ACD相邻的内角
知识点1 三角形的外角及性质
新知探究
(
(
(
(
(
(
A
B
C
1
2
3
4
5
6
A
B
C
问题1:△ABC如图所示,请画出△ABC的所有外角,指出来有哪几个.
有6个,它们是∠1, ∠2, ∠3, ∠4, ∠5, ∠6.
问题2:△ABC的6个外角有什么关系
∠1和∠4, 是对顶角,相等;
∠2和∠5, 是对顶角,相等;
∠3和∠6, 是对顶角,相等.
知识点1 三角形的外角及性质
新知探究
问题3:在图中,外角∠ACD与它不相邻的内角∠A,∠B之间有什么大小关系?
解:∵∠ACD+∠ACB = 180°,(补角的定义)
∠A +∠B +∠ACB = 180°,(三角形的内角和定理)
∴∠ACD-∠A-∠B = 0.
∴∠ACD =∠A +∠B.
∵∠A>0,∠B>0,
∴∠ACD>∠A,∠ACD>∠B.
知识点1 三角形的外角及性质
新知探究
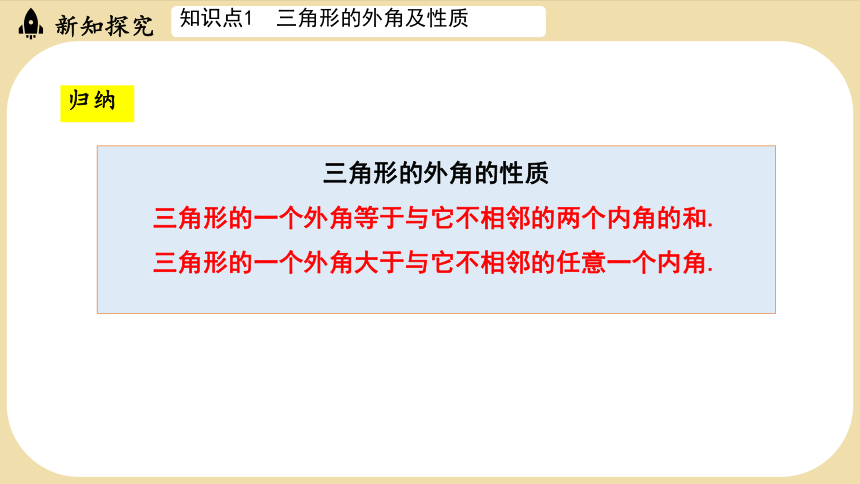
三角形的外角的性质
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于与它不相邻的任意一个内角.
归纳
知识点1 三角形的外角及性质
新知探究
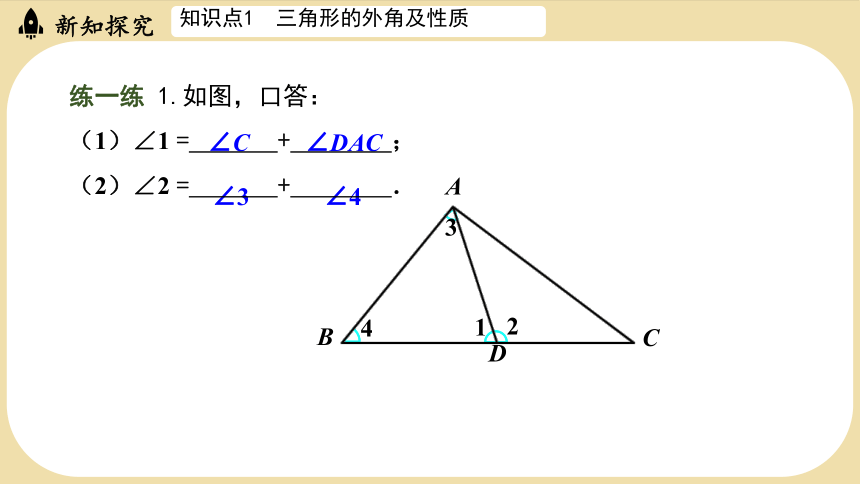
∠C
∠3
∠DAC
∠4
练一练 1.如图,口答:
(1)∠1 = + ;
(2)∠2 = + .
B
A
C
D
1
2
3
4
知识点1 三角形的外角及性质
新知探究
练一练 2.如图,说出图形中∠1 的度数.
(1) (2)
(3) (4)
30°
60°
1
35°
60°
1
45°
50°
1
30°
15°
1
知识点1 三角形的外角及性质
新知探究
例1 如图,∠BCD=92°,∠A=27°,∠BED=44°,求:
(1) ∠B的度数;(2) ∠BFD的度数;
A
C
D
E
B
解:(1) 在△ABC中,∵ ∠BCD=∠A+∠B(三角形的一个外角等于与它不相邻的两个内角的和),
∠BCD=92°,∠A=27°,(已知)
∴∠B=∠BCD-∠A=92°-27°=65°;
(2) 在△BEF中,∵ ∠BFD=∠B+∠BED(三角形的一个外角等于与它不相邻的两个内角的和),
∠BED=44°,∠B=65°,(已知)
∴∠BFD=44°+65°=109°.
知识点1 三角形的外角及性质
F
新知探究
练一练 如图,∠BAE,∠CBF,∠ACD 是△ABC 的三个外角,它们的和是多少?
解法一:
∵ ∠BAE =∠2 +∠3,
∠CBF =∠1 +∠3,
∠ACD =∠1 +∠2,
∴ ∠BAE +∠CBF +∠ACD
= (∠2 +∠3)+(∠1 +∠3)+ (∠1 +∠2)
A
B
F
C
D
E
1
2
3
= 2(∠1 +∠2 +∠3).
∵ ∠1 +∠2 +∠3 =180°,
∴ ∠BAE +∠CBF +∠ACD = 2×180°=360°.
知识点1 三角形的外角及性质
新知探究
A
B
F
C
D
E
1
2
3
由∠1 + ∠2 + ∠3 =180°,
得∠BAE + ∠CBF + ∠ACD
= 540°- 180°
=360°.
解法二:
由∠1 +∠BAE =180°,
∠2 +∠CBF =180°,
∠3 +∠ACD =180°,
得∠1 +∠2 +∠3 + ∠BAE+∠CBF +∠ACD = 540°.
归纳:三角形的外角和360°.
知识点1 三角形的外角及性质
新知探究
谈一谈
1.一个三角形的内角最多有几个直角,最多有几个钝角?
2.一个三角形能不能三个内角都是锐角?
知识点2 三角形按角分类
新知探究
问题4:按照三角形内角的大小,三角形可以分为哪几类?
锐角三角形
直角三角形
钝角三角形.
三个内角都是锐角的三角形
有一个内角是直角的三角形
有一个内角是钝角的三角形
知识点2 三角形按角分类
新知探究
请你试着以角为标准对三角形进行分类
两边相等的等腰三角形
三边相等的等腰三角形
三角形
按角分
锐角三角形
直角三角形
钝角三角形
等腰直角三角形
等边三角形
三角形
等腰三角形
三边不等的三角形
按边分
不等边三角形
知识点2 三角形按角分类
随堂练习
1.如果三角形三个外角度数之比是3:4:5,则此三角形一定是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
2.已知,如图,△ABC 中,∠B=∠DAC,则∠BAC 和∠ADC的关系是( )
A.∠BAC<∠ADC B.∠BAC=∠ADC
C.∠BAC>∠ADC D.不能确定
B
B
3.如图,AB//CD,∠A=37°, ∠C=63°,那么∠F
等于( )
F
A
B
E
C
D
A.26°
B.63°
C.37°
D.60°
A
A
B
C
D
E
1
2
F
G
解:∵∠1是△FBE的外角,
∴∠1=∠B+ ∠E,
同理∠2=∠A+∠D.
在△CFG中 ,
∠C+∠1+∠2=180 ,
∴∠A+ ∠ B+∠C+ ∠ D+∠E= 180 .
4.如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
拓展提升
下面给出的四个三角形都有一部分被遮挡,其中不能判断三角形类型的是( )
C
1
2
一个零件的形状如图所示,按规定∠A 应等于90°,
∠B 和∠C 分别是21°和20°,质量检验员量得∠BDC=
130°后就断定这个零件不合格.请说明为什么?
如图,在△ABC 中,D 为BC 的延长线上一点,∠A=60°,
∠ABC 和∠ACD 的平分线交于点O,求∠O 的度数.
由题意得∠OBC= ∠ABC,
∠DCO= ∠ACD,
∴∠O=∠DCO-∠OBC= ∠ACD- ∠ABC=
(∠ACD-∠ABC )= ∠A=30°.
解:
3
如图,连接AD 并延长到点E,
则∠CDE=∠C+∠2,
∠BDE=∠B+∠1.
所以∠CDE+∠BDE=∠C+∠2+∠B+∠1.
即∠BDC=∠C+∠B+∠CAB.
若零件合格,则∠BDC=20°+21°+90°=131°.
而量得∠BDC=130°,所以这个零件不合格.
解:
归纳小结
三角形的外角
三角形外角的性质
三角形的分类
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于与它不相邻的任意一个内角.
按边分类
按角分类
等腰三角形
不等边三角形
锐角三角形
直角三角形
钝角三角形
新知探究
例2 (一题多解)如图,计算∠BDC.
A
B
C
D
(
(
(
51 °
20 °
30 °
解:(解法一)连接AD并延长于点E.
在△ABD中,∠1+∠ABD=∠3,
在△ACD中,∠2+∠ACD=∠4.
因为∠BDC=∠3+∠4,∠BAC=∠1+∠2,
所以∠BDC=∠BAC+∠ABD+∠ACD
=51° +20°+30°=101°.
(解法二)延长BD交AC于点E.
在△ABE中,∠1=∠ABE+∠BAE,
在△ECD中,∠BDC=∠1+∠ECD.
所以∠BDC=∠BAC+∠ABD+∠ACD
=51° +20°+30°=101°.
知识点1 三角形的外角及性质
第十章 三角形
三角形的外角及其性质
作业讲评
知识回顾
1.什么是三角形的内角?其和等于多少?
三角形相邻两边组成的角叫做三角形的内角,它们的和是180 °
2.三角形按边分类,可以分成哪几类?
两边相等的等腰三角形
三边相等的等腰三角形
等边三角形
三角形
等腰三角形
三边不等的三角形
按边分
不等边三角形
课堂导入
上节课我们学习了三角形的内角,知道了三角形的三个内角和是180°.请大家观察下面的图形中的角.∠ACD是三角形的内角吗?
A
D
C
B
?
内角
内角
新知探究
如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫作三角形的外角.
A
B
C
D
(
∠ACD是△ABC的一个外角
与外角∠ACD不相邻的内角
与外角∠ACD相邻的内角
知识点1 三角形的外角及性质
新知探究
(
(
(
(
(
(
A
B
C
1
2
3
4
5
6
A
B
C
问题1:△ABC如图所示,请画出△ABC的所有外角,指出来有哪几个.
有6个,它们是∠1, ∠2, ∠3, ∠4, ∠5, ∠6.
问题2:△ABC的6个外角有什么关系
∠1和∠4, 是对顶角,相等;
∠2和∠5, 是对顶角,相等;
∠3和∠6, 是对顶角,相等.
知识点1 三角形的外角及性质
新知探究
问题3:在图中,外角∠ACD与它不相邻的内角∠A,∠B之间有什么大小关系?
解:∵∠ACD+∠ACB = 180°,(补角的定义)
∠A +∠B +∠ACB = 180°,(三角形的内角和定理)
∴∠ACD-∠A-∠B = 0.
∴∠ACD =∠A +∠B.
∵∠A>0,∠B>0,
∴∠ACD>∠A,∠ACD>∠B.
知识点1 三角形的外角及性质
新知探究
三角形的外角的性质
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于与它不相邻的任意一个内角.
归纳
知识点1 三角形的外角及性质
新知探究
∠C
∠3
∠DAC
∠4
练一练 1.如图,口答:
(1)∠1 = + ;
(2)∠2 = + .
B
A
C
D
1
2
3
4
知识点1 三角形的外角及性质
新知探究
练一练 2.如图,说出图形中∠1 的度数.
(1) (2)
(3) (4)
30°
60°
1
35°
60°
1
45°
50°
1
30°
15°
1
知识点1 三角形的外角及性质
新知探究
例1 如图,∠BCD=92°,∠A=27°,∠BED=44°,求:
(1) ∠B的度数;(2) ∠BFD的度数;
A
C
D
E
B
解:(1) 在△ABC中,∵ ∠BCD=∠A+∠B(三角形的一个外角等于与它不相邻的两个内角的和),
∠BCD=92°,∠A=27°,(已知)
∴∠B=∠BCD-∠A=92°-27°=65°;
(2) 在△BEF中,∵ ∠BFD=∠B+∠BED(三角形的一个外角等于与它不相邻的两个内角的和),
∠BED=44°,∠B=65°,(已知)
∴∠BFD=44°+65°=109°.
知识点1 三角形的外角及性质
F
新知探究
练一练 如图,∠BAE,∠CBF,∠ACD 是△ABC 的三个外角,它们的和是多少?
解法一:
∵ ∠BAE =∠2 +∠3,
∠CBF =∠1 +∠3,
∠ACD =∠1 +∠2,
∴ ∠BAE +∠CBF +∠ACD
= (∠2 +∠3)+(∠1 +∠3)+ (∠1 +∠2)
A
B
F
C
D
E
1
2
3
= 2(∠1 +∠2 +∠3).
∵ ∠1 +∠2 +∠3 =180°,
∴ ∠BAE +∠CBF +∠ACD = 2×180°=360°.
知识点1 三角形的外角及性质
新知探究
A
B
F
C
D
E
1
2
3
由∠1 + ∠2 + ∠3 =180°,
得∠BAE + ∠CBF + ∠ACD
= 540°- 180°
=360°.
解法二:
由∠1 +∠BAE =180°,
∠2 +∠CBF =180°,
∠3 +∠ACD =180°,
得∠1 +∠2 +∠3 + ∠BAE+∠CBF +∠ACD = 540°.
归纳:三角形的外角和360°.
知识点1 三角形的外角及性质
新知探究
谈一谈
1.一个三角形的内角最多有几个直角,最多有几个钝角?
2.一个三角形能不能三个内角都是锐角?
知识点2 三角形按角分类
新知探究
问题4:按照三角形内角的大小,三角形可以分为哪几类?
锐角三角形
直角三角形
钝角三角形.
三个内角都是锐角的三角形
有一个内角是直角的三角形
有一个内角是钝角的三角形
知识点2 三角形按角分类
新知探究
请你试着以角为标准对三角形进行分类
两边相等的等腰三角形
三边相等的等腰三角形
三角形
按角分
锐角三角形
直角三角形
钝角三角形
等腰直角三角形
等边三角形
三角形
等腰三角形
三边不等的三角形
按边分
不等边三角形
知识点2 三角形按角分类
随堂练习
1.如果三角形三个外角度数之比是3:4:5,则此三角形一定是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
2.已知,如图,△ABC 中,∠B=∠DAC,则∠BAC 和∠ADC的关系是( )
A.∠BAC<∠ADC B.∠BAC=∠ADC
C.∠BAC>∠ADC D.不能确定
B
B
3.如图,AB//CD,∠A=37°, ∠C=63°,那么∠F
等于( )
F
A
B
E
C
D
A.26°
B.63°
C.37°
D.60°
A
A
B
C
D
E
1
2
F
G
解:∵∠1是△FBE的外角,
∴∠1=∠B+ ∠E,
同理∠2=∠A+∠D.
在△CFG中 ,
∠C+∠1+∠2=180 ,
∴∠A+ ∠ B+∠C+ ∠ D+∠E= 180 .
4.如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
拓展提升
下面给出的四个三角形都有一部分被遮挡,其中不能判断三角形类型的是( )
C
1
2
一个零件的形状如图所示,按规定∠A 应等于90°,
∠B 和∠C 分别是21°和20°,质量检验员量得∠BDC=
130°后就断定这个零件不合格.请说明为什么?
如图,在△ABC 中,D 为BC 的延长线上一点,∠A=60°,
∠ABC 和∠ACD 的平分线交于点O,求∠O 的度数.
由题意得∠OBC= ∠ABC,
∠DCO= ∠ACD,
∴∠O=∠DCO-∠OBC= ∠ACD- ∠ABC=
(∠ACD-∠ABC )= ∠A=30°.
解:
3
如图,连接AD 并延长到点E,
则∠CDE=∠C+∠2,
∠BDE=∠B+∠1.
所以∠CDE+∠BDE=∠C+∠2+∠B+∠1.
即∠BDC=∠C+∠B+∠CAB.
若零件合格,则∠BDC=20°+21°+90°=131°.
而量得∠BDC=130°,所以这个零件不合格.
解:
归纳小结
三角形的外角
三角形外角的性质
三角形的分类
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于与它不相邻的任意一个内角.
按边分类
按角分类
等腰三角形
不等边三角形
锐角三角形
直角三角形
钝角三角形
新知探究
例2 (一题多解)如图,计算∠BDC.
A
B
C
D
(
(
(
51 °
20 °
30 °
解:(解法一)连接AD并延长于点E.
在△ABD中,∠1+∠ABD=∠3,
在△ACD中,∠2+∠ACD=∠4.
因为∠BDC=∠3+∠4,∠BAC=∠1+∠2,
所以∠BDC=∠BAC+∠ABD+∠ACD
=51° +20°+30°=101°.
(解法二)延长BD交AC于点E.
在△ABE中,∠1=∠ABE+∠BAE,
在△ECD中,∠BDC=∠1+∠ECD.
所以∠BDC=∠BAC+∠ABD+∠ACD
=51° +20°+30°=101°.
知识点1 三角形的外角及性质
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
