冀教版(2024)七年级数学下册 7.6图形的平移 课件(共17张PPT)
文档属性
| 名称 | 冀教版(2024)七年级数学下册 7.6图形的平移 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 00:00:00 | ||
图片预览

文档简介
(共17张PPT)
7.6 图形的平移
一
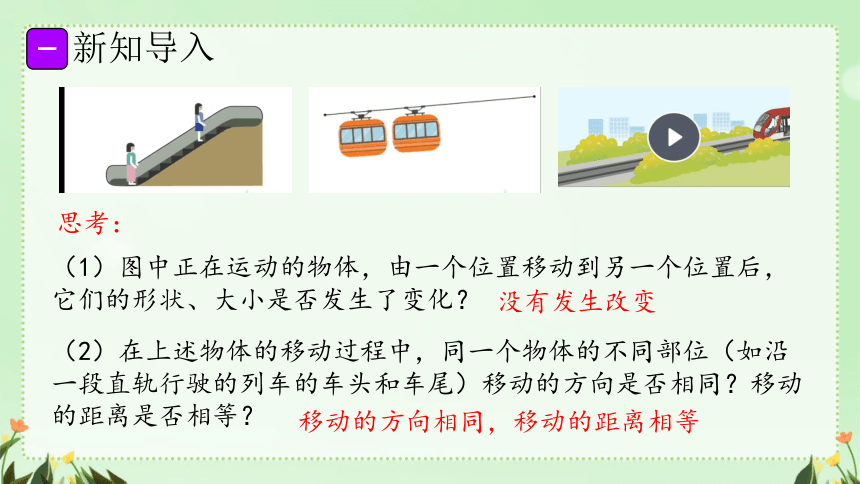
新知导入
(1)图中正在运动的物体,由一个位置移动到另一个位置后,它们的形状、大小是否发生了变化?
(2)在上述物体的移动过程中,同一个物体的不同部位(如沿一段直轨行驶的列车的车头和车尾)移动的方向是否相同?移动的距离是否相等?
思考:
没有发生改变
移动的方向相同,移动的距离相等
二
新知探究
A'
B'
C'
D'
A
B
C
D
A
B
C
D
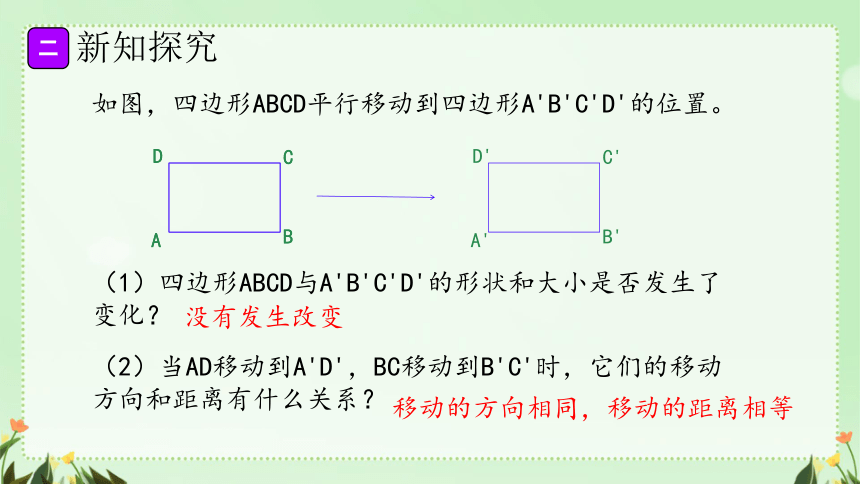
如图,四边形ABCD平行移动到四边形A'B'C'D'的位置。
(1)四边形ABCD与A'B'C'D'的形状和大小是否发生了变化?
(2)当AD移动到A'D',BC移动到B'C'时,它们的移动方向和距离有什么关系?
没有发生改变
移动的方向相同,移动的距离相等
小结
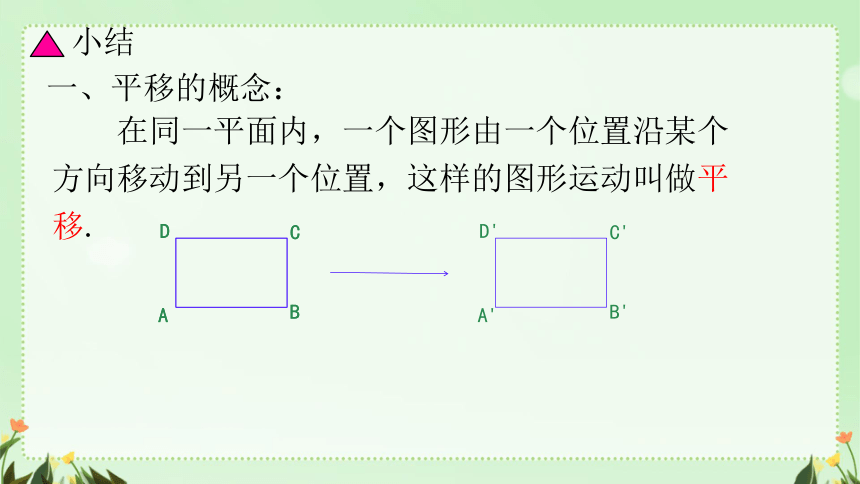
一、平移的概念:
在同一平面内,一个图形由一个位置沿某个方向移动到另一个位置,这样的图形运动叫做平移.
A'
B'
C'
D'
A
B
C
D
A
B
C
D
小结
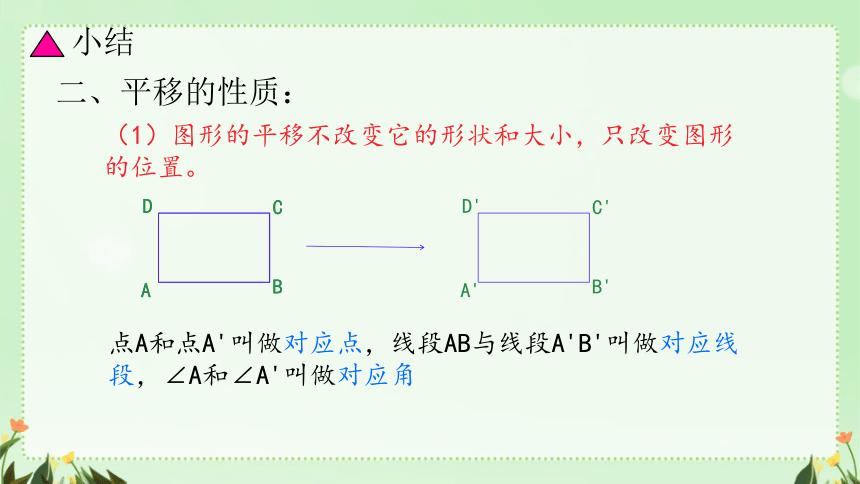
二、平移的性质:
A'
B'
C'
D'
A
B
C
D
A
B
C
D
(1)图形的平移不改变它的形状和大小,只改变图形的位置。
点A和点A'叫做对应点,线段AB与线段A'B'叫做对应线段,∠A和∠A'叫做对应角
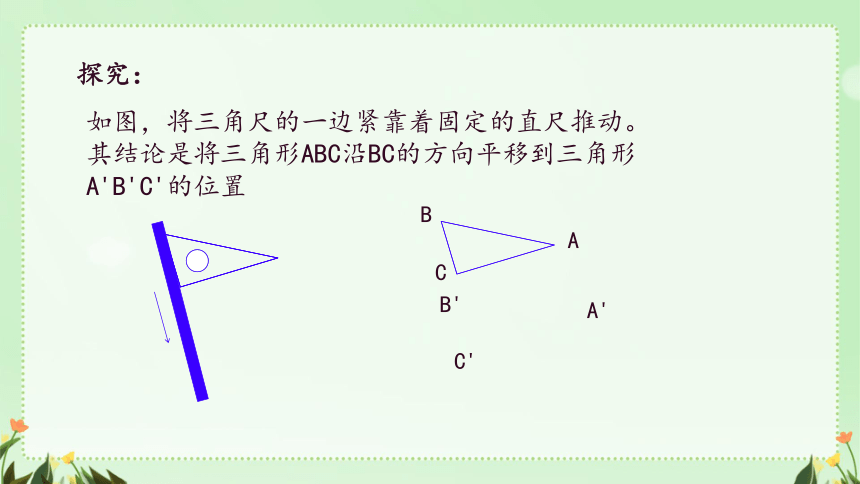
探究:
如图,将三角尺的一边紧靠着固定的直尺推动。
其结论是将三角形ABC沿BC的方向平移到三角形A'B'C'的位置
B
C
A
A'
B'
C'
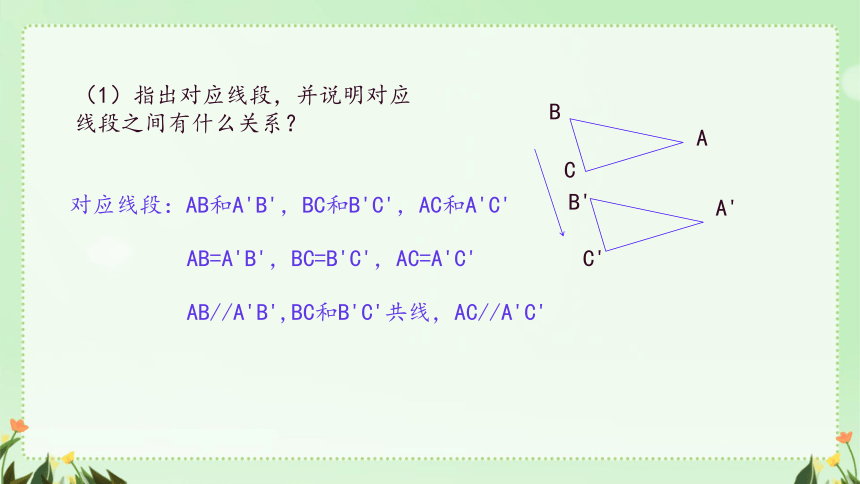
(1)指出对应线段,并说明对应线段之间有什么关系?
B
C
A
A'
B'
C'
对应线段:AB和A'B',BC和B'C',AC和A'C'
AB=A'B',BC=B'C',AC=A'C'
AB//A'B',BC和B'C'共线,AC//A'C'
(2)指出对应角,并说明对应角之间有什么关系?
B
C
A
A'
B'
C'
对应角:
∠A和∠A',∠B和∠B',∠C和∠C'
∠A=∠A',∠B=∠B',∠C=∠C'
(3)对应点的连线AA',BB',CC',之间具有什么位置关系和数量关系?
B
C
A
A'
B'
C'
AA'//BB'//CC',BB'和CC'共线
AA'=BB'=CC'
性质(2)在同一平面内,一个图形平移后得到的图形与原图形的对应线段平行(或在同一条直线上)且相等,对应角相等,各对应点所连接的线段平行(或在同一条直线上)且相等。
注意:
①由平移定义可知,平移图形只改变图形的位置,不改变图形的形状、大小。
②平移得到的图形与原图形中的对应线段平行(或共线)且相等:对应角相等:对应点连线平行(或共线)且相等。
③“将一个图形沿某一个方向移动一定的距离”意味着“图形上的每一个点都沿同一方向移动了相同距离”。
三、平移作图法:(两种方法)
例1、如图,网格图中小方格都是边长为1个单位长度的小正方形。
(1)请你画出将三角形 ABC 向右平移5个单位长度后的图形。连接各对对应点,并指出相等的线段和相等的角。
①分析画图要求,找出平移方向和平移距离;
②分析所作图形,找出构成图形的关键点;
③沿一定的方向,按一定距离平移各个关键点;
④连接所作的各个关键点;
⑤写出结论。
相等的线段分为两类:
对应线段相等,即 AB = A'B', BC = B'C', AC = A'C'
对应角相等,即∠ABC=∠A'B'C',∠ACB=∠A'C'B',∠BAC=∠B'A'C'
对应点所连接的线段相等,即 AA'= BB'= CC'
(2)请指出图中(包括新画出的)所有分别互相平行的线段。平行的线段也分为两类:
对应线段平行,即 AB//A'B',BC//B'C',AC//A'C'
对应点所连接的线段平行,即 AA'// BB'//CC'
例2、在网格图中,把四边形 ABCD 按箭头指示的方向平移,并使点 A 移到箭头标示的格点处,请你画出平移后的图形。
①找出图形的关键点;
②将原图中的关键点与移动后该位置的对应点连接起来;
③过其他关键点分别作线段使之与②所连线段平行且相等;
④再连接这些关键点的对应点,所得图形就是平移原图形所得的新图形。
四
课堂总结
7.6 图形的平移
一
新知导入
(1)图中正在运动的物体,由一个位置移动到另一个位置后,它们的形状、大小是否发生了变化?
(2)在上述物体的移动过程中,同一个物体的不同部位(如沿一段直轨行驶的列车的车头和车尾)移动的方向是否相同?移动的距离是否相等?
思考:
没有发生改变
移动的方向相同,移动的距离相等
二
新知探究
A'
B'
C'
D'
A
B
C
D
A
B
C
D
如图,四边形ABCD平行移动到四边形A'B'C'D'的位置。
(1)四边形ABCD与A'B'C'D'的形状和大小是否发生了变化?
(2)当AD移动到A'D',BC移动到B'C'时,它们的移动方向和距离有什么关系?
没有发生改变
移动的方向相同,移动的距离相等
小结
一、平移的概念:
在同一平面内,一个图形由一个位置沿某个方向移动到另一个位置,这样的图形运动叫做平移.
A'
B'
C'
D'
A
B
C
D
A
B
C
D
小结
二、平移的性质:
A'
B'
C'
D'
A
B
C
D
A
B
C
D
(1)图形的平移不改变它的形状和大小,只改变图形的位置。
点A和点A'叫做对应点,线段AB与线段A'B'叫做对应线段,∠A和∠A'叫做对应角
探究:
如图,将三角尺的一边紧靠着固定的直尺推动。
其结论是将三角形ABC沿BC的方向平移到三角形A'B'C'的位置
B
C
A
A'
B'
C'
(1)指出对应线段,并说明对应线段之间有什么关系?
B
C
A
A'
B'
C'
对应线段:AB和A'B',BC和B'C',AC和A'C'
AB=A'B',BC=B'C',AC=A'C'
AB//A'B',BC和B'C'共线,AC//A'C'
(2)指出对应角,并说明对应角之间有什么关系?
B
C
A
A'
B'
C'
对应角:
∠A和∠A',∠B和∠B',∠C和∠C'
∠A=∠A',∠B=∠B',∠C=∠C'
(3)对应点的连线AA',BB',CC',之间具有什么位置关系和数量关系?
B
C
A
A'
B'
C'
AA'//BB'//CC',BB'和CC'共线
AA'=BB'=CC'
性质(2)在同一平面内,一个图形平移后得到的图形与原图形的对应线段平行(或在同一条直线上)且相等,对应角相等,各对应点所连接的线段平行(或在同一条直线上)且相等。
注意:
①由平移定义可知,平移图形只改变图形的位置,不改变图形的形状、大小。
②平移得到的图形与原图形中的对应线段平行(或共线)且相等:对应角相等:对应点连线平行(或共线)且相等。
③“将一个图形沿某一个方向移动一定的距离”意味着“图形上的每一个点都沿同一方向移动了相同距离”。
三、平移作图法:(两种方法)
例1、如图,网格图中小方格都是边长为1个单位长度的小正方形。
(1)请你画出将三角形 ABC 向右平移5个单位长度后的图形。连接各对对应点,并指出相等的线段和相等的角。
①分析画图要求,找出平移方向和平移距离;
②分析所作图形,找出构成图形的关键点;
③沿一定的方向,按一定距离平移各个关键点;
④连接所作的各个关键点;
⑤写出结论。
相等的线段分为两类:
对应线段相等,即 AB = A'B', BC = B'C', AC = A'C'
对应角相等,即∠ABC=∠A'B'C',∠ACB=∠A'C'B',∠BAC=∠B'A'C'
对应点所连接的线段相等,即 AA'= BB'= CC'
(2)请指出图中(包括新画出的)所有分别互相平行的线段。平行的线段也分为两类:
对应线段平行,即 AB//A'B',BC//B'C',AC//A'C'
对应点所连接的线段平行,即 AA'// BB'//CC'
例2、在网格图中,把四边形 ABCD 按箭头指示的方向平移,并使点 A 移到箭头标示的格点处,请你画出平移后的图形。
①找出图形的关键点;
②将原图中的关键点与移动后该位置的对应点连接起来;
③过其他关键点分别作线段使之与②所连线段平行且相等;
④再连接这些关键点的对应点,所得图形就是平移原图形所得的新图形。
四
课堂总结
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
