华东师大版九年级数学上册23.3.2相似三角形的判定教学设计(2课时)
文档属性
| 名称 | 华东师大版九年级数学上册23.3.2相似三角形的判定教学设计(2课时) |  | |
| 格式 | docx | ||
| 文件大小 | 268.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 16:24:04 | ||
图片预览




文档简介
2.相似三角形的判定
第1课时 相似三角形的判定定理1
1.通过类比和猜想掌握两个三角形相似的判定定理.
2.能够运用角角相等来解决简单问题.
3.在探索过程中,进一步发展学生的探究、交流能力,以及动手、动脑的习惯.
重点:掌握两个三角形相似的判定定理1.
难点:探索三角形相似的判定方法.
1.(1)相似三角形的判定方法:定义法、平行法;
(2)判定两个三角形全等的方法有
①两边及夹角(SAS);
②两角及夹边(ASA);
③两角及对边(AAS);
④三边(SSS);
⑤直角三角形的斜边直角边(H.L.).
2.让我们先从最常见的三角尺开始.
观察你和老师的直角三角尺,同样角度(30°与60°,或45°与45°)的三角尺看起来是相似吗 这样从直观来看,一个三角形的三个角分别与另一个三角形的三个角对应相等时,它们就“应该”相似了.确实是这样吗
问题1:任意画两个三角形,使其三对角分别对应相等.用刻度尺量一量两个三角形的对应边,看看两个三角形的对应边是否成比例.你能得出什么结论
解:画△ABC和△A'B'C',使∠A=∠A',∠B=∠B',∠C=∠C'.
经测量==,
所以△ABC≌△A'B'C'.
[归纳] 三角形相似判定定理1:两角分别相等的两个三角形相似.
符号语言:因为∠A=∠A',∠B=∠B',所以△ABC∽△A'B'C'(两角对应相等的两三角形相似)
问题2:如图所示,在△ABC和△A1B1C1中,∠A=∠A1,∠B=∠B1.求证:△ABC∽△A1B1C1.
证明:在AB上截取AD=A1B1,过D点作DE∥BC交AC于点E,则△ADE∽△ABC.
因为DE∥BC,
所以∠ADE=∠B.
又∠B=∠B1,
所以∠ADE=∠B1.
在△ADE和△A1B1C1中,
因为∠A=∠A1,AD=A1B1,∠ADE=∠B1,
所以△ADE≌△A1B1C1.
所以△ABC∽△A1B1C1.
追问学生:如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似
范例应用
例1 如图所示,在Rt△ABC和 Rt△A'B'C' 中,∠C=∠C'=90°,∠A=∠A',证明:△ABC∽△A'B'C'.
证明:因为∠C=∠C'=90°,
∠A=∠A',
所以△ABC∽△A'B'C'(如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似).
例2 如图所示,在△ABC中,DE∥BC,EF∥AB.求证:△ADE∽△EFC.
证明:因为DE∥BC,
所以∠AED=∠C.
又因为EF∥AB,
所以∠A=∠FEC.
所以△ADE∽△EFC.
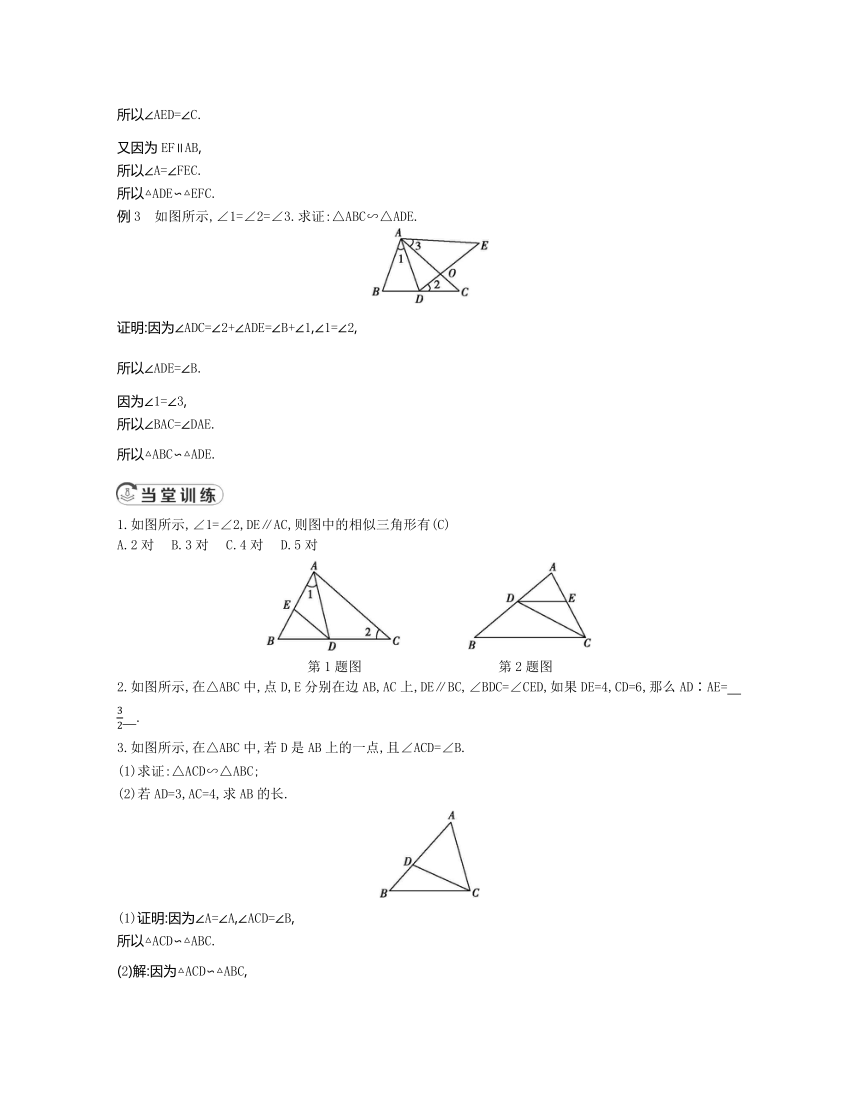
例3 如图所示,∠1=∠2=∠3.求证:△ABC∽△ADE.
证明:因为∠ADC=∠2+∠ADE=∠B+∠1,∠1=∠2,
所以∠ADE=∠B.
因为∠1=∠3,
所以∠BAC=∠DAE.
所以△ABC∽△ADE.
1.如图所示,∠1=∠2,DE∥AC,则图中的相似三角形有(C)
A.2对 B.3对 C.4对 D.5对
第1题图 第2题图
2.如图所示,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,∠BDC=∠CED,如果DE=4,CD=6,那么AD∶AE= .
3.如图所示,在△ABC中,若D是AB上的一点,且∠ACD=∠B.
(1)求证:△ACD∽△ABC;
(2)若AD=3,AC=4,求AB的长.
(1)证明:因为∠A=∠A,∠ACD=∠B,
所以△ACD∽△ABC.
(2)解:因为△ACD∽△ABC,
所以=,即=.
所以AB=.
4.如图所示,在△ABC中,∠C=90°,DE⊥AB于点E,DF⊥BC于点F,DF交AB于点H.求证:△DEH∽△BCA.
证明:因为DE⊥AB,DF⊥BC,
所以∠D+∠DHE=∠B+∠BHF=90°.
因为∠BHF=∠DHE,
所以∠D=∠B.
又因为∠DEH=∠C=90°,
所以△DEH∽△BCA.
相似三角形判定方法:
1.相似三角形定义(很少用)
2.用平行线证明三角形相似(很好用)
3.两角分别相等的两个三角形相似(注意隐含的公共角、对顶角)
2 相似三角形的判定
第1课时 相似三角形的判定定理1
1.定理:两角分别相等的两个三角形相似.
2.符号语言:
如图所示,因为∠A =∠D,∠B= ∠E,
所以△ABC∽△DEF.
本节运用类比的数学方法,在新概念提出、新知识点的讲授过程中,可以使学生易于理解和掌握.如学生在接受判定定理1时,由全等的判定类比到相似的判定,从而使得学生接受新的概念时显得轻松自然,容易理解.
第2课时 相似三角形的判定定理2,3
1.理解、掌握相似三角形的判定定理2,3.
2.能依据条件,灵活运用三种判定方法,正确判断两个三角形相似.
重点:灵活运用三种判定方法,正确判断两个三角形相似.
难点:探索三角形相似的判定方法.
三角形相似的判定方法:
1.平行线判定三角形相似:
平行于三角形一边的直线,和其他两边(或两边的延长线)相交所构成的三角形与原三角形相似.
2.三角形相似的判定定理1:
两角分别相等的两个三角形相似.
问题1:观察如图所示,如果有一点E在边AC上,那么点E应该在什么位置才能使△ADE∽△ABC
图中两个三角形的一组对应边AD与AB的长度的比值为 .将点E由点A开始在AC上移动,可以发现当AE= AC时,△ADE与△ABC似乎相似.此时= .
猜想:如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.
已知:如图所示,在△ABC和△A1B1C1中,∠A=∠A1,=,求证:△ABC∽△A1B1C1.
证明:在边AB上截取AD=A1B1,过点D作DE∥BC交AC于E,则△ADE∽△ABC.
所以=.
因为=且AD=A1B1,
所以AE=A1C1.
在△ADE和△A1B1C1中,AD=A1B1,∠A=∠A1,AE=A1C1,
所以△ADE≌△A1B1C1.
所以△ABC∽△A1B1C1.
[归纳] 相似三角形的判定定理2:
如果一个三角形的两边长与另一个三角形的两边长对应成比例,并且夹角相等,那么这两个三角形相似.
符号语言:因为A'B'∶AB=A'C'∶AC,∠A=∠A',
所以△A'B'C'∽△ABC(两边对应成比例且夹角相等,两个三角形相似).
范例应用
例1 判断图中△AEB和△FEC是否相似
解:因为==,==,
所以=.
因为∠AEB=∠FEC,
所以△AEB∽△FEC.
[方法归纳] 运用两边成比例且夹角相等判断两个三角形相似时,找出对应边,计算对应边的比,注意隐含条件(对顶角、公共角).
例2 如图所示,△ABC与△ADE都是等腰三角形,AD=AE,AB=AC,∠DAB=∠CAE.求证:△ABC∽△ADE.
证明:因为AD=AE,AB=AC,
所以=.
因为∠DAB=∠CAE,
所以∠DAB+∠BAE=∠CAE+∠BAE,
即∠DAE=∠BAC.
所以△ABC∽△ADE.
问题2:如图所示,网格图中每个方格都是边长为1的正方形.若A,B,C,D,E,F都是格点,则△ABC与△DEF相似吗
解:因为AC=,BC==,AB=4,DF==2,EF==2,
ED=8,所以===.
由量角器测量得∠A=∠D,∠B=∠E,∠C=∠F.
所以△ABC∽△DEF.
[归纳] 相似三角形的判定定理3:三边成比例的两个三角形相似.
范例应用
例3 在△ABC和△A'B'C'中,AB=6 cm,BC=8 cm,AC=10 cm,A'B'=18 cm,B'C'=24 cm,A'C'=30 cm.试证明△ABC与△A'B'C'相似.
证明:因为AB=6 cm,BC=8 cm,AC=10 cm,A'B'=18 cm,B'C'=24 cm,A'C'=30 cm,
因为==,==,==,
所以==.
所以△ABC∽△A'B'C'.
[方法归纳] 恰当选择相似三角形的判定方法:如果知道一组角相等,选择两角相等或两边成比例夹角相等;如果知道边成比例,选择三边成比例或两边成比例且夹角相等;知道平行线,选择平行线法.
1.如图所示,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的(C)
A.= B.= C.= D.=
第1题图 第2题图
2.如图所示,在正方形网格上,与△ABC相似的三角形是(A)
A.△AFD B.△AED C.△FED D.不能确定
3.要做甲、乙两个形状相同的三角形框架,已知三角形框架甲的三边长分别为50 cm,60 cm,80 cm,三角形框架乙的一边长为20 cm,那么符合条件的三角形框架乙共有(C)
A.1种 B.2种 C.3种 D.4种
4.如图所示,D是△ABC的边AB上一点,要使△ACD∽△ABC,则它们必须具备的条件是(D)
A.= B.= C.CD2=AD·DB D.AC2=AD·AB
第4题图 第5题图
5.如图所示,在△ABC中,点D,E分别为边AB,AC上的点,试添加一个条件: =(答案不唯一) ,使得△ADE与△ABC相似.(任意写出一个满足条件的即可)
6.如图所示,四边形ABDC,CDFE,EFHG都是正方形.求证:
(1)△ADF∽△HDA;
(2)∠AFB+∠AHB=45°.
证明:(1)设正方形ABDC,CDFE,EFHG的边长为1,则AD=,DF=1,DH=2.
因为=,
所以=.
又因为∠ADF=∠HDA,
所以△ADF∽△HDA.
(2)因为△ADF∽△HDA,
所以∠AHB=∠DAF.
因为四边形ABDC是正方形,
所以AB=BD,△ABD是等腰直角三角形.
所以∠ADB=45°.
又因为∠ADB=∠DAF+∠AFD,
所以∠AFB+∠AHB=45°.
相似三角形的判定方法
一、相似三角形的判定定理2
1.定理:两边成比例且夹角相等的两个三角形相似.
2.符号语言:如下图所示,
因为=,∠A=∠ D,
所以△ABC∽△DEF.
二、相似三角形的判定定理3
1.定理:三边成比例的两个三角形相似.
2.符号语言:如上图所示,
因为==,
所以△ABC∽△DEF.
第2课时 相似三角形的判定定理2,3
1.相似三角形的判定定理2
2.相似三角形的判定定理3
本节课主要是探究相似三角形的判定定理2,3,由于上节课已经学习了探究两个三角形相似的判定定理1,而本节课内容在探究方法上又具有一定的相似性,因此本教学设计注意方法上的“新旧联系”,以帮助学生形成认知上的正迁移.此外,由于判定定理2的条件“相应的夹角相等”在应用中容易让学生忽视,所以教学设计采用了“小组讨论+集中展示反例”的学习形式来加深学生的印象.
第1课时 相似三角形的判定定理1
1.通过类比和猜想掌握两个三角形相似的判定定理.
2.能够运用角角相等来解决简单问题.
3.在探索过程中,进一步发展学生的探究、交流能力,以及动手、动脑的习惯.
重点:掌握两个三角形相似的判定定理1.
难点:探索三角形相似的判定方法.
1.(1)相似三角形的判定方法:定义法、平行法;
(2)判定两个三角形全等的方法有
①两边及夹角(SAS);
②两角及夹边(ASA);
③两角及对边(AAS);
④三边(SSS);
⑤直角三角形的斜边直角边(H.L.).
2.让我们先从最常见的三角尺开始.
观察你和老师的直角三角尺,同样角度(30°与60°,或45°与45°)的三角尺看起来是相似吗 这样从直观来看,一个三角形的三个角分别与另一个三角形的三个角对应相等时,它们就“应该”相似了.确实是这样吗
问题1:任意画两个三角形,使其三对角分别对应相等.用刻度尺量一量两个三角形的对应边,看看两个三角形的对应边是否成比例.你能得出什么结论
解:画△ABC和△A'B'C',使∠A=∠A',∠B=∠B',∠C=∠C'.
经测量==,
所以△ABC≌△A'B'C'.
[归纳] 三角形相似判定定理1:两角分别相等的两个三角形相似.
符号语言:因为∠A=∠A',∠B=∠B',所以△ABC∽△A'B'C'(两角对应相等的两三角形相似)
问题2:如图所示,在△ABC和△A1B1C1中,∠A=∠A1,∠B=∠B1.求证:△ABC∽△A1B1C1.
证明:在AB上截取AD=A1B1,过D点作DE∥BC交AC于点E,则△ADE∽△ABC.
因为DE∥BC,
所以∠ADE=∠B.
又∠B=∠B1,
所以∠ADE=∠B1.
在△ADE和△A1B1C1中,
因为∠A=∠A1,AD=A1B1,∠ADE=∠B1,
所以△ADE≌△A1B1C1.
所以△ABC∽△A1B1C1.
追问学生:如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似
范例应用
例1 如图所示,在Rt△ABC和 Rt△A'B'C' 中,∠C=∠C'=90°,∠A=∠A',证明:△ABC∽△A'B'C'.
证明:因为∠C=∠C'=90°,
∠A=∠A',
所以△ABC∽△A'B'C'(如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似).
例2 如图所示,在△ABC中,DE∥BC,EF∥AB.求证:△ADE∽△EFC.
证明:因为DE∥BC,
所以∠AED=∠C.
又因为EF∥AB,
所以∠A=∠FEC.
所以△ADE∽△EFC.
例3 如图所示,∠1=∠2=∠3.求证:△ABC∽△ADE.
证明:因为∠ADC=∠2+∠ADE=∠B+∠1,∠1=∠2,
所以∠ADE=∠B.
因为∠1=∠3,
所以∠BAC=∠DAE.
所以△ABC∽△ADE.
1.如图所示,∠1=∠2,DE∥AC,则图中的相似三角形有(C)
A.2对 B.3对 C.4对 D.5对
第1题图 第2题图
2.如图所示,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,∠BDC=∠CED,如果DE=4,CD=6,那么AD∶AE= .
3.如图所示,在△ABC中,若D是AB上的一点,且∠ACD=∠B.
(1)求证:△ACD∽△ABC;
(2)若AD=3,AC=4,求AB的长.
(1)证明:因为∠A=∠A,∠ACD=∠B,
所以△ACD∽△ABC.
(2)解:因为△ACD∽△ABC,
所以=,即=.
所以AB=.
4.如图所示,在△ABC中,∠C=90°,DE⊥AB于点E,DF⊥BC于点F,DF交AB于点H.求证:△DEH∽△BCA.
证明:因为DE⊥AB,DF⊥BC,
所以∠D+∠DHE=∠B+∠BHF=90°.
因为∠BHF=∠DHE,
所以∠D=∠B.
又因为∠DEH=∠C=90°,
所以△DEH∽△BCA.
相似三角形判定方法:
1.相似三角形定义(很少用)
2.用平行线证明三角形相似(很好用)
3.两角分别相等的两个三角形相似(注意隐含的公共角、对顶角)
2 相似三角形的判定
第1课时 相似三角形的判定定理1
1.定理:两角分别相等的两个三角形相似.
2.符号语言:
如图所示,因为∠A =∠D,∠B= ∠E,
所以△ABC∽△DEF.
本节运用类比的数学方法,在新概念提出、新知识点的讲授过程中,可以使学生易于理解和掌握.如学生在接受判定定理1时,由全等的判定类比到相似的判定,从而使得学生接受新的概念时显得轻松自然,容易理解.
第2课时 相似三角形的判定定理2,3
1.理解、掌握相似三角形的判定定理2,3.
2.能依据条件,灵活运用三种判定方法,正确判断两个三角形相似.
重点:灵活运用三种判定方法,正确判断两个三角形相似.
难点:探索三角形相似的判定方法.
三角形相似的判定方法:
1.平行线判定三角形相似:
平行于三角形一边的直线,和其他两边(或两边的延长线)相交所构成的三角形与原三角形相似.
2.三角形相似的判定定理1:
两角分别相等的两个三角形相似.
问题1:观察如图所示,如果有一点E在边AC上,那么点E应该在什么位置才能使△ADE∽△ABC
图中两个三角形的一组对应边AD与AB的长度的比值为 .将点E由点A开始在AC上移动,可以发现当AE= AC时,△ADE与△ABC似乎相似.此时= .
猜想:如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.
已知:如图所示,在△ABC和△A1B1C1中,∠A=∠A1,=,求证:△ABC∽△A1B1C1.
证明:在边AB上截取AD=A1B1,过点D作DE∥BC交AC于E,则△ADE∽△ABC.
所以=.
因为=且AD=A1B1,
所以AE=A1C1.
在△ADE和△A1B1C1中,AD=A1B1,∠A=∠A1,AE=A1C1,
所以△ADE≌△A1B1C1.
所以△ABC∽△A1B1C1.
[归纳] 相似三角形的判定定理2:
如果一个三角形的两边长与另一个三角形的两边长对应成比例,并且夹角相等,那么这两个三角形相似.
符号语言:因为A'B'∶AB=A'C'∶AC,∠A=∠A',
所以△A'B'C'∽△ABC(两边对应成比例且夹角相等,两个三角形相似).
范例应用
例1 判断图中△AEB和△FEC是否相似
解:因为==,==,
所以=.
因为∠AEB=∠FEC,
所以△AEB∽△FEC.
[方法归纳] 运用两边成比例且夹角相等判断两个三角形相似时,找出对应边,计算对应边的比,注意隐含条件(对顶角、公共角).
例2 如图所示,△ABC与△ADE都是等腰三角形,AD=AE,AB=AC,∠DAB=∠CAE.求证:△ABC∽△ADE.
证明:因为AD=AE,AB=AC,
所以=.
因为∠DAB=∠CAE,
所以∠DAB+∠BAE=∠CAE+∠BAE,
即∠DAE=∠BAC.
所以△ABC∽△ADE.
问题2:如图所示,网格图中每个方格都是边长为1的正方形.若A,B,C,D,E,F都是格点,则△ABC与△DEF相似吗
解:因为AC=,BC==,AB=4,DF==2,EF==2,
ED=8,所以===.
由量角器测量得∠A=∠D,∠B=∠E,∠C=∠F.
所以△ABC∽△DEF.
[归纳] 相似三角形的判定定理3:三边成比例的两个三角形相似.
范例应用
例3 在△ABC和△A'B'C'中,AB=6 cm,BC=8 cm,AC=10 cm,A'B'=18 cm,B'C'=24 cm,A'C'=30 cm.试证明△ABC与△A'B'C'相似.
证明:因为AB=6 cm,BC=8 cm,AC=10 cm,A'B'=18 cm,B'C'=24 cm,A'C'=30 cm,
因为==,==,==,
所以==.
所以△ABC∽△A'B'C'.
[方法归纳] 恰当选择相似三角形的判定方法:如果知道一组角相等,选择两角相等或两边成比例夹角相等;如果知道边成比例,选择三边成比例或两边成比例且夹角相等;知道平行线,选择平行线法.
1.如图所示,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的(C)
A.= B.= C.= D.=
第1题图 第2题图
2.如图所示,在正方形网格上,与△ABC相似的三角形是(A)
A.△AFD B.△AED C.△FED D.不能确定
3.要做甲、乙两个形状相同的三角形框架,已知三角形框架甲的三边长分别为50 cm,60 cm,80 cm,三角形框架乙的一边长为20 cm,那么符合条件的三角形框架乙共有(C)
A.1种 B.2种 C.3种 D.4种
4.如图所示,D是△ABC的边AB上一点,要使△ACD∽△ABC,则它们必须具备的条件是(D)
A.= B.= C.CD2=AD·DB D.AC2=AD·AB
第4题图 第5题图
5.如图所示,在△ABC中,点D,E分别为边AB,AC上的点,试添加一个条件: =(答案不唯一) ,使得△ADE与△ABC相似.(任意写出一个满足条件的即可)
6.如图所示,四边形ABDC,CDFE,EFHG都是正方形.求证:
(1)△ADF∽△HDA;
(2)∠AFB+∠AHB=45°.
证明:(1)设正方形ABDC,CDFE,EFHG的边长为1,则AD=,DF=1,DH=2.
因为=,
所以=.
又因为∠ADF=∠HDA,
所以△ADF∽△HDA.
(2)因为△ADF∽△HDA,
所以∠AHB=∠DAF.
因为四边形ABDC是正方形,
所以AB=BD,△ABD是等腰直角三角形.
所以∠ADB=45°.
又因为∠ADB=∠DAF+∠AFD,
所以∠AFB+∠AHB=45°.
相似三角形的判定方法
一、相似三角形的判定定理2
1.定理:两边成比例且夹角相等的两个三角形相似.
2.符号语言:如下图所示,
因为=,∠A=∠ D,
所以△ABC∽△DEF.
二、相似三角形的判定定理3
1.定理:三边成比例的两个三角形相似.
2.符号语言:如上图所示,
因为==,
所以△ABC∽△DEF.
第2课时 相似三角形的判定定理2,3
1.相似三角形的判定定理2
2.相似三角形的判定定理3
本节课主要是探究相似三角形的判定定理2,3,由于上节课已经学习了探究两个三角形相似的判定定理1,而本节课内容在探究方法上又具有一定的相似性,因此本教学设计注意方法上的“新旧联系”,以帮助学生形成认知上的正迁移.此外,由于判定定理2的条件“相应的夹角相等”在应用中容易让学生忽视,所以教学设计采用了“小组讨论+集中展示反例”的学习形式来加深学生的印象.
