1.1 认识三角形 第4课时 三角形中的三条重要线段 课件(共30张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 1.1 认识三角形 第4课时 三角形中的三条重要线段 课件(共30张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 08:00:46 | ||
图片预览





文档简介
(共30张PPT)
鲁教版七年级上册数学
1 认识三角形
第4课时 三角形中的三条重要线段
学习目标
1.了解三角形的中线、高线和角平分线,了解重心的概念,会画出三角形的中线,知道三角形的三条中线交于一点(重心).
2.经历画、折等操作,得到几何直观图,观察并归纳得出数学结论,发展合情推理能力.
情境&导入
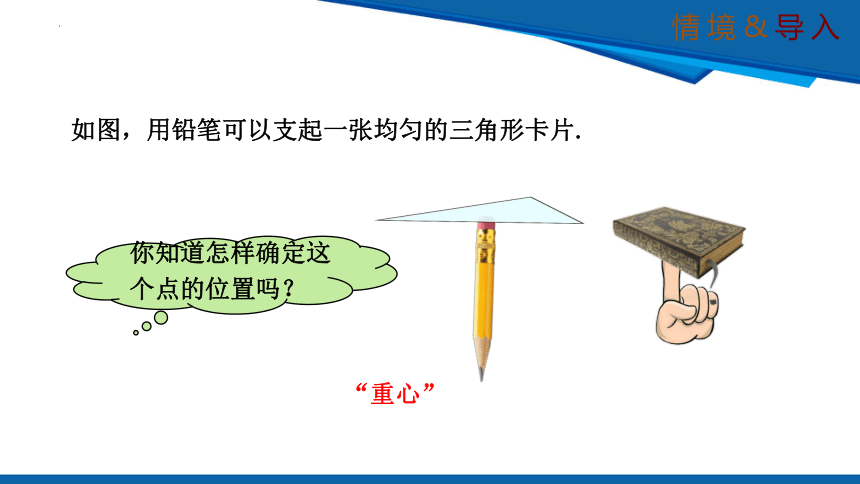
如图,用铅笔可以支起一张均匀的三角形卡片.
你知道怎样确定这个点的位置吗?
“重心”
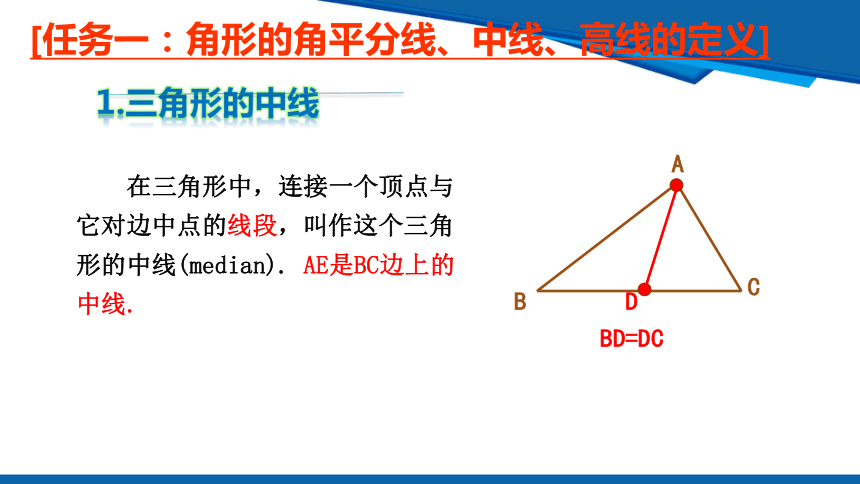
在三角形中,连接一个顶点与它对边中点的线段,叫作这个三角形的中线(median). AE是BC边上的中线.
BD=DC
B
C
D
A
1.三角形的中线
[任务一:角形的角平分线、中线、高线的定义]
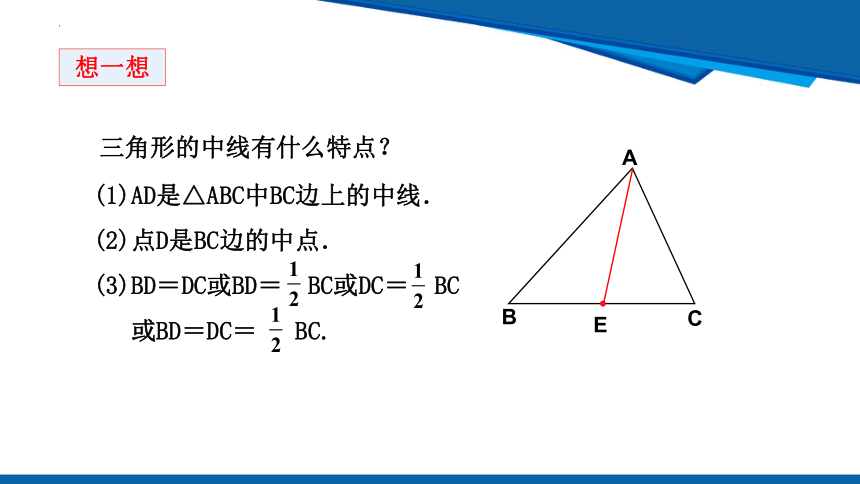
三角形的中线有什么特点?
A
B
C
E
(1)AD是△ABC中BC边上的中线.
(2)点D是BC边的中点.
(3)BD=DC或BD= BC或DC= BC
或BD=DC= BC.
想一想
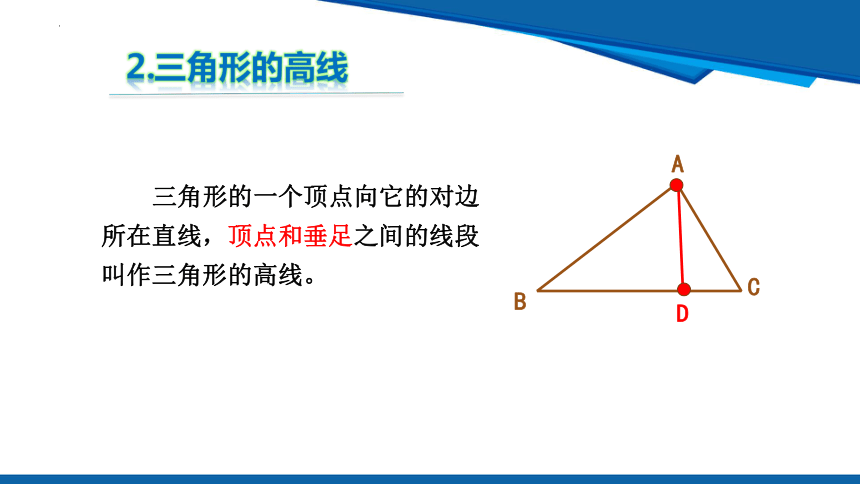
三角形的一个顶点向它的对边所在直线,顶点和垂足之间的线段叫作三角形的高线。
B
C
D
A
2.三角形的高线
三角形的高线有什么特点?
(1)AD是△ABC中BC边上的高线.
(2)∴∠AFB=∠CFB= 90 °.
想一想
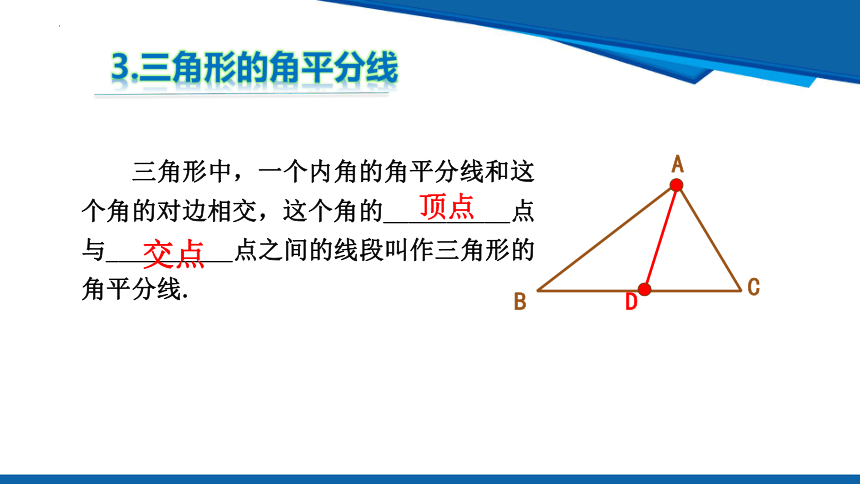
三角形中,一个内角的角平分线和这个角的对边相交,这个角的__________点与__________点之间的线段叫作三角形的角平分线.
B
C
D
A
3.三角形的角平分线
顶点
交点
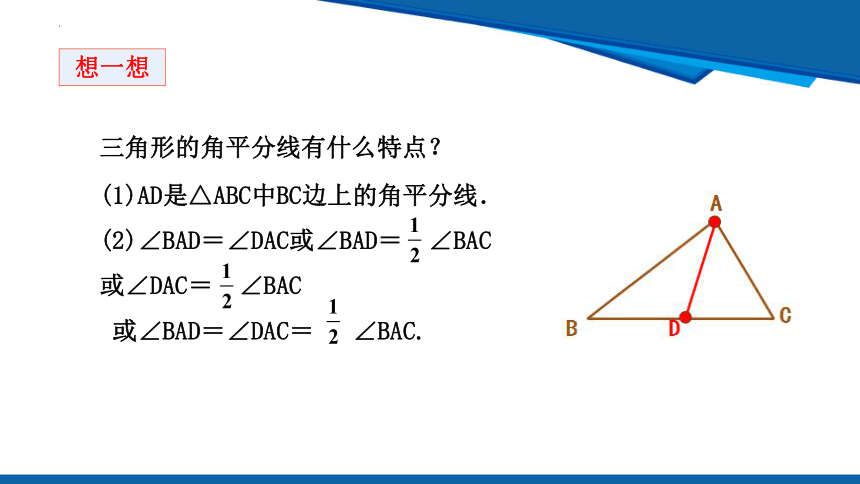
三角形的角平分线有什么特点?
(1)AD是△ABC中BC边上的角平分线.
(2)∠BAD=∠DAC或∠BAD= ∠BAC
或∠DAC= ∠BAC
或∠BAD=∠DAC= ∠BAC.
想一想
典题精析
例1.如图,在△ABC中,AD平分∠BAC且与BC相交于点D,∠B=40°,∠BAD=30°,则∠C的度数是多少?
解:∵AD平分∠BAC,
∴∠BAC=2∠BAD=2×30°=60°,
∴∠B+∠BAC+∠C=180°,
∴∠C=180°﹣∠B﹣∠BAC=180°﹣40°﹣60°=80°.
答:∠C的度数为80°
即时测评
1.如图,D,E分别为△ABC的边AC,BC的中点,则下列说法中不正确的是( )
A.DE是△BDC的中线 B.∠C的对边只有DE
C.BD是△ABC的中线 D.AD=DC,BE=EC
B
即时测评
2.如图,在△ABC中,∠A=60°,BO,CO平分∠ABC,∠ACB,交点为O,则∠BOC=_________°.
120
拿出准备好的锐角三角形、钝角三角形和直角三角形纸片各一个,来动手做一做.
[任务二:中线的性质]
活动1:在纸上画一个锐角三角形,并画出它的三条中线,能画出几条 它们有怎样的位置关系
三条中线,
交于一点
做一做
活动2:在纸上画一个钝角三角形和直角三角形,画一画,折一折,它们是否都有三条中线
它们有怎样的位置关系
A
C
B
A
B
C
H
H
归纳:三角形的三条中线交于一点,这个交点就是三角形的重心.
思考:如图AE是△ABC 的中线,则BE与CE有什么关系?△ABE的面积与△AEC的面积有什么关系?
AE是△ABC的中线,得到结论BE=CE=BC.
△ABE和△AEC是等底同高,所以S△ACE=S△ABE.
典题精析
例2 如图,BD是△ABC的中线,G是BD上的一点,且BG=2GD,连接AG,若△ABC的面积为6,则图中阴影部分的面积是 .
2
1.如图,AD是BC边上的中线,AB=5cm,AD=4cm,△ABD的周长是12cm,则BC=_________cm.
2.如图,AD是△ABC的中线,S△ABC=10.求S△ABD=_________.
即时测评
6
5
即时测评
3.如图,AD是△ABC的边BC的中线,已知AB=5cm,AC=3cm,求△ABD和△ACD的周长之差.
即时测评
解:∵AD是△ABC中BC边上的中线,AB=5cm,AC=3cm,
∴BD=DC=BC,
∴△ABD和△ADC的周长的差
=(AB+BC+AD)﹣(AC+BC+AD)
=AB﹣AC
=5﹣3
=2(cm).
1.三角形一边上的中线把原三角形分成两个( )
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形
2.在△ABC中,AB=18,BC=16,BD是AC边上的中线,若△ABD的周长为41,那么△BCD的周长是( )
A.39 B.41 C.43 D.无法确定
B
A
3.已知:如图所示,在△ABC中,点D,E,F分别为BC,AD,CE的中点,且S△ABC=4cm2,则阴影部分的面积为 cm2.
4.如图,AD是△ABC的中线,已知△ABD的周长为16cm,AB比AC长3cm,则△ACD的周长为 .
1
13
5.如图,在△ABC中,BE、CF分别是AC、AB边上的中线,△ABE的周长比△BCE的周长长2,若AE=4,BF=6.
(1)求AB,AC的长;
(2)求△ABC的周长.
(1)解:∵BE、CF分别是AC、AB边上的中线,
∴点E、F分别为AC、AB的中点.
∵BF=6,AE=4,
∴AC=2AE=2×4=8,AB=2BF=2×6=12.
(2)∵△ABE的周长比△BCE的周长长2,
∴AB+AE+BE﹣BC﹣CE﹣BE=AB﹣BC=2,
由(1)得AB=12,
∴BC=12﹣2=10,
∴△ABC的周长为:12+8+10=30.
课堂小结
三角形中几条重要线段
角平分线:平分内角且与三角形对边相交的线段.
中线:连接三角形的顶点与对边中点的线段.
高线:连接顶点 和 垂足之间的线段叫作三角形的高线。
三条中线的交点是三角形的重心
基础题:1.课后习题第3题
提高题:2.请学有余力的同学做课后习题第5题并在下节课为全班展示。
课后作业
本节课到此结束,谢谢大家!
鲁教版七年级上册数学
1 认识三角形
第4课时 三角形中的三条重要线段
学习目标
1.了解三角形的中线、高线和角平分线,了解重心的概念,会画出三角形的中线,知道三角形的三条中线交于一点(重心).
2.经历画、折等操作,得到几何直观图,观察并归纳得出数学结论,发展合情推理能力.
情境&导入
如图,用铅笔可以支起一张均匀的三角形卡片.
你知道怎样确定这个点的位置吗?
“重心”
在三角形中,连接一个顶点与它对边中点的线段,叫作这个三角形的中线(median). AE是BC边上的中线.
BD=DC
B
C
D
A
1.三角形的中线
[任务一:角形的角平分线、中线、高线的定义]
三角形的中线有什么特点?
A
B
C
E
(1)AD是△ABC中BC边上的中线.
(2)点D是BC边的中点.
(3)BD=DC或BD= BC或DC= BC
或BD=DC= BC.
想一想
三角形的一个顶点向它的对边所在直线,顶点和垂足之间的线段叫作三角形的高线。
B
C
D
A
2.三角形的高线
三角形的高线有什么特点?
(1)AD是△ABC中BC边上的高线.
(2)∴∠AFB=∠CFB= 90 °.
想一想
三角形中,一个内角的角平分线和这个角的对边相交,这个角的__________点与__________点之间的线段叫作三角形的角平分线.
B
C
D
A
3.三角形的角平分线
顶点
交点
三角形的角平分线有什么特点?
(1)AD是△ABC中BC边上的角平分线.
(2)∠BAD=∠DAC或∠BAD= ∠BAC
或∠DAC= ∠BAC
或∠BAD=∠DAC= ∠BAC.
想一想
典题精析
例1.如图,在△ABC中,AD平分∠BAC且与BC相交于点D,∠B=40°,∠BAD=30°,则∠C的度数是多少?
解:∵AD平分∠BAC,
∴∠BAC=2∠BAD=2×30°=60°,
∴∠B+∠BAC+∠C=180°,
∴∠C=180°﹣∠B﹣∠BAC=180°﹣40°﹣60°=80°.
答:∠C的度数为80°
即时测评
1.如图,D,E分别为△ABC的边AC,BC的中点,则下列说法中不正确的是( )
A.DE是△BDC的中线 B.∠C的对边只有DE
C.BD是△ABC的中线 D.AD=DC,BE=EC
B
即时测评
2.如图,在△ABC中,∠A=60°,BO,CO平分∠ABC,∠ACB,交点为O,则∠BOC=_________°.
120
拿出准备好的锐角三角形、钝角三角形和直角三角形纸片各一个,来动手做一做.
[任务二:中线的性质]
活动1:在纸上画一个锐角三角形,并画出它的三条中线,能画出几条 它们有怎样的位置关系
三条中线,
交于一点
做一做
活动2:在纸上画一个钝角三角形和直角三角形,画一画,折一折,它们是否都有三条中线
它们有怎样的位置关系
A
C
B
A
B
C
H
H
归纳:三角形的三条中线交于一点,这个交点就是三角形的重心.
思考:如图AE是△ABC 的中线,则BE与CE有什么关系?△ABE的面积与△AEC的面积有什么关系?
AE是△ABC的中线,得到结论BE=CE=BC.
△ABE和△AEC是等底同高,所以S△ACE=S△ABE.
典题精析
例2 如图,BD是△ABC的中线,G是BD上的一点,且BG=2GD,连接AG,若△ABC的面积为6,则图中阴影部分的面积是 .
2
1.如图,AD是BC边上的中线,AB=5cm,AD=4cm,△ABD的周长是12cm,则BC=_________cm.
2.如图,AD是△ABC的中线,S△ABC=10.求S△ABD=_________.
即时测评
6
5
即时测评
3.如图,AD是△ABC的边BC的中线,已知AB=5cm,AC=3cm,求△ABD和△ACD的周长之差.
即时测评
解:∵AD是△ABC中BC边上的中线,AB=5cm,AC=3cm,
∴BD=DC=BC,
∴△ABD和△ADC的周长的差
=(AB+BC+AD)﹣(AC+BC+AD)
=AB﹣AC
=5﹣3
=2(cm).
1.三角形一边上的中线把原三角形分成两个( )
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形
2.在△ABC中,AB=18,BC=16,BD是AC边上的中线,若△ABD的周长为41,那么△BCD的周长是( )
A.39 B.41 C.43 D.无法确定
B
A
3.已知:如图所示,在△ABC中,点D,E,F分别为BC,AD,CE的中点,且S△ABC=4cm2,则阴影部分的面积为 cm2.
4.如图,AD是△ABC的中线,已知△ABD的周长为16cm,AB比AC长3cm,则△ACD的周长为 .
1
13
5.如图,在△ABC中,BE、CF分别是AC、AB边上的中线,△ABE的周长比△BCE的周长长2,若AE=4,BF=6.
(1)求AB,AC的长;
(2)求△ABC的周长.
(1)解:∵BE、CF分别是AC、AB边上的中线,
∴点E、F分别为AC、AB的中点.
∵BF=6,AE=4,
∴AC=2AE=2×4=8,AB=2BF=2×6=12.
(2)∵△ABE的周长比△BCE的周长长2,
∴AB+AE+BE﹣BC﹣CE﹣BE=AB﹣BC=2,
由(1)得AB=12,
∴BC=12﹣2=10,
∴△ABC的周长为:12+8+10=30.
课堂小结
三角形中几条重要线段
角平分线:平分内角且与三角形对边相交的线段.
中线:连接三角形的顶点与对边中点的线段.
高线:连接顶点 和 垂足之间的线段叫作三角形的高线。
三条中线的交点是三角形的重心
基础题:1.课后习题第3题
提高题:2.请学有余力的同学做课后习题第5题并在下节课为全班展示。
课后作业
本节课到此结束,谢谢大家!
