1.1 认识三角形 第5课时 三角形中的角平分线和高相关计算 课件(共32张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 1.1 认识三角形 第5课时 三角形中的角平分线和高相关计算 课件(共32张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 990.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 08:01:19 | ||
图片预览





文档简介
(共32张PPT)
第5课时 三角形中的角平分线和高相关计算
1 认识三角形
鲁教版七年级上册数学
1.知道三角形的三条角平分线交于一点.
2.了解三角形的高线并能在三角形中作出它,知道三角形的三条高交于一点.
3.会根据高的交点位置判断三角形的形状.
4.根据三角形的角平分线和高线进行相关的计算.
学习目标
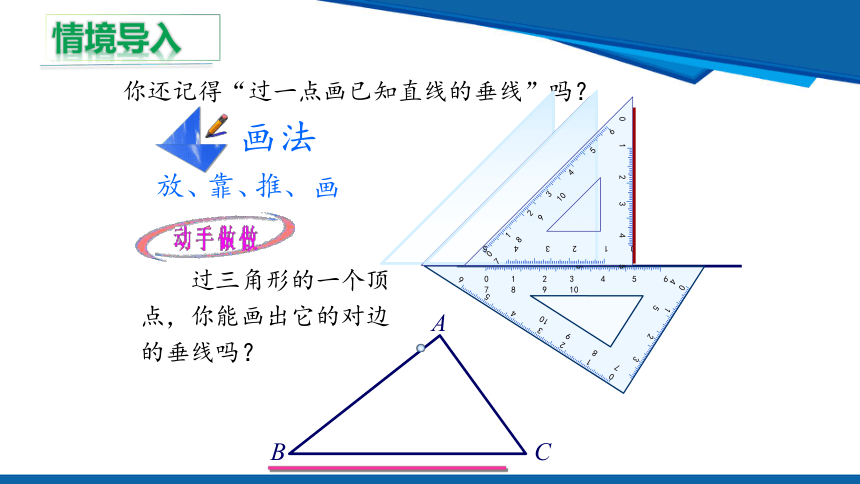
你还记得“过一点画已知直线的垂线”吗?
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
画法
放、
靠、
推、
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
画
过三角形的一个顶点,你能画出它的对边的垂线吗?
B
A
C
情境导入
(1)你能分别画出这三个三角形的三条角平分线吗?
(2)你能通过折纸的方法得到它吗
【任务一 探究三角形角平分线的性质】
B
A
C
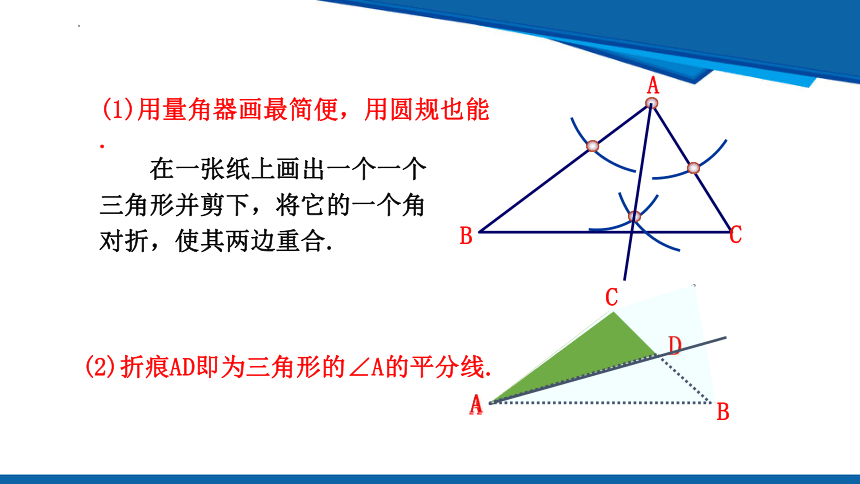
(1)用量角器画最简便,用圆规也能.
在一张纸上画出一个一个三角形并剪下,将它的一个角对折,使其两边重合.
(2)折痕AD即为三角形的∠A的平分线.
A
B
C
A
D
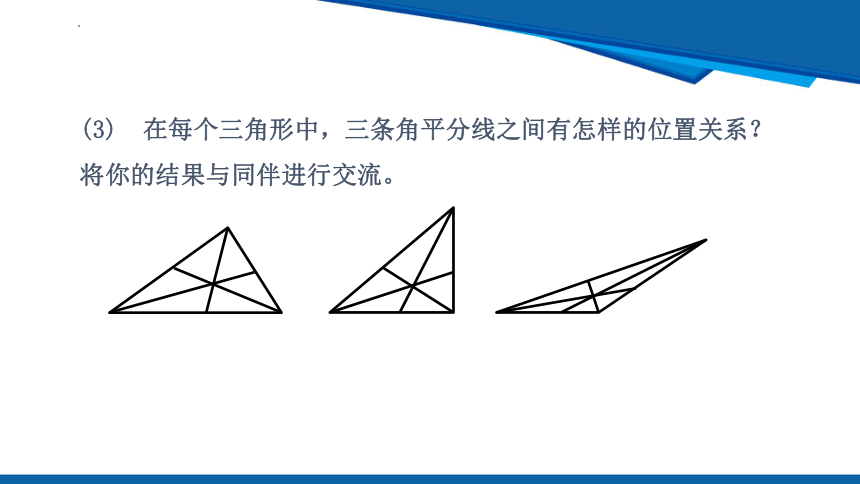
(3) 在每个三角形中,三条角平分线之间有怎样的位置关系?将你的结果与同伴进行交流。
典例精析
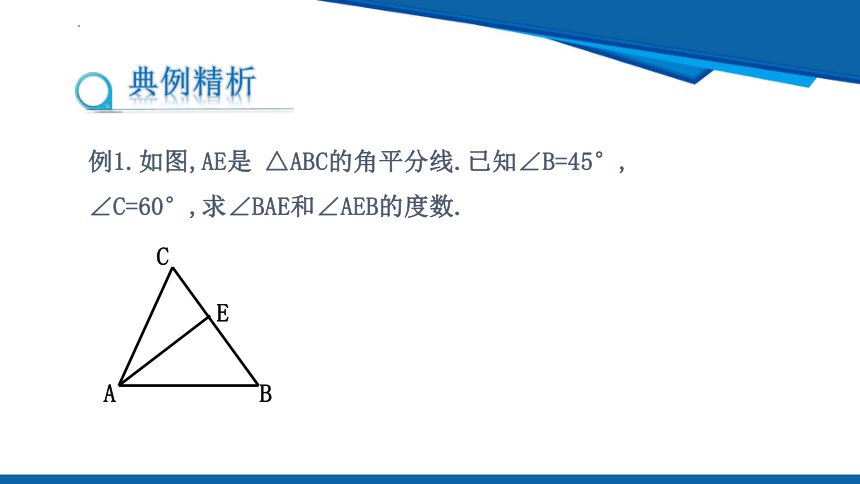
例1.如图,AE是 △ABC的角平分线.已知∠B=45°,
∠C=60°,求∠BAE和∠AEB的度数.
A
B
C
E
解:因为AE是△ABC的角平分线,
因为 ∠BAC+∠B+∠C=180°,
所以∠BAC=180°-∠B-∠C=180°-45°-60°=75°,所以∠BAE=37.5°.
因为∠AEB=∠CAE+∠C,∠CAE=∠BAE=37.5°,
所以∠AEB=37.5°+60°=97.5°.
所以∠CAE=∠BAE= ∠BAC.
D
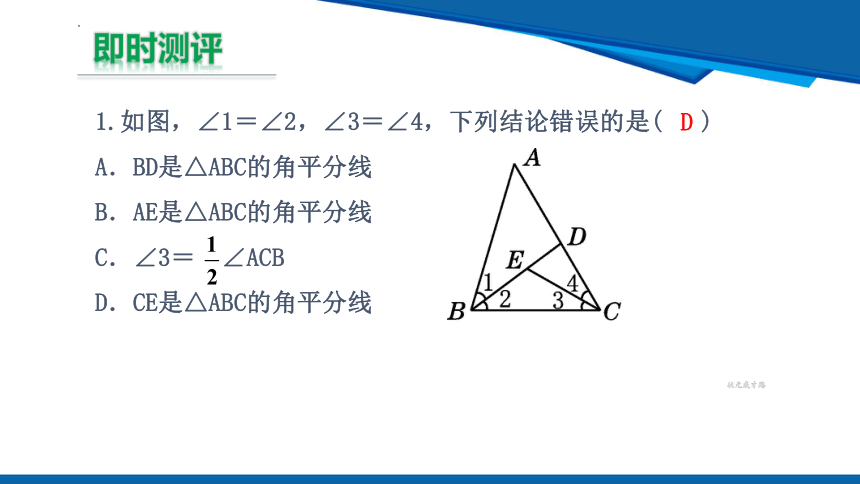
1.如图,∠1=∠2,∠3=∠4,下列结论错误的是( )
A.BD是△ABC的角平分线
B.AE是△ABC的角平分线
C.∠3= ∠ACB
D.CE是△ABC的角平分线
即时测评
2.如图,在△ABC 中,∠A = 50°,∠C = 72°,BD 是△ABC 的一条角平分线,求∠ABD 的度数.
A
B
C
D
解:因为三角形的内角和为180°.
所以∠ABC=180°-∠A-∠C=58°.
又因为BD是△ABC 的角平分线.
所以∠ABD = ∠ABC =29°.
锐角三角形的三条高
(1)准备一个锐角三角形纸片,折出或画出它的三条高,它们是否也相交于一点
锐角三角形的三条高交于同一点。
O
锐角三角形的三条高是
在三角形的内部还是外部?
使折痕过顶点,顶点的对边边缘重合。
锐角三角形的三条高都在三角形的内部。
任务二 探究高线的性质
在纸上画出一个直角三角形。
将你的结果与同伴进行交流。
A
B
C
(1)出直角三角形的三条高,
直角边BC边上的高是 ;
AB边
直角边AB边上的高是 ;
BC边
它们有怎样的位置关系?
直角三角形的三条高交于直角顶点。
D
直角三角形三条高
钝角三角形的三条高
在纸上画出一个钝角三角形。
(2) 你能折出钝角三角形的
三条高吗?
需要把CB延长。
A
C
B
B
A
A
A
A
B
C
D
F
为了便于画出AB边上的高,
需要把AB延长。
C
C
A
B
C
D
F
C
A
B
C
D
F
E
为了便于画出BC边上的高,
你能画出钝角三角形的三条高吗?
A
B
C
BC边上的高是在三角形的内部还是外部?
外部
D
AB边上的高呢?
E
F
A
B
C
D
E
F
A
B
C
D
F
(3) 钝角三角形的三条高交于一点吗?
钝角三角形的三条高不相交于一点
它们所在的直线交于一点吗?
将你的结果与同伴进行交流。
钝角三角形的三条高所在直线交于一点
O
E
归纳
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
1
1
相交
相交
不相交
相交
相交
相交
三角形的三条高所在直线交于一点
三条高所在直线的
交点的位置
三角形内部
直角顶点
三角形外部
3
典例精析
例2.如图,画△ABC的一边上的高,下列画法正确的是( )
C
2. 如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
3.三角形的三条高相交于一点,此一点定在( )
A. 三角形的内部 B.三角形的外部
C.三角形的一条边上 D. 不能确定
1.下列各组图形中,哪一组图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
D
B
D
即时测评
4.如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
即时测评
4.解:∵AD是BC边上的高,∠EAD=5°,
∴∠AED=85°.
∴∠AEB=95°.
∵∠B=50°,
∴∠BAE=180°﹣∠AEB﹣∠B=180°﹣95°﹣50°=35°,
∵AE是∠BAC的角平分线,
∴∠BAC=2∠BAE=70°,
∴∠C=180°﹣∠B﹣∠BAC=180°﹣50°﹣70°=60°.
即时测评
1.画△ABC中AB边上的高,下列画法中正确的是( )
A. B. C. D.
2.如图,△ABC中,AD⊥BC于D,点E在CD上,则图中以AD为高的三角形有 个.
C
6
3.在△ABC中,∠A+∠B=∠C,则△ABC的三条高线所在直线的交点在 .
4.如图,△ABC中,AD、AE分别为角平分线和高,∠B=46°,∠C=64°,则∠DAE= .
C
7.5
5.画出图中三角形的三条高.
解:
6.如图,在△ABC中,BE是角平分线,点D在边AB上(不与点A,B重合),CD与BE交于点O.
(1)若CD是中线,BC=3,AC=2,则△BCD与△ACD的周长差为 ;
(2)若∠ABC=62°,CD是高,求∠BOC的度数;
(3)若∠A=78°,CD是角平分线,
求∠BOC的度数.
1
6.解:(2)CD是△ABC的高,
∴∠CDB=90°,
∵∠ABC=62°,BE是△ABC的角平分线,
∴∠ABE=1/2∠ABC=1/2×62°=31°,
∴∠BOD=59°.
∴∠BOC=180°﹣59°=121°.
6.解:(3)∵∠A=78°,
∴∠ABC+∠ACB=180°﹣∠A
=180°﹣78°=102°,
∵BE,CD是△ABC的角平分线,
∴∠OBC=1/2∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)
=×102°=51°,
∴∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣51°=129°.
课堂小结
锐角三角形 直角三角形 钝角三角形
三条高都在三角形内部 一条高在三角形内部,两条高在直角边上 一条高在三角形内部,两条高在三角形外部
2.三角形的三条高的特性
任意三角形的三条高所在的直线交于一点.
任意三角形的三条角平分线的交点都在三角形的内部.
1.三角形的三条角平分线特征
基础题:1.课后习题第 1题
提高题:2.请学有余力的同学做课后习题第4题并在全班内展示、讲解。
课后作业
本节课到此结束,谢谢大家!
第5课时 三角形中的角平分线和高相关计算
1 认识三角形
鲁教版七年级上册数学
1.知道三角形的三条角平分线交于一点.
2.了解三角形的高线并能在三角形中作出它,知道三角形的三条高交于一点.
3.会根据高的交点位置判断三角形的形状.
4.根据三角形的角平分线和高线进行相关的计算.
学习目标
你还记得“过一点画已知直线的垂线”吗?
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
画法
放、
靠、
推、
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
画
过三角形的一个顶点,你能画出它的对边的垂线吗?
B
A
C
情境导入
(1)你能分别画出这三个三角形的三条角平分线吗?
(2)你能通过折纸的方法得到它吗
【任务一 探究三角形角平分线的性质】
B
A
C
(1)用量角器画最简便,用圆规也能.
在一张纸上画出一个一个三角形并剪下,将它的一个角对折,使其两边重合.
(2)折痕AD即为三角形的∠A的平分线.
A
B
C
A
D
(3) 在每个三角形中,三条角平分线之间有怎样的位置关系?将你的结果与同伴进行交流。
典例精析
例1.如图,AE是 △ABC的角平分线.已知∠B=45°,
∠C=60°,求∠BAE和∠AEB的度数.
A
B
C
E
解:因为AE是△ABC的角平分线,
因为 ∠BAC+∠B+∠C=180°,
所以∠BAC=180°-∠B-∠C=180°-45°-60°=75°,所以∠BAE=37.5°.
因为∠AEB=∠CAE+∠C,∠CAE=∠BAE=37.5°,
所以∠AEB=37.5°+60°=97.5°.
所以∠CAE=∠BAE= ∠BAC.
D
1.如图,∠1=∠2,∠3=∠4,下列结论错误的是( )
A.BD是△ABC的角平分线
B.AE是△ABC的角平分线
C.∠3= ∠ACB
D.CE是△ABC的角平分线
即时测评
2.如图,在△ABC 中,∠A = 50°,∠C = 72°,BD 是△ABC 的一条角平分线,求∠ABD 的度数.
A
B
C
D
解:因为三角形的内角和为180°.
所以∠ABC=180°-∠A-∠C=58°.
又因为BD是△ABC 的角平分线.
所以∠ABD = ∠ABC =29°.
锐角三角形的三条高
(1)准备一个锐角三角形纸片,折出或画出它的三条高,它们是否也相交于一点
锐角三角形的三条高交于同一点。
O
锐角三角形的三条高是
在三角形的内部还是外部?
使折痕过顶点,顶点的对边边缘重合。
锐角三角形的三条高都在三角形的内部。
任务二 探究高线的性质
在纸上画出一个直角三角形。
将你的结果与同伴进行交流。
A
B
C
(1)出直角三角形的三条高,
直角边BC边上的高是 ;
AB边
直角边AB边上的高是 ;
BC边
它们有怎样的位置关系?
直角三角形的三条高交于直角顶点。
D
直角三角形三条高
钝角三角形的三条高
在纸上画出一个钝角三角形。
(2) 你能折出钝角三角形的
三条高吗?
需要把CB延长。
A
C
B
B
A
A
A
A
B
C
D
F
为了便于画出AB边上的高,
需要把AB延长。
C
C
A
B
C
D
F
C
A
B
C
D
F
E
为了便于画出BC边上的高,
你能画出钝角三角形的三条高吗?
A
B
C
BC边上的高是在三角形的内部还是外部?
外部
D
AB边上的高呢?
E
F
A
B
C
D
E
F
A
B
C
D
F
(3) 钝角三角形的三条高交于一点吗?
钝角三角形的三条高不相交于一点
它们所在的直线交于一点吗?
将你的结果与同伴进行交流。
钝角三角形的三条高所在直线交于一点
O
E
归纳
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
1
1
相交
相交
不相交
相交
相交
相交
三角形的三条高所在直线交于一点
三条高所在直线的
交点的位置
三角形内部
直角顶点
三角形外部
3
典例精析
例2.如图,画△ABC的一边上的高,下列画法正确的是( )
C
2. 如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
3.三角形的三条高相交于一点,此一点定在( )
A. 三角形的内部 B.三角形的外部
C.三角形的一条边上 D. 不能确定
1.下列各组图形中,哪一组图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
D
B
D
即时测评
4.如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
即时测评
4.解:∵AD是BC边上的高,∠EAD=5°,
∴∠AED=85°.
∴∠AEB=95°.
∵∠B=50°,
∴∠BAE=180°﹣∠AEB﹣∠B=180°﹣95°﹣50°=35°,
∵AE是∠BAC的角平分线,
∴∠BAC=2∠BAE=70°,
∴∠C=180°﹣∠B﹣∠BAC=180°﹣50°﹣70°=60°.
即时测评
1.画△ABC中AB边上的高,下列画法中正确的是( )
A. B. C. D.
2.如图,△ABC中,AD⊥BC于D,点E在CD上,则图中以AD为高的三角形有 个.
C
6
3.在△ABC中,∠A+∠B=∠C,则△ABC的三条高线所在直线的交点在 .
4.如图,△ABC中,AD、AE分别为角平分线和高,∠B=46°,∠C=64°,则∠DAE= .
C
7.5
5.画出图中三角形的三条高.
解:
6.如图,在△ABC中,BE是角平分线,点D在边AB上(不与点A,B重合),CD与BE交于点O.
(1)若CD是中线,BC=3,AC=2,则△BCD与△ACD的周长差为 ;
(2)若∠ABC=62°,CD是高,求∠BOC的度数;
(3)若∠A=78°,CD是角平分线,
求∠BOC的度数.
1
6.解:(2)CD是△ABC的高,
∴∠CDB=90°,
∵∠ABC=62°,BE是△ABC的角平分线,
∴∠ABE=1/2∠ABC=1/2×62°=31°,
∴∠BOD=59°.
∴∠BOC=180°﹣59°=121°.
6.解:(3)∵∠A=78°,
∴∠ABC+∠ACB=180°﹣∠A
=180°﹣78°=102°,
∵BE,CD是△ABC的角平分线,
∴∠OBC=1/2∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)
=×102°=51°,
∴∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣51°=129°.
课堂小结
锐角三角形 直角三角形 钝角三角形
三条高都在三角形内部 一条高在三角形内部,两条高在直角边上 一条高在三角形内部,两条高在三角形外部
2.三角形的三条高的特性
任意三角形的三条高所在的直线交于一点.
任意三角形的三条角平分线的交点都在三角形的内部.
1.三角形的三条角平分线特征
基础题:1.课后习题第 1题
提高题:2.请学有余力的同学做课后习题第4题并在全班内展示、讲解。
课后作业
本节课到此结束,谢谢大家!
