1.3 探索全等三角形的条件 第2课时 角边角或角角边 课件(共31张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 1.3 探索全等三角形的条件 第2课时 角边角或角角边 课件(共31张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 911.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 08:03:32 | ||
图片预览







文档简介
(共31张PPT)
鲁教版七年级上册数学
第一章 三角形
3 探索全等三角形的条件
第2课时 角边角或角角边
学习目标
1.经历探索判定三角形全等“角边角”“角角边”条件的过程;
2.掌握并能应用“角边角” “角角边”条件证明两个三角形全等.
3.能用尺规作图:两角及其夹边作三角形.
如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适
你能说明其中理由吗
3
2
1
判定两个三角形全等的基本事实:“角边角”
我们知道:如果给出一个三角形三条边的长度,那么因此得到的三角形都是全等.
如果已知一个三角形的两角及一边,那么有几种可能的情况呢
[任务一 探究三角形全等的判定“ASA”]”
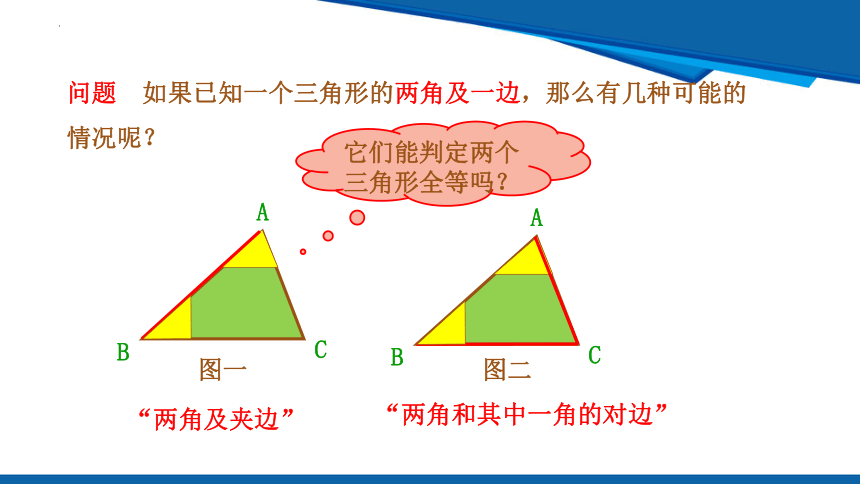
问题 如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
A
B
C
A
B
C
图一
图二
“两角及夹边”
“两角和其中一角的对边”
它们能判定两个三角形全等吗?
问题1
如果“两角及一边”条件中的边是两角所夹的边,比如三角形的两个内角分别是α和β,它们所夹的边为 a cm,你能画出这个三角形吗?
α
β
a cm
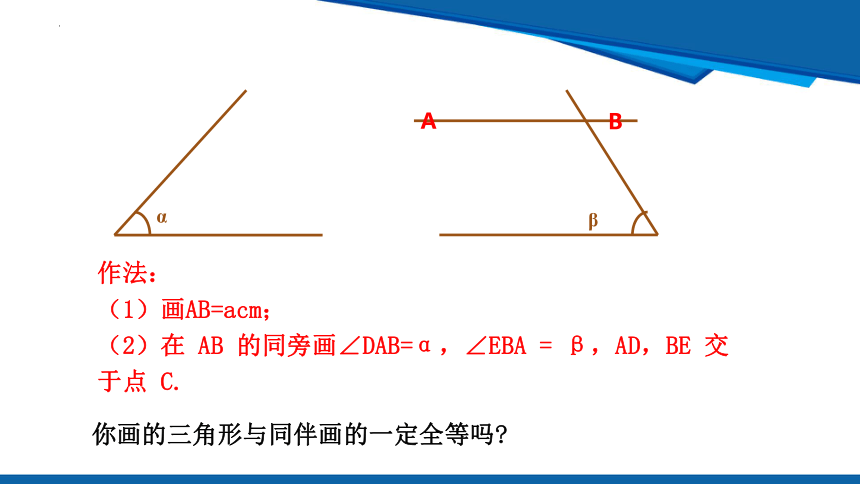
你画的三角形与同伴画的一定全等吗
作法:
(1)画AB=acm;
(2)在 AB 的同旁画∠DAB=α,∠EBA = β,AD,BE 交于点 C.
α
β
A
B
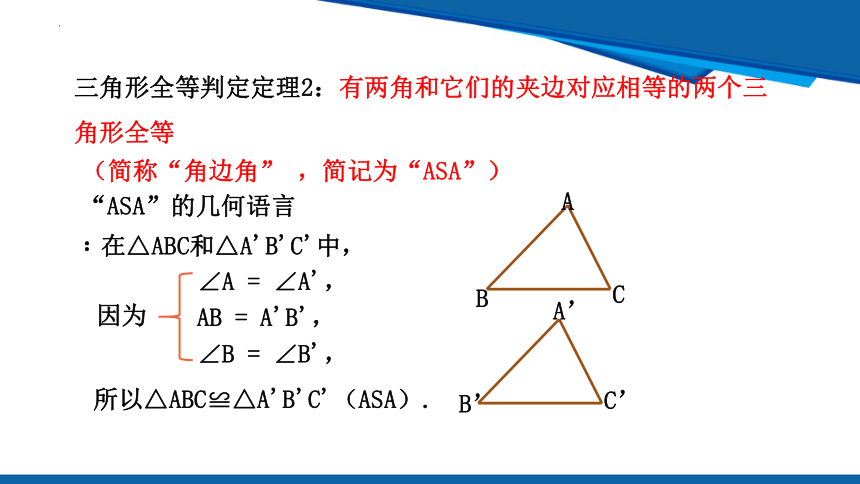
三角形全等判定定理2:有两角和它们的夹边对应相等的两个三角形全等
(简称“角边角” ,简记为“ASA”)
A
C
B
A’
C’
B’
“ASA”的几何语言:
在△ABC和△A'B'C'中,
因为
∠A = ∠A',
AB = A'B',
∠B = ∠B',
所以△ABC≌△A'B'C'(ASA).
典例精析
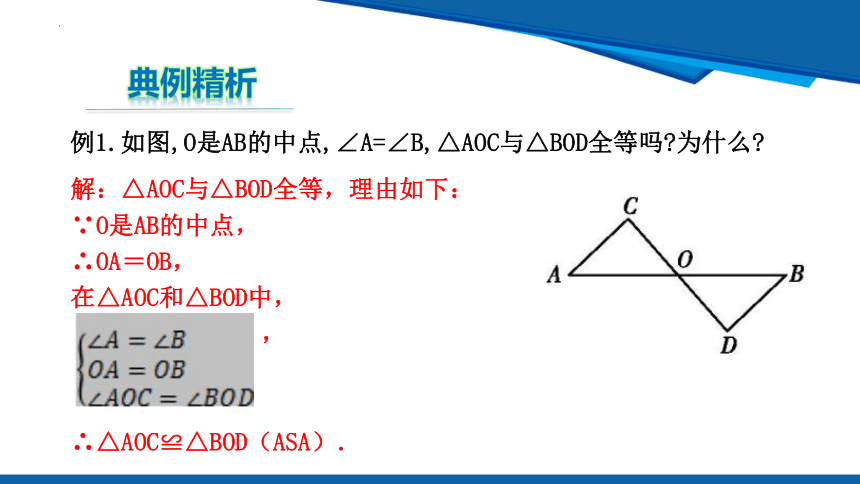
例1.如图,O是AB的中点,∠A=∠B,△AOC与△BOD全等吗 为什么
解:△AOC与△BOD全等,理由如下:
∵O是AB的中点,
∴OA=OB,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(ASA).
即时测评
1.如图,AC和BD交于点E,∠B=∠D,BE=DE,ΔABE与ΔCDE全等吗?为什么?
解:在△ABE和△DCE中,
∠B=∠D(已知 ),
BE=DE(已知),
∠AEB=∠DEC (对顶角 ),
所以 △ABE≌△CDE(ASA),
即时测评
2.如图,点D在AB上,点E在AC上,AB=AC, ∠B=∠C,试说明:AD=AE.
A
B
C
D
E
解:在△ACD和△ABE中,
∠A=∠A(公共角 ),
AC=AB(已知),
∠C=∠B (已知 ),
所以 △ACD≌△ABE(ASA),
所以AD=AE.
例2.已知三角形的两角及其夹边,求作这个三角形.
已知:线段 c,∠α ,∠β.
β
c
α
求作△ABC,∠A =∠α ,∠B =∠β,AB = c.
[任务二 探究“ASA”尺规作图]
作法:
(1)作∠DAF=∠α.
(2)在射线AF上截取线段AB=c;
(3)以B为顶点,以BA为一边,作∠ABE=∠β,BE交AD于点C,连接BC.则△ABC就是所求作的三角形.
A
F
D
B
A
D
F
C
A
B
D
F
E
即时测评
1.已知∠α和线段a,用尺规作一个三角形,使其一个内角等于∠α,另一个内角等于2∠α,且这两内角的夹边等于a.
解:如图,
三角形ABC即为所求.
如果“两角及一边”条件中的边是其中一角的对边,情况会怎样呢?
若三角形的两个内角分别是α和β,且70°所对的边为 acm,你能画出这个三角形吗
α
β
a cm
任务三 探究三角形全等的判定“AAS”]
α
β
a cm
A
B
根据三角形的内角和为180°,所以第三个角度数为 180°-α-β.
D
α
E
180°-α-β
C
β
两角分别相等且其中一组对角的对边相等的两个三角形全等.简写成“角角边”或“AAS”.
∠A=∠A′(已知),
∠B=∠B′ (已知),
AC=A′C ′(已知),
在△ABC和△A′B′C′中,
所以 △ABC≌△ A′B′C′(AAS).
A
B
C
A′
B′
C′
典例精析
例3.如图,AB∥DE,AC∥DF,AC=DF,∠B=∠E.求证:△ABC≌△DEF.
证明:∵AB∥DE,AC∥DF,
∴∠D=∠DOC,∠A=∠DOC,
∴∠A=∠D,
在△ABC与△DEF中,
∴△ABC≌△DEF(AAS).
∠A = ∠D,
AC = DF,
∠B = ∠E,
即时测评
1.如图,已知BD=CE,∠B=∠C,△ABD与△ACE全等吗?为什么?
解:在△ABD和△ACE中,
∠A = ∠A,
BD = CE,
∠B = ∠C,
所以△ABD ≌ △ACE(AAS)
即时测评
2.如图,点 A,B,C,D 在同一条直线上,BE//DF,∠A=∠F,BE=CD. 试说明:AE=FC.
解:因为BE // DF,
所以∠ABE = ∠D,
在△ABE 和 △FDC 中,
∠ABE = ∠D,
BE = CD,
∠A = ∠F,
所以△ABE ≌ △FDC(AAS)
所以AE = FC .
F
A
C
B
D
E
1.根据下列条件,能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠D B.∠B=∠E,∠A=∠D,AC=EF
C.∠A=∠D,∠C=∠F,AC=EF D.AB=DE,BC=EF,∠B=∠E
2.如图,A、B、C、D在同一直线上,AE∥DF,AE=DF,
添加一个条件,不能判定△AEC≌△DFB的是( )
A.EC∥BF B.EC=BF C.AB=CD D.∠E=∠F
D
B
3.如图,在△ABC中,AB=AC,AD⊥BC于点D,CE⊥AB于点E,AE=CE,AD与CE相交于点F.试说明:△AEF≌△CEB.
3.证明 : 因为AD⊥BC,
所以 ∠B+∠BAD=90°,
因为 CE⊥AB,
所以 ∠AEF=∠CEB=90°,
所以 ∠B+∠BCE=90°,
所以 ∠EAF=∠ECB,
在△AEF和△CEB中,
所以△AEF≌△CEB(SAS)
4.如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.
(1)试说明:△ABD≌△EDC;
(2)若AB=2,BE=3,求CD的长.
解:(1)△ABD≌△EDC;
∵ 在△ABD和△EDC中,
∴△ABD≌△EDC(AAS).
(2)因为△ABD≌△EDC,
所以DE=AB=2,CD=BD,
所以CD=BD=DE+BE=2+3=5.
5.如图,已知△ABC中,BE⊥AD于E,CF⊥AD于F,且BE=CF,那么BD与CD相等吗?
解:BD=CD.
理由:∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°.
在△BED和△CFD中,
∴△BED≌△CFD(AAS),
∴BD=CD.
基础题:1.课后习题第 1题
提高题:2.请学有余力的同学课后习题第 4题,,下节课在全班展示、交流。
课后作业
本节课到此结束,谢谢大家!
鲁教版七年级上册数学
第一章 三角形
3 探索全等三角形的条件
第2课时 角边角或角角边
学习目标
1.经历探索判定三角形全等“角边角”“角角边”条件的过程;
2.掌握并能应用“角边角” “角角边”条件证明两个三角形全等.
3.能用尺规作图:两角及其夹边作三角形.
如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适
你能说明其中理由吗
3
2
1
判定两个三角形全等的基本事实:“角边角”
我们知道:如果给出一个三角形三条边的长度,那么因此得到的三角形都是全等.
如果已知一个三角形的两角及一边,那么有几种可能的情况呢
[任务一 探究三角形全等的判定“ASA”]”
问题 如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
A
B
C
A
B
C
图一
图二
“两角及夹边”
“两角和其中一角的对边”
它们能判定两个三角形全等吗?
问题1
如果“两角及一边”条件中的边是两角所夹的边,比如三角形的两个内角分别是α和β,它们所夹的边为 a cm,你能画出这个三角形吗?
α
β
a cm
你画的三角形与同伴画的一定全等吗
作法:
(1)画AB=acm;
(2)在 AB 的同旁画∠DAB=α,∠EBA = β,AD,BE 交于点 C.
α
β
A
B
三角形全等判定定理2:有两角和它们的夹边对应相等的两个三角形全等
(简称“角边角” ,简记为“ASA”)
A
C
B
A’
C’
B’
“ASA”的几何语言:
在△ABC和△A'B'C'中,
因为
∠A = ∠A',
AB = A'B',
∠B = ∠B',
所以△ABC≌△A'B'C'(ASA).
典例精析
例1.如图,O是AB的中点,∠A=∠B,△AOC与△BOD全等吗 为什么
解:△AOC与△BOD全等,理由如下:
∵O是AB的中点,
∴OA=OB,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(ASA).
即时测评
1.如图,AC和BD交于点E,∠B=∠D,BE=DE,ΔABE与ΔCDE全等吗?为什么?
解:在△ABE和△DCE中,
∠B=∠D(已知 ),
BE=DE(已知),
∠AEB=∠DEC (对顶角 ),
所以 △ABE≌△CDE(ASA),
即时测评
2.如图,点D在AB上,点E在AC上,AB=AC, ∠B=∠C,试说明:AD=AE.
A
B
C
D
E
解:在△ACD和△ABE中,
∠A=∠A(公共角 ),
AC=AB(已知),
∠C=∠B (已知 ),
所以 △ACD≌△ABE(ASA),
所以AD=AE.
例2.已知三角形的两角及其夹边,求作这个三角形.
已知:线段 c,∠α ,∠β.
β
c
α
求作△ABC,∠A =∠α ,∠B =∠β,AB = c.
[任务二 探究“ASA”尺规作图]
作法:
(1)作∠DAF=∠α.
(2)在射线AF上截取线段AB=c;
(3)以B为顶点,以BA为一边,作∠ABE=∠β,BE交AD于点C,连接BC.则△ABC就是所求作的三角形.
A
F
D
B
A
D
F
C
A
B
D
F
E
即时测评
1.已知∠α和线段a,用尺规作一个三角形,使其一个内角等于∠α,另一个内角等于2∠α,且这两内角的夹边等于a.
解:如图,
三角形ABC即为所求.
如果“两角及一边”条件中的边是其中一角的对边,情况会怎样呢?
若三角形的两个内角分别是α和β,且70°所对的边为 acm,你能画出这个三角形吗
α
β
a cm
任务三 探究三角形全等的判定“AAS”]
α
β
a cm
A
B
根据三角形的内角和为180°,所以第三个角度数为 180°-α-β.
D
α
E
180°-α-β
C
β
两角分别相等且其中一组对角的对边相等的两个三角形全等.简写成“角角边”或“AAS”.
∠A=∠A′(已知),
∠B=∠B′ (已知),
AC=A′C ′(已知),
在△ABC和△A′B′C′中,
所以 △ABC≌△ A′B′C′(AAS).
A
B
C
A′
B′
C′
典例精析
例3.如图,AB∥DE,AC∥DF,AC=DF,∠B=∠E.求证:△ABC≌△DEF.
证明:∵AB∥DE,AC∥DF,
∴∠D=∠DOC,∠A=∠DOC,
∴∠A=∠D,
在△ABC与△DEF中,
∴△ABC≌△DEF(AAS).
∠A = ∠D,
AC = DF,
∠B = ∠E,
即时测评
1.如图,已知BD=CE,∠B=∠C,△ABD与△ACE全等吗?为什么?
解:在△ABD和△ACE中,
∠A = ∠A,
BD = CE,
∠B = ∠C,
所以△ABD ≌ △ACE(AAS)
即时测评
2.如图,点 A,B,C,D 在同一条直线上,BE//DF,∠A=∠F,BE=CD. 试说明:AE=FC.
解:因为BE // DF,
所以∠ABE = ∠D,
在△ABE 和 △FDC 中,
∠ABE = ∠D,
BE = CD,
∠A = ∠F,
所以△ABE ≌ △FDC(AAS)
所以AE = FC .
F
A
C
B
D
E
1.根据下列条件,能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠D B.∠B=∠E,∠A=∠D,AC=EF
C.∠A=∠D,∠C=∠F,AC=EF D.AB=DE,BC=EF,∠B=∠E
2.如图,A、B、C、D在同一直线上,AE∥DF,AE=DF,
添加一个条件,不能判定△AEC≌△DFB的是( )
A.EC∥BF B.EC=BF C.AB=CD D.∠E=∠F
D
B
3.如图,在△ABC中,AB=AC,AD⊥BC于点D,CE⊥AB于点E,AE=CE,AD与CE相交于点F.试说明:△AEF≌△CEB.
3.证明 : 因为AD⊥BC,
所以 ∠B+∠BAD=90°,
因为 CE⊥AB,
所以 ∠AEF=∠CEB=90°,
所以 ∠B+∠BCE=90°,
所以 ∠EAF=∠ECB,
在△AEF和△CEB中,
所以△AEF≌△CEB(SAS)
4.如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.
(1)试说明:△ABD≌△EDC;
(2)若AB=2,BE=3,求CD的长.
解:(1)△ABD≌△EDC;
∵ 在△ABD和△EDC中,
∴△ABD≌△EDC(AAS).
(2)因为△ABD≌△EDC,
所以DE=AB=2,CD=BD,
所以CD=BD=DE+BE=2+3=5.
5.如图,已知△ABC中,BE⊥AD于E,CF⊥AD于F,且BE=CF,那么BD与CD相等吗?
解:BD=CD.
理由:∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°.
在△BED和△CFD中,
∴△BED≌△CFD(AAS),
∴BD=CD.
基础题:1.课后习题第 1题
提高题:2.请学有余力的同学课后习题第 4题,,下节课在全班展示、交流。
课后作业
本节课到此结束,谢谢大家!
