1.3 探索三角形全等的条件 第4课时 选择合适的方法判定三角形全等 课件(共29张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 1.3 探索三角形全等的条件 第4课时 选择合适的方法判定三角形全等 课件(共29张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 645.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
3 探索三角形全等的条件
第4课时 选择合适的方法判定三角形全等
鲁教版七年级上册数学
1.会根据所学的全等三角形的判定,添加适当的条件,证明三角形的全等.
2.探究全等三角形的对应“角平分线、中线、高线”之间的关系.
3.利用全等三角形的判断和性质进行相关的计算或说理.
学习目标
前面我们学习了三角形全等的判定“SSS”“SAS”“ASA”及“AAS”,那么三角形中,只给定两个条件,你如何根据三角形全等的判定选择合适的条件,使所给的三角形全等呢?
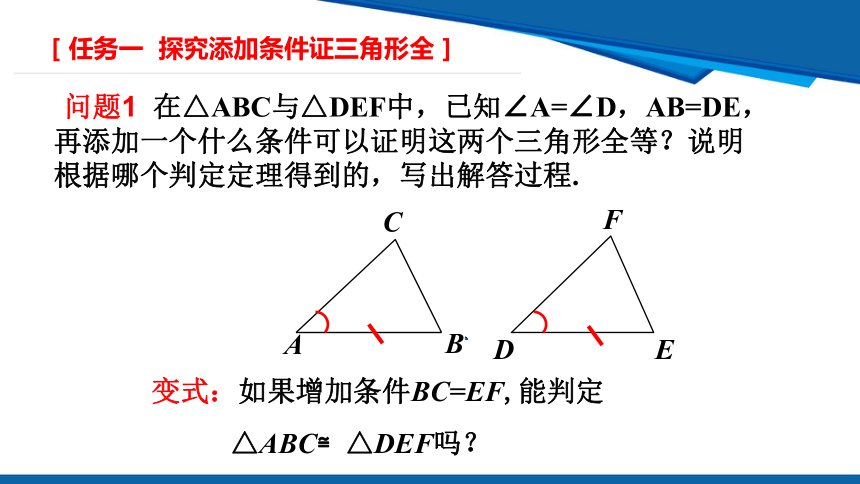
问题1 在△ABC与△DEF中,已知∠A=∠D,AB=DE,再添加一个什么条件可以证明这两个三角形全等?说明根据哪个判定定理得到的,写出解答过程.
变式:如果增加条件BC=EF,能判定
△ABC≌△DEF吗?
C
A
B
D
E
F
[任务一 探究添加条件证三角形全]
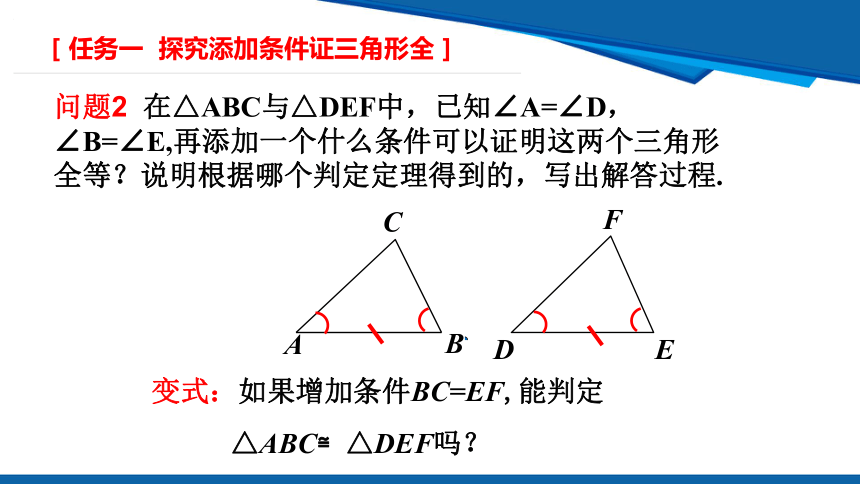
问题2 在△ABC与△DEF中,已知∠A=∠D,∠B=∠E,再添加一个什么条件可以证明这两个三角形全等?说明根据哪个判定定理得到的,写出解答过程.
变式:如果增加条件BC=EF,能判定
△ABC≌△DEF吗?
C
A
B
D
E
F
[任务一 探究添加条件证三角形全]
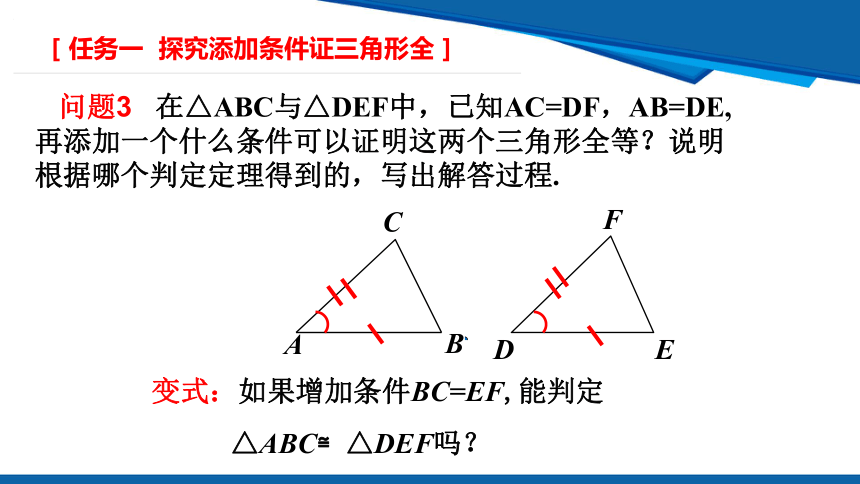
问题3 在△ABC与△DEF中,已知AC=DF,AB=DE,再添加一个什么条件可以证明这两个三角形全等?说明根据哪个判定定理得到的,写出解答过程.
变式:如果增加条件BC=EF,能判定
△ABC≌△DEF吗?
C
A
B
D
E
F
[任务一 探究添加条件证三角形全]
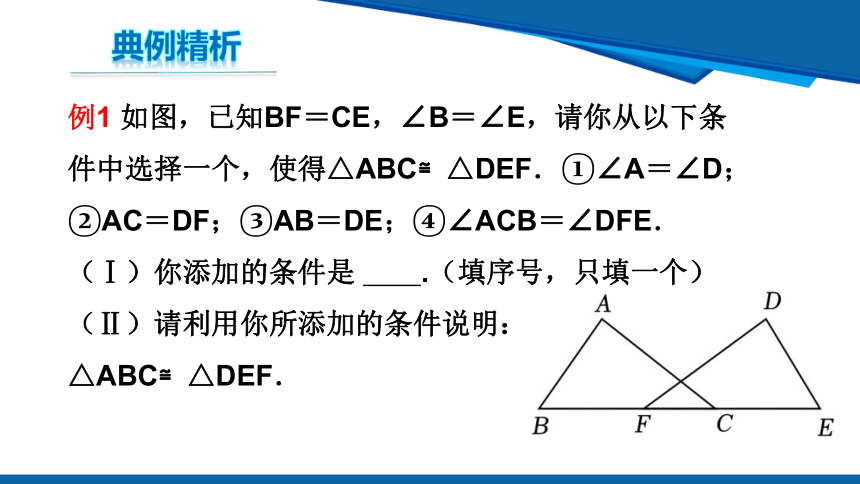
例1 如图,已知BF=CE,∠B=∠E,请你从以下条件中选择一个,使得△ABC≌△DEF.①∠A=∠D;②AC=DF;③AB=DE;④∠ACB=∠DFE.
(Ⅰ)你添加的条件是 .(填序号,只填一个)
(Ⅱ)请利用你所添加的条件说明:△ABC≌△DEF.
典例精析
例1 解:添加的条件是③(答案不唯一),
故答案为:③(答案不唯一).
(Ⅱ)证明:∵BF=CE,
∴BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS).
1.如图,AB=AC,AD=AE,欲证△ABD≌△ACE,可补充条件( )
A.∠1=∠2 B.∠B=∠C C.∠D=∠E D.∠BAE=∠CAD
即时测评
A
2.如图,AD=BC,要得到△ABD和△CDB全等,可以添加的条件是( )
A.AB∥CD B.AD∥BC
C.∠A=∠C D.∠ABC=∠CDA
即时测评
B
3.如图,M是AB的中点,MC=MD,∠1=∠2,判定△AMC≌△BMD的方法是 ;
若M是AB的中点,∠C=∠D,∠1=∠2,判定△AMC≌△BMD的方法是 ;
若M是AB的中点,∠A=∠B,∠1=∠2,判定△AMC≌△BMD的方法是 ;
即时测评
SAS
AAS
ASA
例2 如图,已知△ABC≌△A1B1C1 ,D与D1分别是BC、B1C1上的一点,且BD=B1D1.那么AD=A1D1吗?为什么?
A
B
D
C
A
1
B
1
D
1
C
1
典例精析
[任务二 探究全等三角形的对应“角平分线、中线、高线”之间的关系]
说明两个角相等、两条线段相等的基本方法:说明这两个角或两条线段所在的两个三角形全等。
答:AD=A1D1
证明: ∵△ABC≌△A1B1C1
∴ ∠B=∠B1,AB=A1B1
∵在△ABD和△A1B1D1中
AB=A1B1
∠B=∠B1
BD=B1D1
∴△ABD≌△A1B1D1 (SAS)
∴ AD=A1D1
全等三角形的对应中线、对应角平分线、对应高是否分别相等呢?
要求:先独立完成,然后小组内交流讨论,最后小组展示、点评.
A
B
D
C
A
1
B
1
D
1
C
1
类比推理
已知:如图,△ABC≌△A1B1C1 ,AD、A1D1 分别是△ABC和△A1B1C1 的中线.那么AD = A1D1吗?请说明理由.
问题1
全等三角形的对应中线相等。
问题2
已知:如图,△ABC≌△A1B1C1 ,AD、A1D1 分别是△ABC和△A1B1C1 的角平分线.那么AD = A1D1吗?请说明理由.
全等三角形的对应角平分线相等。
问题3
已知:如图, △ABC≌△A1B1C1 ,AD、 A1D1 分别是△ABC和△A1B1C1 的高. 那么AD = A1D1吗?请说明理由.
全等三角形的对应高相等。
两个全等三角形的面积是否相等 周长呢 你能说明理由吗?
结论:两个全等三角形的面积 ,周长也 .
追问
相等
相等
1.下列说法中:
⑴全等三角形的周长相等、面积相等;
⑵面积相等的两个三角形是全等三角形;
⑶全等三角形对应边上的高、中线及对应角平分线分别相等,其中正确的个数有( )
A.3个 B.2个 C.1个 D.0个
即时测评
B
1.如图,已知:∠B=∠DEF,BC=EF,现要说明△ABC≌△DEF,
(1)若要以“SAS”为依据,还缺条件 ;
(2)若要以“ASA”为依据,还缺条件 ;
(3)若要以“AAS”为依据,还缺条件 .
B
AB=DE
∠ACB=∠DFE
∠A=∠D
2.已知:如图,在△ABC中,D是边BC上一点,BE⊥AD,CF⊥AD,垂足分别为E、F.若AD是△ABC的中线,BE与CF有什么关系?并说明理由.
解:BE∥CF且BE=CF.理由如下:
∵AD是△ABC的中线,
∴BD=CD,
在△BED和△CFD中
∴△BED≌△CFD,
∴BE=CF.
∵BE⊥AD,CF⊥AD,
∴BE∥CF.
综上,BE∥CF且BE=CF.
3.如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE,试说明:△ABC≌△ADE的理由.
解:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
即∠BAC=∠DAE,
∵∠B+∠1=∠ADE+∠3,
且∠1=∠3,
∴∠B=∠ADE,
在△ABC和△ADE中
∴△ABC≌△ADE(AAS).
4.如图,已知在Rt△ABC,AB=AC,∠BAC=90°,AN是过点A的任一条直线,BD⊥AN于D,CE⊥AN于E.试说明:DE=BD﹣CE.
解:∵∠BAC=90°,
∴∠BAD+∠EAC=90°,
又∵BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
∠BAD+∠ABD=90°,
∴∠ABD=∠EAC,
又∵AB=AC,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE=AD+DE=CE+DE,
∴BD=DE+CE,
即DE=BD﹣CE.
今天这节课,我们有哪些收获?
判定三角形全等的四种方法,
会选取恰当的方法解决三角形全等问题。
2. 全等三角形的对应中线、对应高、对应角平分线分别相等。
3. 类比、转化等数学思想的应用。
课堂小结
基础题:1.课后习题第2题
提高题:2.请学有余力的同学课后习题第3、4题,下节课在全班展示、交流。
课后作业
本节课到此结束,谢谢大家!
3 探索三角形全等的条件
第4课时 选择合适的方法判定三角形全等
鲁教版七年级上册数学
1.会根据所学的全等三角形的判定,添加适当的条件,证明三角形的全等.
2.探究全等三角形的对应“角平分线、中线、高线”之间的关系.
3.利用全等三角形的判断和性质进行相关的计算或说理.
学习目标
前面我们学习了三角形全等的判定“SSS”“SAS”“ASA”及“AAS”,那么三角形中,只给定两个条件,你如何根据三角形全等的判定选择合适的条件,使所给的三角形全等呢?
问题1 在△ABC与△DEF中,已知∠A=∠D,AB=DE,再添加一个什么条件可以证明这两个三角形全等?说明根据哪个判定定理得到的,写出解答过程.
变式:如果增加条件BC=EF,能判定
△ABC≌△DEF吗?
C
A
B
D
E
F
[任务一 探究添加条件证三角形全]
问题2 在△ABC与△DEF中,已知∠A=∠D,∠B=∠E,再添加一个什么条件可以证明这两个三角形全等?说明根据哪个判定定理得到的,写出解答过程.
变式:如果增加条件BC=EF,能判定
△ABC≌△DEF吗?
C
A
B
D
E
F
[任务一 探究添加条件证三角形全]
问题3 在△ABC与△DEF中,已知AC=DF,AB=DE,再添加一个什么条件可以证明这两个三角形全等?说明根据哪个判定定理得到的,写出解答过程.
变式:如果增加条件BC=EF,能判定
△ABC≌△DEF吗?
C
A
B
D
E
F
[任务一 探究添加条件证三角形全]
例1 如图,已知BF=CE,∠B=∠E,请你从以下条件中选择一个,使得△ABC≌△DEF.①∠A=∠D;②AC=DF;③AB=DE;④∠ACB=∠DFE.
(Ⅰ)你添加的条件是 .(填序号,只填一个)
(Ⅱ)请利用你所添加的条件说明:△ABC≌△DEF.
典例精析
例1 解:添加的条件是③(答案不唯一),
故答案为:③(答案不唯一).
(Ⅱ)证明:∵BF=CE,
∴BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS).
1.如图,AB=AC,AD=AE,欲证△ABD≌△ACE,可补充条件( )
A.∠1=∠2 B.∠B=∠C C.∠D=∠E D.∠BAE=∠CAD
即时测评
A
2.如图,AD=BC,要得到△ABD和△CDB全等,可以添加的条件是( )
A.AB∥CD B.AD∥BC
C.∠A=∠C D.∠ABC=∠CDA
即时测评
B
3.如图,M是AB的中点,MC=MD,∠1=∠2,判定△AMC≌△BMD的方法是 ;
若M是AB的中点,∠C=∠D,∠1=∠2,判定△AMC≌△BMD的方法是 ;
若M是AB的中点,∠A=∠B,∠1=∠2,判定△AMC≌△BMD的方法是 ;
即时测评
SAS
AAS
ASA
例2 如图,已知△ABC≌△A1B1C1 ,D与D1分别是BC、B1C1上的一点,且BD=B1D1.那么AD=A1D1吗?为什么?
A
B
D
C
A
1
B
1
D
1
C
1
典例精析
[任务二 探究全等三角形的对应“角平分线、中线、高线”之间的关系]
说明两个角相等、两条线段相等的基本方法:说明这两个角或两条线段所在的两个三角形全等。
答:AD=A1D1
证明: ∵△ABC≌△A1B1C1
∴ ∠B=∠B1,AB=A1B1
∵在△ABD和△A1B1D1中
AB=A1B1
∠B=∠B1
BD=B1D1
∴△ABD≌△A1B1D1 (SAS)
∴ AD=A1D1
全等三角形的对应中线、对应角平分线、对应高是否分别相等呢?
要求:先独立完成,然后小组内交流讨论,最后小组展示、点评.
A
B
D
C
A
1
B
1
D
1
C
1
类比推理
已知:如图,△ABC≌△A1B1C1 ,AD、A1D1 分别是△ABC和△A1B1C1 的中线.那么AD = A1D1吗?请说明理由.
问题1
全等三角形的对应中线相等。
问题2
已知:如图,△ABC≌△A1B1C1 ,AD、A1D1 分别是△ABC和△A1B1C1 的角平分线.那么AD = A1D1吗?请说明理由.
全等三角形的对应角平分线相等。
问题3
已知:如图, △ABC≌△A1B1C1 ,AD、 A1D1 分别是△ABC和△A1B1C1 的高. 那么AD = A1D1吗?请说明理由.
全等三角形的对应高相等。
两个全等三角形的面积是否相等 周长呢 你能说明理由吗?
结论:两个全等三角形的面积 ,周长也 .
追问
相等
相等
1.下列说法中:
⑴全等三角形的周长相等、面积相等;
⑵面积相等的两个三角形是全等三角形;
⑶全等三角形对应边上的高、中线及对应角平分线分别相等,其中正确的个数有( )
A.3个 B.2个 C.1个 D.0个
即时测评
B
1.如图,已知:∠B=∠DEF,BC=EF,现要说明△ABC≌△DEF,
(1)若要以“SAS”为依据,还缺条件 ;
(2)若要以“ASA”为依据,还缺条件 ;
(3)若要以“AAS”为依据,还缺条件 .
B
AB=DE
∠ACB=∠DFE
∠A=∠D
2.已知:如图,在△ABC中,D是边BC上一点,BE⊥AD,CF⊥AD,垂足分别为E、F.若AD是△ABC的中线,BE与CF有什么关系?并说明理由.
解:BE∥CF且BE=CF.理由如下:
∵AD是△ABC的中线,
∴BD=CD,
在△BED和△CFD中
∴△BED≌△CFD,
∴BE=CF.
∵BE⊥AD,CF⊥AD,
∴BE∥CF.
综上,BE∥CF且BE=CF.
3.如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE,试说明:△ABC≌△ADE的理由.
解:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
即∠BAC=∠DAE,
∵∠B+∠1=∠ADE+∠3,
且∠1=∠3,
∴∠B=∠ADE,
在△ABC和△ADE中
∴△ABC≌△ADE(AAS).
4.如图,已知在Rt△ABC,AB=AC,∠BAC=90°,AN是过点A的任一条直线,BD⊥AN于D,CE⊥AN于E.试说明:DE=BD﹣CE.
解:∵∠BAC=90°,
∴∠BAD+∠EAC=90°,
又∵BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
∠BAD+∠ABD=90°,
∴∠ABD=∠EAC,
又∵AB=AC,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE=AD+DE=CE+DE,
∴BD=DE+CE,
即DE=BD﹣CE.
今天这节课,我们有哪些收获?
判定三角形全等的四种方法,
会选取恰当的方法解决三角形全等问题。
2. 全等三角形的对应中线、对应高、对应角平分线分别相等。
3. 类比、转化等数学思想的应用。
课堂小结
基础题:1.课后习题第2题
提高题:2.请学有余力的同学课后习题第3、4题,下节课在全班展示、交流。
课后作业
本节课到此结束,谢谢大家!
