1.4 利用三角形全等测距离 课件(共24张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 1.4 利用三角形全等测距离 课件(共24张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
鲁教版七年级上册数学
第一章 三角形
4 利用三角形全等测距离
学习目标
1.复习并归纳三角形全等的判定及性质;
2.能够根据三角形全等测定两点间的距离,并解决实际题.
(重点,难点)
“五羊石像”位于广州市越秀公园内的越秀山木壳岗,主羊头部高高昂起,口中衔穗,回眸微笑,其余四羊环绕于主羊周围,姿态各异,造型优美,已经成为广州城市的标志.如图1所示的“五羊石像”,整个石像连基座高11米,A,B两点分别为石像底座的两端(其中A,B两点均在地面上).如何测量“五羊石像”底座的两端A,B的距离呢?
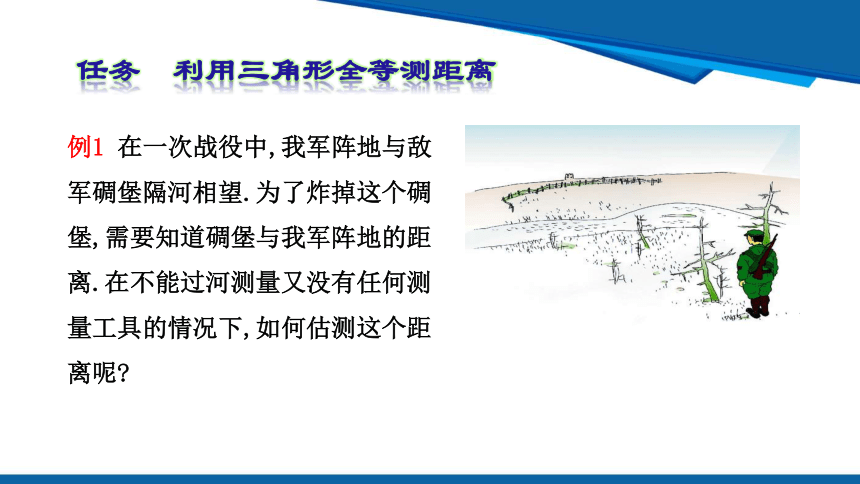
例1 在一次战役中,我军阵地与敌军碉堡隔河相望.为了炸掉这个碉堡,需要知道碉堡与我军阵地的距离.在不能过河测量又没有任何测量工具的情况下,如何估测这个距离呢
任务 利用三角形全等测距离
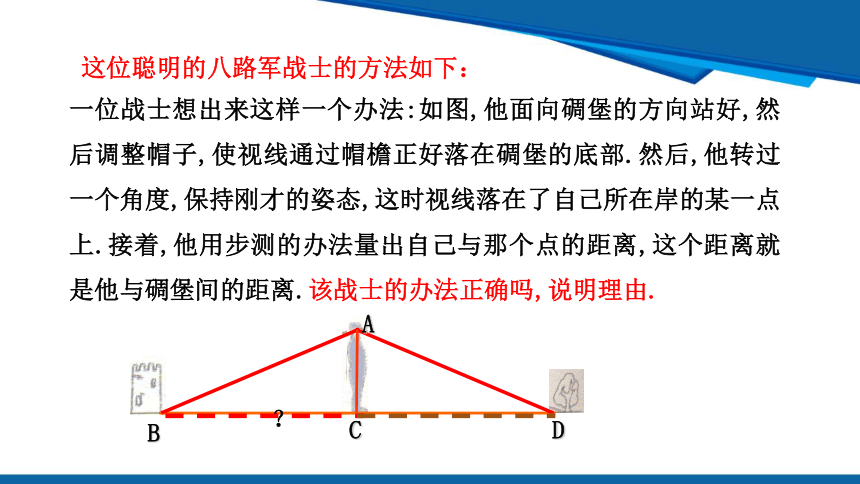
一位战士想出来这样一个办法:如图,他面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部.然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上.接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡间的距离.该战士的办法正确吗,说明理由.
A
C
B
D
?
这位聪明的八路军战士的方法如下:
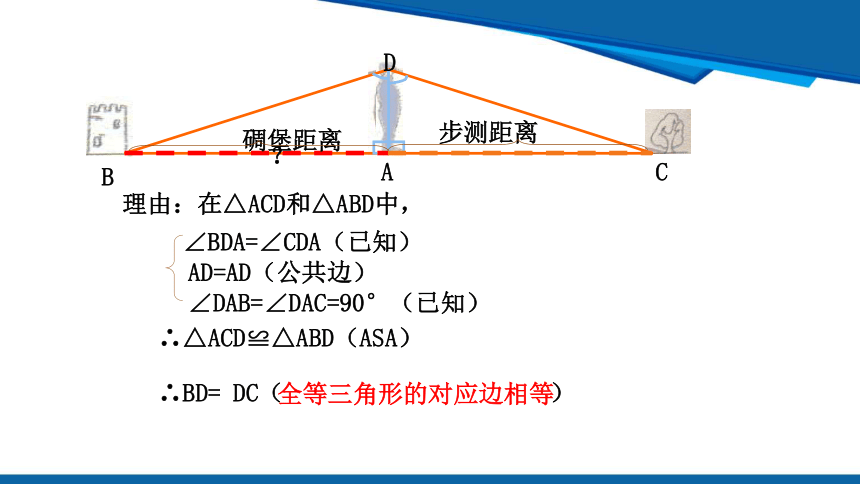
∴BD= DC( )
D
A
B
C
?
理由:在△ACD和△ABD中,
∠BDA=∠CDA(已知)
AD=AD(公共边)
∠DAB=∠DAC=90°(已知)
∴△ACD≌△ABD(ASA)
全等三角形的对应边相等
步测距离
碉堡距离
例2 如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长.他叔叔帮他出了一个这样的主意:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度.
(1)DE的长就是AB的距离吗 请说明理由;
(2)如果DE的长度是8 m,则AB的长度是多少
解:(1)DE与AB相等,理由如下:
在△ABC和△DEC中,
,
∴△ABC≌△DEC(SAS),
∴DE=AB;
(2)由(1)知,DE=AB,
∵DE=8m,
∴AB=8m,
即AB的长度是8m.
利用三角形全等可以测量两点之间的距离.
利用三角形全等测距离,实际上是构造出全等三角形,运用全等三角形的性质(对应边相等),把较难测量的距离转化为较容易测量的线段的长度.
即时测评
1.如图,要测量水池的宽AB,可从点A出发在地面上画一条线段AC,使AC⊥AB,在BA的延长线上找一点D,使∠ACD=∠ACB,这时量得AD=110m,则水池的宽AB是________ m.
110
2.如图所示,已知AC=DB,AO=DO,CD=100 m,则A,B两点间的距离( )
A.大于100 m
B.等于100 m
C.小于100 m
D.无法确定
C
即时测评
3.如图,要测量河中礁石A离岸边B点的距离,采取的方法如下:顺着河岸的方向任作一条线段BC,作∠CBA′=∠CBA,∠BCA′=∠BCA.可得△A′BC≌△ABC,所以A′B=AB,所以测量A′B的长即可得AB的长.判定图中两个三角形全等的理由是( )
A.SAS B.ASA
C.SSS D.AAS
B
即时测评
即时测评
4.小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?
解:∵∠CPD=36°,∠APB=54°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=54°.
在△CPD和△PAB中,
∵∠CDP=∠ABP,DC=PB,∠DCP=∠APB,
∴△CPD≌△PAB(ASA),
∴DP=AB.
∵DB=36米,PB=10米,
∴AB=36-10=26(米).
答:楼高AB是26米.
1.如图,小明用10块高度都是1 cm的相同的长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放一个等腰直角三角尺ABC,点C在DE上,点A,B分别与木墙的顶端重合,则两堵木墙之间的距离为_________ cm.
10
2.如图,要测量河岸相对两点A,B的距离,可以从AB的垂线BF上取两点C,D,使BC=CD.过点D作DE⊥BF,且A,C,E三点在一直线上.若测得DE=15米,即可知道AB也为15米.请说明理由.
解:∵AB⊥BF,DE⊥BF,
∴∠ABC=∠EDC=90°,
在△ABC和△EDC中,
∴△ABC≌△EDC(ASA),
∴AB=DE,
故测得DE=15米,即可知道AB也为15米.
3.某数学兴趣小组设计方案测量河两岸A、B两点间的距离.如图所示,在点B所在河岸同侧的平地上取点C和点D,使得点A,B,C在同一直线上,且CD=BC,在CD的延长线上取点E,使得∠CEB=15°,测得∠ACD=100°,∠ADC=65°,DE的长度为30米.请你根据以上数据求出A、B两点间的距离,并说明理由.
解:∵∠C=100°,∠ADC=65°,
∴∠CAD=15°,
∴∠CAD=∠BEC,
在△ACD与△ECB中,
∴△ACD≌△ECB(AAS),
∴AC=CE,
又∵CB=CD,
∴AB=DE=30米,
答:A、B两点间的距离为30米.
课堂小结
知识:利用三角形全等测距离的目的:变不可测距离为可测距离.
依据:全等三角形的性质.
关键:构造全等三角形.
方法:(1)延长法构造全等三角形;
(2)垂直法构造全等三角形.
基础题:1.课后习题第 1题
提高题:2.请学有余力的同学做课后习题第3、4题,下节课在全班展示、交流。
课后作业
本节课到此结束,谢谢大家!
鲁教版七年级上册数学
第一章 三角形
4 利用三角形全等测距离
学习目标
1.复习并归纳三角形全等的判定及性质;
2.能够根据三角形全等测定两点间的距离,并解决实际题.
(重点,难点)
“五羊石像”位于广州市越秀公园内的越秀山木壳岗,主羊头部高高昂起,口中衔穗,回眸微笑,其余四羊环绕于主羊周围,姿态各异,造型优美,已经成为广州城市的标志.如图1所示的“五羊石像”,整个石像连基座高11米,A,B两点分别为石像底座的两端(其中A,B两点均在地面上).如何测量“五羊石像”底座的两端A,B的距离呢?
例1 在一次战役中,我军阵地与敌军碉堡隔河相望.为了炸掉这个碉堡,需要知道碉堡与我军阵地的距离.在不能过河测量又没有任何测量工具的情况下,如何估测这个距离呢
任务 利用三角形全等测距离
一位战士想出来这样一个办法:如图,他面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部.然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上.接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡间的距离.该战士的办法正确吗,说明理由.
A
C
B
D
?
这位聪明的八路军战士的方法如下:
∴BD= DC( )
D
A
B
C
?
理由:在△ACD和△ABD中,
∠BDA=∠CDA(已知)
AD=AD(公共边)
∠DAB=∠DAC=90°(已知)
∴△ACD≌△ABD(ASA)
全等三角形的对应边相等
步测距离
碉堡距离
例2 如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长.他叔叔帮他出了一个这样的主意:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度.
(1)DE的长就是AB的距离吗 请说明理由;
(2)如果DE的长度是8 m,则AB的长度是多少
解:(1)DE与AB相等,理由如下:
在△ABC和△DEC中,
,
∴△ABC≌△DEC(SAS),
∴DE=AB;
(2)由(1)知,DE=AB,
∵DE=8m,
∴AB=8m,
即AB的长度是8m.
利用三角形全等可以测量两点之间的距离.
利用三角形全等测距离,实际上是构造出全等三角形,运用全等三角形的性质(对应边相等),把较难测量的距离转化为较容易测量的线段的长度.
即时测评
1.如图,要测量水池的宽AB,可从点A出发在地面上画一条线段AC,使AC⊥AB,在BA的延长线上找一点D,使∠ACD=∠ACB,这时量得AD=110m,则水池的宽AB是________ m.
110
2.如图所示,已知AC=DB,AO=DO,CD=100 m,则A,B两点间的距离( )
A.大于100 m
B.等于100 m
C.小于100 m
D.无法确定
C
即时测评
3.如图,要测量河中礁石A离岸边B点的距离,采取的方法如下:顺着河岸的方向任作一条线段BC,作∠CBA′=∠CBA,∠BCA′=∠BCA.可得△A′BC≌△ABC,所以A′B=AB,所以测量A′B的长即可得AB的长.判定图中两个三角形全等的理由是( )
A.SAS B.ASA
C.SSS D.AAS
B
即时测评
即时测评
4.小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?
解:∵∠CPD=36°,∠APB=54°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=54°.
在△CPD和△PAB中,
∵∠CDP=∠ABP,DC=PB,∠DCP=∠APB,
∴△CPD≌△PAB(ASA),
∴DP=AB.
∵DB=36米,PB=10米,
∴AB=36-10=26(米).
答:楼高AB是26米.
1.如图,小明用10块高度都是1 cm的相同的长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放一个等腰直角三角尺ABC,点C在DE上,点A,B分别与木墙的顶端重合,则两堵木墙之间的距离为_________ cm.
10
2.如图,要测量河岸相对两点A,B的距离,可以从AB的垂线BF上取两点C,D,使BC=CD.过点D作DE⊥BF,且A,C,E三点在一直线上.若测得DE=15米,即可知道AB也为15米.请说明理由.
解:∵AB⊥BF,DE⊥BF,
∴∠ABC=∠EDC=90°,
在△ABC和△EDC中,
∴△ABC≌△EDC(ASA),
∴AB=DE,
故测得DE=15米,即可知道AB也为15米.
3.某数学兴趣小组设计方案测量河两岸A、B两点间的距离.如图所示,在点B所在河岸同侧的平地上取点C和点D,使得点A,B,C在同一直线上,且CD=BC,在CD的延长线上取点E,使得∠CEB=15°,测得∠ACD=100°,∠ADC=65°,DE的长度为30米.请你根据以上数据求出A、B两点间的距离,并说明理由.
解:∵∠C=100°,∠ADC=65°,
∴∠CAD=15°,
∴∠CAD=∠BEC,
在△ACD与△ECB中,
∴△ACD≌△ECB(AAS),
∴AC=CE,
又∵CB=CD,
∴AB=DE=30米,
答:A、B两点间的距离为30米.
课堂小结
知识:利用三角形全等测距离的目的:变不可测距离为可测距离.
依据:全等三角形的性质.
关键:构造全等三角形.
方法:(1)延长法构造全等三角形;
(2)垂直法构造全等三角形.
基础题:1.课后习题第 1题
提高题:2.请学有余力的同学做课后习题第3、4题,下节课在全班展示、交流。
课后作业
本节课到此结束,谢谢大家!
