2.2 简单的轴对称图形 第3课时 等腰三角形的性质 课件(共37张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 2.2 简单的轴对称图形 第3课时 等腰三角形的性质 课件(共37张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 08:11:34 | ||
图片预览







文档简介
(共37张PPT)
第二章 轴对称
2 简单的轴对称图形
第3课时 等腰三角形的性质
学习目标
1.探索并了解等腰三角形的性质;
2.知道等边三角形是特殊的等腰三角形,并掌握其性质.
3.在探索轴对称性质的过程中,能够进行有条理地思考并进行简单地推理.
观察下列各种图形,判断是不是轴对称图形,能找出对称轴吗?
知识回顾
观察下列各种图形,判断是不是轴对称图形,能找出对称轴吗?
知识回顾
在生活中,我们经常能看到这样的建筑.
仔细观察这几张图片,它们的形状与什么图形类似呢
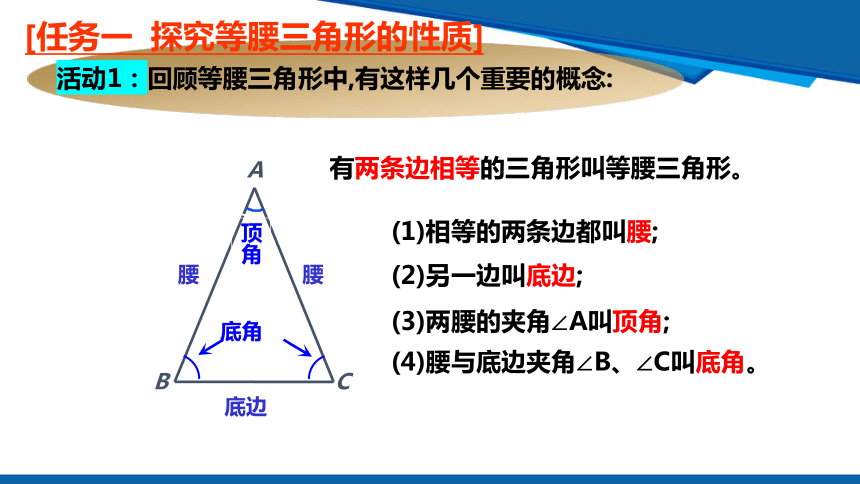
活动1:回顾等腰三角形中,有这样几个重要的概念:
A
B
C
底边
腰
腰
顶角
底角
(1)相等的两条边都叫腰;
(2)另一边叫底边;
(3)两腰的夹角∠A叫顶角;
(4)腰与底边夹角∠B、∠C叫底角。
有两条边相等的三角形叫等腰三角形。
[任务一 探究等腰三角形的性质]
4
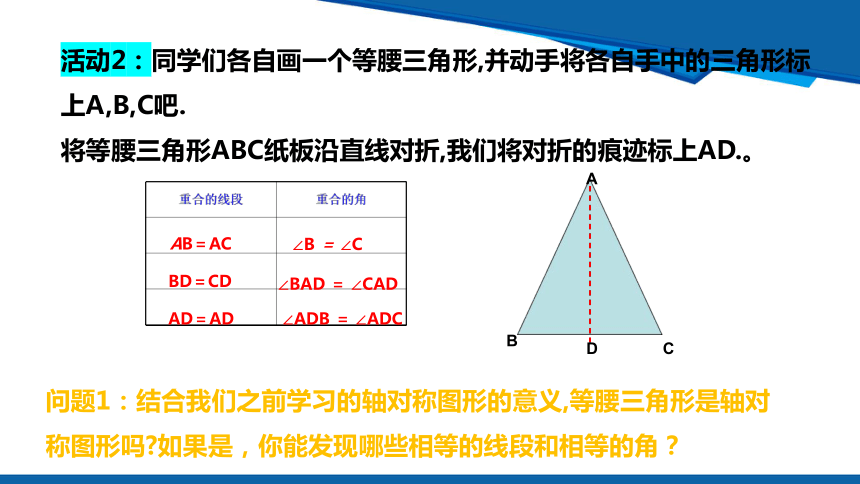
AB=AC
∠B = ∠C
BD=CD
∠BAD = ∠CAD
AD=AD
∠ADB = ∠ADC
A
B
D
C
活动2:同学们各自画一个等腰三角形,并动手将各自手中的三角形标上A,B,C吧.
将等腰三角形ABC纸板沿直线对折,我们将对折的痕迹标上AD.。
问题1:结合我们之前学习的轴对称图形的意义,等腰三角形是轴对称图形吗 如果是,你能发现哪些相等的线段和相等的角?
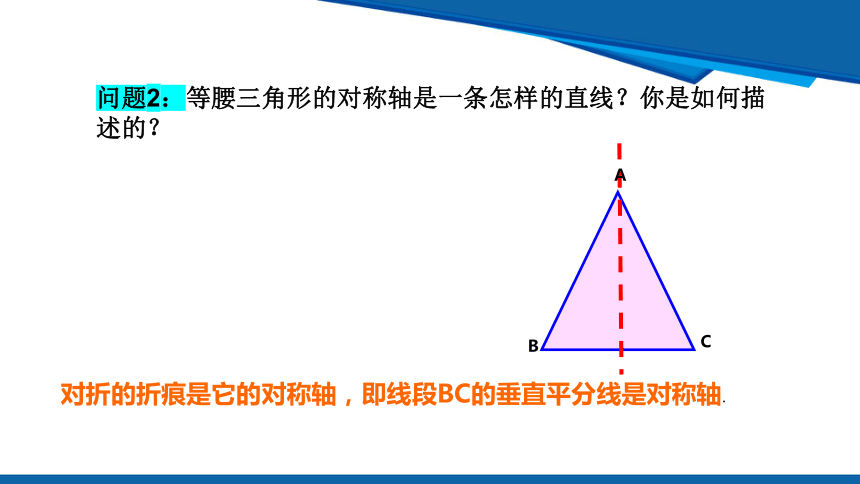
问题2:等腰三角形的对称轴是一条怎样的直线?你是如何描述的?
对折的折痕是它的对称轴,即线段BC的垂直平分线是对称轴.
A
B
C
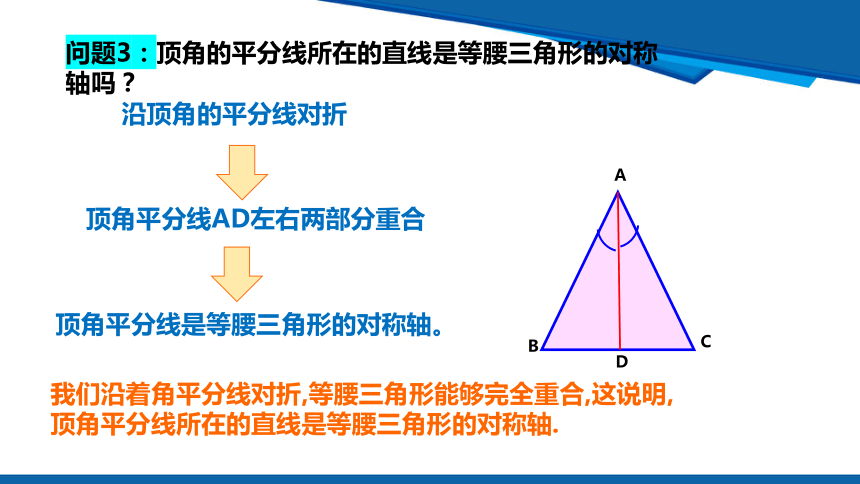
问题3:顶角的平分线所在的直线是等腰三角形的对称轴吗?
A
B
C
D
沿顶角的平分线对折
顶角平分线AD左右两部分重合
顶角平分线是等腰三角形的对称轴。
我们沿着角平分线对折,等腰三角形能够完全重合,这说明,顶角平分线所在的直线是等腰三角形的对称轴.
问题4:底边上的中线所在的直线是等腰三角形的对称轴吗 底边上的高所在的直线呢
A
B
C
底边上的中线所在的直线是等腰三角形的对称轴.底边上的高所在的直线是等腰三角形的对称轴
你能总结这个现象吗?
等腰三角形是轴对称图形.
等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称 “三线合一” ),它们所在的直线都是等腰三角形的对称轴.
等腰三角形的两个底角相等.
AD是底边上的高
AD垂直于BC
AD是底边上的中线
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合。(等腰三角形三线合一)
AD平分∠BAC
AD是BC的中线
AD是顶角平分线
A
B
D
C
∠1= ∠ 2
∠ADB= ∠ ADC=900
BD=CD
2
1
等腰三角形的性质2
等腰三角形是轴对称图形.
等腰三角形的性质1
等腰三角形的两个底角相等
(简写成“等边对等角”)
用符号语言表示为:
在△ABC中,
∵ AB=AC
∴ ∠B=∠C ( )
等边对等角
等腰三角形的性质3
A
B
C
典例精析
例1.已知一个等腰三角形的底角是顶角的2倍,求它的各个内角的度。
解:设顶角为x度,则底角为2x度,则:x+2x+2x=180,
解得:x=36,
所以这个三角形三个内角的度数分别为36°,72°,72°。
即时测评
1.如图,在△ABC中,AB=AC,∠B=40°,AC的垂直平分线DE分别交AC,BC于点D,E,则∠BAE的度数为( )
A.50° B.40° C.60° D.80°
2.如图,在△ABC中,AB=AC,∠B=70°,
AD是BC边上的中线,E是AC边上一点.
若DE=DC,则∠ADE的度数为 .
C
50°
3.如图,△ABC中,∠A=36°,D在边AC上,AD=BD=BC,求∠DBC的度数.
解:∵BD=AD,
∴∠A=∠ABD=36°,
∴∠BDC=∠A+∠ABD=72°,
∵BD=BC,
∴∠BDC=∠BCD=72°,
∴∠DBC=180°﹣72°﹣72°=36°.
三边都相等的三角形是等边三角形,也叫正三角形。
问题1:由于等边三角形是特殊的等腰三角形,那么等边三角形肯定也是轴对称图形,那它的对称轴有几条呢 为什么?
由于等边三角形的三边都是相等的,因此,无论从哪个角进行对折,都是重合的,因此,等边三角形有三条对称轴.
[任务二 探究等边三角形的性质]
问题2:等腰三角形所具有的三线合一的性质,等边三角形也具有这个性质吗?
等边三角形页具有“三线合一”的性质.
问题3:等腰三角形具有“等边对等角”性质,等边三角形中具有这样的性质吗?它的三个角有什么特征?
它的三个角都是相等的,都为60°
等边三角形的性质:
1.等边三角形是轴对称图形。等边三角形共有三条对称轴。
2.等边三角形每个角的平分线和这个角的对边上的中线、高线重合(“三线合一”),它们所在的直线都是等边三角形的对称轴。
3.等边三角形的各角都相等,都等于60°。
总结
例2 已知,如图,P、Q是△ABC边BC上两点,且BP=PQ= QC=AP=AQ,求∠BAC的度数。
解:∵ BP=PQ=QC=AP=AQ
∴ ∠PAQ= ∠APQ =∠AQP,
∠B=∠BAP,∠C=∠CAQ 。
又∵ ∠BAP+ ∠ABP= ∠APQ, ∠C+∠CAQ =∠AQP
∴ ∠BAP= ∠CAQ =30°,
∴ ∠BAC=120°。
△APQ是等边三角形
典例精析
即时测评
1.如图,在等边△ABC中,AD⊥BC,BE⊥AC,AD,BE交于点F,则∠AFE的度数是( )
A.60° B.50° C.40° D.30°
2.如图,在等边三角形ABC中,AD平分∠BAC,
若BC=10,则CD的长为 .
A
5
3.如图,△ABC为等边三角形,点M是线段BC上的任意一点,点N是线段CA上任意一点,且BM=CN,直线BN与AM交于点Q.
(1)求证:△BAN≌△ACM;
解:(1)∵△ABC为等边三角形,
∴AB=BC=CA,∠BAC=∠BCA=60°,
∵BM=CN,
∴CM=AN,
又∵∠BAN=∠ACM,
∴△BAN≌△ACM;
(2)求∠BQM的大小.
(2)∴∠CAM=∠ABN,
∴∠BQM=∠ABN+∠BAQ
=∠CAM+∠BAQ
=∠BAC
=60°.
1.如果等腰三角形两边长是9cm和4cm,那么它的周长
是( )
A.17cm B.22cm C.17或22cm D.无法确定
B
分腰为9cm和4cm两种情况讨论
2.下列说法错误的是( )
A.等腰三角形的高、中线、角平分线互相重合
B.三角形两边的垂直平分线的交点到三个顶点距离相等
C.等腰三角形的两个底角相等
D.等腰三角形顶角的外角是底角的二倍
A
3.已知:如图,AD是等腰三角形ABC的底边BC上的中线,P是AD上任意一点.求证:∠ABP=∠ACP。
证明:∵△ABC中,AB=AC,AD为BC边的中线,
∴△ABP≌△ACP(SAS),
∴∠ABP=∠ACP。
∴AD是角平分线,
∴∠BAP=∠CAP,
在△ABP与△ACP中,
AB=AC
∠BAP=∠CAP
AP=AP
4.如图所示的三角测平架中,AB=AC,在BC的中点D挂一个重锤,自然下垂,整架身,使点A恰好在重锤线上,试问:此时BC是否正好处于水平位置?为什么?
解:这时BC处于水平位置.
∵D是BC的中点,
∴BD=DC,
∵AB=AC,
∴AD⊥BC(三线合一).
∵重锤线与地平线垂直,
∴BC处于水平位置。
5. 如图,△ABC、△ADE是等边三角形,B、C、D在同一直线上.试说明:
(1)CE=AC+DC;
(2)∠ECD=60°.
解:(1)∵△ABC、△ADE是等边三角形,
∴AE=AD,BC=AC=AB,
∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴BD=EC,
∵BD=BC+CD=AC+CD,
∴CE=BD=AC+CD;
(2)由(1)知:△BAD≌△CAE,
∴∠ACE=∠ABD=60°,
∴∠ECD=180°﹣∠ACB﹣∠ACE=60°,
∴∠ECD=60°.
等腰三角形
等边对等角
三线合一
等边三角形
每个内角都为60°
三条对称轴
三线合一
课堂小结
基础题:1.课后习题第 2题
提高题:2.请学有余力的同学做课后习题第3、4题,下节课在班内展示、交流。
课后作业
本节课到此结束,
谢谢大家!
第二章 轴对称
2 简单的轴对称图形
第3课时 等腰三角形的性质
学习目标
1.探索并了解等腰三角形的性质;
2.知道等边三角形是特殊的等腰三角形,并掌握其性质.
3.在探索轴对称性质的过程中,能够进行有条理地思考并进行简单地推理.
观察下列各种图形,判断是不是轴对称图形,能找出对称轴吗?
知识回顾
观察下列各种图形,判断是不是轴对称图形,能找出对称轴吗?
知识回顾
在生活中,我们经常能看到这样的建筑.
仔细观察这几张图片,它们的形状与什么图形类似呢
活动1:回顾等腰三角形中,有这样几个重要的概念:
A
B
C
底边
腰
腰
顶角
底角
(1)相等的两条边都叫腰;
(2)另一边叫底边;
(3)两腰的夹角∠A叫顶角;
(4)腰与底边夹角∠B、∠C叫底角。
有两条边相等的三角形叫等腰三角形。
[任务一 探究等腰三角形的性质]
4
AB=AC
∠B = ∠C
BD=CD
∠BAD = ∠CAD
AD=AD
∠ADB = ∠ADC
A
B
D
C
活动2:同学们各自画一个等腰三角形,并动手将各自手中的三角形标上A,B,C吧.
将等腰三角形ABC纸板沿直线对折,我们将对折的痕迹标上AD.。
问题1:结合我们之前学习的轴对称图形的意义,等腰三角形是轴对称图形吗 如果是,你能发现哪些相等的线段和相等的角?
问题2:等腰三角形的对称轴是一条怎样的直线?你是如何描述的?
对折的折痕是它的对称轴,即线段BC的垂直平分线是对称轴.
A
B
C
问题3:顶角的平分线所在的直线是等腰三角形的对称轴吗?
A
B
C
D
沿顶角的平分线对折
顶角平分线AD左右两部分重合
顶角平分线是等腰三角形的对称轴。
我们沿着角平分线对折,等腰三角形能够完全重合,这说明,顶角平分线所在的直线是等腰三角形的对称轴.
问题4:底边上的中线所在的直线是等腰三角形的对称轴吗 底边上的高所在的直线呢
A
B
C
底边上的中线所在的直线是等腰三角形的对称轴.底边上的高所在的直线是等腰三角形的对称轴
你能总结这个现象吗?
等腰三角形是轴对称图形.
等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称 “三线合一” ),它们所在的直线都是等腰三角形的对称轴.
等腰三角形的两个底角相等.
AD是底边上的高
AD垂直于BC
AD是底边上的中线
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合。(等腰三角形三线合一)
AD平分∠BAC
AD是BC的中线
AD是顶角平分线
A
B
D
C
∠1= ∠ 2
∠ADB= ∠ ADC=900
BD=CD
2
1
等腰三角形的性质2
等腰三角形是轴对称图形.
等腰三角形的性质1
等腰三角形的两个底角相等
(简写成“等边对等角”)
用符号语言表示为:
在△ABC中,
∵ AB=AC
∴ ∠B=∠C ( )
等边对等角
等腰三角形的性质3
A
B
C
典例精析
例1.已知一个等腰三角形的底角是顶角的2倍,求它的各个内角的度。
解:设顶角为x度,则底角为2x度,则:x+2x+2x=180,
解得:x=36,
所以这个三角形三个内角的度数分别为36°,72°,72°。
即时测评
1.如图,在△ABC中,AB=AC,∠B=40°,AC的垂直平分线DE分别交AC,BC于点D,E,则∠BAE的度数为( )
A.50° B.40° C.60° D.80°
2.如图,在△ABC中,AB=AC,∠B=70°,
AD是BC边上的中线,E是AC边上一点.
若DE=DC,则∠ADE的度数为 .
C
50°
3.如图,△ABC中,∠A=36°,D在边AC上,AD=BD=BC,求∠DBC的度数.
解:∵BD=AD,
∴∠A=∠ABD=36°,
∴∠BDC=∠A+∠ABD=72°,
∵BD=BC,
∴∠BDC=∠BCD=72°,
∴∠DBC=180°﹣72°﹣72°=36°.
三边都相等的三角形是等边三角形,也叫正三角形。
问题1:由于等边三角形是特殊的等腰三角形,那么等边三角形肯定也是轴对称图形,那它的对称轴有几条呢 为什么?
由于等边三角形的三边都是相等的,因此,无论从哪个角进行对折,都是重合的,因此,等边三角形有三条对称轴.
[任务二 探究等边三角形的性质]
问题2:等腰三角形所具有的三线合一的性质,等边三角形也具有这个性质吗?
等边三角形页具有“三线合一”的性质.
问题3:等腰三角形具有“等边对等角”性质,等边三角形中具有这样的性质吗?它的三个角有什么特征?
它的三个角都是相等的,都为60°
等边三角形的性质:
1.等边三角形是轴对称图形。等边三角形共有三条对称轴。
2.等边三角形每个角的平分线和这个角的对边上的中线、高线重合(“三线合一”),它们所在的直线都是等边三角形的对称轴。
3.等边三角形的各角都相等,都等于60°。
总结
例2 已知,如图,P、Q是△ABC边BC上两点,且BP=PQ= QC=AP=AQ,求∠BAC的度数。
解:∵ BP=PQ=QC=AP=AQ
∴ ∠PAQ= ∠APQ =∠AQP,
∠B=∠BAP,∠C=∠CAQ 。
又∵ ∠BAP+ ∠ABP= ∠APQ, ∠C+∠CAQ =∠AQP
∴ ∠BAP= ∠CAQ =30°,
∴ ∠BAC=120°。
△APQ是等边三角形
典例精析
即时测评
1.如图,在等边△ABC中,AD⊥BC,BE⊥AC,AD,BE交于点F,则∠AFE的度数是( )
A.60° B.50° C.40° D.30°
2.如图,在等边三角形ABC中,AD平分∠BAC,
若BC=10,则CD的长为 .
A
5
3.如图,△ABC为等边三角形,点M是线段BC上的任意一点,点N是线段CA上任意一点,且BM=CN,直线BN与AM交于点Q.
(1)求证:△BAN≌△ACM;
解:(1)∵△ABC为等边三角形,
∴AB=BC=CA,∠BAC=∠BCA=60°,
∵BM=CN,
∴CM=AN,
又∵∠BAN=∠ACM,
∴△BAN≌△ACM;
(2)求∠BQM的大小.
(2)∴∠CAM=∠ABN,
∴∠BQM=∠ABN+∠BAQ
=∠CAM+∠BAQ
=∠BAC
=60°.
1.如果等腰三角形两边长是9cm和4cm,那么它的周长
是( )
A.17cm B.22cm C.17或22cm D.无法确定
B
分腰为9cm和4cm两种情况讨论
2.下列说法错误的是( )
A.等腰三角形的高、中线、角平分线互相重合
B.三角形两边的垂直平分线的交点到三个顶点距离相等
C.等腰三角形的两个底角相等
D.等腰三角形顶角的外角是底角的二倍
A
3.已知:如图,AD是等腰三角形ABC的底边BC上的中线,P是AD上任意一点.求证:∠ABP=∠ACP。
证明:∵△ABC中,AB=AC,AD为BC边的中线,
∴△ABP≌△ACP(SAS),
∴∠ABP=∠ACP。
∴AD是角平分线,
∴∠BAP=∠CAP,
在△ABP与△ACP中,
AB=AC
∠BAP=∠CAP
AP=AP
4.如图所示的三角测平架中,AB=AC,在BC的中点D挂一个重锤,自然下垂,整架身,使点A恰好在重锤线上,试问:此时BC是否正好处于水平位置?为什么?
解:这时BC处于水平位置.
∵D是BC的中点,
∴BD=DC,
∵AB=AC,
∴AD⊥BC(三线合一).
∵重锤线与地平线垂直,
∴BC处于水平位置。
5. 如图,△ABC、△ADE是等边三角形,B、C、D在同一直线上.试说明:
(1)CE=AC+DC;
(2)∠ECD=60°.
解:(1)∵△ABC、△ADE是等边三角形,
∴AE=AD,BC=AC=AB,
∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴BD=EC,
∵BD=BC+CD=AC+CD,
∴CE=BD=AC+CD;
(2)由(1)知:△BAD≌△CAE,
∴∠ACE=∠ABD=60°,
∴∠ECD=180°﹣∠ACB﹣∠ACE=60°,
∴∠ECD=60°.
等腰三角形
等边对等角
三线合一
等边三角形
每个内角都为60°
三条对称轴
三线合一
课堂小结
基础题:1.课后习题第 2题
提高题:2.请学有余力的同学做课后习题第3、4题,下节课在班内展示、交流。
课后作业
本节课到此结束,
谢谢大家!
