2.3 利用轴对称进行设计 课件(共24张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 2.3 利用轴对称进行设计 课件(共24张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 08:12:48 | ||
图片预览






文档简介
(共24张PPT)
第二章 轴对称
3 利用轴对称进行设计
学习目标
1.进一步理解轴对称及其性质.
2.能按要求把所给出的图形补成以某直线为轴的轴对称图形。
3.能依据图形的轴对称关系设计轴对称图形。
[任务一 探究剪纸中的轴对称图形]
1.取一张长30 cm、宽6 cm的纸条,将它每3 cm一段,一反一正像“手风琴”那样折叠起来.在折叠好的纸上画出字母E,并用小刀把画出的字母E挖去. 拉开“手风琴”纸条,你就可以得到一条以字母E为图案的花边.
在上面的活动中,如果先把纸条纵向对折,再折成“手风琴”,然后继续上面的步骤,此时会得到怎样的花边?它是轴对称图形吗?先猜一猜,再做 一做.
思考?
典例精析
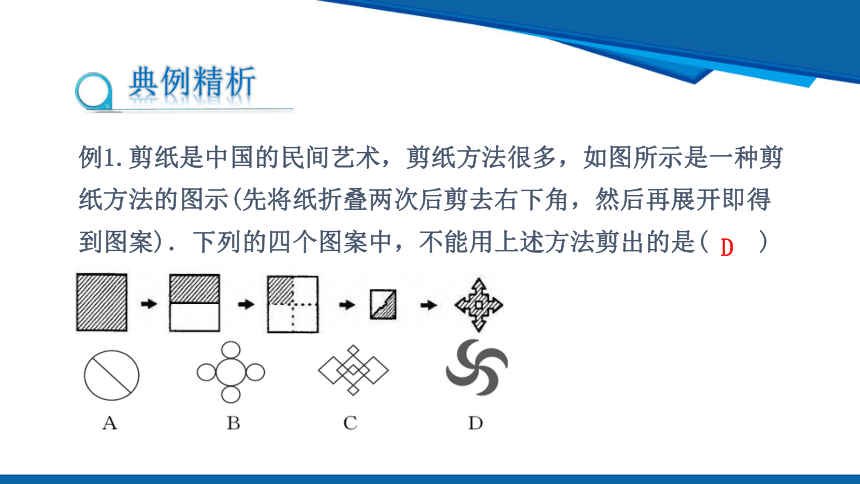
例1.剪纸是中国的民间艺术,剪纸方法很多,如图所示是一种剪纸方法的图示(先将纸折叠两次后剪去右下角,然后再展开即得到图案).下列的四个图案中,不能用上述方法剪出的是( )
D
即时测评
1.将一圆形纸片对折后再对折得到如图所示的扇形,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是( ).
A.
B.
C.
D.
A
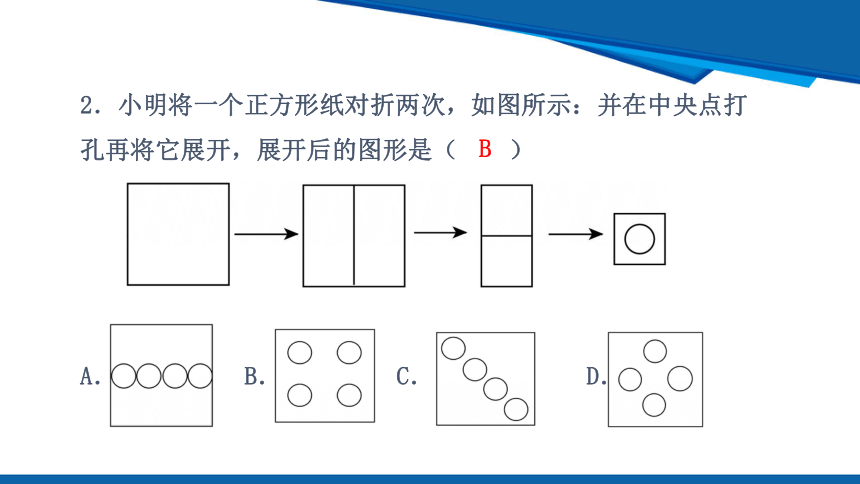
2.小明将一个正方形纸对折两次,如图所示:并在中央点打孔再将它展开,展开后的图形是( )
A. B. C. D.
B
活动2
如图所示,取一张薄的正方形纸,沿对角线对折后,得到一个等腰直角三角形,再沿底边上的高线对折.将得到的角形纸沿图中的黑色线剪开,去掉含 90°角的部分.打开折叠的纸, 并将其铺平.
[任务二 探究折叠中的轴对称图形]
问题1:你会得到怎样的图案?先猜一猜,再做一做.
问题2:你能说明为什么会得到这样的图案吗?应用学过的轴对称知识试一试.
得到的是一个轴对称图案.
按上面的做法,实际上折出了正方形的两条对称轴,因此我们得到的图案一定有2条对称轴.
问题3:如果将正方形纸按上面方式对折 3 次,然后沿圆弧剪开,去掉较小部分,展开后结果又会怎样?为什么?
问题4: 当纸对折 2 次后,剪出的图案至少有几条对称轴?3次呢?
当纸对折 2 次后,剪出的图案至少有2条对称轴;当纸对折 3 次后,剪出的图案至少有4条对称轴.
将正方形对折3次后,按图剪切后,展开的图案仍是一个轴对称图形,并且它有四条对称轴.
总结:剪纸的原理是轴对称和轴对称图形的性质的应用,纸上的折痕所在的直线就是相邻两个图案的对称轴.
剪纸的步骤是:折—画—剪—展.
活动3
生活中有很多具有轴对称性质的图案,例如:
你知道这些图案的含义吗?自己设计一个轴对称图案,并说明你的设计意图.
[任务三 设计轴对称图形]
典例精讲
例3利用一条线段、一个圆、一个正三角形设计一个轴对称图案,并说明你所要表达的含义.
解:如图所示.此图形可以代表一个电灯泡.
即时测评
1.某居民小区搞绿化,要在一块长方形空地(如下图)上建花坛,现征集设计方案,要求设计的图案由圆和正方形组成(圆与正方形的个数不限),并且使整个矩形场地成轴对称图形.请在下边长方形中画出你的设计方案.
解:如图所示.
1.把一张圆形纸片按照先左右对折、再上下对折,然后剪出图案,最后完全展开的步骤会得到( )
A.
B.
C.
D.
D
2.把一张正方形纸片按如图①、图②对折两次后,得到图③,并在其中挖去一个三角形小孔,请你画出展开后的图形(折痕用虚线画出).
解:当正方形纸片两次沿对角线对折成为一直角三角形时,在直角三角形中间的位置上剪三角形形,则直角顶点处完好,即原正方形中间无损,且三角形关于对角线对称,三角形的AB边平行于正方形的边.
.
3.将一个正方形按下列要求割成4块:
(1)分割后的整个图形必须是轴对称图形;
(2)所分得的4块图形是全等图形.
请你按照上述两个要求,分别在图①,②,③中的正方形中画出3种不同的分割方法.(不写画法)
解:能;答案不唯一,如图.
课堂小结:
1.剪纸中的轴对称
2.折叠中的轴对称
3.设计轴对称图形
基础题:1.课后习题第 2题
提高题:2.请学有余力的同学采取合理的方式,搜集整理与本节课有关的“好题”,被选中的同学下节课为全班展示。
课后作业
本节课到此结束,
谢谢大家!
第二章 轴对称
3 利用轴对称进行设计
学习目标
1.进一步理解轴对称及其性质.
2.能按要求把所给出的图形补成以某直线为轴的轴对称图形。
3.能依据图形的轴对称关系设计轴对称图形。
[任务一 探究剪纸中的轴对称图形]
1.取一张长30 cm、宽6 cm的纸条,将它每3 cm一段,一反一正像“手风琴”那样折叠起来.在折叠好的纸上画出字母E,并用小刀把画出的字母E挖去. 拉开“手风琴”纸条,你就可以得到一条以字母E为图案的花边.
在上面的活动中,如果先把纸条纵向对折,再折成“手风琴”,然后继续上面的步骤,此时会得到怎样的花边?它是轴对称图形吗?先猜一猜,再做 一做.
思考?
典例精析
例1.剪纸是中国的民间艺术,剪纸方法很多,如图所示是一种剪纸方法的图示(先将纸折叠两次后剪去右下角,然后再展开即得到图案).下列的四个图案中,不能用上述方法剪出的是( )
D
即时测评
1.将一圆形纸片对折后再对折得到如图所示的扇形,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是( ).
A.
B.
C.
D.
A
2.小明将一个正方形纸对折两次,如图所示:并在中央点打孔再将它展开,展开后的图形是( )
A. B. C. D.
B
活动2
如图所示,取一张薄的正方形纸,沿对角线对折后,得到一个等腰直角三角形,再沿底边上的高线对折.将得到的角形纸沿图中的黑色线剪开,去掉含 90°角的部分.打开折叠的纸, 并将其铺平.
[任务二 探究折叠中的轴对称图形]
问题1:你会得到怎样的图案?先猜一猜,再做一做.
问题2:你能说明为什么会得到这样的图案吗?应用学过的轴对称知识试一试.
得到的是一个轴对称图案.
按上面的做法,实际上折出了正方形的两条对称轴,因此我们得到的图案一定有2条对称轴.
问题3:如果将正方形纸按上面方式对折 3 次,然后沿圆弧剪开,去掉较小部分,展开后结果又会怎样?为什么?
问题4: 当纸对折 2 次后,剪出的图案至少有几条对称轴?3次呢?
当纸对折 2 次后,剪出的图案至少有2条对称轴;当纸对折 3 次后,剪出的图案至少有4条对称轴.
将正方形对折3次后,按图剪切后,展开的图案仍是一个轴对称图形,并且它有四条对称轴.
总结:剪纸的原理是轴对称和轴对称图形的性质的应用,纸上的折痕所在的直线就是相邻两个图案的对称轴.
剪纸的步骤是:折—画—剪—展.
活动3
生活中有很多具有轴对称性质的图案,例如:
你知道这些图案的含义吗?自己设计一个轴对称图案,并说明你的设计意图.
[任务三 设计轴对称图形]
典例精讲
例3利用一条线段、一个圆、一个正三角形设计一个轴对称图案,并说明你所要表达的含义.
解:如图所示.此图形可以代表一个电灯泡.
即时测评
1.某居民小区搞绿化,要在一块长方形空地(如下图)上建花坛,现征集设计方案,要求设计的图案由圆和正方形组成(圆与正方形的个数不限),并且使整个矩形场地成轴对称图形.请在下边长方形中画出你的设计方案.
解:如图所示.
1.把一张圆形纸片按照先左右对折、再上下对折,然后剪出图案,最后完全展开的步骤会得到( )
A.
B.
C.
D.
D
2.把一张正方形纸片按如图①、图②对折两次后,得到图③,并在其中挖去一个三角形小孔,请你画出展开后的图形(折痕用虚线画出).
解:当正方形纸片两次沿对角线对折成为一直角三角形时,在直角三角形中间的位置上剪三角形形,则直角顶点处完好,即原正方形中间无损,且三角形关于对角线对称,三角形的AB边平行于正方形的边.
.
3.将一个正方形按下列要求割成4块:
(1)分割后的整个图形必须是轴对称图形;
(2)所分得的4块图形是全等图形.
请你按照上述两个要求,分别在图①,②,③中的正方形中画出3种不同的分割方法.(不写画法)
解:能;答案不唯一,如图.
课堂小结:
1.剪纸中的轴对称
2.折叠中的轴对称
3.设计轴对称图形
基础题:1.课后习题第 2题
提高题:2.请学有余力的同学采取合理的方式,搜集整理与本节课有关的“好题”,被选中的同学下节课为全班展示。
课后作业
本节课到此结束,
谢谢大家!
