3.1 探索勾股定理 第1课时 探索勾股定理 课件 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 3.1 探索勾股定理 第1课时 探索勾股定理 课件 2025-2026学年数学鲁教版(五四制)七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
第三章 勾股定理
1 探索勾股定理
第1课时 探索勾股定理
学习目标
1.体验勾股定理的探索过程,由特例猜想勾股定理,再由特例验证勾股定理.
2.会利用勾股定理解释生活中的简单现象.
如图,从电线杆离地面8m处向地面拉一条钢索,如果这条钢索在地面的固定点距离电线杆底部6m,那么需要多长钢索?
课堂导入
创设情境引入新课
如图,从电线杆离地面8 m处向地面拉一条钢索,若这条钢索在地面的固定点距离电线杆底部6 m,那么需要多长的钢索
在直角三角形中,任意两条边确定了,另外一条边也就随之确定吗 三边之间存在着一个特定的数量关系.事实上,古人发现,直角三角形的三条边长度的平方存在着一个特殊的关系.
让我们一起去探索吧!
以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
活动1:在纸上作出若干个直角三角形,分别测量它们的三条边,看看三边长的平方之间有什么样的关系 与同伴交流.
[任务 探究勾股定理]
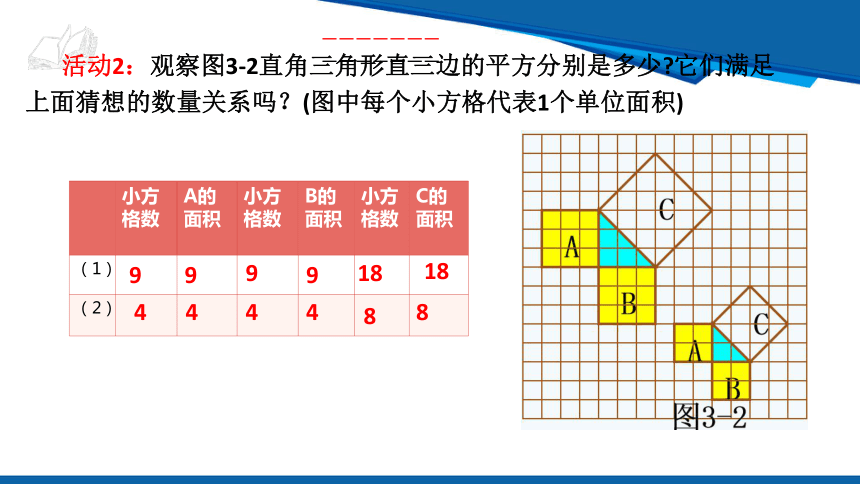
活动2:观察图3-2直角三角形直三边的平方分别是多少 它们满足上面猜想的数量关系吗?(图中每个小方格代表1个单位面积)
——————————————
小方格数 A的面积 小方格数 B的面积 小方格数 C的面积
(1)
(2)
9
9
9
9
18
4
4
4
4
8
18
8
直角边长的平方等于正方形的面积.
问题1:你发现A、B、C的面积之间有什么关系?
问题2:正方形的面积与直角边长的平方有什么关系?
活动3:图3-3中的直角三角形是否也具有这样的关系?你又是如何计算的?
A
B
C
A
B
C
小方格数 A的面积 小方格数 B的面积 小方格数 C的面积
(1)
(2)
16
16
9
9
25
25
1
1
9
9
10
10
(1)
(2)
你发现A、B、C的面积之间有什么关系?
发现+=.
如果直角三角形的两直角边长分别为1.6个单位和2.4个单位长度,那么上面所猜想的数量关系还成立吗?说明你的理由.
成立
活动4:
直角三角形两直角边的平方和等于斜边的平方.
勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么 .
即 .
数学表达式:
在Rt△ABC中,∠C=90°,
AB=c,AC=b,BC=a,则 .
总结:
a2+b2=c2
a2+b2=c2
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.因此,我国称上面的结论为勾股定理.
在西方,又称毕达哥拉斯定理!
典例精讲
例1在Rt△ABC中∠C=90°,∠A、∠B、∠C的对边分别为a、b、c.
(1)a=6,b=8,求c.
(2)b=40,c=41, 求a.
解:(1)因为=+=+=100,
所以c=10.
(2)因为+=,
所以=-=-=81,
所以a=9.
即时测评
1.如图是4×4方格中的一个阴影正方形,若每个小方格的边长是1,则该阴影正方形的边长为( )
A. B. C. D.
2.已知直角三角形的两条直角边的长分别为3,4,则斜边上的高为 .
D
3.如图,在△ABC中,BC=5,点D在BC上,且AD⊥BC,AD=BD=3,求AB,AC的长.
解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵AD=DB=3,BC=5,
∴CD=BC﹣BD=5﹣3=2,
∴AB==
AC=.
1.如果直角三角形的两条边长分别是3和4,则第三边的长是( )
A.7 B.5 C. D.5或
2.如图,Rt△ABC中,AC=6,BC=8,则其内部五个小直角三角形的周长之和为 .
D
24
3.如图,在四边形ABCD中,∠ABC=∠CDA=90°,分别以四边形ABCD的四条边为边长,向外作四个正方形,面积分别为S1,S2,S3,S4,若S1=8,S2=11,S3=15,则S4的值是 .
18
4.如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点D,若BC=6,AB=10.
(1)求AC的长;
解:(1)在Rt△ABC中,由勾股定理得:
AC==
(2)过点D作DE⊥AB,垂足为E,求DE的长
(2)如图,过点D作DE⊥AB于点E,
∵∠C=90°,BD是∠ABC的平分线,
∴DE=CD,
设CD=x,则DE=x,
∵S△ABC=S△ABD+S△BCD,
∴×6×8=×6CD+×10DE,
即24=3x+5x,
解得x=3,
即DE=3.
5.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O.
(1)若AO=2,BO=3,CO=4,DO=5,请求出AB2,BC2,CD2,DA2的值;
(2)若AB=6,CD=10,求BC2+AD2的值;
(3)请根据(1)(2)题中的信息,
写出关于“垂美”四边形关于边的一条结论.
解:(1)∵AC⊥BD,
∴△ABO是直角三角形,
∴AB2=AO2+BO2,
同理,可得:BC2=BO2+CO2,
CD2=CO2+DO2,AD2=AO2+DO2,
∵AO=2,BO=3,CO=4,DO=5,
∴AB2=13,BC2=25,CD2=41,AD2=29;
(2)由(1)得:
BC2+AD2=(BO2+CO2)+(AO2+DO2)
=(BO2+AO2)+(CO2+DO2)
=AB2+CD2,
即:BC2+AD2=AB2+CD2,
∵AB=6,CD=10,
∴BC2+AD2=62+102=136;
(3)结论:“垂美”四边形的两组对边的平方和相等.
勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为c,那么a + b = c
课堂小结:
基础题:1.课后习题第 3题
提高题:2.请学有余力的同学做第4题,下节课在班内展示、交流。
课后作业
本节课到此结束,
谢谢大家!
第三章 勾股定理
1 探索勾股定理
第1课时 探索勾股定理
学习目标
1.体验勾股定理的探索过程,由特例猜想勾股定理,再由特例验证勾股定理.
2.会利用勾股定理解释生活中的简单现象.
如图,从电线杆离地面8m处向地面拉一条钢索,如果这条钢索在地面的固定点距离电线杆底部6m,那么需要多长钢索?
课堂导入
创设情境引入新课
如图,从电线杆离地面8 m处向地面拉一条钢索,若这条钢索在地面的固定点距离电线杆底部6 m,那么需要多长的钢索
在直角三角形中,任意两条边确定了,另外一条边也就随之确定吗 三边之间存在着一个特定的数量关系.事实上,古人发现,直角三角形的三条边长度的平方存在着一个特殊的关系.
让我们一起去探索吧!
以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
活动1:在纸上作出若干个直角三角形,分别测量它们的三条边,看看三边长的平方之间有什么样的关系 与同伴交流.
[任务 探究勾股定理]
活动2:观察图3-2直角三角形直三边的平方分别是多少 它们满足上面猜想的数量关系吗?(图中每个小方格代表1个单位面积)
——————————————
小方格数 A的面积 小方格数 B的面积 小方格数 C的面积
(1)
(2)
9
9
9
9
18
4
4
4
4
8
18
8
直角边长的平方等于正方形的面积.
问题1:你发现A、B、C的面积之间有什么关系?
问题2:正方形的面积与直角边长的平方有什么关系?
活动3:图3-3中的直角三角形是否也具有这样的关系?你又是如何计算的?
A
B
C
A
B
C
小方格数 A的面积 小方格数 B的面积 小方格数 C的面积
(1)
(2)
16
16
9
9
25
25
1
1
9
9
10
10
(1)
(2)
你发现A、B、C的面积之间有什么关系?
发现+=.
如果直角三角形的两直角边长分别为1.6个单位和2.4个单位长度,那么上面所猜想的数量关系还成立吗?说明你的理由.
成立
活动4:
直角三角形两直角边的平方和等于斜边的平方.
勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么 .
即 .
数学表达式:
在Rt△ABC中,∠C=90°,
AB=c,AC=b,BC=a,则 .
总结:
a2+b2=c2
a2+b2=c2
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.因此,我国称上面的结论为勾股定理.
在西方,又称毕达哥拉斯定理!
典例精讲
例1在Rt△ABC中∠C=90°,∠A、∠B、∠C的对边分别为a、b、c.
(1)a=6,b=8,求c.
(2)b=40,c=41, 求a.
解:(1)因为=+=+=100,
所以c=10.
(2)因为+=,
所以=-=-=81,
所以a=9.
即时测评
1.如图是4×4方格中的一个阴影正方形,若每个小方格的边长是1,则该阴影正方形的边长为( )
A. B. C. D.
2.已知直角三角形的两条直角边的长分别为3,4,则斜边上的高为 .
D
3.如图,在△ABC中,BC=5,点D在BC上,且AD⊥BC,AD=BD=3,求AB,AC的长.
解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵AD=DB=3,BC=5,
∴CD=BC﹣BD=5﹣3=2,
∴AB==
AC=.
1.如果直角三角形的两条边长分别是3和4,则第三边的长是( )
A.7 B.5 C. D.5或
2.如图,Rt△ABC中,AC=6,BC=8,则其内部五个小直角三角形的周长之和为 .
D
24
3.如图,在四边形ABCD中,∠ABC=∠CDA=90°,分别以四边形ABCD的四条边为边长,向外作四个正方形,面积分别为S1,S2,S3,S4,若S1=8,S2=11,S3=15,则S4的值是 .
18
4.如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点D,若BC=6,AB=10.
(1)求AC的长;
解:(1)在Rt△ABC中,由勾股定理得:
AC==
(2)过点D作DE⊥AB,垂足为E,求DE的长
(2)如图,过点D作DE⊥AB于点E,
∵∠C=90°,BD是∠ABC的平分线,
∴DE=CD,
设CD=x,则DE=x,
∵S△ABC=S△ABD+S△BCD,
∴×6×8=×6CD+×10DE,
即24=3x+5x,
解得x=3,
即DE=3.
5.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O.
(1)若AO=2,BO=3,CO=4,DO=5,请求出AB2,BC2,CD2,DA2的值;
(2)若AB=6,CD=10,求BC2+AD2的值;
(3)请根据(1)(2)题中的信息,
写出关于“垂美”四边形关于边的一条结论.
解:(1)∵AC⊥BD,
∴△ABO是直角三角形,
∴AB2=AO2+BO2,
同理,可得:BC2=BO2+CO2,
CD2=CO2+DO2,AD2=AO2+DO2,
∵AO=2,BO=3,CO=4,DO=5,
∴AB2=13,BC2=25,CD2=41,AD2=29;
(2)由(1)得:
BC2+AD2=(BO2+CO2)+(AO2+DO2)
=(BO2+AO2)+(CO2+DO2)
=AB2+CD2,
即:BC2+AD2=AB2+CD2,
∵AB=6,CD=10,
∴BC2+AD2=62+102=136;
(3)结论:“垂美”四边形的两组对边的平方和相等.
勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为c,那么a + b = c
课堂小结:
基础题:1.课后习题第 3题
提高题:2.请学有余力的同学做第4题,下节课在班内展示、交流。
课后作业
本节课到此结束,
谢谢大家!
