3.1 探索勾股定理 第2课时 勾股定理的验证与应用 课件 (共31张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 3.1 探索勾股定理 第2课时 勾股定理的验证与应用 课件 (共31张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 00:00:00 | ||
图片预览





文档简介
(共31张PPT)
第三章 勾股定理
1 探索勾股定理
第2课时 勾股定理的验证与应用
1.理解并掌握验证勾股定理的多种方法。
2.通过对几种常见的勾股定理验证方法的分析和欣赏,理解数学知识之间的内在联系。
3.掌握运用勾股定理解决一些实际问题的方法。
学习目标
2002年世界数学家大会在我国北京召开,投影显示本届世界数学家大会的会标:会标中央的图案是一个与“勾股定理”有关的图形,它既标志着中国古代的数学成就,又像一只转动的风车,欢迎来自世界各地的数学家们!今天我们就来一同探索勾股定理的图形验证.
[任务一 探究拼图的方法验证勾股定理]
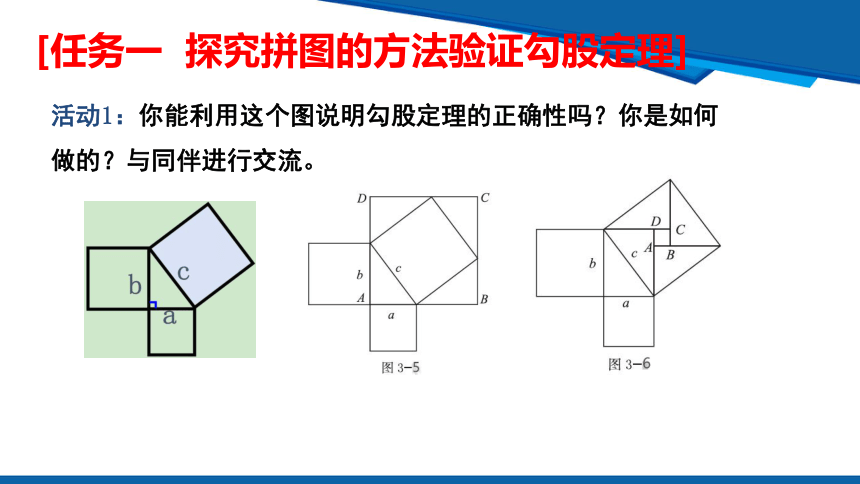
活动1:你能利用这个图说明勾股定理的正确性吗?你是如何做的?与同伴进行交流。
问题1 将图3-5、图3-6中所有三角形和正方形的面积用含a.b、c的式了表示出来.
为了方便计算图中大正方形的面积,对其进行适当割补:
图3-5、3-6中,三角形面积ab,正方形面积分别为.
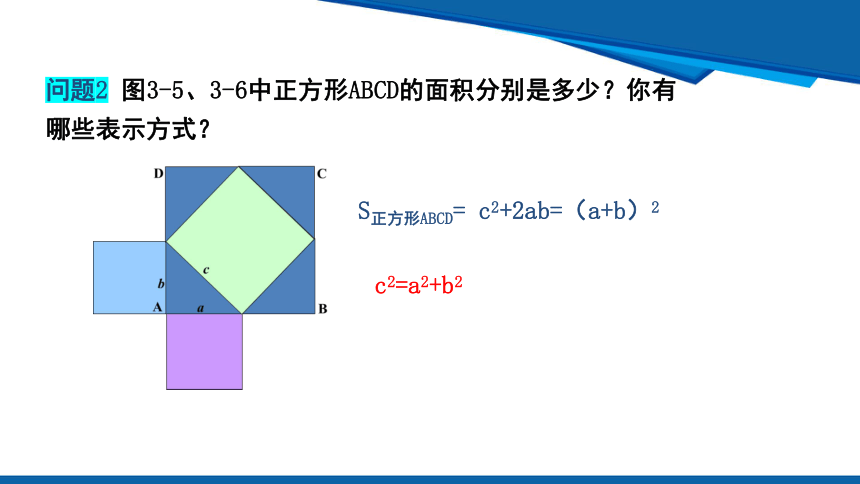
S正方形ABCD= c2+2ab=(a+b)2
c2=a2+b2
问题2 图3-5、3-6中正方形ABCD的面积分别是多少?你有哪些表示方式?
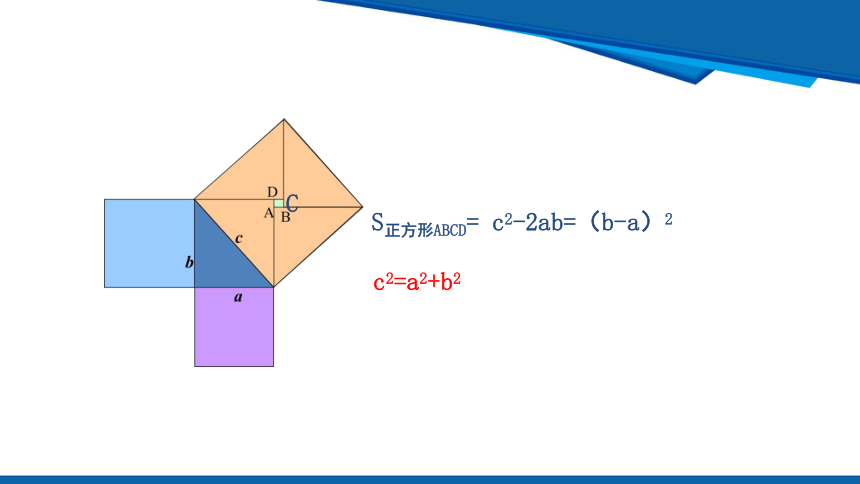
S正方形ABCD= c2-2ab=(b-a)2
c2=a2+b2
C
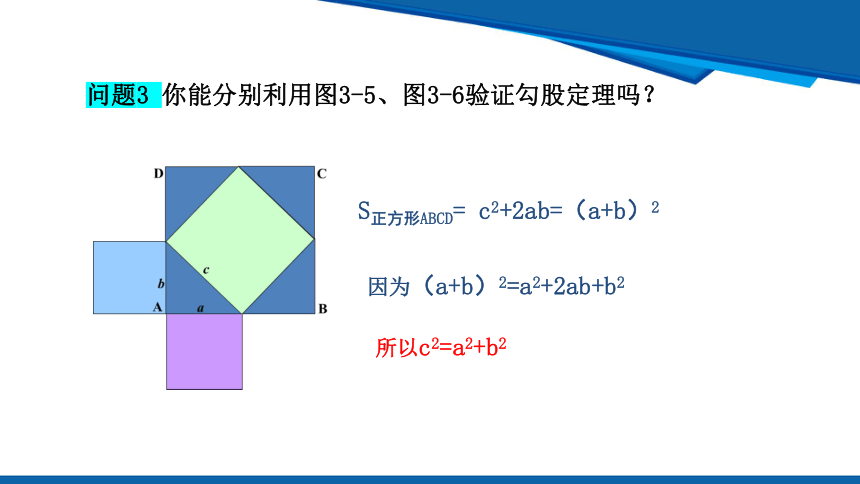
S正方形ABCD= c2+2ab=(a+b)2
所以c2=a2+b2
问题3 你能分别利用图3-5、图3-6验证勾股定理吗?
因为(a+b)2=a2+2ab+b2
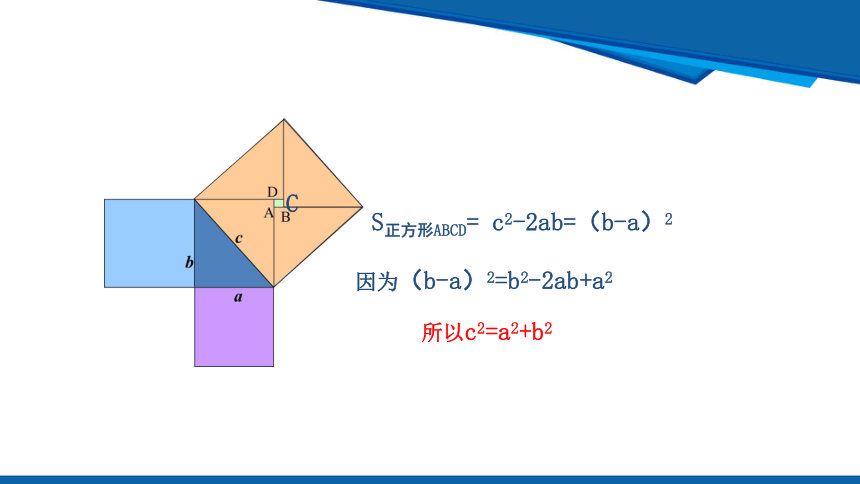
S正方形ABCD= c2-2ab=(b-a)2
所以c2=a2+b2
C
因为(b-a)2=b2-2ab+a2
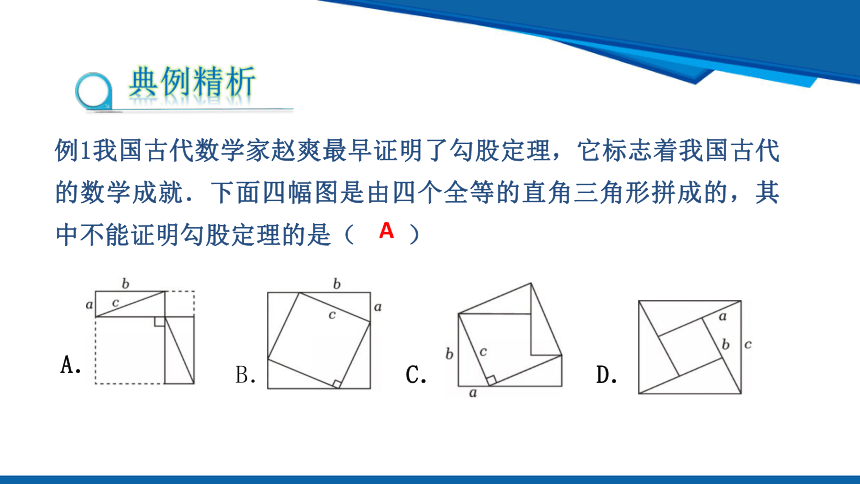
典例精析
例1我国古代数学家赵爽最早证明了勾股定理,它标志着我国古代的数学成就.下面四幅图是由四个全等的直角三角形拼成的,其中不能证明勾股定理的是( )
A.
B.
C.
D.
A
1.如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.如果直角三角形较长直角边的长为a,较短直角边的长为b,若ab=7,大正方形的面积为30,则小正方形的边长为( )
A.16 B.8 C.4 D.2
即时测评
C
2.如图,四个全等的直角三角形围成一个大正方形ABCD,中间阴影部分是一个小正方形EFGH,这样就组成一个“赵爽弦图”.若AB=10,AE=8,则正方形EFGH的面积为 .
4
典例精析
例2.我方侦察员小王在距离东西向公路 400 m 处侦察,发现一辆敌方汽车在公路上疾驶. 他赶紧拿出红外测距仪,测得汽车与他相距 400 m,10 s 后,汽车与他相距 500 m,你能帮小王计算敌方汽车的速度吗?
你能根据题意画出图形吗?在你画的图形中存在一个怎样的三角形?
解:其中点A表示王叔叔所直位置、点C、点B分别表示两个时刻蓝方汽车的位置。由于王叔叔距离公路400m,因此∠C是直角.
由勾股定理,可得到
AB2 = BC2 + AC2,
也就是5002 = BC2 + 4002,
所以BC = 300.
蓝方汽车 10 s 行驶了 300 m,那么它 1 s 行驶的距离为 300÷10 = 30 (m),即蓝方汽车这10s的平均速度为30m/s.
400 m
500 m
C
B
公路
A
1.如图,台风过后,某市体育中心附近一棵大树在高于地面3米处折断,大树顶部落在距离大树底部4米处的地面上.则这棵树折断之前的高度( )
A.7m B.8m C.9m D.10m
2.如图,湖的两岸有A、C两点,在与AC成直角的BC方向上的点C处测得AB=15米,BC=12米,则A、C两点间的距离为 米.
即时测评
B
9
3.某同学想运用所学知识测量一棵大树的高度AB,如图,他在地面上点C的正上方放置一个测距仪,测距仪位于点D处时,测得测距仪到树干的水平距离DE=7米,测距仪到大树顶端A的距离AD=25米,已知DE⊥AB于点E,CD=BE=1.6米,请你求出这棵大树的高度AB.
解:由勾股定理得:
AE===24,
∴大树的高度AB=AE+BE=24+1.6=25.6(米).
活动2:如果一个三角形是钝角三角形或锐角三角形,那么它的三边长仍然满足“较长边的平方等于另外两边的平方和”吗?
说说你的判断和理由,并与同伴进行交流.
b
a
c
b
a
c
[任务三 探究非直角三角形的三边关系]
①在钝角三角形中,三边长分别为a,b,c,其中 c 为最大边长,
则 a2 + b2 < c2;
b
a
c
b
a
c
②在锐角三角形中,
三边长分别为a,b,c,其中 c 为最大边长,
则 a2 + b2 > c2.
S = 9
S = 25
S = 10
S = 9
S = 10
S = 13
1.在学习勾股定理时,甲同学用四个相同的直角三角形(直角边长分别为a,b,斜边长为c)构成如图所示的正方形;乙同学用边长分别为a,b的两个正方形和长为b,宽为a的两个长方形构成如图所示的正方形,甲、乙两位同学给出的构图方案,可以证明勾股定理的是( )
A.甲 B.乙
C.甲,乙都可以 D.甲,乙都不可以
A
2. 放学以后,小红和小颖从学校分手,分别沿着东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为( )
A. 600米 B. 800米 C. 1000米 D 不能确定
C
3.如图,王大爷准备建一个蔬菜大棚,棚宽8m,高6m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,阳光透过的最大面积是_______.
200m2
4.如图,笔直的公路上 A,B 两点相距 25 km,C,D 为两村庄,DA ⊥ AB 于点 A,CB⊥ AB 于点 B,已知 DA = 15 km,
CB = 10 km,现在要在公路的 AB 段上建一个土特产品收购
站 E,使得 C,D 两村到收购站 E 的距离相等,则收购站 E 应建在离 A 点多远处?
解:因为DA⊥AB 于点 A,CB⊥AB 于点 B,所以∠A=∠B=90°,所以 AE2+AD2=DE2 ,BE2+BC2=EC2 .
由题意可知 DE=EC,所以 AE2 +AD2=BE2+BC2 .
设 AE=x km,则 BE=AB-AE=(25-x) km.
因为 DA=15 km,CB=10 km,
所以 x2 +152=(25-x)2+102 ,
解得 x=10,所以 AE=10 km.
所以收购站 E 应建在离 A 点 10 km 处.
5.用四个全等的直角三角形拼成如图①所示的大正方形,中间也是一个正方形,它是美丽的弦图,其中四个直角三角形的直角边长分别为a,b(a<b),斜边长为c.
(1)请利用图①证明:a2+b2=c2;
(2)如图②,将这四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH,若该图形的周长为80,OB=5,求该图形的面积.
5.(1)证明:S小正方形=(b﹣a)2=a2﹣2ab+b2,
S小正方形=c2﹣4ab=c2﹣2ab,
即b2﹣2ab+a2=c2﹣2ab,
∴a2+b2=c2;
(2)解:∵AB+BC=80÷4=20,
设AH=BC=x,则AB=20﹣x,OH=OB=5,
在Rt△AOB中,由勾股定理得:OH2+OG2=GH2
即52+(5+x)2=(20-x)2,
解得:x=7,
∴S=×5×12×4=120.
勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为c,那么a + b = c
课堂小结:
基础题:1.课后习题第 1题
提高题:2.请学有余力的同学做课后习题第 4题,下节课在班内展示。
课后作业
本节课到此结束,
谢谢大家!
第三章 勾股定理
1 探索勾股定理
第2课时 勾股定理的验证与应用
1.理解并掌握验证勾股定理的多种方法。
2.通过对几种常见的勾股定理验证方法的分析和欣赏,理解数学知识之间的内在联系。
3.掌握运用勾股定理解决一些实际问题的方法。
学习目标
2002年世界数学家大会在我国北京召开,投影显示本届世界数学家大会的会标:会标中央的图案是一个与“勾股定理”有关的图形,它既标志着中国古代的数学成就,又像一只转动的风车,欢迎来自世界各地的数学家们!今天我们就来一同探索勾股定理的图形验证.
[任务一 探究拼图的方法验证勾股定理]
活动1:你能利用这个图说明勾股定理的正确性吗?你是如何做的?与同伴进行交流。
问题1 将图3-5、图3-6中所有三角形和正方形的面积用含a.b、c的式了表示出来.
为了方便计算图中大正方形的面积,对其进行适当割补:
图3-5、3-6中,三角形面积ab,正方形面积分别为.
S正方形ABCD= c2+2ab=(a+b)2
c2=a2+b2
问题2 图3-5、3-6中正方形ABCD的面积分别是多少?你有哪些表示方式?
S正方形ABCD= c2-2ab=(b-a)2
c2=a2+b2
C
S正方形ABCD= c2+2ab=(a+b)2
所以c2=a2+b2
问题3 你能分别利用图3-5、图3-6验证勾股定理吗?
因为(a+b)2=a2+2ab+b2
S正方形ABCD= c2-2ab=(b-a)2
所以c2=a2+b2
C
因为(b-a)2=b2-2ab+a2
典例精析
例1我国古代数学家赵爽最早证明了勾股定理,它标志着我国古代的数学成就.下面四幅图是由四个全等的直角三角形拼成的,其中不能证明勾股定理的是( )
A.
B.
C.
D.
A
1.如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.如果直角三角形较长直角边的长为a,较短直角边的长为b,若ab=7,大正方形的面积为30,则小正方形的边长为( )
A.16 B.8 C.4 D.2
即时测评
C
2.如图,四个全等的直角三角形围成一个大正方形ABCD,中间阴影部分是一个小正方形EFGH,这样就组成一个“赵爽弦图”.若AB=10,AE=8,则正方形EFGH的面积为 .
4
典例精析
例2.我方侦察员小王在距离东西向公路 400 m 处侦察,发现一辆敌方汽车在公路上疾驶. 他赶紧拿出红外测距仪,测得汽车与他相距 400 m,10 s 后,汽车与他相距 500 m,你能帮小王计算敌方汽车的速度吗?
你能根据题意画出图形吗?在你画的图形中存在一个怎样的三角形?
解:其中点A表示王叔叔所直位置、点C、点B分别表示两个时刻蓝方汽车的位置。由于王叔叔距离公路400m,因此∠C是直角.
由勾股定理,可得到
AB2 = BC2 + AC2,
也就是5002 = BC2 + 4002,
所以BC = 300.
蓝方汽车 10 s 行驶了 300 m,那么它 1 s 行驶的距离为 300÷10 = 30 (m),即蓝方汽车这10s的平均速度为30m/s.
400 m
500 m
C
B
公路
A
1.如图,台风过后,某市体育中心附近一棵大树在高于地面3米处折断,大树顶部落在距离大树底部4米处的地面上.则这棵树折断之前的高度( )
A.7m B.8m C.9m D.10m
2.如图,湖的两岸有A、C两点,在与AC成直角的BC方向上的点C处测得AB=15米,BC=12米,则A、C两点间的距离为 米.
即时测评
B
9
3.某同学想运用所学知识测量一棵大树的高度AB,如图,他在地面上点C的正上方放置一个测距仪,测距仪位于点D处时,测得测距仪到树干的水平距离DE=7米,测距仪到大树顶端A的距离AD=25米,已知DE⊥AB于点E,CD=BE=1.6米,请你求出这棵大树的高度AB.
解:由勾股定理得:
AE===24,
∴大树的高度AB=AE+BE=24+1.6=25.6(米).
活动2:如果一个三角形是钝角三角形或锐角三角形,那么它的三边长仍然满足“较长边的平方等于另外两边的平方和”吗?
说说你的判断和理由,并与同伴进行交流.
b
a
c
b
a
c
[任务三 探究非直角三角形的三边关系]
①在钝角三角形中,三边长分别为a,b,c,其中 c 为最大边长,
则 a2 + b2 < c2;
b
a
c
b
a
c
②在锐角三角形中,
三边长分别为a,b,c,其中 c 为最大边长,
则 a2 + b2 > c2.
S = 9
S = 25
S = 10
S = 9
S = 10
S = 13
1.在学习勾股定理时,甲同学用四个相同的直角三角形(直角边长分别为a,b,斜边长为c)构成如图所示的正方形;乙同学用边长分别为a,b的两个正方形和长为b,宽为a的两个长方形构成如图所示的正方形,甲、乙两位同学给出的构图方案,可以证明勾股定理的是( )
A.甲 B.乙
C.甲,乙都可以 D.甲,乙都不可以
A
2. 放学以后,小红和小颖从学校分手,分别沿着东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为( )
A. 600米 B. 800米 C. 1000米 D 不能确定
C
3.如图,王大爷准备建一个蔬菜大棚,棚宽8m,高6m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,阳光透过的最大面积是_______.
200m2
4.如图,笔直的公路上 A,B 两点相距 25 km,C,D 为两村庄,DA ⊥ AB 于点 A,CB⊥ AB 于点 B,已知 DA = 15 km,
CB = 10 km,现在要在公路的 AB 段上建一个土特产品收购
站 E,使得 C,D 两村到收购站 E 的距离相等,则收购站 E 应建在离 A 点多远处?
解:因为DA⊥AB 于点 A,CB⊥AB 于点 B,所以∠A=∠B=90°,所以 AE2+AD2=DE2 ,BE2+BC2=EC2 .
由题意可知 DE=EC,所以 AE2 +AD2=BE2+BC2 .
设 AE=x km,则 BE=AB-AE=(25-x) km.
因为 DA=15 km,CB=10 km,
所以 x2 +152=(25-x)2+102 ,
解得 x=10,所以 AE=10 km.
所以收购站 E 应建在离 A 点 10 km 处.
5.用四个全等的直角三角形拼成如图①所示的大正方形,中间也是一个正方形,它是美丽的弦图,其中四个直角三角形的直角边长分别为a,b(a<b),斜边长为c.
(1)请利用图①证明:a2+b2=c2;
(2)如图②,将这四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH,若该图形的周长为80,OB=5,求该图形的面积.
5.(1)证明:S小正方形=(b﹣a)2=a2﹣2ab+b2,
S小正方形=c2﹣4ab=c2﹣2ab,
即b2﹣2ab+a2=c2﹣2ab,
∴a2+b2=c2;
(2)解:∵AB+BC=80÷4=20,
设AH=BC=x,则AB=20﹣x,OH=OB=5,
在Rt△AOB中,由勾股定理得:OH2+OG2=GH2
即52+(5+x)2=(20-x)2,
解得:x=7,
∴S=×5×12×4=120.
勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为c,那么a + b = c
课堂小结:
基础题:1.课后习题第 1题
提高题:2.请学有余力的同学做课后习题第 4题,下节课在班内展示。
课后作业
本节课到此结束,
谢谢大家!
