3.2 一定是直角三角形吗(共28张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 3.2 一定是直角三角形吗(共28张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 10:41:31 | ||
图片预览






文档简介
(共28张PPT)
第三章 勾股定理
2 一定是直角三角形吗
学习目标
1.掌握直角三角形的判别条件,并能进行简单应用.
2.能够识别勾股数并运用勾股数解决简单实际问题,培养从实际问题抽象出数学问题的能力.
3.通过由边长判断三角形是否是直角三角形的过程,理解“探究—归纳—验证”的数学思想.
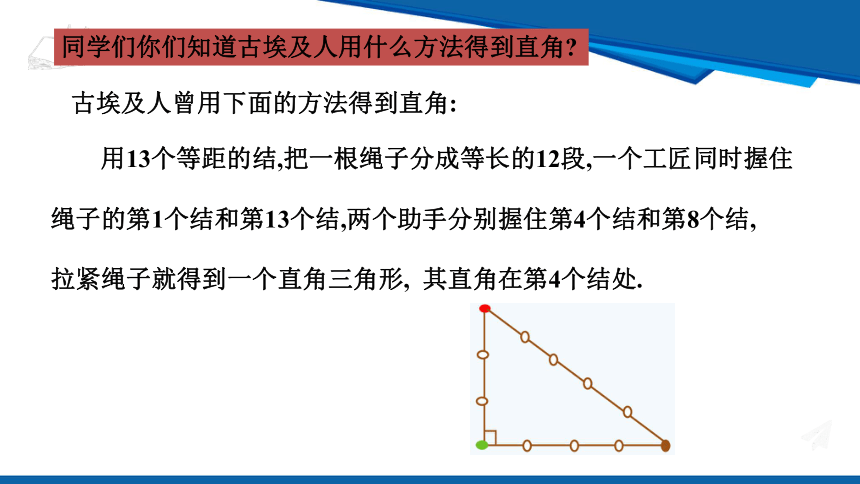
同学们你们知道古埃及人用什么方法得到直角
古埃及人曾用下面的方法得到直角:
用13个等距的结,把一根绳子分成等长的12段,一个工匠同时握住
绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,
拉紧绳子就得到一个直角三角形, 其直角在第4个结处.
下列的三组数分别是一个三角形的三边长a,b,c:
① 5,12,13; ② 7,24,25;
③ 8,15,17
问题1:这三组数都满足a2+b2=c2吗?
(2)分别以每组数为三边作出三角形,用量角器量一量,它们都是直角三角形吗?
合作交流探究新知
满足
是直角三角形
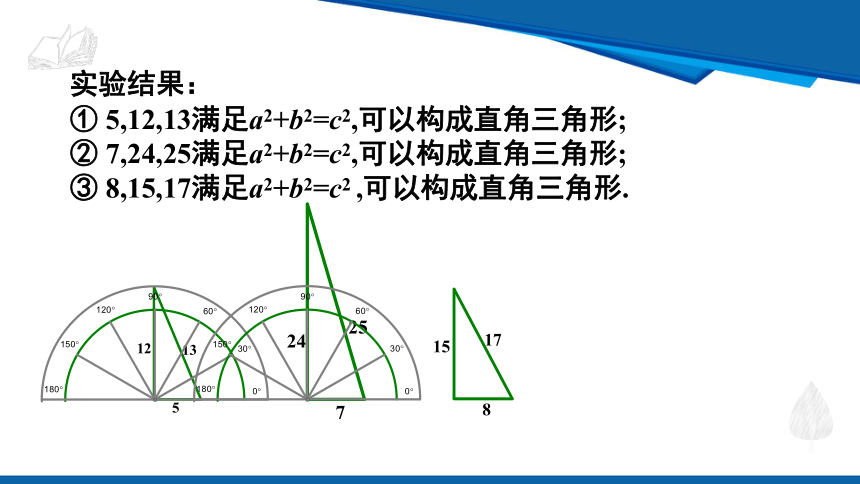
实验结果:
① 5,12,13满足a2+b2=c2,可以构成直角三角形;
② 7,24,25满足a2+b2=c2,可以构成直角三角形;
③ 8,15,17满足a2+b2=c2 ,可以构成直角三角形.
问题3:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形。
满足a2+b2=c2的三个正整数,称为勾股定理.
例1 一个零件的形状如图1所示,按规定这个零件中,∠A和∠DBC都应为直角,工人师傅量得这个零件各边尺寸如图2所示,这个零件符合要求吗?
A
B
C
D
A
B
C
D
图1
图2
解:∵在Rt△ABD中,AB2+AD2=9+16=25=BD2
∴△ABD是直角三角形,∠A是直角
∵在△BCD中,BD2+BC2=25+144=169=CD2
∴△BCD是直角三角形,∠DBC是直角
因此这个零件符合要求
3
4
13
12
5
典例精讲
1.下列每组数表示三条线段长,其中可以构成直角三角形的一组线段是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
2.由下列条件不能判断△ABC是直角三角形的是( )
A.AB:BC:AC=6:8:10 B.∠A:∠B:∠C=3:4:5
C.∠A=∠B﹣∠C D.AB2=BC2﹣AC2
c
B
即时测评
3.某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角建造了一块绿化地(阴影部分).如图,已知AB=9m,BC=12m,CD=17m,AD=8m,技术人员通过测量确定了∠ABC=90°.则这片绿地的面积是 m2.
114
4.如图,方格纸中小正方形的边长为1个单位长度,△ABC为格点三角形.请判断△ABC的形状,并说明理由.
解:△ABC是直角三角形,
理由:由题意得:AC2=42+22=20,
AB2=42+32=25,
BC2=12+22=5,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
如果一个三角形的三边长,满足a2+b2=c2,那么这个三角形是直角三角形。
满足a2+b2=c2的三个正整数,称为勾股数.
[任务二 探究勾股数]
如果将直角三角形的三条边长同时扩大一个相同的倍数,得到的三角形还是直角三角形吗?填写下表,并验证你所填的数是否满足“勾股数”.
思考?
2倍 3倍
3,4,5 6,8,10
5,12,13 15,36,39
8,15,17
7,24,25
9,40,41
9,12,15
24,45,51
21,72,75
27,120,123
18,80,82
14,48,50
16,30,34
10,24,26
例2 下列各组数是勾股数的是( )
A.13,14,15 B.3,4,5
C.0.3,0.4,0.5 D.6,8,11
图1
图2
典例精讲
B
1.下列各组数中,是“勾股数”的一组是( )
A.4,5,6 B.1.5,2,2.5 C.6,8,10 D.1,,2
2.下列各组数为勾股数的是 (填序号).
①1.5,2,3;②3,4,7;③7,12,13;
④8,15,17;⑤9,40,41.
图1
图2
即时测评
C
④⑤
3.观察以下几组勾股数,并寻找规律:
①3,4,5;
②5,12,13;
③7,24,25;
④9,40,41;
,
请你写出具有以上规律的第⑦组勾股数: .
图1
图2
15,112,113
2. 五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是( )
1. 下列各组数中,以a,b,c为边的三角形不是直角三角形的是( )
A.a=1.5,b=2,c=3 B.a=7,b=24,c=25
C.a=6,b=8,c=10 D.a=3,b=4,c=5
A
C
A B C D
3. 一个三角形三边长的比为3:4:5,它的周长是24cm,这个三角形的面积为 cm2.
4. 已知|x﹣12|+(y﹣13)2与z2﹣10z+25互为相反数,则以x,y,z为边的三角形是 三角形.
24
直角
5.如图,在四边形ABCD中,∠B=90°,AB=BC=4,CD=6,DA=2.求∠DAB的度数.
解:∵∠B=90°,AB=BC=4,
∴AC===,
∠DAB=∠DBA=45°,
∵()2+22=62,
∴AC2+DA2=CD2,
∴△ACD是直角三角形,
∵∠DAC是CD所对的角,
∴∠DAC=90°,
∴∠DAB=∠DAC+∠BAC=90°+45°=135°.
6.如图,在△ABC中,AB=AC,D是AC边上一点,连接BD,已知BC=15,CD=9,BD=12.
(1)判断△BCD的形状,并说明理由.
(2)求AD的长.
解:(1)△ABD是直角三角形,
理由:在△CBD中,BC=15.CD=9,BD=12,
∵==225,==225,
∴,
∴△BCD是直角三角形,且∠BDC=90°,
∴△ABD是直角三角形;
(2)∵CD=9,
∴设AD=x,则AC=x+9,
∵AB=AC,
∴AB=x+9,
在Rt△ABD中, ,
∴ ,
∴x= .
1、 如果三角形三条边长分别为a,b,c ,那么满足a2+b2=c2 ,那么这个三角形是直角三角形
2、勾股定理判定的应用
课堂小结:
基础题:1.课后随堂练习第 2题
提高题:2.请学有余力的同学做习题第2题,下节课在班内展示、交流。
课后作业
本节课到此结束,
谢谢大家!
第三章 勾股定理
2 一定是直角三角形吗
学习目标
1.掌握直角三角形的判别条件,并能进行简单应用.
2.能够识别勾股数并运用勾股数解决简单实际问题,培养从实际问题抽象出数学问题的能力.
3.通过由边长判断三角形是否是直角三角形的过程,理解“探究—归纳—验证”的数学思想.
同学们你们知道古埃及人用什么方法得到直角
古埃及人曾用下面的方法得到直角:
用13个等距的结,把一根绳子分成等长的12段,一个工匠同时握住
绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,
拉紧绳子就得到一个直角三角形, 其直角在第4个结处.
下列的三组数分别是一个三角形的三边长a,b,c:
① 5,12,13; ② 7,24,25;
③ 8,15,17
问题1:这三组数都满足a2+b2=c2吗?
(2)分别以每组数为三边作出三角形,用量角器量一量,它们都是直角三角形吗?
合作交流探究新知
满足
是直角三角形
实验结果:
① 5,12,13满足a2+b2=c2,可以构成直角三角形;
② 7,24,25满足a2+b2=c2,可以构成直角三角形;
③ 8,15,17满足a2+b2=c2 ,可以构成直角三角形.
问题3:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形。
满足a2+b2=c2的三个正整数,称为勾股定理.
例1 一个零件的形状如图1所示,按规定这个零件中,∠A和∠DBC都应为直角,工人师傅量得这个零件各边尺寸如图2所示,这个零件符合要求吗?
A
B
C
D
A
B
C
D
图1
图2
解:∵在Rt△ABD中,AB2+AD2=9+16=25=BD2
∴△ABD是直角三角形,∠A是直角
∵在△BCD中,BD2+BC2=25+144=169=CD2
∴△BCD是直角三角形,∠DBC是直角
因此这个零件符合要求
3
4
13
12
5
典例精讲
1.下列每组数表示三条线段长,其中可以构成直角三角形的一组线段是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
2.由下列条件不能判断△ABC是直角三角形的是( )
A.AB:BC:AC=6:8:10 B.∠A:∠B:∠C=3:4:5
C.∠A=∠B﹣∠C D.AB2=BC2﹣AC2
c
B
即时测评
3.某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角建造了一块绿化地(阴影部分).如图,已知AB=9m,BC=12m,CD=17m,AD=8m,技术人员通过测量确定了∠ABC=90°.则这片绿地的面积是 m2.
114
4.如图,方格纸中小正方形的边长为1个单位长度,△ABC为格点三角形.请判断△ABC的形状,并说明理由.
解:△ABC是直角三角形,
理由:由题意得:AC2=42+22=20,
AB2=42+32=25,
BC2=12+22=5,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
如果一个三角形的三边长,满足a2+b2=c2,那么这个三角形是直角三角形。
满足a2+b2=c2的三个正整数,称为勾股数.
[任务二 探究勾股数]
如果将直角三角形的三条边长同时扩大一个相同的倍数,得到的三角形还是直角三角形吗?填写下表,并验证你所填的数是否满足“勾股数”.
思考?
2倍 3倍
3,4,5 6,8,10
5,12,13 15,36,39
8,15,17
7,24,25
9,40,41
9,12,15
24,45,51
21,72,75
27,120,123
18,80,82
14,48,50
16,30,34
10,24,26
例2 下列各组数是勾股数的是( )
A.13,14,15 B.3,4,5
C.0.3,0.4,0.5 D.6,8,11
图1
图2
典例精讲
B
1.下列各组数中,是“勾股数”的一组是( )
A.4,5,6 B.1.5,2,2.5 C.6,8,10 D.1,,2
2.下列各组数为勾股数的是 (填序号).
①1.5,2,3;②3,4,7;③7,12,13;
④8,15,17;⑤9,40,41.
图1
图2
即时测评
C
④⑤
3.观察以下几组勾股数,并寻找规律:
①3,4,5;
②5,12,13;
③7,24,25;
④9,40,41;
,
请你写出具有以上规律的第⑦组勾股数: .
图1
图2
15,112,113
2. 五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是( )
1. 下列各组数中,以a,b,c为边的三角形不是直角三角形的是( )
A.a=1.5,b=2,c=3 B.a=7,b=24,c=25
C.a=6,b=8,c=10 D.a=3,b=4,c=5
A
C
A B C D
3. 一个三角形三边长的比为3:4:5,它的周长是24cm,这个三角形的面积为 cm2.
4. 已知|x﹣12|+(y﹣13)2与z2﹣10z+25互为相反数,则以x,y,z为边的三角形是 三角形.
24
直角
5.如图,在四边形ABCD中,∠B=90°,AB=BC=4,CD=6,DA=2.求∠DAB的度数.
解:∵∠B=90°,AB=BC=4,
∴AC===,
∠DAB=∠DBA=45°,
∵()2+22=62,
∴AC2+DA2=CD2,
∴△ACD是直角三角形,
∵∠DAC是CD所对的角,
∴∠DAC=90°,
∴∠DAB=∠DAC+∠BAC=90°+45°=135°.
6.如图,在△ABC中,AB=AC,D是AC边上一点,连接BD,已知BC=15,CD=9,BD=12.
(1)判断△BCD的形状,并说明理由.
(2)求AD的长.
解:(1)△ABD是直角三角形,
理由:在△CBD中,BC=15.CD=9,BD=12,
∵==225,==225,
∴,
∴△BCD是直角三角形,且∠BDC=90°,
∴△ABD是直角三角形;
(2)∵CD=9,
∴设AD=x,则AC=x+9,
∵AB=AC,
∴AB=x+9,
在Rt△ABD中, ,
∴ ,
∴x= .
1、 如果三角形三条边长分别为a,b,c ,那么满足a2+b2=c2 ,那么这个三角形是直角三角形
2、勾股定理判定的应用
课堂小结:
基础题:1.课后随堂练习第 2题
提高题:2.请学有余力的同学做习题第2题,下节课在班内展示、交流。
课后作业
本节课到此结束,
谢谢大家!
