3.3 勾股定理的应用举例第1课时(共32张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 3.3 勾股定理的应用举例第1课时(共32张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 00:00:00 | ||
图片预览







文档简介
(共32张PPT)
第三章 勾股定理
3 勾股定理的应用举例
第1课时 勾股定理的实际应用(一)
学习目标
1.能运用勾股定理解决几何体表面两点间的最近距离问题
2.会利用勾股定理的逆定理验证垂直关系.
香肠放在B处,小狗从A点跑到B点,怎么跑最近?
有一个圆柱,它的高等于12厘米,底面上圆的半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少 (π的值取3)
A
B
C
我怎么走
会最近呢
任务一 探究圆柱体表面两点间的最近距离
活动1:
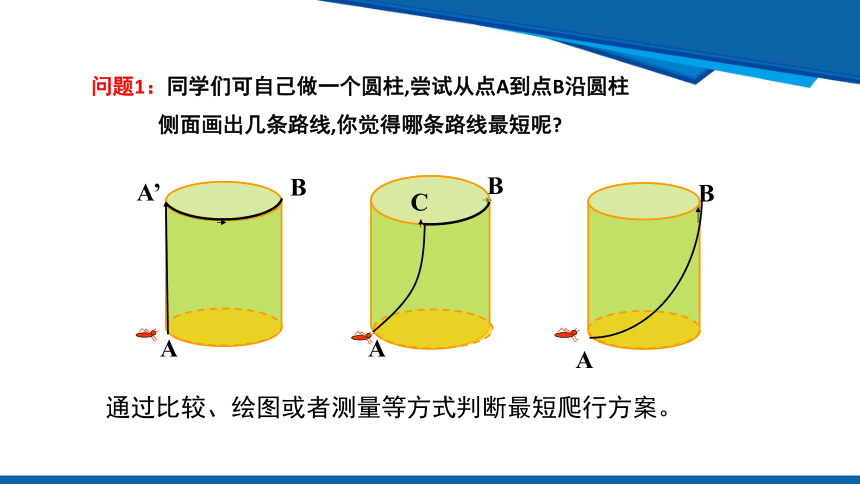
问题1:同学们可自己做一个圆柱,尝试从点A到点B沿圆柱侧面画出几条路线,你觉得哪条路线最短呢
A
B
A’
A
B
B
A
C
通过比较、绘图或者测量等方式判断最短爬行方案。
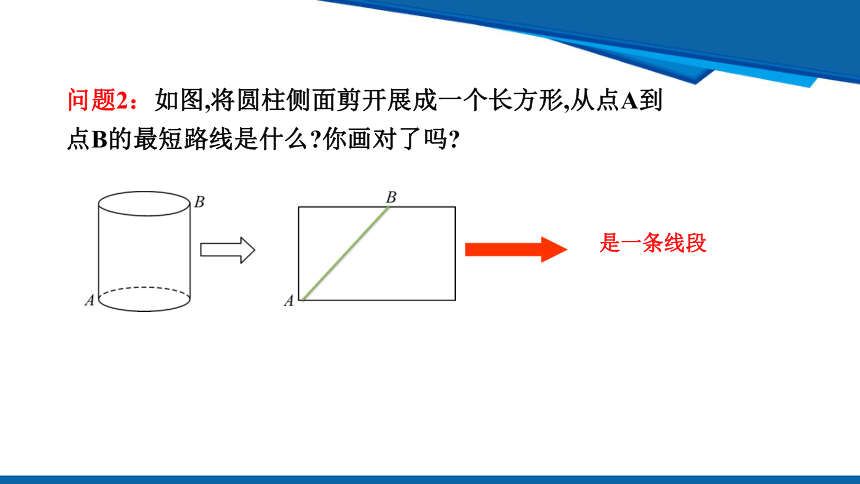
问题2:如图,将圆柱侧面剪开展成一个长方形,从点A到点B的最短路线是什么 你画对了吗
是一条线段
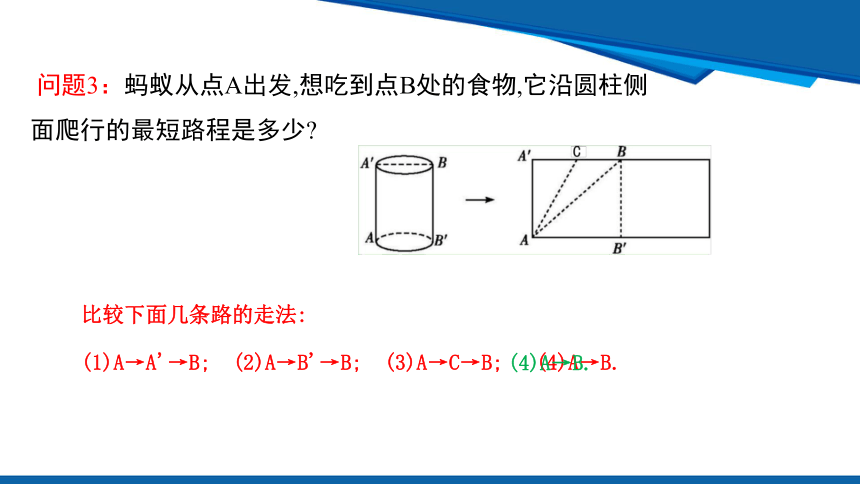
问题3:蚂蚁从点A出发,想吃到点B处的食物,它沿圆柱侧面爬行的最短路程是多少
比较下面几条路的走法:
(1)A→A'→B; (2)A→B'→B; (3)A→C→B; (4)A→B.
(4)A→B.
总结
确定圆柱上的最短路线:
求圆柱上两点之间的最短距离,可转化为求一个平面图形上对应线段的长.
其一般步骤:
(1)将圆柱的侧面展开为一个长方形;
(2)确定相应点的位置;
(3)连接相应点,构造直角三角形;
(4)利用勾股定理求解.
典例精析
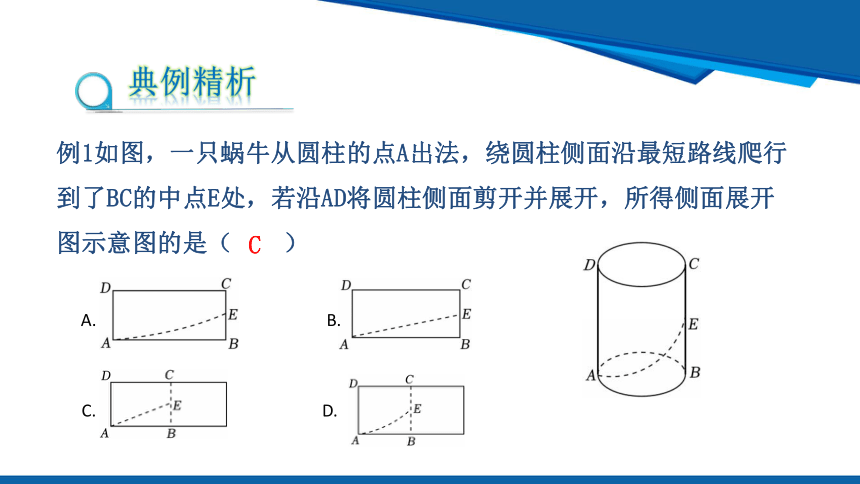
例1如图,一只蜗牛从圆柱的点A出法,绕圆柱侧面沿最短路线爬行到了BC的中点E处,若沿AD将圆柱侧面剪开并展开,所得侧面展开图示意图的是( )
C
A. B.
C. D.
即时测评
1.直四棱柱的上下底面是正方形,底面边长为5,高AB为9.在其侧面从点A开始,绕侧面两周,嵌入装饰彩条至点B停止,则彩条的最短长度为( )
A.41 B.50 C.9 D.29
A
2.如图,正方体的棱长为2cm,A是正方体的一个顶点,B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径是 cm.
3.如图,一只蚂蚁从点A沿圆柱表面爬到点B,圆柱高为15cm,底面半径为,蚂蚁爬行的最短路线长为多少?
解:展开之后如图,此时AB的长度即为最短路线长,
此时AC=×2π×=8(cm),BC=15cm,
∴AB===17(cm),
答:蚂蚁爬行的最短路线长为17cm.
装修工人李叔叔想要检测某块装修用砖的边AD和边BC是否分别垂直于底边AB。
该怎么测呢
[任务二 探究勾股定理逆定理的应用]
活动2:
问题1:如果例叔叔只带了卷尺,那么你能替他想办法完成任务吗
利用勾股定理的逆定理,分别量出AB、BC、AC 、AD的长.如果AB2+BC2=AC2,AB2+AD2=BD2,可得AD和BC分别垂直于底边AB.
问题2:李叔叔量得边AD长是30 cm,边AB长是40 cm,点B,D之间的距离是50 cm.边AD垂直于边AB吗
因为AD2+AB2=302+402=502= BD2,所以△ABD是直角三角形,
所以∠DAB = 90°,即 AD 边垂直于 AB 边.
问题3:如果李叔叔随身只有一个长度为20 cm的刻度尺,那么他能检验边AD是否垂直于边AB吗
例如:在AD 上取点 M,使 AM = 9 cm,在 AB 上取点 N 使 AN = 12 cm,测量MN 是否为 15 cm,若是,就垂直;若不是,就不垂直.
例2图①是某品牌婴儿车,图②是其部分结构示意图.根据安全标准需满足AB⊥BC,现量得AB=60cm,BC=45cm,AC=75cm,请通过计算说明该车是否符合安全标准.
典例精析
解:该车符合安全标准,理由如下:
∵AB=60,BC=45,AC=75,
∴
∵=5625,
∴,
∴△ABC是直角三角形,且∠ACB=90°,
∴AB⊥BC,
∴该车符合安全标准.
即时测评
1.如图,甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B.若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向是 .
北偏西60°
2.如图,某小区有一块四边形空地ABCD,连AC,经过测量可得△ABC是等腰三角形,AB=AC=15m,BC=18m,CD=8m,AD=17m.
(1)判断△ACD的形状;
(2)求这块空地的面积.
解:(1)∵AC=15,CD=8,AD=17,
∴
=289,
∴,
∴△ACD是直角三角形,∠ACD=90°;
(2)过点A作AH⊥BC于H,
∵AB=AC=15m,BC=18m,
∴BH=CH=9m,
在Rt△ABH中,AH===12m.
∴S△ABC+S△ACD=BC AH+AC CD
=×18×12+×15×8
=168().
答:这块空地的面积为168.
1.如图,一只蚂蚁从棱长为1的正方体纸箱的A点沿纸箱表面爬到B点,那么它所爬行的最短路线的长是( )
A. B. C. D.2
2.如图,已知圆柱底面的周长为12cm,圆柱高为8cm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为 .
C
20cm
3.如图所示,地面上铺了一块长方形地毯ABCD,因使用时间长而变形,中间形成一个半圆柱的凸起,半圆柱的底面直径为,已知AE+BF=20m,BC=10m,一只蚂蚁从A点爬到C点,且必须翻过半圆柱凸起,则它至少要走 m的路程.
26
4.如图一个三级台阶,它的每一级的长宽高分别是5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,点A上有一只蚂蚁,想到点B去吃可口的食物,则蚂蚁沿着台阶面爬到点B的最短路程长是多少?
解:如图所示,
∵三级台阶平面展开图为长方形,宽为5cm,
长为(3+1)×3=12(cm),
∴蚂蚁沿台阶面爬行到B点最短路程是AB的长,
由勾股定理得AB==13(cm),
答:蚂蚁沿着台阶面爬到B点最短路程是13cm.
5.某村有如图所示的一笔直公路AB,水源C处与公路之间有小片沼泽地,为方便公路上的人用水,拟从C处铺设水管到公路上.已知AB=200米,AC=160米,BC=120米.
(1)求∠ACB的大小;
(2)求铺设水管的最小长度.
解:(1)在△ABC中,AB=200米,AC=160米,BC=120米,
∵==40000,
∴,∴△ABC是直角三角形,
∴∠ACB=90°;
(2)当CD⊥AB时,铺设水管的长度最小,
∵△ABC的面积AB CD=AC BC,
∴AB CD=AC BC,∴200CD=120×160,
解得:CD=96,
∴铺设水管的最小长度为96米.
能说说运用勾股定理的知识可以解决实际生活中哪些问题
课堂小结:
基础题:1.课后练习第 1题
提高题:2.请学有余力的同学做课后习题第3题,并在下节课在班内展示、交流。
课后作业
本节课到此结束,
谢谢大家!
第三章 勾股定理
3 勾股定理的应用举例
第1课时 勾股定理的实际应用(一)
学习目标
1.能运用勾股定理解决几何体表面两点间的最近距离问题
2.会利用勾股定理的逆定理验证垂直关系.
香肠放在B处,小狗从A点跑到B点,怎么跑最近?
有一个圆柱,它的高等于12厘米,底面上圆的半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少 (π的值取3)
A
B
C
我怎么走
会最近呢
任务一 探究圆柱体表面两点间的最近距离
活动1:
问题1:同学们可自己做一个圆柱,尝试从点A到点B沿圆柱侧面画出几条路线,你觉得哪条路线最短呢
A
B
A’
A
B
B
A
C
通过比较、绘图或者测量等方式判断最短爬行方案。
问题2:如图,将圆柱侧面剪开展成一个长方形,从点A到点B的最短路线是什么 你画对了吗
是一条线段
问题3:蚂蚁从点A出发,想吃到点B处的食物,它沿圆柱侧面爬行的最短路程是多少
比较下面几条路的走法:
(1)A→A'→B; (2)A→B'→B; (3)A→C→B; (4)A→B.
(4)A→B.
总结
确定圆柱上的最短路线:
求圆柱上两点之间的最短距离,可转化为求一个平面图形上对应线段的长.
其一般步骤:
(1)将圆柱的侧面展开为一个长方形;
(2)确定相应点的位置;
(3)连接相应点,构造直角三角形;
(4)利用勾股定理求解.
典例精析
例1如图,一只蜗牛从圆柱的点A出法,绕圆柱侧面沿最短路线爬行到了BC的中点E处,若沿AD将圆柱侧面剪开并展开,所得侧面展开图示意图的是( )
C
A. B.
C. D.
即时测评
1.直四棱柱的上下底面是正方形,底面边长为5,高AB为9.在其侧面从点A开始,绕侧面两周,嵌入装饰彩条至点B停止,则彩条的最短长度为( )
A.41 B.50 C.9 D.29
A
2.如图,正方体的棱长为2cm,A是正方体的一个顶点,B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径是 cm.
3.如图,一只蚂蚁从点A沿圆柱表面爬到点B,圆柱高为15cm,底面半径为,蚂蚁爬行的最短路线长为多少?
解:展开之后如图,此时AB的长度即为最短路线长,
此时AC=×2π×=8(cm),BC=15cm,
∴AB===17(cm),
答:蚂蚁爬行的最短路线长为17cm.
装修工人李叔叔想要检测某块装修用砖的边AD和边BC是否分别垂直于底边AB。
该怎么测呢
[任务二 探究勾股定理逆定理的应用]
活动2:
问题1:如果例叔叔只带了卷尺,那么你能替他想办法完成任务吗
利用勾股定理的逆定理,分别量出AB、BC、AC 、AD的长.如果AB2+BC2=AC2,AB2+AD2=BD2,可得AD和BC分别垂直于底边AB.
问题2:李叔叔量得边AD长是30 cm,边AB长是40 cm,点B,D之间的距离是50 cm.边AD垂直于边AB吗
因为AD2+AB2=302+402=502= BD2,所以△ABD是直角三角形,
所以∠DAB = 90°,即 AD 边垂直于 AB 边.
问题3:如果李叔叔随身只有一个长度为20 cm的刻度尺,那么他能检验边AD是否垂直于边AB吗
例如:在AD 上取点 M,使 AM = 9 cm,在 AB 上取点 N 使 AN = 12 cm,测量MN 是否为 15 cm,若是,就垂直;若不是,就不垂直.
例2图①是某品牌婴儿车,图②是其部分结构示意图.根据安全标准需满足AB⊥BC,现量得AB=60cm,BC=45cm,AC=75cm,请通过计算说明该车是否符合安全标准.
典例精析
解:该车符合安全标准,理由如下:
∵AB=60,BC=45,AC=75,
∴
∵=5625,
∴,
∴△ABC是直角三角形,且∠ACB=90°,
∴AB⊥BC,
∴该车符合安全标准.
即时测评
1.如图,甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B.若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向是 .
北偏西60°
2.如图,某小区有一块四边形空地ABCD,连AC,经过测量可得△ABC是等腰三角形,AB=AC=15m,BC=18m,CD=8m,AD=17m.
(1)判断△ACD的形状;
(2)求这块空地的面积.
解:(1)∵AC=15,CD=8,AD=17,
∴
=289,
∴,
∴△ACD是直角三角形,∠ACD=90°;
(2)过点A作AH⊥BC于H,
∵AB=AC=15m,BC=18m,
∴BH=CH=9m,
在Rt△ABH中,AH===12m.
∴S△ABC+S△ACD=BC AH+AC CD
=×18×12+×15×8
=168().
答:这块空地的面积为168.
1.如图,一只蚂蚁从棱长为1的正方体纸箱的A点沿纸箱表面爬到B点,那么它所爬行的最短路线的长是( )
A. B. C. D.2
2.如图,已知圆柱底面的周长为12cm,圆柱高为8cm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为 .
C
20cm
3.如图所示,地面上铺了一块长方形地毯ABCD,因使用时间长而变形,中间形成一个半圆柱的凸起,半圆柱的底面直径为,已知AE+BF=20m,BC=10m,一只蚂蚁从A点爬到C点,且必须翻过半圆柱凸起,则它至少要走 m的路程.
26
4.如图一个三级台阶,它的每一级的长宽高分别是5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,点A上有一只蚂蚁,想到点B去吃可口的食物,则蚂蚁沿着台阶面爬到点B的最短路程长是多少?
解:如图所示,
∵三级台阶平面展开图为长方形,宽为5cm,
长为(3+1)×3=12(cm),
∴蚂蚁沿台阶面爬行到B点最短路程是AB的长,
由勾股定理得AB==13(cm),
答:蚂蚁沿着台阶面爬到B点最短路程是13cm.
5.某村有如图所示的一笔直公路AB,水源C处与公路之间有小片沼泽地,为方便公路上的人用水,拟从C处铺设水管到公路上.已知AB=200米,AC=160米,BC=120米.
(1)求∠ACB的大小;
(2)求铺设水管的最小长度.
解:(1)在△ABC中,AB=200米,AC=160米,BC=120米,
∵==40000,
∴,∴△ABC是直角三角形,
∴∠ACB=90°;
(2)当CD⊥AB时,铺设水管的长度最小,
∵△ABC的面积AB CD=AC BC,
∴AB CD=AC BC,∴200CD=120×160,
解得:CD=96,
∴铺设水管的最小长度为96米.
能说说运用勾股定理的知识可以解决实际生活中哪些问题
课堂小结:
基础题:1.课后练习第 1题
提高题:2.请学有余力的同学做课后习题第3题,并在下节课在班内展示、交流。
课后作业
本节课到此结束,
谢谢大家!
