4.1 无理数(共27张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 4.1 无理数(共27张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 864.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 10:46:11 | ||
图片预览







文档简介
(共27张PPT)
1 无理数
第四章 实数
古希腊有一个毕达哥拉斯学派,他们是数学界的权威,在当时他们提出了这样一个理论:万物皆是数,也就是说宇宙间的一切现象都归结为整数或者整数比。
这个理论在全世界都受到了推崇,但这个学派有一名叫希勃索斯的弟子,他在公元前500年,发现了这么一个事实,边长为1的正方形的对角线长既不是整数也不是整数比 设问:那究竟是什么数呢?
[任务一 探究不是有理数的数]
活动1: 请大家先准备两个边长为1的小正方形,剪一剪、拼一拼,设法得到一个大的正方形.
1
1
1
学生可能出现的拼图结果:
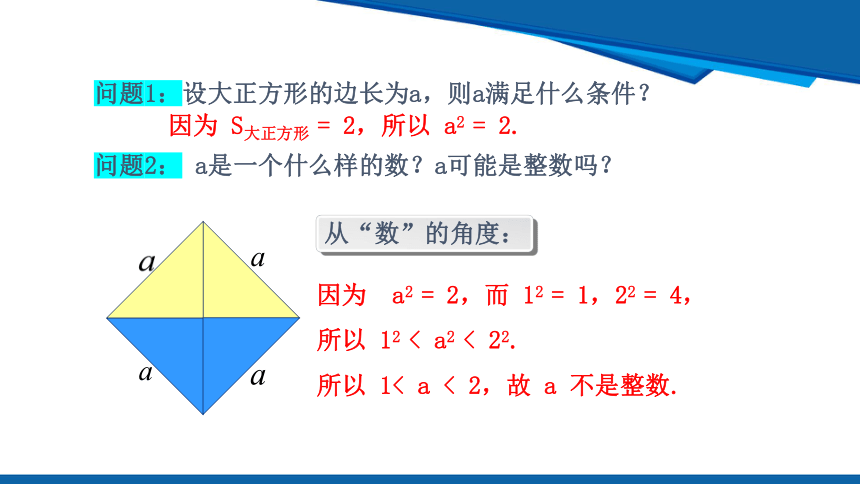
问题1:设大正方形的边长为a,则a满足什么条件?
问题2: a是一个什么样的数?a可能是整数吗?
因为 S大正方形 = 2,所以 a2 = 2.
从“数”的角度:
因为 a2 = 2,而 12 = 1,22 = 4,
所以 12 < a2 < 22.
所以 1< a < 2,故 a 不是整数.
B
A
C
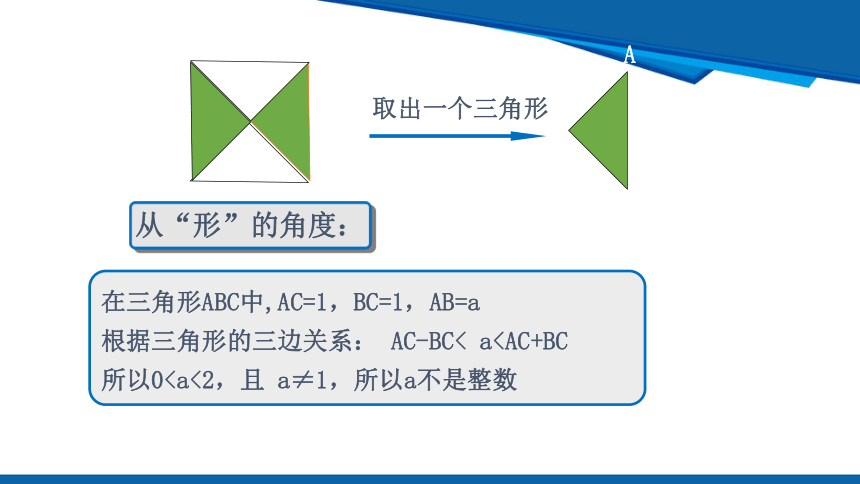
取出一个三角形
从“形”的角度:
在三角形ABC中,AC=1,BC=1,AB=a
根据三角形的三边关系: AC-BC< a所以0问题3: a 可能是分数吗?说说你的理由,并与同伴进行交流.
① a 是分母为 2 的分数吗?
② a 是分母为 3 的分数吗?
③ a 是分母为 4 的分数吗?
④ a 是分母为多少的分数?
a2 = 2
总结:a既不是整数,也不是分数,所以a不是有理数.
例1如图:(1)以直角三角形的斜边为边的正方形的面积是多少?(小正方形边长为1,中正方形边长为2)
(2)设该正方形的边长为b,b满足什么条件?
(3)b是有理数吗?
解:(1)以直角三角形的斜边为边的正方形的面积为+=5;
(2)根据三角形的三边关系可得:1<b<3;
(3)b不是有理数.
典例精讲
即时测评
1.如图,等边三角形的边长为2,高为h,h可能是整数吗?可能是分数吗?是有理数吗?
解:因为三角形是等边三角形,且AD⊥BC,
所以BD=DC,则BD=AB=1,
根据勾股定理得:3,
h不可能是整数;h也不可能是分数,也不是有理数.
问题1:如图,三个正方形的边长之间有怎样的大小关系?
问题2:a的整数部分是几?十分位是几?百分位呢?千分位呢?
1
a
2
面积为2
活动2:面积为2的正方形的边长a究竟是多少呢?
[任务二 探究无理数的概念]
1<a<2
边长a的整数部分是1,十分位是4,百分位是1,千分位是4.
问题3:请同学们借助计算器进行探索
11.961.988 11.999 3961.999 961 64还可以继续算下去吗 a可能是有限小数吗
a=1.414 213 56…, 它不可能是一个有限小数.
问题4:估计面积为5的正方形的边长b的值是多少?b可能是有限小数吗?与同学进行交流.
b=2.236067977···,不可能是有限小数.
活动3
把下列各数表示成小数,你发现了什么?
3,
= 0.8
= 0.5
·
= 0.18
· ·
=﹣0.17
·
有理数总可以用有限小数或无限循环小数表示.反过来,任何有限小数或无限循环小数也都是有理数.
3 = 3.0
无限不循环小数为无理数.如π=3.14159265…,
例2下列各数中,哪些是有理数 哪些是无理数
3.14,﹣,0.,0.101 000 100 000 1…(相邻两个1之间0的个数逐次加2).
解:有理数有:3.14,﹣,0.;
无理数有:0.101 000 100 000 1…(相邻两个1之间0的个数逐次加2).
典例精讲
即时测评
1.在下列数:﹣2.5,,0,﹣1.121121112…,,﹣π中,无理数有( )
A.1个 B.2个 C.3个 D.4个
2.在数﹣65,,3.14,0,,﹣π,0.020020002…中,无理数共有 个.
3.如图,△ABC中,∠C=90°,BC=4,AC=3,
点P在线段AC上,若BP的长度是个无理数,则BP的
长度可以是 .(写出一个即可)
B
2
1.的大小在两个相邻整数之间,这两个整数是( )
A.1和2 B.2和3 C.3和4 D.4和5
2.下列实数是无理数的是( )
A.﹣2025 B.π C.3.14159 D.
C
B
3.以下各正方形的边长是无理数的是( )
A.面积为25的正方形; B.面积为 的正方形;C.面积为8的正方形; D.面积为1.44的正方形.
C
4.下列各数中:12,,,﹣|﹣1|,0.1010010001…(每两个1之间的0依次加1),其中,无理数有 个.
2
5. 已知直角三角形的两直角边长分别是9 cm和5 cm,斜边长是x cm.
(1)估计x在哪两个连续整数之间;
解:根据题意,可得x2=92+52=106.
因为100<x2<121,
所以10<x<11,即x在整数10与11之间.
(2)如果把x的结果精确到0.1,估计x的值;如果精确到 0.01 呢?
解:因为10.12=102.01,10.22=104.04,10.32=106.09,
所以10.22<106<10.32.
因为106-104.04=1.96,106.09-106=0.09,0.09<1.96,所以当x精确到0.1时,x≈10.3.
又因为10.292=105.884 1,10.302=106.09,
所以10.292<106<10.302.
因为106-105.884 1=0.115 9,0.09<0.115 9,
所以当x精确到0.01时,x≈10.30.
本课小结:
4.数的分类.
3.判定一个数是无理数还是有理数.
我们知道整数不够用就产生了分数,正数不够用就产生了负数,现在有理数不够用了,就要产生一种新数——无理数
1.在生活中确实存在既不是整数也不是分数的数,
既不是有理数的数。
2.无理数在现实生活中是大量存在的。
1.无理数是无限不循环小数,有理数是有限小数或
无限循环小数.
2.任何一个有理数都可以化成分数 形式( p,q 为整数且互质),而无理数不能.
强 调
基础题:1.课后习题第 1、2题
提高题:2.请学有余力的同学做课后习题第5题,下节课为全班交流。
课后作业
本节课到此结束,谢谢大家!
1 无理数
第四章 实数
古希腊有一个毕达哥拉斯学派,他们是数学界的权威,在当时他们提出了这样一个理论:万物皆是数,也就是说宇宙间的一切现象都归结为整数或者整数比。
这个理论在全世界都受到了推崇,但这个学派有一名叫希勃索斯的弟子,他在公元前500年,发现了这么一个事实,边长为1的正方形的对角线长既不是整数也不是整数比 设问:那究竟是什么数呢?
[任务一 探究不是有理数的数]
活动1: 请大家先准备两个边长为1的小正方形,剪一剪、拼一拼,设法得到一个大的正方形.
1
1
1
学生可能出现的拼图结果:
问题1:设大正方形的边长为a,则a满足什么条件?
问题2: a是一个什么样的数?a可能是整数吗?
因为 S大正方形 = 2,所以 a2 = 2.
从“数”的角度:
因为 a2 = 2,而 12 = 1,22 = 4,
所以 12 < a2 < 22.
所以 1< a < 2,故 a 不是整数.
B
A
C
取出一个三角形
从“形”的角度:
在三角形ABC中,AC=1,BC=1,AB=a
根据三角形的三边关系: AC-BC< a
① a 是分母为 2 的分数吗?
② a 是分母为 3 的分数吗?
③ a 是分母为 4 的分数吗?
④ a 是分母为多少的分数?
a2 = 2
总结:a既不是整数,也不是分数,所以a不是有理数.
例1如图:(1)以直角三角形的斜边为边的正方形的面积是多少?(小正方形边长为1,中正方形边长为2)
(2)设该正方形的边长为b,b满足什么条件?
(3)b是有理数吗?
解:(1)以直角三角形的斜边为边的正方形的面积为+=5;
(2)根据三角形的三边关系可得:1<b<3;
(3)b不是有理数.
典例精讲
即时测评
1.如图,等边三角形的边长为2,高为h,h可能是整数吗?可能是分数吗?是有理数吗?
解:因为三角形是等边三角形,且AD⊥BC,
所以BD=DC,则BD=AB=1,
根据勾股定理得:3,
h不可能是整数;h也不可能是分数,也不是有理数.
问题1:如图,三个正方形的边长之间有怎样的大小关系?
问题2:a的整数部分是几?十分位是几?百分位呢?千分位呢?
1
a
2
面积为2
活动2:面积为2的正方形的边长a究竟是多少呢?
[任务二 探究无理数的概念]
1<a<2
边长a的整数部分是1,十分位是4,百分位是1,千分位是4.
问题3:请同学们借助计算器进行探索
1
a=1.414 213 56…, 它不可能是一个有限小数.
问题4:估计面积为5的正方形的边长b的值是多少?b可能是有限小数吗?与同学进行交流.
b=2.236067977···,不可能是有限小数.
活动3
把下列各数表示成小数,你发现了什么?
3,
= 0.8
= 0.5
·
= 0.18
· ·
=﹣0.17
·
有理数总可以用有限小数或无限循环小数表示.反过来,任何有限小数或无限循环小数也都是有理数.
3 = 3.0
无限不循环小数为无理数.如π=3.14159265…,
例2下列各数中,哪些是有理数 哪些是无理数
3.14,﹣,0.,0.101 000 100 000 1…(相邻两个1之间0的个数逐次加2).
解:有理数有:3.14,﹣,0.;
无理数有:0.101 000 100 000 1…(相邻两个1之间0的个数逐次加2).
典例精讲
即时测评
1.在下列数:﹣2.5,,0,﹣1.121121112…,,﹣π中,无理数有( )
A.1个 B.2个 C.3个 D.4个
2.在数﹣65,,3.14,0,,﹣π,0.020020002…中,无理数共有 个.
3.如图,△ABC中,∠C=90°,BC=4,AC=3,
点P在线段AC上,若BP的长度是个无理数,则BP的
长度可以是 .(写出一个即可)
B
2
1.的大小在两个相邻整数之间,这两个整数是( )
A.1和2 B.2和3 C.3和4 D.4和5
2.下列实数是无理数的是( )
A.﹣2025 B.π C.3.14159 D.
C
B
3.以下各正方形的边长是无理数的是( )
A.面积为25的正方形; B.面积为 的正方形;C.面积为8的正方形; D.面积为1.44的正方形.
C
4.下列各数中:12,,,﹣|﹣1|,0.1010010001…(每两个1之间的0依次加1),其中,无理数有 个.
2
5. 已知直角三角形的两直角边长分别是9 cm和5 cm,斜边长是x cm.
(1)估计x在哪两个连续整数之间;
解:根据题意,可得x2=92+52=106.
因为100<x2<121,
所以10<x<11,即x在整数10与11之间.
(2)如果把x的结果精确到0.1,估计x的值;如果精确到 0.01 呢?
解:因为10.12=102.01,10.22=104.04,10.32=106.09,
所以10.22<106<10.32.
因为106-104.04=1.96,106.09-106=0.09,0.09<1.96,所以当x精确到0.1时,x≈10.3.
又因为10.292=105.884 1,10.302=106.09,
所以10.292<106<10.302.
因为106-105.884 1=0.115 9,0.09<0.115 9,
所以当x精确到0.01时,x≈10.30.
本课小结:
4.数的分类.
3.判定一个数是无理数还是有理数.
我们知道整数不够用就产生了分数,正数不够用就产生了负数,现在有理数不够用了,就要产生一种新数——无理数
1.在生活中确实存在既不是整数也不是分数的数,
既不是有理数的数。
2.无理数在现实生活中是大量存在的。
1.无理数是无限不循环小数,有理数是有限小数或
无限循环小数.
2.任何一个有理数都可以化成分数 形式( p,q 为整数且互质),而无理数不能.
强 调
基础题:1.课后习题第 1、2题
提高题:2.请学有余力的同学做课后习题第5题,下节课为全班交流。
课后作业
本节课到此结束,谢谢大家!
